Некоторые задачи экономико-математического моделирования

Исследование    задач    управления конкретными      социально-экономическими системами (регион, крупное предприятие, коммерческая структура, отрасль и т.п.) предполагает      наличие      специального модельного, математического и компьютерного инструментария.   Подходы,   использующие адекватные экономико-математические модели и современные методы их исследования (см., например, [1,6]), дают возможность найти пути и методы достижения целей, сбалансировать цели и средства их достижения.

Напомним     необходимую     для дальнейшего постановку классической задачи управления для системы с непрерывным временем. Для дифференциальной системы (Lx)(t) ^ x(t) + A(t)x(t) = F(t)u(t) + f (t),  t e [0, T]

требуется найти управление u , переводящее систему из заданного начального состояния x (0) = а в заданное конечное состояние x(T) = в .    Задачам    управления    для обыкновенных дифференциальных систем и систем с запаздыванием посвящена обширная литература (см., например, [2] и приводимый там    библиографический    список).    В экономической динамике возникает более общая задача управления, в которой цель управления задается системой линейных функционалов, а динамика описывается функционально-дифференциальными уравнениями [5].

Сначала мы приводим необходимые сведения    из    теории    функционально дифференциальных уравнений (ФДУ) и формулируем условия разрешимости общей задачи управления. На основе этих результатов предлагаются соотношения для оценки влияния запаздывания в канале управления на величину ресурса управления, необходимого для решения поставленной задачи.

Для систем с дискретным временем рассматривается возможность коррекции противоречивых     задач     динамического планирования     на     основе     подхода, предложенного для статистических моделей акад. И.И.Ереминым.

Пусть D и     B – банаховы пространства и D изоморфно прямому произведению B× Rn .

Уравнение

L x = f                     (1)

с линейным ограниченным оператором L : D ^ B называется линейным абстрактным функционально-дифференциальным уравнением (АФДУ). Теория уравнения (1) систематически изложена в [1,6,7]. Зафиксируем изоморфизм       J = {Л, Y}: B х Rn ^ D и обозначим через J-1 = [3, r ]    обратного оператора. Здесь    Л: B ^ D, Y: Rn ^ D и

• 3 : D ^ B , r : D ^ Rⁿ -      соответствующие

компоненты операторов J и

J { z , а } = Л z + Y a g D, z g B , a g Rⁿ , J ^{- 1} x = { 3 x , rx } g B х Rⁿ , x g D .

Система

3x = z,  rx = a(2)

называется главной краевой задачей. Таким образом, для любого {z, a} g B х Rn x = Λz + Yα(3)

является решением системы (2). Равенство (3) дает представление оператора L :

Lx = L( Лz + Ya) = Qz + Aa, где так называемая главная часть оператора L , - оператор Q: B ^ B и конечномерный оператор A: Rn ^ B определены равенства-ми Q = LΛ и A = LY . В рамках общей теории уравнения (1) оператор Q    предполагается фредгольмовым (представимым в виде суммы компактного и обратимого операторов).

Рассмотрим общую краевую задачу

Lx = f , £x = в             (4)

с    линейным    ограниченным    вектор- функционалом £ = p^,...,^]: D ^ RN. Крае-задача (4) как объект исследования находится в центре внимания общей теории АФДУ. В случае, когда N= n и задача (4) однозначно разрешима для любого    {f, в} g B х Rn, справедливо представление ее решения в виде x = Gf + X в.(5)

Оператор G: B ^ D называется оператором Грина, оператор X: Rn ^ D,- фундаментальным вектором. Пусть главная краевая задача

Lx = f , rx = α(6)

однозначно разрешима. В таком случае, обозначая через G оператор Грина этой задачи, имеем представление x=G f +Xα(7)

общего решения уравнения Lx = f , считая, что α – произвольный элемент пространства Rⁿ . Из представления (7) следует, что однозначная разрешимость задачи (4) эквивалентна однозначной разрешимости алгебраической системы XX a = в - £G_rf. Таким образом, краевая задача однозначно разрешима тогда и только тогда, когда обратима матрица XX .

Рассмотрим абстрактную задачу управления

Lx = Fu + f , rx = a , £x = в ,     (8)

где управление u принадлежит гильбертову пространству H , F : H ^ B - линейный ограниченный оператор, £ = [£^...,£_N] - целевой вектор-функционал, определяющий цель управления: x = β . Приведем здесь теорему о разрешимости задачи (8).

Определим линейный ограниченный функционал A .: H ^ R , i = 1,..., N , равенством A , u = £ i G_rFu . Очевидно, что можно представить этот функционал в виде скалярного произведения: A , u = ^ i ,,u , где i_z g H -элемент, порождающий A : H ^ R .

ТЕОРЕМА 1 ([6]). Задача управления (8) разрешима для любых f g B , aG Rⁿ, в g R ⁿ тогда и только тогда, когда обратима матрица

M = {(i, i } .

И i j Di,j =1,..., N

N

Управление u₀ = ^ Y h ■, i =1

где col ( y ,..., у _N) = M ^-1[ в — G_rf — X a ], решает задачу (8).

В качестве основной реализации пространства D мы будем рассматривать пространство         D =AC - пространство абсолютно      непрерывных      функций

• x : [0, T ] ^ Rⁿ . В этом случае имеем:

x(t ) = J x ( s ) ds + x (0), B = L -пространство суммируемых по Лебегу функций

T z :[0,T] ^ Rn ,|| z ||L =£ ||z(s)||R„ds,

( Л z)(t ) = f z(s ) ds , Y = E , 6 x = x , rx = x (0). ' ' ' J о ' '

Здесь и всюду ниже E – единичная матрица. Изоморфизм между пространством AC и прямым     произведением     L× Rn играет основополагающую    роль    в    теории функционально-дифференциальных уравнений и дает возможность сводить задачи в пространстве AC к задачам в пространстве L . Систематическое изложение теории краевых задач и задач управления в пространстве AC дано в [1].

Рассмотрим функционально-дифференциальную систему

(L )( t ) = f ( t ),   t e [0, T ],            (9)

где L : AC ^ L - линейный ограниченный оператор с главной частью вида

( Qz )( t ) = z ( t ) - [ K(t , s ) z ( s ) ds. J 0

Здесь элементы klj (t, s) ядра K(t, s) измеримы на множестве {(t,s) :0

| klJ (t,s)| < k(t), i, j = 1,...,n, где функция к(-) суммируема на [0, T]. Заметим, что системы вида (9) охватывают многие классы динамических моделей, включая дифференциальные системы с сосредоточенным и/или распределенным запаздыванием и интегро-дифференциальные системы.

Пространство всех решений однородной системы (Lx )( t ) = 0, t e [0, T ], имеет размерность n .

Пусть { x 1 ,..., x_n } - базис в этом пространстве.

t x (t) = X (t )a + j C (t, s) f (s) ds,       (10)

где C ( t , s ) - матрица Коши.

Пусть £ : AC ^ RN - линейный ограниченный вектор-функционал. Имеет место

T

представление

£ x = j Ф ( s ) x ( s ) ds + T x (0)

, где

элементы измеримой N× n- матрицы Φ ограничены в существенном, а Ψ –

N × n - матрица с вещественными элементами. Рассмотрим задачу управления

Lx = Fu + f , x (0) = a , £ x = в .

Здесь F: L2 ^ L - линейный ограниченный оператор, L – пространство суммируемых с квадратом функций u : [0, T] ^ Rr , в котором скалярное произведение     определено

T

Uu , v) = j u ¹ ( t ) v ( t ) dt , где

⊥

⋅ -

транспонирования. В задаче равенством сим-    вол

(11)   цель

управления задается вектор-функционалом

£ : AC ^ R N , который на траектории системы

Lx = Fu + f под действием управления должен принимать заданное значение β . Критерий разрешимости такой задачи управления дает приводимая ниже теорема. Для ее формулировки введем обозначения:

T

0 ( s ) = Ф ( s ) + | ф ( ^ > C ^ ( £ , s ) d ^ ,

s

W = j [ F * 0 ]( s )[ F * 0 ] ¹ ( s ) ds , 0

F * : L * ^ L 2 - оператор, сопряженный к F .

ТЕОРЕМА 2 ([6]). Задача управления (11) разрешима тогда и только тогда, когда линейная алгебраическая система

T

W . Y = в - j 0 ( s ) f ( s ) ds -T- a    (12)

разрешима относительно N - вектора

• Y . Каждое решение / ₀ системы (12) определяет управление, решающее задачу (11):

• 3.    Зависимость    управляющей

u ( t ) = [ F W ( t ) - / 0 .         (13)

программы от запаздывания

Опишем зависимость управления и расходов на него (по норме пространства L ) от запаздывания для случая классической задачи управления (перевод из начального состояния x (0) = 0 в конечное состояние x(T ) = в ), считая запаздывание τ в цепи управления постоянным:

Lx = F u ; x (0) = 0; x(T ) = в ,      (14)

где ( F u )( t ) = F(t )(T u )( t ), (Т мл  Z u ⁽ t^-T), t ^{e [ T} , ^{T ]},

^{( T u )(} t ) = i _{n ( m} ,

I 0, t e [0, т ].

Для задачи (14) матрица 0(s) = C(T, s), и для построения управления (13) остается найти сопряженныи оператор F : L ^ L2.

Используя равенство

_ х ( 1 Отсюда C (3, s ) =

I 0

J ( s ) ] e^{s — 3} J ,

т получаем

J z ¹ ( t ) F ( t ) и ( t — т ) dt = J x _[0> t _ , ] ( s )[ z ¹ ( s + т ) F ( s + т )] и ( s ) ds ,

W ( т ) = ² Г f   J ²⁽ s + ^{т )}

{ ^ J ( s + т ) e^{s + т}

J(s + т)es+т—3 [ , 2     2       ds + e 2( s+т -3)      I

^{( F} *^{z )(} s ) = X [0, Tт ⁽ s ) ^{F 1 (} s ^{+ т ) z (} s ^{+ т )}.

Отсюда для «матрицы управления»

3— т

+J

2 —т

к , ds — 0 e ^{2( s + т} " ³⁾ J

W = W ( т ) имеем представление	f 3 — т + 2 e — 2 — 1 e "'— 2)	1 e -1 +1 e 2т 5"
T	2            2	2     2
W = J Z p, T т] ( s ) C (T , s + т ) F ( s + т ) F 1 ( s + т )С 1 ( T , s + т ) ds =     = 0	1     1 + 1 ^2 т —5 — e + — e	1[1 — e2(r — 3)]
T —т	I     2     2	2            J

,

= J C(T , s + т )F ( s + т )F ¹ ( s + т ) C ¹ (T , s + т )ds • 0

Таким

разрешима для det W( т ) ^ 0 .

образом, всех таких

Управляющая

задача (14)

т е [0, T ] ,   что

программа

определяется равенством (13):

J F ¹ ( t + т ) C ¹ ( T , t + т ) W -1 ( т ) Д , t е [0, T — т ]; U (t ) = 1

^т      I                 0, t е ( T — т , T ].

«Расходы на управление» S ( т ), как функцию

параметра т , оцениваемые по норме

пространства L , можно вычислить:

S ( т ) = | Ы1 4 J и 1 ( t ) и т ( t ) dt I

•

Очевидно, характер этой зависимости определяется конкретными особенностями системы управления - матрицей Коши C ( t , s ), матрицей F ( t ) и целевыми значениями компонент требуемого финального состояния в .

Рассмотрим систему управления с запаздыванием по состоянию и по управлению

X ( t ) = x ₂ ( t — 1);

x ₂( t ) = — x ₂( t ) + и ( t — т ),    t е [0,3];

X 1 (0) = 0; x 2 (0) = 0; X 1 (3) = Д ; x 2 (3) = Д 2 ;

x ₂ ( £ ) = 0, и ( £ ) = 0, если £ <  0.

Для этого случая имеем F(t ) = col (0,1),

r = 1, матрица Коши определяется равенством [7]

t'                                                   3

J Z [1,3j ^{( £} ) Z _[0^ —1] ⁽ s ) ^exP^{(1 —} - ⁺ s ) ^{d £}

•

s exp( s — t)             j

C ( t , s ) =

Вычисляя интеграл, определяющий элемент c2 (t, s) , для J(s) = c2 (3, s) получаем

1 — e^{s — 2}, s е [0,2],

0, s е (2,3].

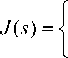
и т ( t ) = (0,1) 1

[ J ( t + т )

e

0 3   , Г Д

, W ( т )

^{+ т} — ³ J        I в

•

Приведем точное описание S ²( т ) для

Д = ^2 = 4:

S ²( т ) = 18( — 10 + 14 т — 20 тe^{2 т — 6} + 6 e ^{— 2} — 4 e^{4 т — 10} — 3 e^{4 т — 1}

—

— 28 в ^{т — 2} — 9 e ' ^: — ⁴ + 2 e ^{- l} + 16 e^2т — ⁵ + 6 e^{2т — 6} + 4 в ^т — ⁵ — 4 e -‘т —

— 22 e ^{4 т — 11}

+ 8 т е ^{3 т — 9}

—

2 e -³ — 2 e^{4 т — 9} + 8 т e ^{т — 4} — e^{2 т — 8}

— e^{4т 8} + 16 e ² т + 4 e^:

—

4 e ^{2 т — 4} т + 4 e ^{3 т} — ¹⁰ +

— 4 т ² + 20 e ^{т — 3} + 8 e ³

—

— 8 e ^! — ³ т — 12 e ^! — ⁴ + 2 e^{4 т} — ¹² т + 2 e^{4 г — 10} т + 4 e ^{2 т — 7} т + 4 e ^{4 т —}" т

—

— 4 e^{2 т — 5} т — 12 e ^{3 т — 9} — 8 e^{2 т — 7} + 28 e ^{3 т — 8} + 4 т² e ^{2 т — 6} — 2 e ~²т —

— 8 т e ^{3 т — 8})/( — 9 + 12 т — 32 т e^{2 т — 6} + 6 e "² + 22 e ^{4 т — 10}

— 24 e ^{т — 2} — 10 e ^{2 т — 4} + 28 e^{2т — 6} — e ^{— 4} — 10 e ^{2 т — 8}

— 4 e ^{2 т — 4} т — 8 e^{З г — 10}

—

16 e^{6т — 16}

—

e^4т - ⁸

—

—

25 e ^{4 т — 12}

—

—

4 т² e^{4т — 12}

—

40 e ^{5 т — 14} + 16 e ^{т — 2} т

—

■4 т ² + 8 e ^{3 т — 6} + 8 e ^{r — 4} + 20 e ^{4 т} ^г + 4 e^{, т — |0} т + 4 т в ^{2 т — 8} +

+ 64 e^{З т — 8} + 16 тe^{5 т — 14} + 8 т² e^{2 т — 6} — 4 e ^{— 2} т — 8 e^{5 т — 12} — 32 тe^{З т — 8})

Вид зависимости S ( т ) представлен на рис. 1.

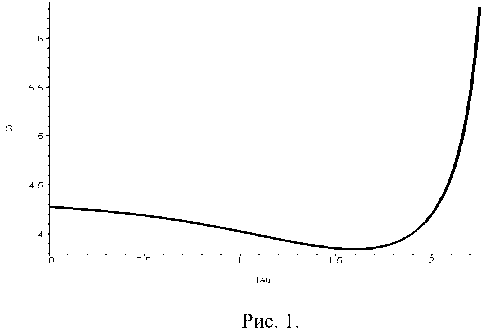
Заметим, что в точке т ₀ е [2,390; 2,391] det W ( т ) = 0 и задача управления решения не имеет.

При экономико-математическом моделиро-вании динамические модели с дискретным временем часто возникают как

результат эконометрического моделирования на базе реальной статистической информации.

Рассмотрим неавтономную систему x (t +1) = ^ A(t, i) x (i) + f (t +1), t = 0,..., T -1, i=0

(15) где x(t ) g Rⁿ, t = 0,..., T , A ( t , i ) - n x n - матрицы.

Данная система, дополненная начальными условиями x (0) = a , имеет единственное решение. В частном случае A(t , i ) = A (i ) V t коэффициенты системы (15) могут быть результатом стандартных процедур эконометрического моделирования.

В составе экономико-математической модели система (15) учитывает лишь динамические связи переменных, не включая в себя статические ограничения, такие, например, как балансовые ограничения.

Добавление в модель даже линейных статических ограничений вида

Bx <  d , (16) где B - матрица размерности m x nT , d -вектор-столбец размерности m , а x = col ( x^T ( 0 ) , x^T ( 1 ) ,..., x^T ( T ) ) , может привести к тому, что система (15)-(16) окажется несовместной.

В этом случае возникает задача коррекции построенной модели. Систематическая теория таких задач изложена в [3,4]. Одной из причин корректировки может служить тот факт, что коэффициентами системы (15), построенной в результате эконометрического моделирования, являются не точные фактические коэффициенты, а их оценки, полученные по статистической информации. Поэтому задачу коррекции можно поставить в форме отыскания таких поправок h к данным коэффициентам, которые приведут к совместности системы (15)–(16) в целом. При этом имеет смысл следить за тем, чтобы измененные коэффициенты попали в доверительные интервалы, построенные для фактических значений коэффициентов модели по исходным оценкам.

Коррекцию ограничений (16) можно проводить также в виде введения штрафа за их нарушение.

Приведем систему (15) к виду, удобному для коррекции, – запишем ее в виде:

x = Px + F , (17)

где

P =

E n

A ( 0,0 )

A ( 1,0 )

A ( 1,1 )      0

1 A ( T - 1,0 )   A ( T - 1,1 )

0        0

A (T -1, T -1)  0

F = col 0,...,0, f^T ( 1 ) ,..., f^T ( T )

I

Введя обозначение

K = ( E nT +»" P ) =

' En - En         0       0         00 '

- A (0,0)       En       0         00

=   - A (1,0)      - A (1,1)    En         00

_cA ( T - 1,0 )   - A ( T - 1,1 )       - A ( T - 1, T - 1 )

запишем (17) в виде

Kx = F.

В результате приходим к системе (18),(16), для которой в качестве коррекции может быть применен метод параметризации, разработанный      И.И. Ереминым      и

А.А. Ватолиным [3,4]. Параметризованная система, соответствующая системе (18),(16), запишется в следующем виде:

'( K + H , ) x = F - p ,

( B + H ₂) x <  d - p₂

где H. = hiA    ,

1   № ) nT,nT p1 = col (hj,nT-1, • • • , hnT,nT+1 ) ,

Hl ={ h J , j = nT + 1,..., nT + m, i = 1,..., nT ,

P 2 = co^l ( h nT + 1, nT + 1 , • • • , ^h nT + m , nT + 1 ) .

Количество параметров системы (19) составит ( nT + m )( nT + 1 ) . Так как для системы (16) коэффициенты матрицы B строго определены, коррекцию, как уже говорилось выше, можно проводить лишь в форме штрафов за отклонения от выполнения ограничений, т.е.

корректируя параметры р ₂, при этом матрица

H будет нулевой. В силу специфического вида матрицы K число параметров будет совпадать с общим числом элементов матриц

A ( t , i ) .

Таким образом, вектор рассматриваемой модели размерность m + -—^— n ².

параметров h будет иметь

Для системы (19) ставится следующая задача аппроксимации:

inf { Ф ( h )| h e M о S } , где S -допустимое множество параметров, M – множество параметров, для которых параметризованная система (19) имеет решение, Ф ( h ) - функция качества аппроксимации. Решение этой задачи дает оптимальный с точки зрения критерия Ф ( h ) вектор коррекции h.