Некоторые задачи теории графов в системе "Mathematica"

In the given work is considered application of computer system " Mathematica " at the decision of combinatory tasks of school mathematics. Introduction of this technique in a school rate considerably raises a learning efficiency to the decision of difficult and toilful tasks of graph theory.

Изучение элементов теории графов в школе представляется целесообразным по нескольким причинам. Прежде всего, теория графов является важной областью современной математики, имеющей широкое практическое применение. В настоящее время такие дисциплины, как физика, химия, экономика, исследование операций, социология, а также многие другие, имеющие важное прикладное значение, широко используют методы дискретной математики и полученные в ней результаты. Эти результаты очень важны, например, при разработке различных технических устройств с дискретным принципом действия, построения машинных алгоритмов, в планировании и радиоэлектронике. Кроме того, рассматриваемый материал является наглядным, отличается богатым, но в то же время вполне доступным для понимания учащихся математическим аппаратом. Сторонники включения в систематический курс математики теории графов и ее приложений [1,2] обращают внимание на доступность, наглядность, и, что немаловажно, широкое применение теории графов к решению задач (арифметических, логических, комбинаторных задач на сравнение числа элементов множеств).

В дискретной математике особое место занимают задачи, связанные с упорядочиванием тех или иных объектов и построением сложных конструкций путем «правильного» соединения отдельных элементов, а также задачи, в которых изучаются отношения между различного рода объектами. Это задачи, решение которых сводится к поиску гамильтонова пути или кратчайшего пути на графах.

Приведем решение нескольких таких задач с использованием компьютерной системы “Mathematica”. Стандартный пакет расширения «DiscreteMath'Combinatorica' этой компьютерной системы обладает богатейшим набором встроенных функций теории графов и комбинаторики (около 450). Он содержит функции для конструирования графов и других комбинаторных объектов, вычисляет их инварианты и, наконец, позволяет создать их графическую визуализацию.

Задача. Три ревнивых мужа и их жены должны переправиться через реку. Имеется только один маленький бот, который может выдержать одновременно только двоих человек. Как могут переправиться все шестеро, если никакой муж не оставит жену в присутствии других мужчин?

Решение. Пусть нужно переправиться с левого берега на правый берег. Сформируем множество 1 всех возможных сочетаний людей на левом берегу, причем, в каждом сочетании последний символ b означает наличие бота у группы оставшихся, а символ о -отсутствие такового.

in{2J:= 1 = {(ml, m2, m3, vl, v2, v3, b}, (ml, m2, m3, vl, b] , {ml, m2, m3, v2, b) , (ml, m2, m3, v3, b] , (ml, m2, vl, v2, b] , (ml, m3, vl, v3, b] , (m2, m3, v2, v3, b), {mi, m2, m3, v2, b} ,

{ml, m2, m3, v3, b}, (ml, m2, m3, v2, v3, b}, (ml, m2, m3, vl, v3, b], (ml, m2, m3, vl, v2, b},

(nil, vl, b} , (m2, v2, b), (m3, v3, b), {vl, v2, v3, b}, (vl, v2, b) , (vl, v3, b), (v2, v3, bl , (ай, m2, m3, vl, o} , (ml, m2, m3, v2, o}, {ml, m2, m3, v3, o), {ml, m2, vl, v2, o),

(ml, m3, vl, v3, o] , (m2, m3, v2, v3, o) , {ml, m2, m3, v2, o} , (ml, m2, m3, v3, o) , (ml, m2, m3, o) ,

(ml, vl, o}, (m2, v2, o), {m3, v3, of, {vl, v2, of, {vl, v3, o), [v2, v3, o), (vl, o) , (v2, o) , (v3, o), (o});

Этот список содержит 38 элементов.

ад = Length[l] ■

ОШ[3]= 38

Построим бинарное отношение на множестве 1:

1п(4]:= кг = tbdule[(t = Cooplement[#l, #2]},

Length[#2] -Length[#l] «1661ast[#l; =!= Last[#2) 68Last[#l] = оЫLength[#2] = !=7« Iengtii[Cc«pleirent[#2, #1]] == 2 || Length[#2] -Length[#l] == 2 8S Last[#l] =1= Last[#2] S& Last[#i];: oMLength[#2] = !=7 86Length[Ccaplerent[#2, #1]] == 3 11

{Lengtii£#l] - Length [ #2] ^- 2 88 Last[#l] ='= Last[#2] «Length[Complement^ #2]J = 3S8iast[#l] ==b)] 4;

Построим граф с вершинами в точках множества 1, причем две вершины связаны ребром, если они удовлетворяют отношению кг: lr^5|- ShowLabeledSr^>h[g= №JceGraph[l, кг], EdgeDirection-» True)

Рассмотрим кратчайший путь из первой вершины в тридцать восьмую:

ад - ShortestPath[g, 1, 38]

ОИ№ (1, 21, 10, 28, 2, 29, 5, 32, 16, 35, 13, 38)

Рассмотрим исходные метки соответствующих вершин, именно они показывают искомое решение задачи:                                                                       .

ад:= №р[1[[#]] &, ShortestPath[g, 1, 38]] Ш[7]= {{ml, m2, m3, vl, v2, v3, bj, {ml, m2, m3, v2, o}, [ml, m2, m3, v2, v3, b), {ml, m2, m3, o], {ml, m2, m3, vl, b}, {ml, vl, o), {ml, m2, vl, v2, b), {vl, v2, o}, [vl, v2, v3, b), [vl, o], [ml, vl, b], (o)}

Выделим кратчайший путь от первой до тридцать восьмой вершины:

ад - ShowLabeledGraph[Highli^it[g, (Partition[ShortestBath[g, 1, 38], 2, 1]}]]

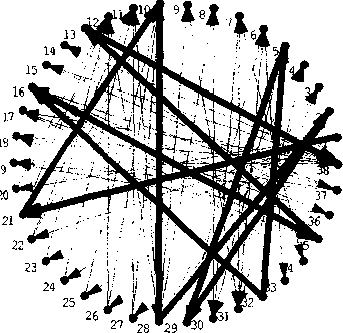
Улучшим вложение графа с помощью встроенной функции RankedEmbedding: lrt9J = ShowGraph[RankedEhbedding[g, {1}], EdgeDirection-* True]

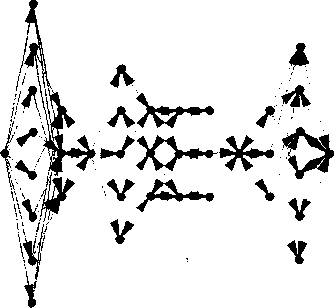
Выделим гамильтонов цикл:      - inflOj- ShcwGraph[Highlight[RankedEtibedding[gr (!}], (Partition]ShortestPath[g, 1, 39], 2, 1]}]]

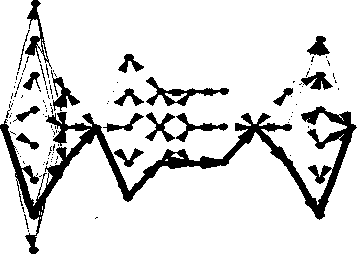
Задача. Требуется перечислить все перестановки множества {1,2,...,п} в таком порядке, чтобы каждая последующая перестановка отличалась от предыдущей ровно одной транспозицией.

Решение. Достаточно свести задачу к нахождению гамильтонова пути на графе.

На множестве всех перестановок определим бинарное отношение Р: две перестановки находятся в отношении Р, если они отличаются друг от друга ровно одной транспозицией. Как известно, бинарное отношение можно представить графом, вершины которого соответствуют элементам множества, и две вершины смежны, если они находятся в данном отношении.

Заметим, что две перестановки находятся в отношении Р, если они отличаются как упорядоченные множества ровно в двух позициях. Следующая функция определяет Р:

fn[25j- Р = (р- #l;q = #2; к = 0; Do[If[p[[i]] »q[[i]], , к = к+1], [i, 1, Length]#!])] ?

If[k==2, True, False])

Мы определили функцию P от двух аргументов, здесь р=#1 -первая перестановка, q=#2- вторая перестановка, далее в цикле Do[] подсчитываем количество к несовпадающих позиций в этих перестановках. Функция возвращает True, если к-2. Рассмотрим пример для перестановок длины 4.

h427i:= g= №dceGr$Th[Penmitations[4] , Р, Type-* Undirected]

0^(27]= -Graph:<72, 24, Undirected:--

Для наглядности построим ранжированное вложение вершин этого графа относительно первой вершины:

ln(2S3 = ShowGraph; RankedEobeddingi'g, (!}]]

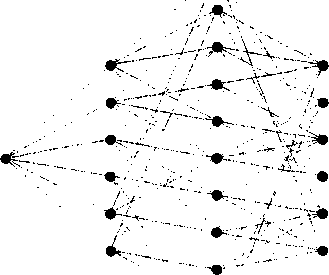
Если мы хотим определить перестановку, соответствующую каждой вершине графа g , то достаточно в теле графа установить опцию Vertex Label->True, но метки сильно загромождают рисунок.

In[29]- h= Make<3ra$4i[ Permutations [4], Р, Type-* Undirected, VertexLabel ->True] ;

ShcMGraph[RankedEmbedding[h, (1)]]

_ 4321

#А213

* 4132

_.34Й -

3214 -

3241 \

2134 ■

Д234 ■ ■

1432 -

'    /.1324

. 2431

1243,

■     2314

:' 2341

214»

’ ^Т342

Проверим, является ли граф g гамильтоновым:

!n(30] = HamiltonianCycle[g]

Cut£30]= (1/ 2, 4, 3, 5, 6, 12, 7, 8, 10, 9, 11, 17, 14, 13, 15, 16, 18, 24, 19, 20, 23, 21, 22, 1)

Выделим этот гамильтонов цикл в графе:

!^31]r ShovKSraph; RanJcedErrbeddingг Highlight {g, {Partition; HanhltonianCycle{g], 2, 1]}], {!}]]

Пройдя по вершинам этого гамильтонова цикла, получим все перестановки размера 4, причем любые две смежные перестановки отличаются ровно одной транспозицией.

1пГ32р= GetVerterLabels[h, HamiltoniariCyaLefh] ]

Ол[3^= (1234, 1243, 1342, 1324, 1423, 1432, 2431, 2134, 2143, 2341, 2314,

2413, 3412, 3142, 3124, 3214, 3241, 3421, 4321, 4123, 4132, 4312, 4213, 4231, 1234}

Построим расстояния в графе от первой вершины:

1л(34];= RankGraph[g, (1)]

Out(34]= {1, 2, 2, 3, 3, 2, 2, 3, 3, 4, 4, 3, 3, 4, 2, 3, 3, 4, 4, 3, 3, 2, 4, 3}

Рассмотрим распределение расстояний:

1л(35}:= Distribution[RankGraph[g, {1}]]

СМ[35|= {1, 6, 11, 6}

Отсюда следует, что шесть перестановок можно получить из тождественной перестановки одной транспозицией, одиннадцать перестановок - двумя транспозициями и шесть -тремя транспозициями.

То же самое можно вычислить с помощью числа Стирлинга первого рода:          - fn[36j:= Table[StirlingFirst[4, i], {i, 4, 1, -1}]

Out{36p (1, 6, 11, 6]                                     .

В предыдущей задаче перестановки перечислялись в порядке минимального отличия друг от друга. Поставим обратную задачу:

Требуется перебрать все перестановки множества {1,2,...,п} в таком порядке, чтобы каждая последующая перестановка отличалась от предыдущей во всех позициях.

Известно, что перестановки Я[ и л? отличаются друг от друга во всех позициях, если произведение (д?)'1*^ есть перестановка без неподвижных точек.

Построим булеву функцию и граф, вершинами которого являются перестановки размера 4, а две вершины смежны, если соответствующие им перестановки отличаются во всех позициях:

inf39}; = d = DerangementQ [ Permute [ inversePennutation £ #1], #2]]

dgraph = MakeGraph[Permutations[4], d. Type-* Undirected, VertexLabel -> True]

Cut№ -Graph:<108, 24, Undirected»-

Чтобы метки перестановок сильно не загромождали рисунок, установим опции меток: ln[4i)- h= SetGrafhOptions[dgraph, (1, 8, 10, 11, 14, 17, 18, 19, 23, 24, VertexTabel Position -> Uppetieft

Oulpir -Graph:<108, 24, Undirected^• ln[42]:= ShowGrcph[RankedEntoedding[h, {1}]]

2 ■ 4213

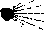
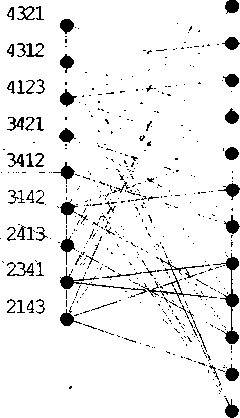
Проверим, будет ли этот граф гамильтоновым:

in[43]- HamiltonianQ[h]

Out[43]= True

Выделим гамильтонов цикл в графе h:

Ц44]~ 1= HamiltonianCyale[dgraph]

Oul[44]= (1, 8, 3, 11, 4, 7, 2, 9, 5, 10, 6, 13, 12, 19, 15, 20, 16, 23, 18, 21, 14, 22, 17, 24, 1}

!Ц45|:= Sho«Graph[ RankedEnbeddingl Highlight [h, {Bartition [ HandltonianCycle [ h], 2, 1]}], {!}]]

2^4

Чтобы последовательность вершин и ребер в гамильтоновом цикле была явно выделена, лучше выделить гамильтонов цикл анимацией. Для этого выделим последовательность вершин и ребер гамильтонова цикла:

ед-- s= (1, (2, 8}, 8, (8, 3}, 3, (3, 11}, 12, (21, 4}, 4, (4, 7) , 7, <7, 2} , 2, (2, 9} ,9, {9, 5}, 5, (5, 1CJ ,

10, (10, 6) , 6, (6, 13} , 13, [13, 12}, 12, [12, 19} , 19, (19, 15}, 15, (15, 20} , 20, (20, 16), 16,

(16, 23) , 23, (23, 18}, 18, <18, 21}, 21, {21, 14), 14, (14, 22}, 22, {22, 17}, 17, <17, 24}, 24, (24, 1}};

♦

Эта команда в динамике покажет прохождение вершин цикла:

№[47]- SniMteGr^h[RankedEiibedding[h, {1}], s]

i 4213

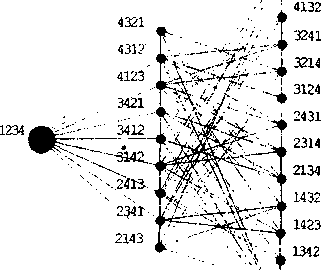
■^ 1243

Дважды кликнув по этому рисунку, можно увидеть прохождение по всем вершинам и ребрам гамильтонова цикла:

Out[48|= (1234, 2143, 1324, 2413, 1342, 2134, 1243, 2314, 1423, 2341, 1432,

3124, 2431, 4123, 3214, 4132, 3241, 4312, 3421, 4213, 3142, 4231, 3412, 4321, 1234}

Эту задачу можно решить с помощью бинарного отношения Q:

№6= {p=81;q = #2;k=0;Do[If[p[[iH =!=q[[ij], , k = k+l], {i, 1, tengtii[#l]}];If[k>0, False, True]) 6;

Или проще:

in[505:= Q= (Count[#l- #2, 0] = 0) &;

Построим граф отношения Q:

1п(511 = ShowGraph[

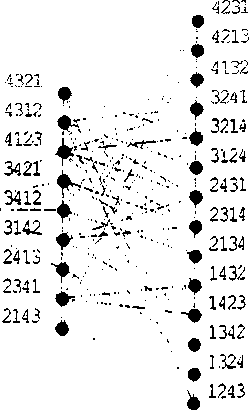
Выведем вершины гамильтонова цикла:

in[52j~ GetVertexLabels[g, HamiltcnianCycle[g] ]

Out[52]= {1234, 2143, 1324, 2413, 1342, 2134, 1243, 2314, 1423, 2341, 1432,

3124, 2431, 4123, 3214, 4132, 3241, 4312, 3421, 4213, 3142, 4231, 3412, 4321, 1234}