Некоторые заметки о решении систем линейных уравнений

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 512.6:519.61                                  

В настоящее время умение применять теоретические знания при решении практических задач становится решающим фактором для изучения любой дисциплины. В частности, исходя из многолетнего опыта преподавания бизнес математики в экономическом вузе, авторам представляется необходимым продемонстрировать решение некоторых экономических задач при помощи математического аппарата [1, 2].

Если мы не сможем улучшить математическое образование, учитывая потребности современного мира и студентов, мы находимся в опасности превращения математики во все более «мертвый язык» и отчуждения групп студентов, математический потенциал которых останется неразвитым [3, 4].

Во многих случаях инвестиционных проектов производства вклады возвращаются одинаковым потоком платежей или другим видом выплат. Его называют «аннуитетом». [5].

Одна из причин введения понятия «деления» матриц заключается в возможности применения метода матриц для решения систем линейных уравнений.

Например, рассмотрим систему уравнений с четырьмя неизвестными:

3 %j + 8 x2 + x3 + 2 x4 = 96

20x - 2x2 + 4x3 + 0.5x4 = 69

11 x + 3x2 + 3x3 - 5x4 = 75

X +12 x2 + x3 + 8 x4 = 134

Эти уравнения можно выразить в матричной форме следующим образом:

• -    постоянные коэффициенты четырех неизвестных x 1 , x 2 , x 3 и x 4 определяют матрицу А размера 4×4;

• -    сами четыре неизвестные задают вектор х размера 4 × 1;

• -    постоянные в правой части уравнений задают вектор b размера 4 × 1.

Систему можно записать следующим образом:

	■ 3	8	1	2 ’	■ x:		"96 ’
Ax =	20 11	- 2 3	4 3	0.5 - 5	x 2 x 3	—	69 75	= b
	_ 1	12	1	8	_ x 4 _		_ 134 _

Правильность этой записи можно легко проверить, воспользовавшись правилом умножения матриц Ax . Элементы строк матрицы A умножаются на соответствующие элементы вектора x и складываются. Если посчитать все элементы произведения Ax и приравнять их к соответствующим элементам матрицы b , получим совместную систему линейных уравнений. Например, перемножение элементов первой строки матрицы A на соответствующие элементы вектора x дает первый элемент произведения Ax

3 x + 8 x ₂ + x ₃ + 2 x₄ .

Приравнивая его к первому элементу 96 вектора b , получим первое уравнение.

x ₁, x ₂,    , x_n

Эту систему уравнений можно решить каким-нибудь стандартным способом, но матричный метод обладает преимуществами, с которыми ознакомимся в следующих разделах. Метод матриц применим и в общем случае. Пусть задана система n линейных уравнений с п неизвестными b 1 , b 2 , b 3 … b n — свободные члены.

a x, + a x, +-----+ ax = b

11 1     12 2            1 nn     1

a₂x + a₂₂x₂ +-----+ a_2nx_n = b 2

a n 1 ^x 1 ⁺ a n 2 ^x 2 +- + a nn x n = bn

Эту систему n линейных уравнений с n неизвестными можно записать в матричном виде Ax = b , здесь A – матрица коэффициентов размера n × n

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №5 2025

A = ~ a11 a 21 a12  ’ ’ a 22 ’ • a1 n ’ " a 2 n X = X1 x b = b1 Ь2 _ an 1 an 2  ’ ■■ ann _ , _ Xn _ - матрица неизвестных, _ bn _ - матрица свободных членов.

Как можно решить эту совместную систему уравнений Ax=b для неизвестных x ? Если бы в уравнении Ax = b A и b были не матрицами, а числами, из этого соотношения неизвестную x легко найти в виде ^x = A ' b . Попытаемся найти решение в этом виде и в случае, когда x, A и b матрицы. Системой т линейных уравнений с n неизвестными называется следующая система:

'an x! + a12 x2 +••• + ajXj +••• + anXn = b(1)

a21 xx + a22X +-----+ a2j xx +-----+ a2nXn = b —    —      —       —     —— ail X1 + ai2 X2 +■■■+ aijXj +■■■ + ain Xn = bi —      —      —       ——

^ am 1 X1   am 2 X2 +--' + amj Xi + ' ' ' + amnXn = bm, a.,b (i = 1,m; j = 1,n )

здесь ij i               ‒ заданные числа, au ‒ коэффициенты перед неизвестными, bi ‒ свободные члены.

A =

^a 11 ^a12 ... ^a 1 n

a 21

a22 • ' • a 2 n

—

—

—

—

^ a mi a m 2 * ’ * a mn у

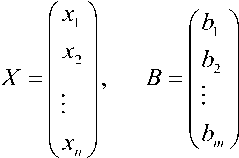
здесь A называется матрицей коэффициентов (1) или матрицей системы, B – матрицей свободных членов. Тогда заданную систему уравнений можно записать в виде: AX = B.

Определение. Если система уравнений имеет решение, она называется совместной, иначе несовместной.

Определение. Если совместная система уравнений имеет единственное (бесконечно много) решение, она называется определенной (неопределенной). Пусть кроме системы уравнений задана следующая система уравнений.

Определение. Если множества решений систем уравнений совпадают, они называются равносильными (эквивалентными).

Решение системы уравнений методом матриц

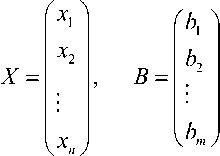
a11 a12 .. . a1 n a21 a22- •• a2 n

- - - -

^ a m 1 a m 2 • * ’ a mn J

З десь A называется матрицей коэффициентов матрицы, B – матрицей свободных членов. Тогда заданную систему уравнений можно записать в виде AX = B.

Пусть в системе уравнений число уравнений равно числу неизвестных, т.е. m = n . В этом случае матрица системы A будет квадратной. Если ^A ^ 0 , т.е. A - невырожденная матрица, существует обратная матрица A^-1 , то из равенства AX = B находим следующее: A ( AX ) = A B ^ ( A A ) X = AB ^ EX = A B ^ X = A B , из этого соотношения:

; 11

f x ¹ x.

I x n J

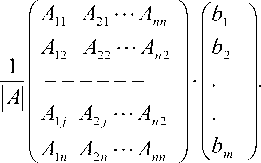
x j = T⁽ b ¹ A ¹ j + b 2 A 2 j

Из последнего равенства вытекает      ^A

+ - + b n A nj ) = ^A j, A j = 1, n A

2 x + 3 x2 + 4 x3 = 1

« Xj + 2 x2 + 3 x3 = 0

Например. Решим систему уравнений

3 X + 4 x ₂ + 6 x₃ = 1

^{1  1    2    3}       методом матриц.

Соответствующие системе основная матрица, матрицы свободных членов и неизвестных

	f 2  3  4 1		f 1 1		f X j i
A =	123	, B =	0	, X =	X 2
будут следующими:	. 3  4  6 J		1 1 J		ч X 3 J

Так как f 0   -21

A-1 =3   0

| A| = 24 + 27 +16 - 24 - 24 -1 = 1 ^ 0        1—2   11

	( 0    - 2   1 1		f 1 1		f 1 1
X = A 1 • B =	3   0   - 2	•	0	=	1
Тогда	X 2   1    1 J		[1 J		[~ 1J

Значит, x 1 = 1, x 2 = 1, x 3 = -1.

Решение системы уравнений по правилу Крамера. Метод Крамера является одним из методов решения систем уравнений, при котором решения легко находятся через детерминанты. Этот метод более эффективен при нахождении одной определенной переменной. Несмотря на то, что в программе Excel можно находить обратную матрицу и перемножать, неважно, сколько времени уходит на вычисления вручную. Поэтому для изучения экономических процессов удобным считается метод Крамера. Для более сложной экономической математики ниже приводится правило Крамера в виде алгебраической формулы. Известна матричная запись системы линейных уравнений с п неизвестными x 1 , x 2 , K, X n Ax = b , здесь A - матрица параметров размера n x n , x - вектор неизвестных размера n x 1 и b – вектор свободных членов размера n × 1.

Метод Крамера означает для нахождения любой неизвестной x i подстановку в i- й столбец матрицы A элементов матрицы b , деление детерминанта полученной матрицы на

Ai xi   A детерминант матрицы A. Значит,

Пример. Найдите неизвестные x 1 и x 2 при помощи правила Крамера

5 x + 0.4 x ₂ = 12

3 x + 3 x ₂ = 21

Ax =

Решение. Матричный вид этой системы

0.4   X 1

Найдем неизвестную x 1 , применив правило Крамера

A 2

x ² A l

Точно также находится неизвестная x 2 .

. x 2 J

x

■ i

= b

12  0.4

_ |A j _ 21 3 _ 36 - 8.4

A 5  0.4

15 - 1.2

27.6

13.8

5  1.2

3  21

0.4

105 - 36 __69__₅ 15 - 1.2 = 13.8 =

Теорема Крамера. Если детерминант системы

единственное решение, которое находится по формулам

^Л ^ ⁰ , тогда система

^Л j

xj = —, J = 1, n Л

(1) имеет

^A j

X j = “T, J = 1, n

Формулы     д          называются формулами Крамера, а решение системы уравнений по этим формулам называется методом Крамера или детерминантов.

3 X j + 2 x ₂ + x₃ = 5

< 2 x j - x ₂ + x₃ = 6

x ^ + 5 x ₂ + 2 x₃ — —1.

Пример. Решите систему уравнений методом Крамера

Решение.

Л= 2   - 1  1

- 16

. Так как основной детерминант ∆ = -16 ≠ 0, система

имеет единственное решение и его найдем по формулам Крамера

Л 1

- 1  1

- 32

^Л 2 =

= 16

Л 3 =

- 1

,

—

- 1

,

6 =- 16

- 1         x 1 = 2 x ₂ = - 1 x ₃ = 1

Решение системы линейных уравнений методом Гаусса. Приведенные выше способы можно применять только при равенстве числа уравнений числу переменных. Метод, применяемый в общем случае, – метод Гаусса. Метод Гаусса еще называется методом последовательного исключения неизвестных. Элементарными преобразованиями над системой линейных уравнений называются следующие: умножение какого-либо уравнения системы на отличное от нуля число, перемена мест уравнений, умножение какого-либо уравнения на число и складывание с другим уравнением.

Образованная в результате этих преобразований система эквивалентна начальной, т.е. множество решений для обеих систем одинаково.

' an xi + ai2 x2 +••• + aijXj +••• + ainxn = b a21 x + a22x +••• + a2j xi +••• + a2„x„ = b —    —      —       —     —— ai1 xi + ai2 x 2 +••• + aijxj +••• + ainxn = b —      —       —       ——

• a. x,   a- x, +-----+ a. x. +-----+ ax„ = b,

m 1 1     m 2   2           mj i           mn nm образуем расширенную матрицу при помощи матрицы системы и столбца свободных членов

	x 1	x 2	x 3	x n
	Л a 11	a 12	a 13	a 1 n	| b 1
A —	a 21	a 22	a 23	a 2 n ■                                       |	| b 2
	a < ml	а э m 2	а . • m 3	a mn	| b m

Теорема Кронекера-Капелли. Если ранг матрицы системы равен рангу расширенной матрицы, т.е. если r ( A) = r ( A ) ,тогда система совместна, т.е. имеет решение.

Значит, можно сделать следующие выводы.

• 1.    Если r ( A) = ^r ( A ), система совместна.

• 2.    Если ^r ( A) * ^r ( A ), система несовместна.

• 3.    Если ^r ( A) = ^r ( A ) = ⁿ , система имеет единственное решение.

• 4.    Если ^r ( A) = ^r ( A ) <  ⁿ , система имеет бесконечное множество решений.

Пример. Решите систему методом Гаусса.

2 xj + x2 — x3 + 3 x4

<

5 x

— 3 x j

— x^ + 2 x3 — x4

+ 2 x2 — x ₃ + 2 x ₄ — 1

xj — x2 + 4 x3 — 2 x4

Решение. Решим систему методом Гаусса. В расширенной матрице системы удобно для вычислений: a ¹¹ = ¹ . Поэтому поменяем местами первую и четвертую строки

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №5 2025

4	_ 2	- 4 "		■ 1	-1	4	— 2	-4^
11	-4	-11	<->	0	-1	11	-4	-11
26	-7	-7		0	0	26	-7 19	-7 19
24	- 5	“5>		0 1	0	0	13	13 у

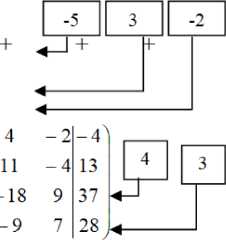
Расширенная матрица приведена к ступенчатому виду. Соответствующая ей система имеет следующий вид:

X - x ₂ + 4 x ₃ - 2 x ₄ = - 4 ^- x ₂ ^- 11 ^x ₃ ^- 4 x 4 = - 11 ’         26 x 3 ^- 7 x 4 = - 7

x# = L               13  4

- 7 + 7 X x =

Получим решения из последнего уравнения x4 = , из третьего        26, из х? = 11 +11X, - 4 X. = 7               X, = -4 + х, - 4 X, + 2 X, = 5

второго 2          3     4     и из первого 1         2     3     4.

Система однородных линейных уравнений. Если в системе линейных уравнений свободные члены равны нулю, т.е. если b1 = b2 =  = bm = 0, полученная система уравнений называется системой однородных уравнений, т.е.

a_n x₁ + a₁₂ x₂ +-----+ a_in X_n = 0

a₂₁ X j + a₂₂ x₂ +-----+ a_2n X_n = 0

a . X + a_mi Xi +-----+ a_m„ x„ = 0

m 1 1      m 2 2            mn n

Поскольку последний столбец расширенной матрицы этой системы равен нулю, ранги матрицы системы и расширенной матрицы будут равны, т.е. r ( A) = ^r ( A ) . Поэтому, согласно теореме Кронекера-Капелли, система однородных уравнений всегда совместна. Например, тривиальное решение (нулевое решение) системы будет (0,0,..., 0)=0.

Матричный вид системы уравнений следующий: AX = 0.

Согласно приведенным выше выводам 1-4, если r(A) = n система имеет единственное нулевое решение, если r(A) < n , имеет бесконечное множество решений. Значит, для того, чтобы система при m = n имела отличное от нуля решение необходимо и достаточно, чтобы ее детерминант был равен нулю.

Определение. Если задана система линейно независимых решений системы X,. X,X,.                                   „            „                    „   „      „

1,   2 ,  , k , произвольное решение этой системы X состоит из линейной комбинации л, л,•,л этих решений, т.е.     существуют такие числа      1,  2 ,  , k , что х — л х + лх2 + • + лх

1  1   2 2       k k тогда эта система называется системой фундаментальных решений.

Теорема. Если для системы r(A) < n , тогда произвольная система фундаментальных решений состоит из k = n- r(A) решений.

Например. Найдем систему фундаментальных решений системы однородных уравнений

<

3 X j + x₂

2 x

—

2 x

X j +11 x₂

I x i

—

—

—

—

8 x ₃ + 2 x ₄ + x ₅ — 0

3 x

—

7 x ₄ + 2 x₅

12 x ₃ + 34 x₄

5 x ₂ + 2 x₃

—

Последнее уравнение системы запишем

— 0

—

5 x

— 0

16 x ₄ + 3 x₅

— 0

первым, затем

приведем ее

к ступенчатому

виду:

—

—

л

—

—

3 7

—

—

3 7

—

—

—

—

—

—

—

—

—

—

—

⁵ 7

—

—

—

⁸ 7

■—

— 5

Ранг матрицы r(A) =2 . Базисный

минор переменных

x 1

и x 2

* 0,

выберем

переменные x 1 и x 2 как главные и выразим их через неглавные неизвестные x 3, x 4, x 5.

X j — 5 х ₂ + 2 х ₃ — 16 х ₄ + 3 х₅ — 0

8 х ₂ — 7 х ₃ + 25 х ₄ — 4 х₅ — 0

Заменим неглавные переменные x3, x4, x5 строками единичной матрицы E , чтобы найти систему общих решений. Если взять x3 = 1, x4 = 0, x5 = 0, система примет x1

—

следующий вид ¹

X 1 —(?;

решение:      7 ⁸

5 х ₂ + 2 — 0

8 х, — 7 — 0           ^X 1

2       отсюда

19       7

• — —, х ₂ — -

• 8     28

,

т.е. получим первое базисное

x ₃ — 0, x ₄ — 1, x₅ — 0

8;

1,0, 0 I

⁷ точно также

найдем еще

два базисных решения при

• X- — | ³

2    1 8

25        3

• -Т-; 0,1,0 1;

^{8         7} при Х 3 = 0, Х 4 = 0, Х 5 = 1

X — ⁽— 1;¹; 0, 0, 1 1 .

• ³ I 2  2           7

Найденные решения

1   2    3 образуют

заданной системы. Для соответственно на числа 8,

удобства перемножив

• 8,    2, образуем систему

фундаментальную систему решений X , X , X компоненты решений ^{1  2   3}

фундаментальных решений с целыми

X 1 — ( 19;7;8;0;0 )   X 2 — ( 3; - 25; 0; 8; 0 ) X — ( - 1; 1; 0; 0; 2 ) .

компонентами:                   ,                      ,  3

.

вычеркиванием первого, второго и т.д. столбцов матрицы системы уравнений. Если эти миноры отличны от нуля, тогда все решения этой системы линейных уравнений кратны этим числам. Например, найдем все решения системы линейных однородных уравнений x1 + 2 x 2 - x 3 = 0

< x 1 ^- x 2 + 3 x з = 0

2 x _x + x ₂ + 2 x₃ = 0

Сначала вычислим ранг соответствующей системе матрицы.

( 1	2	- 1 1		( 1	2	- 1 1		( 1	2	- 1 1
1	- 1	3		0	- 3	4		0	- 3	4
2 г	1	2 J	~	. 0	- 3	4 >	~	1 0	0	0 у

Значит, ранг матрицы системы уравнений равен r(A) = 2 и он на единицу меньше числа неизвестных. Поэтому число фундаментальных решений системы уравнений равно k =3-2=1. Возьмем произвольные два уравнения системы, например, первое и второе

Xj + 2x2 - x3 = 0

x — x2 + 3 x3 = 0

Вычислим знакочередующиеся миноры, полученные вычеркиванием первого, второго x1

и третьего столбцов соответствующей системе уравнений матрицы

- 1

- 1

• k = 5 k ,

x ₂

-

- 1

• k = - 4 k x₃

- 1

• k = -3 k

, здесь k произвольное число.

Значит, общее решение системы { 5 ^k ; ^{4 k} ; ^{3 k} } , здесь к произвольное число.