Нелинейная электрофизическая задача для сильноточных катодных узлов генераторов низкотемпературной плазмы

В физике и технике сильноточных плазменных систем (СПС) актуальной задачей является проблема повышения работоспособности и ресурса катодных узлов, функционирующих в экстремальных условиях по уровням тепловых потоков и плотностей тока [1; 2]. Решение ее требует многопараметрической оптимизации токовой нагрузки, радиационного и теплового потоков из плазмы разряда, электро - и теплофизических свойств материалов, геометрических размеров и характеристик теплообмена в конструкциях катодного узла. В настоящее время в СПС наиболее работоспособными показали себя электродные структуры, состоящие из стержневого электрода (вставки) из тугоплавкого металла, запрессованного в интенсивно охлаждаемый корпус катододержателя (обоймы) [3; 4]. В мощных плазменных установках, например, в плавильных плазмотронах до 15 кА [5–8] токовая нагрузка внутри катодного узла становится решающим фактором функционирования и ресурса работы конструкции. Экспериментальная оптимизация катодных узлов по токовому режиму является трудоемким и дорогостоящим процессом и не обладает обобщенностью полученных результатов.

Теоретический подход к данной проблеме состоит в решении краевой электрофизической задачи, установлении закономерностей и вклада джоулевой диссипации в энергообмене катодного узла. В работах [9–13] краевая задача решается в различных постановках для катода- вставки и не рассматривается прохождение тока в объеме массивного катододержателя – обоймы.

В данной работе впервые краевая электрофизическая задача решается в строгой постановке для катодного узла, т.е. для системы «вставка – обойма» в целом.

Постановка задачи

На рис. 1 показана полуплоскость осевого сечения расчетной модели катодного узла СПС, составленного из двух соосно сопряженных элементов цилиндрической симметрии. На торец стержневого катода I в пределах контакта с плазмой разряда размером r 0 поступает электрический ток с плотностью: j 0 = F ( r ), где F ( r ) – в общем случае известная функция, r и z – цилиндрические координаты.

Теоретическое исследование стационарного распределения потенциала электрического поля в катодном узле состоит в решении уравнения неразрывности тока:

divj c - 0                                               (1)

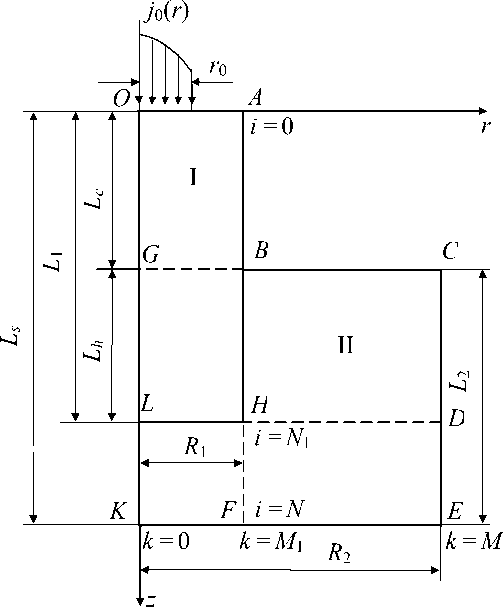
Рис. 1. Расчетная модель катодного узла

I – катод (вставка), II – катододержатель (обойма)

Для рассматриваемой осесимметричной модели уравнение (1) в двумерном приближении примет вид:

где

jc -\ Jr + jz

Jr --

1 ⁹ r d U r d r p ( T ) d r

1 d U

p dr

и Jz --

d 1 d U

d z p ( T ) d z

1 dU p dz

= 0,

Граничные условия к уравнению (2) следующие:

1) на горячем торце катода (линия OA )

1    д и ( r ,0 )

Pi (T)   az

-Ц, 0 <  r <  r o ^{n r} 0

[ 0, r o <  r <  A i

• 2)    на горячем торце катододержателя ( BC )

d U ( r , Lc ) д z

= 0, R 1 <  r <  R 2

• 3)    на холодном торце катододержателя ( KE )

U ( r , Ls ) = 0, 0 <  r <  R 2

• 4)    на оси катодного узла ( OK )

» UM = 0, 0 <  z <  Ls

• 5)    на цилиндрической поверхности катода ( AB )

^{5 U}^z) = 0, 0 < z < Lc

• 6)    на цилиндрической поверхности катододержателя ( CE )

U ( R 2 , z ) = 0, L _c <  z <  Ls

В выражениях (2) – (8) приняты следующие обозначения:

P i,2 ( T) — удельное электросопротивление материалов катодного узла соответственно катода и обоймы; U – потенциал электрического поля; I – разрядный ток; j 1 , j 2 – плотность тока в катоде и обойме соответственно.

На контакте двух металлов поставлены граничные условия 4-го рода:

U 1 = U 2 ,

a U,

^ 1 = ^

¹ d n ²

a u 2 d n

где n – нормаль к внутренней границе, направленная вдоль z на поверхности LH или вдоль r на ВН (см. рис. 1).

Метод решения

Электрофизическая задача в рассмотренной выше постановке аналитически не решается. Поэтому используем метод конечных разностей[14]. Для получения стационарного распределения электрического потенциала внутри катодной структуры вместо уравнения (2)

решаем нестационарное уравнение неразрывности тока методом установления в следующем виде:

д и 1,2 =      а² и 1,2 + 1 д( _r ⁵ и 1,2

дт ^1,2 д z ²     r д r ( д r

Для придания алгоритму решения универсальности следует перейти к безразмерным переменным. После обезразмеривания уравнение (10) запишется как

дТ = дт "д^У.) <дz 2 J + " 1 ду д2 у 2 ^ r^ д r д r^2 v дx " д2 x ^ " 1 дx д2 x ) --= + + дт 1дz 2; ^ 1- дr1 д 1-2 J соответственно для элементов I и II электродной структуры.

Область интегрирования I - II, занимаемую катодным узлом, разбиваем пространственной сеткой

^ h ₂ = ® h ^x ® h ₂

zi = th,, h > 0, i = 0,1,2,...N; Nh1 = Ls rk = kh2, h2 > 0, k = 0,1,2,..M; Mh2 = R2

с шагами h ₁ по координате z и h ₂ по r . По временной координате введем равномерную сетку ®_т = { tj = j T ₀, т ₀ >  0, j = 0,1,2,... } с шагом т ₀.

Значение сеточной функции у (или x ) в некотором узле сетки ( z, r _k , tj ) обозначим y j_k .

Соответственно у ⁽ z, ± 1 , ^rk ± 1 , tj ) = yj , к ) _{± 1}, у ⁽ z , ^rk , tj _{+ 1}) = у^ .

На 4-х точечном шаблоне расчетной пространственно-временной сетки дифференциальное уравнение (10) аппроксимируется разностным уравнением:

vj+1 - jA+1 - 7 vj+1 + +1 IT 12 + ( +1 - vj+1 1                 + y i, k y i, k = ( y i-1 2 y i + y i+1 ) /( h1 ' Ls ) +( yk+1 yk-1 ) /2 k (h 2/ R 2) +

+ ( y £* - 2 yj ^{+ 1} + 2 yk + 1 ) /( h / R 2 )²,                                                      ⁽¹³⁾

где o (yj) - удельная проводимость на j -том временном слое. Погрешность аппроксимации имеет порядок 0( h ²+ т ). Применяя локально-одномерную схему прогонки метода дробных шагов, уравнение (13) разбиваем на два одномерных:

У i ^{+ 1} - У i = 2 ( у    - 2 yj ^{+ 1} + y /₊ 1 ) /( h_x / Ls )²

yk ^{+ 1} - yk = 2 ( ( yk + 1 - y ^¹ ) /2 k ( h 2 / R 2 )² + ( yk + 1 - 2 у + 2 yk + 1 ) /( h 2 / R > )              (15)

соответственно по координатам z и r . При прогонке разностные уравнения (14) и (15) приводятся к алгебраической системе уравнений типа:

4-Ум- c-у-+ Biyi+1 = - Fi с условиями Ai, Bi > 0, Ci > Ai + Bi, обеспечивающими разрешимость системы методом прогонки. Решение задачи ищем в виде:

y_t= «i + 1 y_{l +} 1 + Д₊ 1 , i = 0,1,2,... N - 1,                                      (17)

где коэффициенты а1+1 и р1+1 вычисляются по рекуррентным соотношениям а+1 = B / (C - Аа), в+1 = (F - A А-) / (C - 4а-)                      п

Значения начальных прогоночных коэффициентов « 1 и p i определяются при помощи одного из граничных условий области интегрирования. Затем из второго граничного условия находим значения сеточной функции y _N и по формуле (17) вычисляем все остальные значения у _i вплоть до у ₀. При этом переход от временного слоя j на слой ( /' +1) осуществляется последовательным решением однородных уравнений (14) и (15) по соответствующим координатам.

Так как катодный узел состоит из сопряженных элементов разной геометрии, необходимо разбить его на несколько простых областей и для каждой решать свой прогоночный цикл, «сшивая» соседние области удовлетворением единым граничным условиям. Для прогонки по координате z выделяются области OAFK и BCEF, а по координате r области OABG, GCDL и LDEK. Следует отметить особенность прогонки по областям OAFK и GCDL. Здесь используется метод встречных прогонок: из граничных условий вычисляются начальные коэффициенты α1I и β1I для первого элемента, α1II и β1II для второго элемента, а искомая функция на их границе определяется из условий сопряжения.

Составленный алгоритм позволяет рассчитать стационарное распределение электрического потенциала в составном катодном узле.