Нелинейная математическая модель функционирования педагогической системы

Актуальность. Математическое моделирование поведения социальных, в частности педагогических систем (ПС), в период кризиса – актуальная задача сегодняшнего дня. Математические модели функционирования социально-педагогических систем рассматриваются в работах В. П., Милованова, В. И. Жегалова, С. Н. Киясова и др. [Милованов 2001; Жегалов, Киясов 2007], в которых синергетическое моделирование ведется на языке нелинейных дифференциальных уравнений. Кризис в таких моделях представлен как точка бифуркации, после которой система выбирает одну из возможных траекторий развития. Происходящее в точке бифуркации скрыто от внешнего наблюдателя. Вызывает интерес описание процессов внутри этого «черного ящика» с точки зрения внутреннего наблюдателя.

На основании наблюдений и экспериментов было установлено, что система информационных потоков в период кризиса имеет четкую структурную организацию, общую для социально-педагогических систем различной природы [Сибирев, Сибирева 2016: 236]. Эмпирически наблюдаемые свойства системы в кризис перекликаются со свойствами странного аттрактора Лоренца, состоящего из множества многократно проходимых петель, обладающего «масштабной инвариантностью» (т.е. «в мелком масштабе он выглядит примерно так же, как и в крупном») [Малинецкий 2007:101]. Это определило выбор математического аппарата данной статьи.

Кризис – период становления новой программы стабильного функционирования (гомеостаза) ПС. Среди происходящих в период кризиса процессов (подробнее см. [Сибирев, Сибирева 2016:236]) определяющими являются: z(t) -деятельность по построению новых целей, y(t) - деятельность по созданию организационной структуры новой программы гомеостаза, x(t) - деятельность по выбору фактического содержания новой программы. Поведение педагогической системы в период кризиса можно описать системой дифференциальных уравнений:

f dx

— = -kx-av. dr

— = bx+bv-cx~ d- ,

; — = -d2 + тху

Система (1) связывает величины x, y, z с помощью положительных параметров k, a, b, c, d, m, которые характеризуют влияние внешних и внутренних сред на систему. Так как они изменяются медленнее, чем создается новая целевая программа функционирования, считаем их постоянными. Коэффициенты при х и у во втором уравнении, вообще говоря, различны, но наблюдения показывают, что процессы по выбору фактического содержания новой программы и построения ее организационной структуры происходят синхронно, поэтому можно брать равные коэффициенты при линейных слагаемых во втором уравнении.

Модель, описываемая системой нелинейных дифференциальных уравнений, аналогичная (1), исследовалась в [Коноплева, Сибирева 2018: 105–107] методами, указанными в [Гурина, Дорофеев 2010: 65–66], а именно: преобразованиями и исключением переменных система (1) приводилась к виду, в котором гомоклинической петле соответствует гетероклиническая траектория, с последующей проверкой стыковки частей этой траектории, что доказывает существование хаотического аттрактора Лоренца.

Характеристическое уравнение, соответствующее линеаризованной системе, при любых значениях параметров имеет два отрицательных и один положительный корень. Следовательно, система (1) имеет 3 особые точки:

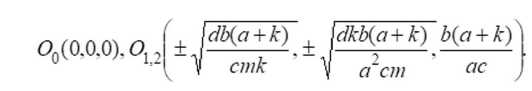
точка О 0 (0,0,0) - седло-узел с двумерным устойчивым и одномерным неустойчивым инвариантными многообразиями (всюду далее используется терминология [Шильников, Шильников 2004]).

Используя топологические методы нелинейной динамики, в том числе метод характеристических показателей Ляпунова [Никитина 2014: 69–71], определим гомо клинические траектории седло-узла Оо(0,0,0), разрушение которых при изменении значений управляющих параметров приводит к бифуркации гомоклинического каскада (хаотического аттрактора).

Введем малые отклонения 8x, 8y, 8z в системе (1) от частных решений x, y, z и составим уравнения в вариациях

. (3)

• 8—    = -Абх + (78г. б— = Q) - cz)8r + 68т - cx6z. 6— at               at                           at

Характеристическое уравнение системы (3) имеет вид

• >? + Л² (d + к - b) + /4d(k -Ь)-Ь(к + о) + c(nix~ + az)) + d(-b(k + а) + acz) +

и определяет характеристические показатели любой особой точки в поле трехмерного пространства системы (1).

Проведем численное исследование системы (1) при следующих значениях управляющих параметров [Гурина, Дорофеев 2010: 67]:

( a , b , c , m , k ) = (1, 4, 8, 4,1)    d e (2,..., 2,3345)

При малых изменениях значений коэффициента d может существенно измениться динамика решений. Следовательно, параметр d, характеризующий способность системы к целеполаганию, является бифуркационным. Практическое подтверждение этого можно найти в работах по менеджменту, где указано, что целеполагание определяющим образом влияет на поведение системы.

Из уравнения (4) следует, что особая точка О ₀ системы (1) является седло-узлом для указанных значений параметров, и в О ₀ седловая величина о ₀ =Х 1 +Х ₂ + Х ₃ <0 для параметров (5).

Выделим в правых частях системы (3) слагаемые линеаризации (1). Остальные члены содержат частные решения x,y,z . Они могут влиять лишь на мнимую часть характеристических показателей. Тогда седловая величина для всех точек пространства, порожденных системой дифференциальных уравнений (1), будет одинаковой, и бифуркационный процесс описывает теорема Гробмана–Хартмана [Шильников, Шильников 2009: 79]: «Пусть точка О0 есть грубое состояние равновесия. Тогда существуют окрестности U1 и U2, в которых исходная и линеаризованная системы топологически эквивалентны». Т.е. окрестность, заполненная седлоузловыми точками, переходит седлофокусный континиум. Седлофокусная петля имеет отрицательную седловую величину о во всех точках траектории для рассматриваемых параметров (5). Численными методами определяется, что сумма показателей Ляпунова системы (1) для параметров (5) отрицательна, а это означает существование гомоклинической траектории седлофокусной петли.

-0,8    -0,4      0      0,4       *              -и -44     0      64 х

_                                             а                                        6

Рис. 1. Проекции решения системы (1) на плоскость О xy ( а – при d =2, б - при d =2,33)

На Рис. 1 приведены проекции численных решений системы (1) на плоскость О xy (рис. 1(а) при d= 2 , рис. 2 (б) при d= 2,3 ). При d= 2 нет четкого разделения на деятельность организационного и содержательного характера, это единый процесс. При небольшом увеличении параметра d= 2,3 точка O включена в петлю траектории (рис. 1 (б)). На Рис. 1(б) полужирной линией обозначены траектории, содержащие седлофокусные точки, тонкой линией - седлоузловые. Система начинает разделять организационную деятельность и деятельность по созданию фактического содержания программы, осуществляя произвольный выход то на одну, то на другую петлю.

Возрастание коэффициента d приводит образованию траектории относительно особых точек Ο₁ и Ο₂ . Физическая интерпретация этого факта: увеличение диссипации вызывает увеличение притяжения, увеличение отрицательной седловой величины σ во всех точках траектории приводит к разделению предельного цикла на два.

Для педагогических и иных систем это означает, что жизнь организационных структур протекает независимо от содержания, для реализации которого они создаются.

На рис. 2, а, б, в представлены проекции на координатные плоскости при d= 2,4

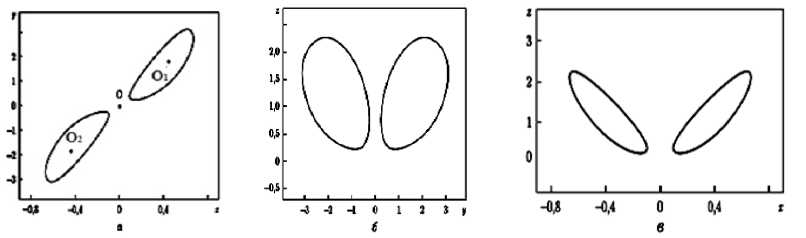
Рис. 2. Проекции решения системы (1) на координатные плоскости, d= 2,4

Структура типа странного аттрактора рождается за пределами значения параметра d , рассматриваемого в (5). Области существования замкнутой траектории относительно особых точек 0 1 и 0 2 не пересекаются. Порождается орбитальная неустойчивость, которая сопровождается перескоком изображающей точки с одной орбиты на другую. Т.е. увеличение параметра d усиливает хаотизацию процесса.

Рассмотрены также средневыборочные значения управляющих параметров - коэффициентов системы (1)

a=18,2; b=18,8; c=9,75; d=32,7; m=8,4; k=8,4 (6)

полученные экспериментально [Сибирева, Гумирова 2018: 88-95] в соответствии с методикой «оценки самоорганизации деятельности» [Мандрикова 2010: 59], предлагающей тест для оценки в баллах величин, сопоставимых по смыслу с коэффициентами системы (1). Для этих значений коэффициентов седлофокусная петля имеет положительную седловую величину σ во всех точках траектории. Сумма показателей Ляпунова в этом случае положительна, что свидетельствует о хаотическом поведении системы: с увеличением скорости целеполагания происходит отдаление организационных структур (и их действий) от процесса смыслового наполнения новой программы гомеостаза, что ведет к негативному сценарию протекания кризиса.

Вывод. Каждая наука в своем развитии проходит различные этапы: от эмпирических наблюдений – к сбору и классификации фактов, далее к их математическому описанию и анализу. В последнее время такой переход наблюдается в социальных науках. Междисциплинарной методологией при этом выступает синергетика, описывающая поведение сложных открытых систем в терминах нелинейных дифференциальных уравнений. При этом математическое описание поведения систем согласуется с эмпирическими наблюдениями и с результатами экспериментов (в том числе и педагогических).

Математические модели, описывающие поведение ПС в кризис, углубляют наши знания о характере его протекания, позволяют прогнозировать некоторые возможные сценарии развития. Проведение численных расчетов с адекватной моделью позволяет избежать экспериментов с созданием кризисных ситуаций, нежелательных в реальной жизни или недоступных исследователю. Дальнейшие исследования в данном направлении позволят проводить диагностику динамики кризиса, выработать соответствующие методики и рекомендации по кризисному сопровождению и управлению педагогических и социальных систем.