Нелинейная отражательная эллипсометрия для анизотропного одноосного кристалла в случае, когда оптическая ось лежит в плоскости падения

В настоящее время актуальным предметом исследования являются оптически изотропные и анизотропные среды (одноосные кристаллы), тонкие пленки на их поверхности, оптически активные среды [1; 2].

Возможности получения сильных нелинейных эффектов в кристаллах в значительной мере связаны с большой концентрацией частиц и наличием широкого класса оптических материалов без центра инверсии, допускающих существование нелинейных эффектов, квадратичных по полю.

На сегодняшний день линейная эллипсометрия является признанным методом диагностики материалов, поскольку использует векторный характер светового поля [2]. Однако для более детального анализа свойств вещества широко применяют нелинейно-оптические методы или нелинейную оптическую спектроскопию [3], которая во многих областях также хорошо себя зарекомендовала. Тем не менее остается неразработанным метод нелинейной эллипсометрии.

В этой связи целью данной работы является проведение эллипсометрических исследований анизотропных кристаллов новым методом – нелинейной эллипсометрией отраженной второй гармоники.

Расчет отраженной второй гармоники для в случае, когда на границу раздела падает р-поляризованная электромагнитная волна

Займемся выводом основных соотношений для расчета энергетического коэффициента отражения одноосного кристалла с различной ориентацией оптической оси в случае генерации второй гармоники.

Пусть на границу раздела двух сред воздух – нелинейный одноосный кристалл – плоскость z = 0 распространяется р-поляризованная волна. Нас интересует распространение волн в крис- талле.

Нелинейное волновое уравнение, которое описывает распространение световой волны в среде (1), имеет следующий вид:

rotrotE +

1 д ² D L "7 I t ²"

4 п д ² P NL c ² д t ²

Вектор нелинейной индукции D дается выражением [4]:

D = D L + 4п P NL .

Для анизотропной среды каждая компонента вектора D связана линейно с компонентами поля E j через тензор диэлектрической проницаемости [5].

При учете нелинейности в среде возникает взаимодействие волн. Простейший случай взаи- модействия световых волн реализуется при нелинейно-оптических эффектах второго порядка [6].

В случае когда оптическая ось лежит в плоскости падения, тензор диэлектрической прони-

цаемости для одноосного кристалла имеет вид ^Б хх о   Б XZ Б= о   Буу   о .                             (3) ч Б XZ    о Б ZZ > Компоненты тензора диэлектрической прони- цаемости в выражении (3) имеют вид [7]

бхх = бo cos2 а + бe sin2а, б xz = (б e-б o )sin а cos а,

• •     _                                                   (4)

^б уу = ^{б e} ,

• • 2„ ,            2„

б _zz = б _o sin а + б _e cos а.

Тогда в соответствии с (3) соотношение для вектора D запишется в виде

D ^L =^б xx ^E x ^+б xz ^E z ,

D =б yy E y ,                           (5)

_ D z = ^Б XZ ^E X ^{+ Б} ZZ ^E Z .

Подставим первое уравнение системы (5) в волновое уравнение (1), предварительно спроецировав его на оси главной системы координат, в результате получим для проекции на ось х :

=. б   д ² E     б_ д ² E,

(rotrotE) х + х^--х + ^z—X = c2 д t2     c2 д t

₌ 4п д ² P ^

2 Л+2 .

c    д t

Вид нелинейной поляризации с учетом падающей плоской волны

P ^NL «X ⁽²⁾ : E ² e ^{2 к} I ^х . e ^{2 к}" e - i ^{2 ш} t .               (7)

Пусть напряженность электрического поля E в дифференциальном уравнении (6) представле- на в виде плоской волны:

E = E ( z ) e - i ^{2 ш} t e i ^{2 к 1 х}

С учетом дифференциального оператора Лапласа А в декартовой системе координат и с учетом вида волнового вектора, согласно рис. 1, оператор rotrotE примет следующий вид:

, -    д2E д2E rotrotE =--- +--— .                           (9)

д х ² д Z ²

Подставив (8) и (9) в уравнение (6), выполнив необходимые преобразования, приведя подобные и учтя к о = to/ c , получим:

^-^ + 4(^Б хх - к ,2 ) E x ( Z ) + 4 к 2 Б xz E z ( Z ) = д z

= -16 л k 0 P ^Le^{1 2 k}® ^Z .

Аналогично получаются выражения для у- и Z -компонент. Таким образом получаем систему уравнений:

д ² E „. ( z )

• -   + 4^{( к} о ^Б хх ^{- к} || ) ^E x ^{( Z} ) ^{+ 4 k} 0 ^Б xz ^E z ^{( Z} ) =

д Z ²                    "

2 NL i 2 к <^ц z

= -16пкоРх e Z , д2 Ey(z )       2        2

-------- + 4(к0 Буу - к" )Ey (Z) = д z 2

= -16п к2 P^e12 к™Z, д2 E, ( z )

-----— + 4коБXZEX(Z) + 4(к0БZZ - к|| )Ez(Z) = д Z 2                                    "

= -16п к2 P^e^{1 2 kZ1) Z} .

В случае р-поляризации система уравнений (11) перепишется в следующем виде:

^- ^ х М + 4( к о² Б хх - к 2 ) E x ( Z ) + 4 к 2 Б xz E z ( Z ) = д Z ²

= -16п к 2 P N^L e i ^{2 k Z1) Z} ,

• ₂ ^{о х} ,                                 (12)

z^ + 4к2БXZEX(Z) + 4(к2БZZ - к2)EZ(Z) = д Z

= -16п к 2 P _Z ^NL e i ^{2 kZ1) Z} .

Общее решение системы (12) имеет вид (13)

E_x ( z ) = E_xe ^- i ^{X 1 Z} + E_xe ^{i X 1 Z} +

4п к о² ( nP z^NL - mP x^NL ) i 2 к z

+----------------5--------e Z ml - n2

E_z ( z ) = E,e ^- i ^X 2 ^Z + E_ze i ^X 2 ^Z + ZZ   Z

4П к о² ( nP N^L - lP N ) i 2 kZ^)Z

_         ml - n ²               ,

где

X 1 =± i {[ к о2 (Б хх +Б zz ) - 2 к |2 -

^{(( к} о ^{( б} хх ^+Б zz )   ^{2 к} " )    ^{4( к} о ^{( б} хх ^Б zz   ^Б xz )

^{- к} о к ^{2 ( б} хх ^{+ Б} zz ) ^{+ к} |4 ^{)) 1/2 ]} / ^{2} 1/2} , 1 2 =± i {[ к о² (Б хх +Б zz ) - 2 к |2 +

^{+ (( к} о ^{( б} хх ^+Б zz ) ^{2 к} " ) ^{4( к} о ^{( б} хх ^Б zz ^Б xz )

- к о² к ,2 (Б хх +Б zz ) + к |4 )) ^1/2 ]/2} ^1/2 .

Запишем граничные условия для полей Ё и ЕЕ. Тангенсальные компоненты E и ЕЁ непрерывны на границе раздела:

' E . (М z = 0 - = E . (M z = 0 + - \ Hy И z = 0 - = Hy (2“)| z = 0 + .

Для известной напряженности электрического поля E из уравнений Максвелла легко можно найти выражение для напряженности магнитного поля H

H = —г I Xi E_xe i ^{-X 1} z ^y    2% I 1 .

+

8n k g² k zH nP z^NL - mP NL ) i 2 kz»z

+                2          e ml - n

Далее, подставив (13) и (16) в граничные условия (15), соответственно получим систему урав-

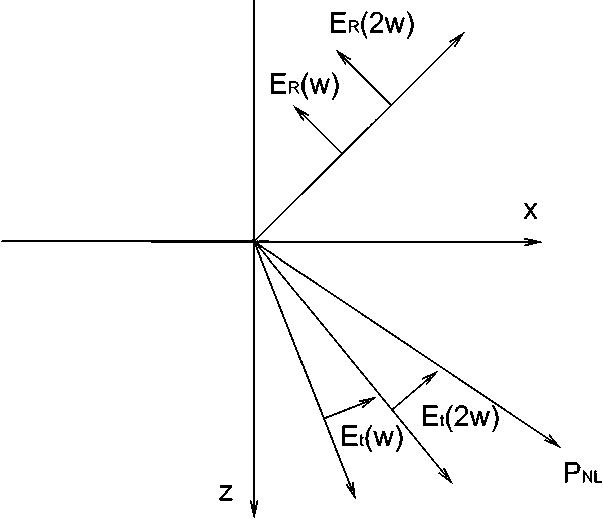
Рис. 1. Волны на границе среды, поляризованные в плоскости отражения

нений и, разрешив ее относительно амплитуд E_R ^p и E_t ^p , приведем ее к следующему виду:

E p =

R

E p =

P 2 (2 k z ⁱ⁾ -% ! )

ⁿ 1 ^-X 1

в д (2 к Х -П 1 )

П 1 ^-X 1

Для дальнейшего расчета необходимо ввести зависимость как выглядит вектор нелинейной

поляризации.

Когда падают две волны одинаковой частоты, для случая генерации второй гармоники нелинейная поляризация имеет вид [4]

где введены следующие обозначения:

'    4n k 2 ( nP NL - mP NL )

. ^{₽ 2} = —m . —,          (18)

,4 1 = V ^k 2 ^- k ² .

В случае s-поляр и зации в систе м е ( 1 1) о стается только второе уравнение.

Общее решение данного волнового уравнения имеет вид

E _y ( z ) = E y e i 2^⁽ k 2 ^{s yy k 2)} z + E y e i^k^{0 8 yy k} 2 ) ^z -

4n ^k 2 P NL    „ 2 2 k «> z

z

_{2           2      2} e .

k08yy - k|| - kz

С учетом граничных условий аналогично слу- чаю p-поляризации получим амплитуды волн отраженной и прошедшей компонент:

„ 5    Р 1 (П 2 E R =	- 2 k z i)) ,
<             П 1	-п 2	(20)
E 5 = в 1 (П 1	- 2 k z 1)) .
[ t        П 1	-п 2

В системе (20) введены обозначения:

2 NL

₌    ^{4n k} 0 ^P y

^{P 1}        2„        7.2    7.2 ,

k08yy - k|| - kz

• ⁿ 1 =V ^k 2 ^- k ² ,

• ⁿ 2 = ^( k ^{2 8} yy ^- k ² ) *

  
  

  Гр л P . P y P		=
  	z
  	I d	11	d 12	d 13	d 14
  =	d	21	d 22	d 23	d 24
  	I d	31	d 32	d 33	d 34

  
  

  	I f2 1 E . E 2	(22)
  d 15 d 16 )	y
  d 25 d 26	E z	*
  d 35 d 36 J	2E z E y
  	2 E z E .
  	[2E . E y J

  
  

Для дальнейшего расчета необходимо учесть ориентацию оси кристалла, поэтому необходи- мо повернуть оптическую ось относительно оси z главной системы координат с использованием матрицы поворота, приведенной в книге [8]:

IP NL 1 P .	|cos a		0	- sin a?	IP NL 1 P .
P NL	=	0	1	0	Py NL	.              (23)
P NL, I z J		v sin a	0	cos a v	P NL, I z J

Далее займемся расчетом эллипсометрических параметров отраженного света.

Пусть на полуограниченную среду падает поляризованная электромагнитная волна (рис. 1) с длиной волны 1.06 мкм, соо т ветс т венно, отраженная вторая гармоника имеет длину волны 0.53 мкм.

В случае нелинейной отражательной эллипсометрии с учетом (17) и (20) выражения для р, которое входит в состав основного уравнения эллипсометрии [9],

Р= R p/ R s ,

или часто бывает удобнее записывать р в виде

р = tg v е^{г А} ,

примет следующий вид:

Р=

3 o (^{2 k} Z ¹^ ^— ^ 1 ) K1 ^— ^ 1 Р 1 (Л о ^{— 0 k} Z ¹) ) H1 ^— П 0

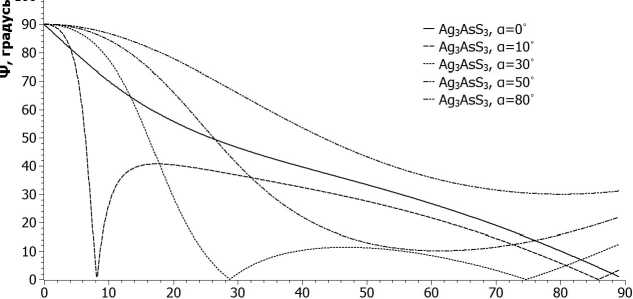
0, градусы

Рис. 2. Зависимость эллипсометрического угла v от угла падения 6 для кристалла прустит при ориентации оптической оси на угол а = 0 ° , 10 ° , 30 ° , 50 ° , 80 °

где

в 1

4 n k Py L

0 ° yy

—

^

—

2 , k_z

П 1

—

^k i0-

П 2

= 2#02 ^e УУ

—

k ° ).

в 2

= 4 n k 0 ( nP_z ^NL

—

mP_x^ ^NL )

ml — n ²

.

Соответственно, в (27)

введены следующие

обозначения: k ₀

–

NL P_z

. _nNL _nNL волновое число; P , P , x^y

– компоненты вектора нелинейной поляри-

зации; константы l , m , n определяются из выражения

L    0°xx m = k^ zz

—

к

—

n = k 2 £ _xz ;

—

k«

k || = к о n sin 6;

^k z = П 1 =

—

k z ² ,

—

k z ² ,

^k 2 .

Данные одноосные кристаллы (в-борат бария (BBO), ниобат лития, прустит) принадлежат к симметрии 3m [10]:

Известные компоненты тензора нелинейной восприимчивости для кристалла (в-борат бария (BBO):

d00(1.06 мкм) = 5.5 • 10—9 ед. СГС, d31(1.06 мкм) = 0.4 • 10—9 ед. СГС;

для ниобата лития – d00(1.06 мкм) = (5.0 ± 0.50) • 10—9 ед. СГС, d31(1.06 мкм) = (—10.39 ± 1.05) • 10—9 ед. СГС, d33(1.06 мкм) = (—65 ± 6.4) • 10—9 ед. СГС;

для прустита – d22(10.6 мкм) = (39.6 ± 6) • 10—9 ед. СГС, d31(10.6 мкм) = (04.8 ± 5.3) • 10—9 ед. СГС [10].

Тензор диэлектрической проницаемости для одноосного кристалла имеет вид (3).

Численные значения показателей преломления обыкновенной и необыкновенной световых волн, для представленных одноосных кристаллов:

BBO – no(1,06 pm) = 1,65451, ne(1,06 pm) = 1,53919; ниобат лития – no(1,06 pm) = 0,03339, ne(1,06 pm) = 0,14386;

прустит – no(10,6 pm) = 0,6966, ne(10,6 pm) = 0,5033.

Рассчитаем для данных кристаллов эллипсометрические зависимости при различной ориентации оптической оси. При расчете воспользуемся формулами (04)-(05), где р находится из формулы (26). Ниже посторим зависимости для значений угла ориентации оптической оси а = 0°, 10°, 30°, 50°, 80° соответственно. Угол падения будем менять в пределах от 0 до 90°. Для эллипсометрического угла v данная зависимость от угла падения 6 представлена на рис. 0.

Зависимость, изображенная на рис. 2, носит затухающий характер с явно выделенными минимумами 6 = 8° и 86° для ориентации оси на угол а = 10°, 6 = 08,6° и 74,5 для ориентации оси на угол а = 30°. Для значения угла а = 80° зависимость эллипсометрического угла v убывает до 30° при 6 = 80° и, далее, возрастает до 31°; для значения угла а = 50° зависимость эллипсометрического угла v убывает до 10° при 9 = 57,5° и, далее, возрастает до 01°.

Необходимо отметить, что для некоторых значений ориентации оптической оси имеется по два псевдобрюстеровских угла, что отличает нелинейную эллипсометрию от линейной. По линейной эллипсометрии в настоящее время существует целый ряд публикаций – тезисов, статей, монографий [9].

Зависимость для эллипсометрического угла А не будем приводить, так как она является мало информативной. Отметим, лишь то, что вблизи

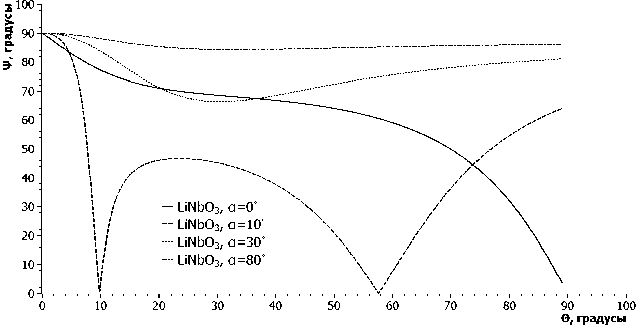
Рис. 3. Зависимость эллипсометрического угла у от угла падения 6 для кристалла ниобат лития при ориентации оптической оси на угол а = 0 ° , 10 ° , 30 ° , 80 °

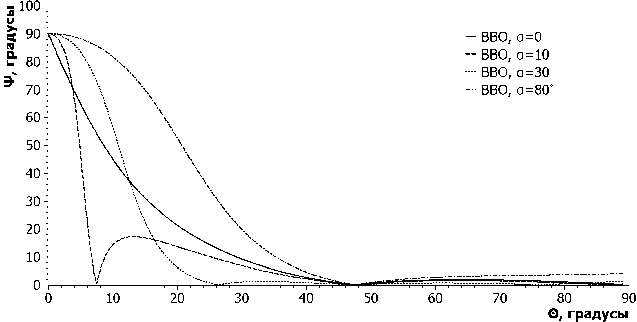
Рис. 4. Зависимость эллипсометрического угла у от угла падения 6 для кристалла в -борат бария при ориентации оптической оси на угол а = 0 ° , 10 ° , 30 ° , 80 °

псевдобрюстеровских углов значение эллипсометрического угла А меняется на п.

Там, где значение эллипсометрического угла А остается постоянным и равно нулю или 180 градусам, поляризация не меняется.

В общем случае падения эллиптически поляризованной волны в местах, где фаза меняется на п, отраженная вторая гармоника будет иметь линейную поляризацию.

Далее на рис. 3 представлена зависимость эллипсометрического угла у для кристалла нио-бат лития от угла падения.

Данная зависимость имеет схожий характер с зависимостью эллипсометрического угла у для кристалла прустит (см. рис. 2).

Приведенная зависимость имеет явно выделенные минимумы 6 = 10° и 57,5° для ориентации оси на угол а = 10°. Для значения угла а = 30° зависимость эллипсометрического угла у убывает до 66° при 6 = 30° и, далее, возрастает до 82°.

На рис. 4 представлены зависимости эллипсометрического угла у для кристалла в-борат бария.

Данные зависимости имеют схожий характер. Отличие состоит в том, что при любой рассмотренной ориентации оси у эллипсометрических зависимостей угла у от угла падения для данного кристалла (см. рис. 4) имеется псевдобрюс-теровский угол 6 = 47,5°. Соответственно, фаза вблизи этого значения скачком меняется на п.

Заключение

В данной работе проведены эллипсометрические исследования анизотропных кристаллов новым методом, нелинейной эллипсометрией отраженной второй гармоники. В рамках данного исследования получены соотношения отражательной нелинейной эллипсометрии в случае, когда оптическая ось лежит в плоскости падения.

Рассчитаны параметры и угловые спектры нелинейной отражательной эллипсометрии для одноосных кристаллов (в-борат бария, ниобат лития, прустит) с различной ориентацией оптической оси.

Для некоторых значений ориентации оптической оси имеется по два псевдобрюстеровских угла, что отличает нелинейную эллипсометрию от линейной.

У всех представленных зависимостей вблизи псевдобрюстеровских углов значение эллипсометрического угла А меняется на п. Там, где значение эллипсометрического угла А остается постоянным и равно нулю или 180 градусам, поляризация не меняется.

Для представленных кристаллов эллипсометрические зависимости имеют схожий характер. Это связано с характерным для них видом тензора нелинейной восприимчивости. Также можно видеть различия в методах линейной и нелинейной эллипсометрии, которые четко подчеркивают ориентацию оптической оси. В линейном случае данный эффект проявляется слабо и зависит только от ориентации оптической оси. В случае нелинейной эллипсометрии данный эффект ярко выражен.

При угле падения 6 = 0° значение эллипсометрического угла у равно 90°. Это говорит о том, что поляризация отраженной волны меняет свой азимут на 90° (рис. 4) независимо от того, какую поляризацию имеет падающая волна.