Нелинейная сингулярно возмущенная задача Коши с внутренним слоем

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                        

Рассмотрим задачу Коши у' (t) = y(t)(1-y(t)),te(0, К)                               (1)

У(0) = В,                                                 (2)

где 0< ε — малый параметр [1–9].

Правую часть уравнения (1) обозначим через F ( y ), т. е. F ( y )= y (1- y ). Уравнение (1) имеет две точки равновесия (стационарные точки):

y (1- y )=0 ⇒ y 1 =0 или у 2 =1.

Определим тип этих точек равновесия:

F' ( y )=( y - y ²)'=1-2 y

F '( y 1 )=1-0=1>0; F '( y 2 )=1-2=-1<0.

Отсюда следует, что точка y 1 =0 – неустойчивое положение точки покоя, так как F '( y 1 ) >0; а точка y 2 =1 — устойчивое положение точки покоя, так как F '( y 2 )<0.

Построим график функций F ( y ). В двух точках покоя производная искомой функций равна нулю.

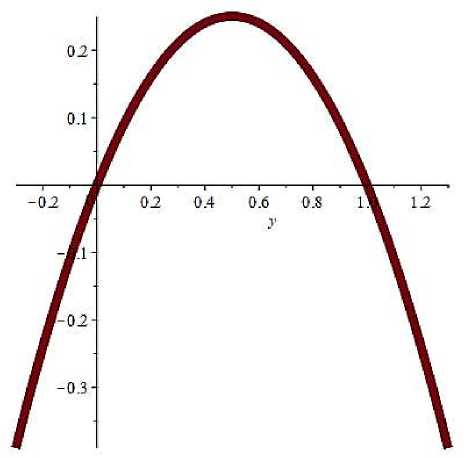
Если y ∈ (– ∞ ;0) ∪ (1;+ ∞ ), то y '( t )<0; а если y ∈ (0;1), то y '( t )>0.

В системе Maple построим точное решение задачи Коши, а также ее график.

Для этого в системе Maple по следующему маршруту откроем окно ODE Analyzer

Assistant: Maple/Tools/Assistants/ODE Analyzer…

Вводим уравнение: diff(y(t),t)=y(t)*(1-y(t)); вводим начальное условие: у (0)= ε .

£ e-t+£-e-t£.

В результате получим точное решение: y(t)

Вводя конкретные значения для малого параметра построим график выше полученного точного решения:

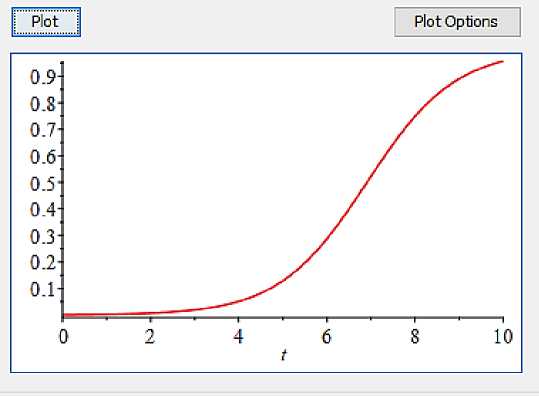
График точного решения при ε =0,001

В графике можно заметить скачок, т. е. резкое изменение решения задачи Коши [1–9]. Для определения точки скачка решения запишем точное решение в виде:

y(t) =

г

£ec

e^-t+£-e^-t£   1+г(е^с-1) .

Если 0 <   £(e^t — 1) = q < 1 или 0 < t < ln( 1 + £ ¹ ), то для решения задачи Коши (1)(2) получим следующее разложение:

y(t) = i+q = £e ^{t (} 1 — q + q ² — q ³ +—+(—q) ⁿ +—)

Точнее

y(t) =

_1+££et__1} = £e ^{t (1} — £(e ^f — 1) + £²(e^t — 1) ² — ■ ■ +(—£) ⁿ (e ^f — 1) ⁿ +■ ■ ■).

А если ln( 1 + £ ¹ ) < t, то решение y ( t ) можно записать в виде:

y(t) =

г

e-t+£-e-

_ £бС q£   1+££Г-£

1+ 1-F

S6 ^L

ln( 1 + £ ¹ ) < t ^ 1 + £ ^{1 t} ^1 +

1+г

£ <  £e^t ^ — < 1.

Отсюда следует следующее неравенство:

Ч< ¹⁺ 7 < 1

г+с    г+с

1-г _

^ £+ ^ <

Окончательно, при ln( 1 + £ ¹ ) < t имеем:

y(t) = —1 1 + 1

-

£e

1 — = 1 —-■ £

t

-

£e ^f

£

- +

1 — £               1 — £ ^П

(let") —■■■ ^+(—1)nh e^ ⁾ +■■■

Таким образом нами доказана следующая теорема. Теорема. Решение задачи Коши (1)–

• (2)    в точке t = l и (1 + D имеет скачок и для этого решения справедливо асимптотическое разложение:

  у(0 = ^{

  
  

y1(t),0 < t < l n( 1 + £ 1), y2(t),ln(1 + £-1) < t, где y1(t) = £ef(1 — £(et — 1) + £2(et — 1)2—...+(—£)n(et — 1)n+„J,

y2(t) = 1 —-

-

££ ^f

£

- +

/1 — £2              1 — £ ^П

(те^) -■■■ ^+(—1)Пп е^) +■■■

На основе теории обыкновенных дифференциальных уравнений решение задачи Коши

(1)–(2) непрерывна при 0

(1+7)

значение

решения равна у = 1+⁷.

Следствие. Справедливы предельные равенства:

limy1(t) = 0,limy2(t) = 1. £^0          £^0