Нелинейно-упругая деформация подводного трубопровода в процессе укладки

Высокие стандарты безопасности подводных трубопроводов обуславливают актуальность математического моделирования их напряженно-деформированного состояния (НДС) [1–7]. Повреждение трубопровода может возникнуть уже в процессе его укладки с судна на дно. Расчет возникающего НДС с учетом различных факторов и нелинейностей — цель данного исследования. Линеаризованная задача поставлена и решена в [7].

Вследствие малости относительной толщины рассматриваемого участка трубопровода (порядка 10 - 3 ) можно использовать одномерные модели стержней как материальных линий Эйлера–Кирхгофа–Коссера [8–13]. Расчеты показали, что на свободном участке достаточно ограничиться использованием классической нелинейной модели без растяжения и сдвига, а на дне, при определении контактного давления, необходимо учитывать влияние поперечного сдвига [14]. Дно, как основание, считается горизонтальной плоскостью, жесткой и гладкой. Граница участка контакта устанавливается из соответствующих условий сопряжения. Для значительных глубин становится обязательным учет не только геометрической, но и физической нелинейности, поскольку бетон внешнего слоя трубопровода не подчиняется закону Гука. Особого внимания требует расчет гидростатической нагрузки на трубу. Встречающиеся упрощенные представления [2, 4, 5, 15] могут изменить решение и количественно, и качественно.

Предлагаемые в работе теория и методика расчета позволят оптимизировать процесс укладки подводных трубопроводов без перенапряжения на начальной стадии.

1.    Постановка задачи и система уравнений

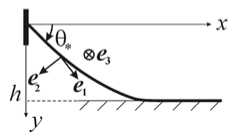
Трубопровод, представляющий собой двухслойную искривленную трубу из стали и бетона, моделируется полубесконечным стержнем, жестко закрепленным на левом конце (Рис. 1). Стержень, обладающий податливостью на изгиб, растяжение и сдвиг, нагружен собственным весом и внешним давлением жидкости. Расстояние h между закреплением и дном считается заданным; длина свободно провисающего участка l неизвестна и должна быть найдена. За отсчетную конфигурацию трубопровода принимается распрямленная форма стержня в ненапряженном состоянии.

Геометрическая форма стержня как материальной линии определяется зависимостью r ( 5 ) радиус-вектора r образующих эту линию точек от лагранжевой координаты 5 ; в начальном состоянии это r ₀ ( 5 ) .

а

б

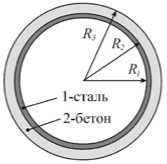
Рис. 1. Схема трубопровода ( а ) и его сечение ( б )

Поскольку 5 является дуговой координатой, то производная r₀' ( 5 ) равна орту касательной t ₀. В то же время с каждой частицей стержня как линии Коссера связана тройка ортов e i ( 5 ) ; в начальном состоянии обычно e i ₀ = t ₀ ( 5 ) . Вектор кривизны и кручения стержня Q ( 5 ) определяется равенствами e '= Q x e i . Тензор поворота P = e i e i ₀ (по повторяющимся индексам производится суммирование) связывает направляющие орты до и после деформации: e i = P ■ e i ₀.

Система уравнений нелинейной статики упругих стержней имеет вид [10, 11]

Q'+ q = 0,  M' + r'x Q + m = 0,

к = Q - P ■ Q ₀ = A ■ M + C ■ Q , Г = r '- P ■ r 0 = B ■ Q + M ■ C .

Здесь Q , M — векторы силы и момента в сечении с координатой s . Два первых уравнения описывают баланс сил и моментов при распределенных нагрузках q , m (силовой и моментной), другие соотношения вводят векторы деформации к , Г и связывают их с силовыми факторами посредством тензоров податливости A , B , C i . Вся система уравнений (1) может быть выведена из принципа виртуальной работы [10–13]. Соотношения упругости в (1) соответствуют физически линейной модели с квадратичной зависимостью энергии деформации П ( к i , Г i ) от своих аргументов. В случае физической нелинейности M = e i дП/дк i , Q = e i дП/дГ i , где к i = к e i , Г i = Г - e i , что также следует из принципа виртуальной работы.

Тензор А характеризует податливость на изгиб и кручение, тензор B — на растяжение и сдвиг, тензор C i выражает перекрестные связи. Вычисление тензоров податливости требует рассмотрения трехмерной модели стержня. При этом используются решения Сен-Венана, асимптотический метод и вариационный подход с аппроксимациями по сечению [10–13]. Простейшим вариантом представления тензоров является следующий: А = £ A i e i e i , B = ^ B i e i e i , C i = 0 ; здесь отличны от нуля шесть податливостей: на кручение — A ₁ ; на изгиб — A ₂ , A ₃ ; на растяжение — B ₁ ; на сдвиг — B ₂ , B ₃ .

Далее рассмотрим деформацию трубопровода в вертикальной плоскости xy при m = 0 с простейшим вариантом тензоров податливости. В плоскости xy (Рис. 1, а ) лежат векторы Q , q , r , Γ , e ₁ , e ₂ . Перпендикулярны плоскости (то есть параллельны декартовой оси z с ортом k = e ₃) векторы M , к . Вместо тензора поворота достаточно взять 9 ( 5 ) — угол между осью x и ортом e 1 . С учетом сделанных допущений уравнения (1) упрощаются: Q ' + q = 0, M ' + k ■ r ' x Q = 0, 0 ' = AM , ( A = A 3 , M = A '9' = A ^-1к ), r ' = e 1 + B ■ Q , e 1 = i cos0 + j sinO, B = B 1 e 1 e 1 + B 2 e 2 e 2 , e ₂ =- i sin0 + j cos0. В проекциях на декартовы оси x , y имеем систему

Qx+ qx = 0, Qy+ qy = 0, M' + x'Qy -y'Qx = 0, 9' = AM, x' = cos 9 + BQ + BxyQy, У' = sin 9 + BO + BQ,

xx x xy y                        yx x yy y

B_Tx = B , cos² 9 + B , sin² 9 ,   B,„ = B. sin² 9 + B , cos² 9 ,   B =( B. - B ,) sin 9 cos 9 .

xx 1          2            yy 1          2            xy 12

2.    Контактная задача с упрощенной нагрузкой

Сначала полагаем, что гидростатическая нагрузка постоянна. Тогда

A * (0,          5 <  1 ,

qx = 0, qy = w + {-p (5 ) , 5 > 1,

где w = const — погонный вес трубопровода в воде [15]. Контактное давление p ( 5 ) и координата 5 = 1 конца свободного (провисающего) участка не известны. Очевидно, что в системе уравнений (2) Q x = 0 .

На участке контакта имеем y ^ h ^ sin 9 + B yy Q y = 0 ^ Q y =- sin 9/ B yy ; p = w + Q y ; М ' + x’Q_y = 0 ^ 9" + A ( cos 9 + B xy Q y ) Q_y = 0 ^9" = ( AB ₂/ B yy ) sin 9 cos 9 . Здесь уравнение для 9 ( 5 ) допускает понижение порядка до первого:

9’ 2 + AB 2/ [ ( B i - B 2 ) B yy ] = const = A /( B - B 2 ) ^ 9' = - JA/b; sin 9 j          (3)

при этом используется условие 9 ( » ) = 0.

Уравнение (3) может быть проинтегрировано в квадратурах, но более простым является его численное интегрирование. В начале контактного участка

9 = 9 , ,   М = М , ^ - sin 9      AB . ( 9 , ) ,   Q y = Q y, ^ - sin 9 ,/ B   ( 9 , ) .                   (4)

Угол 9, — одна из неизвестных величин рассматриваемой контактной задачи.

На свободном участке выполняется условие Q_y = Q_{y 0} - w5 ( Q_{y 0} = const). Тогда из (2) получается система обыкновенных дифференциальных уравнений (ОДУ) для М , 9 , x , y ; ее общее решение содержит четыре произвольных константы. Граничные условия имеют вид: в заделке (при 5 = 0) — x = y = 0, 9 = 9 , ( 9 , — заданный угол закрепления); на конце свободного участка (при 5 = I ) — условия (4) и y = h . Итого, для отыскания семи неизвестных (среди которых Q_{y 0}, l , 9,) задается семь граничных условий.

При введении новой координаты ^ = I - 1 5 е ( 0,1 ) и записи разрешающих уравнений и граничных условий с ее использованием задача может быть решена численно методом конечных разностей. Для этого стержень делится на N отрезков с равномерным шагом 5 = 1/N . Дифференциальные уравнения и граничные условия записываются в разностном виде; функциям М , 9 , x , y непрерывного аргумента £ ставятся в соответствие сеточные функции M i , 9 i , x, , y i ( i = 0,..., N ). По найденным приближенным значениям функций в узлах затем посредством интерполяции восстанавливаются сами функции [18–21].

Система ОДУ задачи представляется в операторном виде: dY/d £ = G ( £ , 1 , Y ) , где функция Y = ( М , 9 , x , y ) T . Для аппроксимации системы используется неявная симметричная одношаговая разностная схема, имеющая второй порядок точности [18, 20, 21]: ( У, _{+ 1} - У, )/ 5 = ( G i + G_{i + 1} )/2, ( i = 0,..., N - 1). В результате преобразований получается система 4 N разностных нелинейных алгебраических уравнений. Общее количество неизвестных задачи складывается из значений четырех искомых функций в узлах 4 ( N + 1 ) и трех дополнительных неизвестных Q_{y 0}, 1 , 9 ₁ . Система уравнений дополняется разностными аналогами семи граничных условий: x ₀ = y ₀ = 0, 9 ₀ =9 , , y_N = h , 9 _N =9 ₁ , M_N = М , , Q_{y 0} = Q_y1 + w . Далее применяется итерационный метод Ньютона [18, 19, 21], начальным приближением служит решение линейной задачи для стержневой модели в классической постановке.

Изложенный алгоритм был реализован в пакете MATHEMATICA. Также задача решалась методом стрельбы в пакете MATHCAD (с использованием встроенных функций “sbval” и “rkfixed”). Результаты вычислений совпали.

Расчеты проводились для трубопровода, сечение которого образуют два кольца, внутреннее стальное и внешнее бетонное, с радиусами R 1 = 0,565 м, R ₂ = 0,6 м, R ₃ = 0,7 м (Рис. 1, б) . Эти (и следующие) параметры соответствуют реальному трубопроводу компании Nord Stream [17]. Сталь имеет модуль упругости E 1 = 210 ГПа, коэффициент Пуассона V 1 = 0,28, объемную плотность р 1 = 7800 кг/м³. В данном расчете бетон считается физически линейным материалом со свойствами: E ₂ = 27,5 ГПа, v ₂ = 0,2, р ₂ = 2450 кг/м³ [16]. Плотность морской воды составляет р H = 1028 кг/м³.

При определении жесткостей трубопровода как составного стержня считалось, что стальной и бетонный слои работают параллельно, и потому их жесткости складываются:

A-1 = £ EnIn, B- = £ EnSn, B2-1 = K £цnSn ,(5) n =1,2                       n=1,2                           n=1, где площади кольцевых поперечных сечений, их моменты инерции и модули сдвига вычисляются по формулам: Sn - n(Rt -Rn), In - n(R4+1 -R4)/4, Цn - En/[2 (1 + vn)]. Здесь n = 1, 2 (индекс 1 относится к стали, 2 — к бетону), K = 0,5 — коэффициент сдвига для тонкого кольца, который обуславливается геометрической формой сечения; значение коэффициента установлено в результате исследования краевых задач, проведенного в работе [12].

Расчет позволил оценить влияние растяжения и

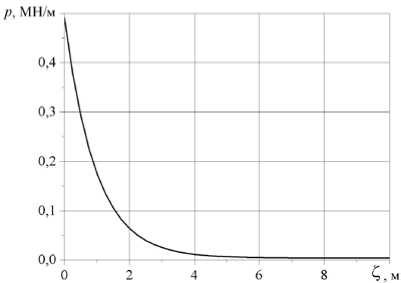
Рис. 2. Распределение контактного давления ( Z = 5 - l )

сдвига. Сравнение полученных результатов с результатами по модели Кирхгофа показало, что роль

растяжения ничтожна и, следовательно, податливостью B1 можно пренебречь. Влияние сдвига невелико на свободном участке трубопровода: так координата точки контакта в модели Кирхгофа x(l) = 265,4 м, а в модели со сдвигом — 264,5 м; значения силы в сечении, отвечающие этим моделям, отличаются на доли процента. Но сдвиг заметно влияет на контактное давление (Рис. 2) — оно сводится к сосредоточенной силе при B2 ^ 0. Влияние сдвига на изгибающий момент показано на рисунке 3 для случая, когда глубина и угол закрепления составляют: h = 100 м, 9, = 30°. Как видно из графиков, расхождение моментов мало,

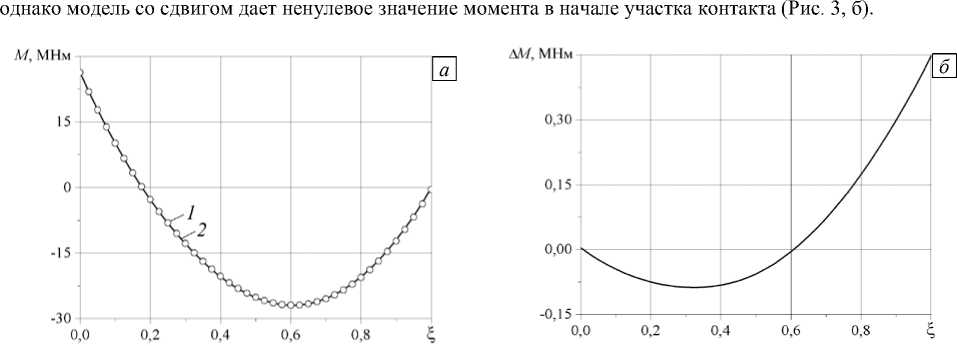
Рис. 3. Сравнение значений изгибающего момента, вычисленных по двум моделям ( а ): модель Кирхгофа (кривая 1 ) и модель со сдвигом ( 2 ); разность этих моментов ( б )

Далее решается задача с B = 0 (то есть задача для стержневой модели в классической постановке). С помощью этой, более простой, модели изучается влияние угла 9 , на НДС, при этом используется точное выражение гидростатической нагрузки.

3.    Гидростатическая нагрузка

Рассмотрим провисающую часть трубопровода как трубку с осью L и сечением F (Рис. 4).

Радиус-вектор точек на оси r = r (5) — функция дуговой координаты. Орт j направлен по оси у вертикально вниз (как и выше). Давление в произвольной точке поверхности трубки, имеющей радиус-вектор R , равно p = p0 + yj ■ R, где p0 — давление при у = 0 (Рис. 1), у = рHg — удельный вес воды.

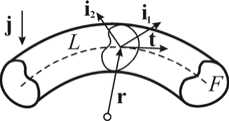
Рис. 4. Трубка в воде

На отрезок трубки 51 < 5 < 52 действуют гидростатические силы с главным вектором s2

- J p N dO = J q H d5 .

Os ₁

Здесь O — боковая поверхность, N — орт внешней нормали к ней; выражение гидростатической нагрузки на единицу длины трубки q _H предстоит вывести.

Вектор площадки N dO определим известными средствами дифференциальной геометрии.

В каждом сечении s = const введем декартовы оси x _а с ортами i _а . На контуре д F сечения имеем x _а = x _а ( ю ) — функции дуговой координаты. Поверхность трубки задается зависимостью радиус-вектора от двух координат R ( ю , s ) = r ( s ) + x , x = x „ ( ю ) i _a ( s ) . По касательным к координатным линиям ( ю , s )

Д дR    , / X . Д            Д dR        О направлены векторы производных   Rю =— = x1юу ia = т,    Rs = — = t + Q x x