Нелинейное развитие структур в экмановском слое

В последние десятилетия особое внимание привлекают проблемы развития в атмосферном пограничном слое (АПС) вследствие гидродинамических неустойчивостей различных когерентных

структур, в частности, широко распространенных упорядоченных спиралевидных вихрей с горизонтальной осью. Эти квазидвумерные структуры, сравнимые по масштабам с высотой пограничного слоя, имеют множество названий: квазипараллельные валиковые структуры, вихри в виде валов, продольные валы, спиралеобразные вихри, продольные вихри, двумерные горизонтальные вихри, вторичная циркуляция, линейная конвекция, двумерная конвекция, валы, роллы и другие.

Валиковые структуры образуются уже при довольно слабом ветре (2÷3,5 м/с) [1], когда происходит перестройка трехмерных конвективных ячеек в продольно ориентированные, и отчетливо визуализируются в виде так называемых «облачных улиц», хорошо заметных на спутниковых снимках [2] и изображениях, полученных с использованием радаров с синтезированной апертурой — Synthetic-Aperture Radar (SAR), позволяющих составлять карты поверхностных ветров с разрешением 1 км и достаточной степенью точности [3]. Наблюдаются они в близких к нейтральным условиях и при устойчивой/слабонеустойчивой стратификации пограничного слоя. Такие структуры характерны для высоких широт, где над более теплой водной поверхностью в результате вторжений холодного воздуха создаются условия для конвекции, которая в сочетании с ветром формирует устойчивую систему вытянутых горизонтальных валов, существующих на протяжении многих дней [3–6]. Валы имеют горизонтальные масштабы порядка 3÷5 км (поперек вала) [1], угол между продольной осью валов и направлением геострофического ветра обычно не превышает 30°. Похожие продольные вихри присущи и пограничному слою сформировавшегося тропического урагана, после прохождения которого поверхностные образования и разрушения имеют полосчатую структуру [3, 7, 8, 9, 10, 11].

Долгоживущие спиралевидные вихри значительно влияют на характеристики турбулентного течения, определяют вертикальный профиль среднего течения, играют существенную роль в процессах перемешивания, в процессах переноса влаги, тепла и других субстанций через АПС. По оценкам, сделанным в [7, 12], вторичные потоки воздуха в виде валиковых структур отвечают за 20÷60% всего тепломассопереноса через АПС. Данные о пространственных масштабах и других характеристиках когерентных структур в нижней части этого слоя необходимы для успешного прогнозирования различных погодных явлений.

Возникновение и существование крупномасштабных когерентных структур являются следствием развития в АПС таких гидродинамических неустойчивостей, как динамическая — неустойчивость, связанная с наличием точки перегиба на профиле агеострофической компоненты скорости ветра [13, 14], «параллельная» [14] (иногда ее считают частным случаем динамической неустойчивости; потеря неустойчивости при этом не зависит от наличия точки перегиба, а происходит за счет связи между горизонтальными компонентами скорости ветра) и конвективная [15, 16]. В большинстве случаев, согласно [17], создаются условия для действия динамической или конвективной неустойчивости, влияние «параллельной» неустойчивости значительно меньше.

Модель с конвективной неустойчивостью позволяет получить продольные вихри, ориентированные в направлении геострофического ветра. Однако наблюдаемые периоды валиков и соотношение их горизонтальных и вертикальных масштабов оказываются нередко много большими предсказанных теоретически. Существующие теории сталкиваются с трудностями в определении амплитудных характеристик когерентных структур в АПС.

В [14–16] проведен линейный анализ устойчивости нейтрального АПС для периодических по поперечной координате возмущений. В [18–20] развиты слабонелинейные теории. В настоящей работе осуществляется анализ нелинейной задачи в диапазоне чисел Рейнольдса от 100 до 400. Исследование в близкой постановке содержится в [21]. В [22] рассматривается образование когерентных структур над однородным лесным пологом вследствие неустойчивости Кельвина-Гельмгольца и процесс переноса пассивной примеси из полога в атмосферу. В [23] описано влияние влажности и температуры на генерацию вихревых структур в нижнем слое атмосферы на основе двумерной модели мезомасштабных процессов. В [10, 11] численно моделировались продольные вихри в пограничном слое сформировавшегося тропического урагана, возникающие в условиях динамической и конвективной неустойчивости.

Как сами крупномасштабные течения, структура которых обуславливается совместным действием турбулентного трения и силы Кориолиса, так и турбулентные движения в АПС обладают ненулевой спиральностью, которая вычисляется как скалярное произведение поля скорости и завихренности [24–27]. Турбулентные каскады спиральности в АПС обнаружены в натурных экспериментах Института физики атмосферы им. А.М. Обухова РАН [28, 29] и в недавних результатах прямого численного (DNS) моделирования [30–32].

Отметим, что в [31, 32] так же, как и при численном моделировании полной системы уравнений для пограничного слоя атмосферы в рамках вихреразрешающей (LES) модели, например в [33], явная картина валиковой циркуляции не воспроизводилась, что отчасти связано с недостаточной детализацией сетки в расчетной области и трудностью точного «попадания» на неустойчивые моды, а также неустойчивостью когерентных структур по отношению к трехмерным возмущениям [9]. Структуры в этом случае могут наблюдаться какое-то время, но в силу неустойчивого состояния системы в целом находятся в условиях постоянного чередования процессов формирования и разрушения, что осложняет их анализ [21]. Тогда как квазидвумерные численные модели мезомасштабных процессов являются полезной основой для гидродинамических исследований и активно использовались и используются при разработке нелинейных теорий, в аналитических изысканиях, оценках влияния различных типов неустойчивостей на характеристики мезомасштабной конвекции [2, 9, 13, 19, 34], анализе устойчивости полученных решений [14]. Такие модели, в отличие от прямого численного моделирования, где небольшие трехмерные возмущения приводят к неустойчивости и разрушению спиралевидных вихрей, и от LES моделирования, где редко хорошо воспроизводятся роллы и разрешаются только короткоживущие мелкомасштабные, расположенные близко к земле стрики [35, 36, 37], стабильно демонстрируют появление продольных вихрей и позволяют сфокусироваться непосредственно на изучении параметров когерентных структур без учета влияния ошибок и неоднозначностей при выборе их различных параметризаций, погрешностей подсеточного моделирования, возникновения других типов когерентных структур (например, стриков). Устойчивость получающихся квазистационарных решений по отношению к дву- и трехмерным возмущениям до сих пор остается малоизученной [21].

В [38] проверялось влияние на устойчивость экмановского пограничного слоя тензора турбулентных напряжений, учитывающего присутствие турбулентной спиральности. Спиральность существенно сказывается на возмущениях, характеризуемых динамической неустойчивостью. При этом меняется как критическое число Рейнольдса, так и параметры вторичных возмущений: волновые числа и углы ориентации валов по отношению к направлению геострофического ветра. В [39] исследовалось развитие валиковой циркуляции в температурно-стратифицированном АПС на основе модели турбулентности [40], учитывающей турбулентную спиральность.

Помимо параметризации спиральности в моделях АПС важным вопросом остается приемлемость принятого допущения о постоянстве турбулентной вязкости. В настоящей работе проводится сравнение результатов моделирования и практических наблюдений. Для оценок используются полуэмпирические значения турбулентной вязкости, полученные на основе экспериментальных данных о турбулентных характеристиках в АПС [27].

Размеры расчетной области в значительной степени превышают размеры когерентных структур, что позволяет проанализировать поля мезомасштабной спиральности и взаимодействие различных типов неустойчивостей, а также проверить существование асимметрии структур внутри циркулирующих потоков.

2.    Основные уравнения

В настоящем исследовании рассматривается случай нейтральной стратификации. Ось X направлена вдоль оси валика, ось Y — перпендикулярно ей. Средние профили характеристик когерентных структур предполагаются независимыми от X .

Характеризуя мезомасштабную циркуляцию продольной скоростью по оси X и проекцией завихренности на ось X , описываем роллы в безразмерном виде системой уравнений:

Re

Re

д и .. д и д Т д U — + V — +--- д t    д у д у д z	д Т д и	д Т д и +- -	д Т д и\	д Т д и\ 1 +              1	= А и -	, дТ 2 дГ ’
	д z д у	д у д z \	д у д z /	\ д z д у / J
дф + V дф + д Т д У д t д у д у д z 2	д Т дф	д Т дф /	'д Т дф'	\ /дТ дф\'	)= Аф-	д и "2 & •
	д z д у	д у д z \	, д у д z,	/ \ д z д у /
		ф =-А Т ,
Л д 2     д 2 А = —2 +-- 2,   1 д у 2    д z 2	1 y max aа) =----- j а ( z ) dy , y max 0		v =	d Ψ --, w dz	= d Т dy

Здесь: u , v , w — продольная (направленная вдоль оси ролла), поперечная и вертикальная компоненты скорости ролла; Т — функция тока; ф — проекция завихренности на ось X ; ( а ) — оператор осреднения какой-либо функции а по координате у ; А — оператор Лапласа; Re — число Рейнольдса.

В качестве масштабов длины, скорости и времени выбраны, соответственно, толщина экмановского слоя D = ( К/ f ) 12 , скорость геострофического ветра G = ( U_G ² + V_G ² )^Z , T = D/G При этом К — коэффициент турбулентной вязкости; f = Qsin 9 — параметр Кориолиса, где Q — угловая скорость вращения Земли, 9 — широта; U_G и V_G — геострофическая и агеострофическая компоненты скорости ветра.

Составляющие скорости среднего течения U ( z ) и V ( z ) описываются уравнениями:

—

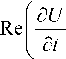
д т д и\ /д т д u\   a и I д² и

++ V1 =     + 2 (V — VG),

дz дy j \ дy дz     дy J   дz1    '

—

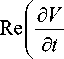
дт д2т\ /дта2т\    au | д2v , ч

++ V— 1 = —' 2 (U — VG), дz дyдz / \ дy дz2 /    дy J дz z

GD

Re =---

K

На верхней границе, z = H , а также в отсутствие роллов стационарное решение задается модифицированным экмановским профилем скорости:

U = cos (s) — exp (— H )■ cos (H + е),

V = — sin (s) + exp (— H )■ sin (H + s).

Здесь s — угол между осью роллов и направлением геострофического ветра. При моделировании угол выбирался в диапазоне от — 45 ° до 45 ° .

Влияние турбулентной спиральности в настоящем исследовании, в отличие от [38, 39], не рассматривается, поскольку ее учет, как правило, не приводит к качественному изменению явления мезомасштабных циркуляций, а в целом уменьшает эффективное число Рейнольдса.

3.    Описание численной реализации и вычислительного алгоритма

Записанная выше система уравнений решается конечно-разностным методом. Для аппроксимации уравнений переноса (1), (2) применяется явная схема с направленными против потока разностями. Схема обладает искусственной схемной вязкостью.

После приведения подобных членов получается разностный аналог модельного уравнения переноса, записанного с учетом конвективного и диффузионного членов [39]:

Ft + uFy + vFz =

К, UI I k+ 2 J F” +

k + h z 2 v l I F..

Здесь Fy и F- — аппроксимации первых пространственных производных для какой-либо функции F из искомых и, ф; Fyy, Fzz — аппроксимации вторых пространственных производных; hy, hz — шаги пространственной сетки по направлению X или Y соответственно; k — обобщенный коэффициент диффузии. Такая явная схема известна своим стабилизирующим влиянием на эффекты гидродинамической неустойчивости [41].

Используется ограничение на шаг по времени:

т <

4 к

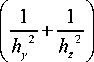
₊ И ₊ М' h y    h z J

Уравнение Пуассона для функции Ψ (3) решается с помощью итерационного метода последовательной верхней релаксации [42]. Для аппроксимации среднего течения в АПС применяется условно-устойчивая явная схема. Ограничение на шаг по времени следующее: т <  h z ²/ (4 к ).

Размер расчетной области по координате Y — L_y находится в пределах безразмерных величин 48÷144. Для достижения стационарного режима в некоторых случаях (при больших Re) он увеличивается. Количество узлов, как правило, не меняется, поскольку при одновременном с размером расчетной области его увеличении (при сохранении длины шага по координате Y ) общая временная динамика и результаты расчета слабо реагируют на этот параметр, лишь в интегральных характеристиках энергии и спиральности проявляются дополнительные детали осцилляций. Размер по координате Z — L_z равняется 12, что превышает высоту АПС, которая в среднем равна 5.

Код программы написан на языке Fortran. Время расчета зависит от выбранного числа Рейнольдса и угла ориентации роллов и длится от пары часов до нескольких суток. Количество шагов сетки по координате Y берется равным 241, по координате Z — 121. Шаг по времени составляет 0,00125.

Плотности энергии E и спиральности H валиковых структур определяются по формулам:

E =

2 L y L z

j ( u ² + T A T ) dydz ,

H = -2- J(- u AT) dydz.

L y L z

Для системы уравнений движения граничными условиями являются условия прилипания на нижней границе: при z = 0 имеем u = 0, w = 0, v = 0, и заданная геострофическая скорость при z ^^ .

d u             av

На верхней границе отсутствует трение: — = 0, w = 0, — = 0.

д z             д z

На боковых границах для функций u ,    ф ,   Т выполняются условия периодичности:

F ( t , y , z ) = F ( t , y + 1 , z ) . Завихренность на нижней границе при z = 0 вычисляется по формуле Тома [43]:

ф °’ ^у =^- 1г ^T i’ ^y ,^{где T1J}

— функция тока во внутренних узлах сетки.

Последовательность вычислений следующая:

• 1.    Задаются нулевые начальные значения для функций u, Т ; возмущение для ф в центре расчетной

• 2.    Определяются u, ф во внутренних узлах расчетной области.

• 3.    По известному ф на новом временном слое итерационным методом рассчитывается функция тока Т

• 4.    Вычисляются граничные значения ф на новом временном слое с использованием Т во внутренних узлах расчетной области.

• 5.    Отыскиваются характеристики среднего течения U(z), V(z).

• 6.    Осуществляется переход на следующий временной шаг.

4.    Результаты

области; начальные профили для скорости среднего течения, соответствующие модифицированному экмановскому профилю скорости.

во внутренних узлах расчетной области.

Типичная толщина экмановского пограничного слоя D находится в пределах от 100 до 500 м, поэтому, в соответствии с выражением Re = GD/K , типичный диапазон изменения числа Re — от 100 до 1000. Особенный интерес представляет диапазон его низких и средних значений. Кроме того, анализ нелинейной теории для больших Re затруднен, так как с повышением значений чисел Рейнольдса решение аппроксимированных предложенным в данной работе методом уравнений становится все более неустойчивым, а получающиеся валики увеличиваются в размерах по горизонтали (см., например, Рис. 1–3). Последнее обстоятельство приводит при численном моделировании к уменьшению количества роллов в расчетной области, что, вероятно, и является одной из причин неустойчивости решения системы уравнений. Полученные квазистационарные валики перемещаются в направлении, перпендикулярном оси валиков (слева направо на Рис. 1–3). В случае заметной асимметрии и наличия структур больших размеров происходят изменения диаметров малых валиков с небольшой амплитудой. В среднем интегральная энергия структур не изменяется.

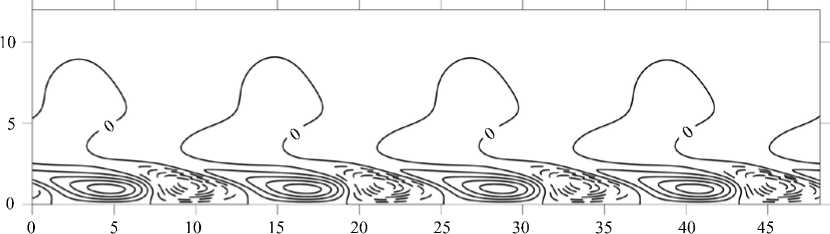
Рис. 1. Пространственное распределение продольной компоненты скорости U по осям Y , Z при Re = 175, £« 15 ° и интервале между контурами 0,02; отрицательные значения показаны пунктирной линией

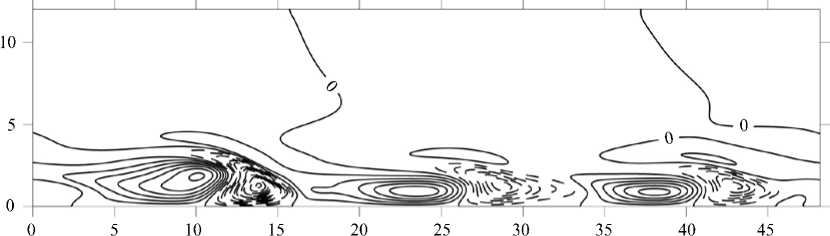
Рис. 2. Пространственное распределение продольной компоненты скорости U по осям Y , Z при Re = 225, б- 10 ° и интервале между контурами 0,02; отрицательные значения показаны пунктирной линией

Рис. 3. Пространственное распределение продольной компоненты скорости U по осям Y , Z при Re = 300, б- 10 ° и интервале между контурами 0,05; отрицательные значения показаны пунктирной линией

Вплоть до значений Re ® 400 поля скорости, спиральности, энергии, завихренности и других параметров, характеризующих квазипараллельные валиковые структуры, вычислялись до момента установления стационарного режима. Предварительно выбирались число Рейнольдса и углы ориентации роллов. Угол изменялся в пределах от - 45 ° до 45 ° . Далее анализировались расчетные данные и определялся угол ориентации, при котором плотности энергии валиков достигали максимальных значений. Процедура вычислений повторялась для каждого числа Рейнольдса из анализируемого диапазона.

Известно, [34], что для слабонелинейной теории без учета силы Кориолиса в уравнениях движения и при отсутствии бароклинности при Re ® 54 начинает проявляться «параллельная» неустойчивость. Данная мода повернута на угол б ® - 15 ° . При увеличении Re более интенсивно развивается динамическая неустойчивость, и уже при Re ® 113 она превалирует над «параллельной». Угол ориентации б составляет в этом случае ~ 10 °^ 15 ° .

При решении по квазидвумерной численной модели получились близкие к найденным в рамках линейной устойчивости значениям величины углов ориентации (см. Табл. 1), а числа Рейнольдса порядка Re ® 150 оказались соответствующими точке перехода от одного типа неустойчивости к другому.

Таблица 1. Значения угла ориентации роллов с максимальной энергией при различных числах Рейнольдса

Re	100	115	125	150	175	200	225	250	300	350	400
б , °	–15	–10	–10	15	15	15	10	5	10	5	5

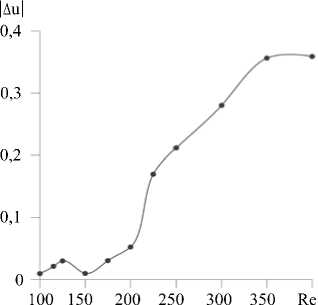
Рис. 4. Зависимость асимметрии продольной составляющей скорости от числа Рейнольдса

Крейчнан отмечал [44], что взаимодействие спиральных течений одинакового знака доминирует над взаимодействием спиральных течений разных знаков. Вследствие этого должна сохраняться зеркальная асимметрия, изначально связанная со спиральностью экмановского течения. Действительно, имеет место рост асимметрии продольного поля скорости. Асимметрия продольной компоненты скорости наблюдалась (без обсуждения) в [21]. На рисунке 4 показана разность амплитуд максимальных положительных и отрицательных значений продольной компоненты скорости в ролле. Она, как и амплитуда отрицательного по отношению к направлению геострофического ветра возмущения скорости, растет на отрезках от Re = 100 до Re = 125 и от Re = 150 до Re = 400. Между Re = 125 и Re = 150 происходит смена режима реализующейся

Таблица 2. Характеристики продольных вихрей и возможный разброс этих значений при неоднородном пространственном распределении валиковых структур на больших числах Рейнольдса

Число Рейнольдса Re 200 225 250 300 350 400 Асимметрия продольной компоненты скорости | Аи\ 0,0525 0,1698 0,2117 0,2802 0,2822 0,3189 Разброс S Аu –0,0145 –0,1410 –0,1758 –0,2292 –0,2322 –0,1940 Период валиков L 5,0 5,0 5,0 5,0 6,0 7,0 Разброс S |Z 0 -1,0 ^+1,0 -1,0 ^+1,0 -1,0 ^+2,0 -1,0 ^+1,0 -2,0 ^+2,0 Амплитуда положительной составляющей спиральности H+max 0,0139 0,0554 0,1073 0,1562 0,1582 0,1643 Разброс S|H + max| –0,0073 –0,0441 –0,0869 –0,0326 –0,1364 0,1214 Амплитуда отрицательной составляющей спиральности H_max| 0,0032 0,0056 0,0164 0,0263 0,0285 0,0363 Разброс S|H — max –0,0011 –0,0021 –0,0108 –0,0111 –0,0141 –0,0200 неустойчивости. При больших Re асимметрия вихревых структур становится отчетливой, что соотносится с распределением продольной составляющей скорости для Re = 300 (Рис. 3). Верхняя граница вихрей поднимается от z ~ 3 для Re = 175 до z ® 6 для Re = 300 (Рис. 1-3).

Возможный разброс значений при оценке асимметрии для пар валиков при больших Re представлен в таблице 2. Графики (см. Рис. 4, 6, 10) построены для случаев с максимальной асимметрией.

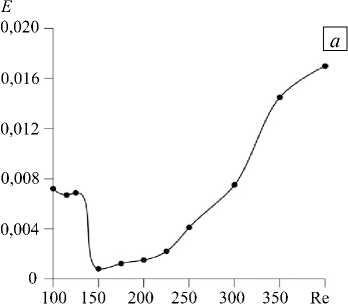
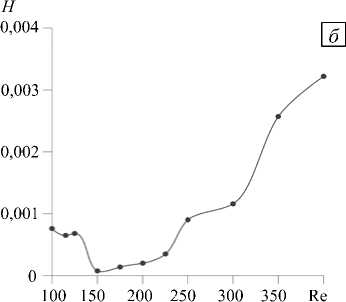
Рис. 5. Зависимости плотностей энергии E ( а ) и спиральности H ( б ) валиковых структур от числа Рейнольдса

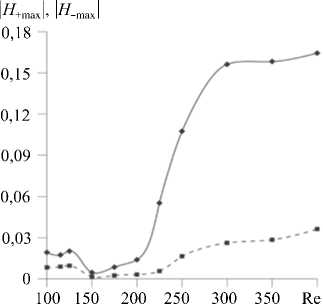
Рис. 6.

Изменение амплитуд положительной

(сплошная линия) и отрицательной (пунктир) составляющих спиральности в зависимости от числа Рейнольдса

После установления неустойчивости динамического типа с увеличением числа Рейнольдса возрастают плотности энергии и спиральности когерентных структур (Рис. 5). В целом спиральность в расчетной области положительна, что характерно для экмановского течения, для которого, в частности, интегральная по слою спиральность будет следующей [25]:

H in = J 0 " H ( z ) dz = 1/2( U g ² + V g ² ) > 0 .

Рассматривая спиральность каждого ролла по отдельности, можно выделить второй тип асимметрии — асимметрию спиральности. На рисунке 6 показано изменение амплитуд положительной и отрицательной составляющих спиральности как функций числа Рейнольдса. Разброс значений амплитуд спиральности представлен в таблице 2.

Наблюдаемое развитие асимметрии имеет, по всей видимости, черты, похожие на те, которыми обладает хорошо известное в лаборатории и геофизических системах явление циклон-антициклонной асимметрии (в системах с вращением более интенсивными и долгоживущими оказываются образования с антициклоническим вращением [45]). В обсуждаемом здесь случае в роли основного вихря выступает завихренность экмановского течения. Следует также иметь в виду известное стабилизирующее влияние восточного и дестабилизирующее влияние западного ветров на валиковую циркуляцию [21].

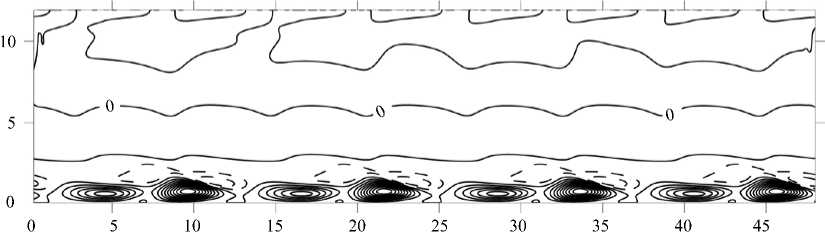
Рис. 7. Пространственное распределение спиральности H по осям Y , Z при Re = 175, £ = 15 ° и интервале между контурами 0,001; отрицательные значения показаны пунктирной линией

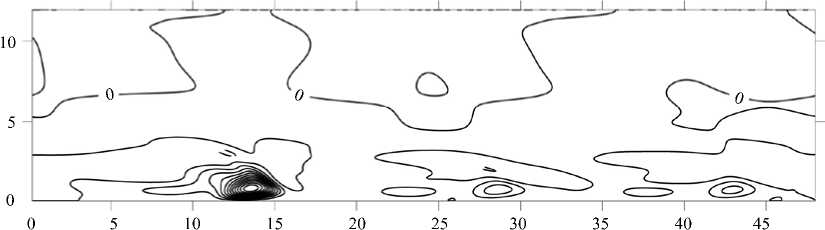
Рис. 8. Пространственное распределение спиральности H по осям Y , Z при Re = 225 , £ = 10 ° и интервале между контурами 0,005; отрицательные значения показаны пунктирной линией

Рис. 9. Пространственное распределение спиральности H по осям Y , Z при Re = 300, £ = 10 ° и интервале между контурами 0,01; отрицательные значения показаны пунктирной линией

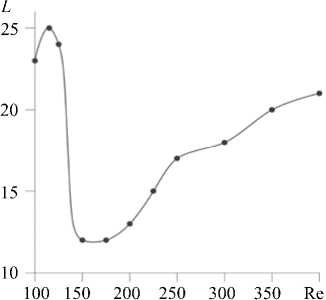
Рис. 10. Зависимость расстояния между валиками с противоположными знаками продольной скорости по направлению оси Y (полупериод) от числа Рейнольдса

На рисунках 7–9 изображены пространственные распределения спиральности для трех значений числа Рейнольдса. Хорошо видно, что при его увеличении асимметрия нарастает.

Расстояние по оси Y между валиками с противоположными знаками циркуляции также увеличивается при изменении Re от 150 до 400 (Рис. 10). Разброс значений при больших Re показан в таблице 2. При сильной нелинейности нарушается пространственная периодичность вторичных когерентных образований и становится возможным формирование структур, близких к уединенным. Подобные многомасштабные структуры фиксировались в течении типа Экмана–Куэтта [46, 47] в теоретических исследованиях [48] и в лабораторных экспериментах [49].

Для оценки величины асимметрии валиковых структур в АПС рассмотрим результаты акустического атмосферного зондирования с помощью ветровых профилемеров — содаров в Калмыкии в июле 2007 года

[1]. На рисунке 11 приведены спутниковые снимки этого же района от 28 июля 2007 года. В 14:03 по московскому времени наблюдается развитая мезомасштабная циркуляция (точкой 1 на рисунке обозначено место, из которого осуществляются измерения), угол отклонения валов от направления восток–запад равняется 35°. Геострофический ветер направлен на восток–юго-восток. Пространственный период видимых облачных улиц меняется в диапазоне 4÷7 км.

Эта картина воспроизводится в рамках мезомасштабной атмосферной модели RAMS [50]. Численное моделирование является широко практикуемым подходом и позволяет качественно оценить параметры возникающих структур и сравнить их со спутниковыми снимками и данными акустического зондирования. Вся расчетная область 300 на 225 км покрывается сеткой из 600×450 узлов с шагом по горизонтали 500 м. По вертикали сетка имеет 30 уровней до высоты 20000 м со сгущением в пограничном слое. В качестве

Рис. 11. Облачные улицы над районом содарных измерений; снимок произведен спутниковой системой MODIS-AQUA 28 июля 2007 г. в 14:03 (время московское)

начальных и граничных данных используются поля реанализа (поля метеорологических данных в узлах регулярной сетки за истекшие годы) NCAR — Национального центра атмосферных исследований США. Расчет начинался за сутки до изучаемого момента времени. На рисунке 12 показана изоповерхность вертикальной компоненты скорости ветра W = 1 м/с в окрестности точки 1. Исследуемая область имеет размеры 96 на 96 км по горизонтали и 3 км по высоте.

На рисунке 13 представлены изолинии вертикальной компоненты скорости ветра в пограничном слое в сечении, перпендикулярном оси роллов. При сравнении с рисунком 11 видно их неплохое соответствие пространственным распределениям циркуляционных движений, центры которых, согласно результатам моделирования, расположены примерно на высотах 1200÷1300 м.

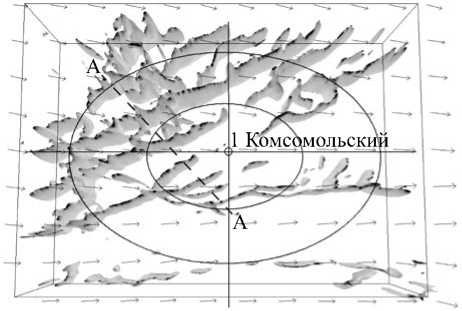
Рис. 12. Изоповерхности вертикальной компоненты скорости ветра W = 1 м/с (концентрические окружности радиусами 24 и 48 км) на высоте 3 км от земной поверхности) – модель RAMS по данным от 28 июля 2007 г., 14:03 (по московскому времени); стрелки показывают направление геострофического ветра на высоте 3,5 км, пунктирная линия A–A задает положение плоскости, в которой далее строятся изолинии вертикальной скорости W

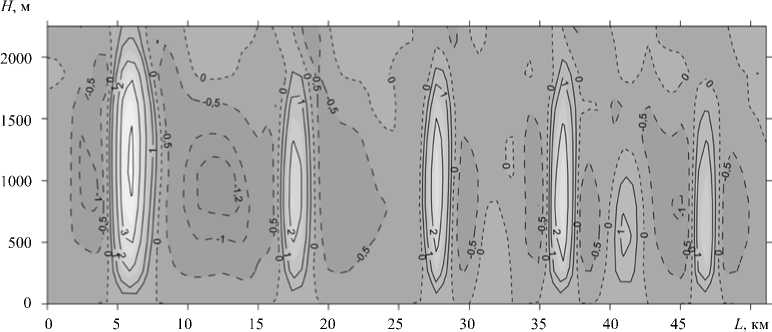
Рис. 13. Изолинии вертикальной скорости W в плоскости A–A рисунка 12, перпендикулярной оси роллов; размер валиков поперек их оси 3÷5 км (модель RAMS)

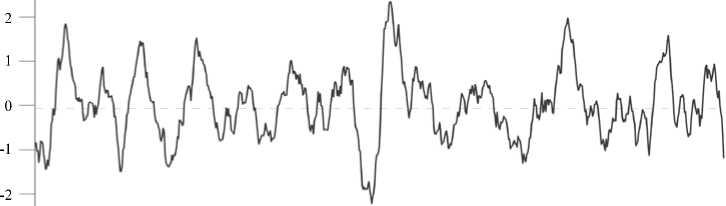
Однако разрешение, которым обладает модель, не позволяет рассмотреть особенности в распределениях физических величин. Для более детального исследования необходимо прибегнуть к вихреразрешающему моделированию. Для анализа воспользуемся результатами акустического зондирования из [1], согласно которым точность определения скоростей содаром составляет 0,5 м/с для горизонтальной компоненты и 0,2 м/с для вертикальной. Эти же значения являются пороговыми: содар регистрирует движения, начиная с них. На рисунке 14 приведен временной ход продольной скорости вдоль

U, м/с з —

-3

12                13                 14                15                 16                17             Г, час

Рис. 14. Временной ход направленной вдоль валика скорости, U , м/с в привязке к московскому времени T (данные содарных измерений на высоте 690 м от 28 июля 2007 г., Калмыкия)

валика по данным акустического зондирования на высоте 690 м c 12 до 18 часов московского времени 28.07.2007. Здесь представлено 10-минутное усреднение за вычетом 30-минутного среднего значения данных длинноволнового содара с вертикальным разрешением 30 м и временным 30 с. Максимальная высота зондирования не превышает 870 м. Подобная процедура позволяет отфильтровать флуктуационную составляющую и средний ход скорости ветра [1].

На рисунке 15 приводится высотно-временная развертка продольной скорости вдоль валика. Здесь также применена процедура 10-минутного усреднения за вычетом 30-минутного среднего. Хорошо видно, что преобладают области с отрицательными значениями продольной скорости, направленной примерно против направления геострофического ветра (в выбранной системе отсчета).

L

U, м/с

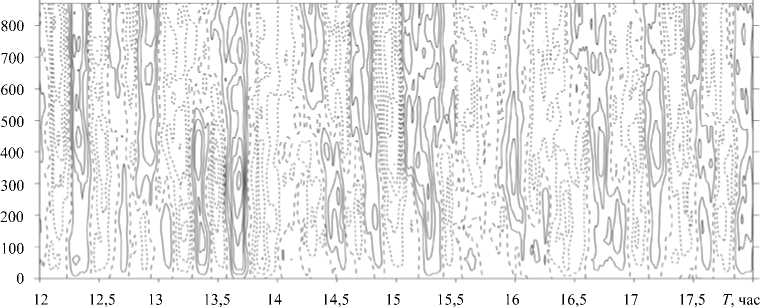
Рис. 15. Временной ход направленной вдоль валиков скорости U , м/с по данным содарных измерений 28 июля 2007 г. в Калмыкии на высотах 0-870 м с шагом 30 м; время по оси абсцисс московское; пунктиром отмечены отрицательные значения скорости, диапазон изменений от –3 до +3 м/с с шагом 0,5 м/с

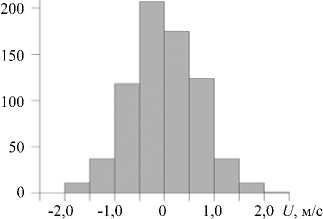
Рис. 16. Гистограмма распределений средней по высоте компоненты скорости, направленной вдоль валиков: по оси абсцисс – данные содарных измерений на высотах 0^870 м с шагом 30 м в диапазоне 12:00 ^ 18:00 час по московскому времени 28 июля 2007 г.

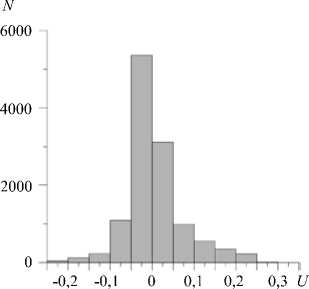
Рис. 17. Гистограмма распределений значений продольной компоненты скорости (безразмерной) в пределах высоты пограничного слоя; ось абсцисс – расчетные данные при Re = 300

На рисунке 16 представлено распределение средней по высоте слоя (по 29 уровням в слое 0÷870 м) продольной скорости вдоль валиков. Наблюдается заметная асимметрия ее отрицательных (против направления геострофического ветра) значений. Похожие распределения получаются и для большинства уровней зондирования. Дополнительно заметим, что асимметрия продольной компоненты скорости имеет место и в мезомасштабном моделировании на высотах 1000÷1300 м. Для качественного сравнения результатов двухмасштабной модели и натурных измерений на рисунке 17 приведена гистограмма распределений значений продольной компоненты скорости в пределах высоты пограничного слоя на основе расчетных данных для Re = 300 .

Определим для рассматриваемого случая эффективное число Рейнольдса. Рисунок 18 содержит профиль коэффициента турбулентной вязкости, полученный путем мезомасштабного моделирования в представлении вихревой вязкости (по значениям вертикального градиента средней горизонтальной скорости ветра) [27, 35, 37, 51]. Существуют различные подходы к восстановлению профиля этого параметра, в частности, представленный в [51] и используемый здесь для оценки эффективного Re :

K = l ² s ,   где s ²

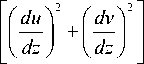
а l ' k z ^z ( 1 + Kzf /( 0,00027 G ) ) ].

Вертикальный размер роллов составляет, как правило, от 0,9 до 2,1 км [34]. Коэффициент турбулентной вязкости для выбранного момента времени осредняем до высоты примерно 2500 м (см. Рис. 18). Получаем среднее значение K « 54 м²/с. Такие значения характерны для неустойчивой стратификации.

С определенной степенью точности компоненты геострофической скорости ветра при содарных измерениях можно принять равными компонентам скорости на верхних уровнях зондирования, которые для исследуемого случая располагаются на высоте 870 м [52]. При этом компоненты геострофической

Z, км

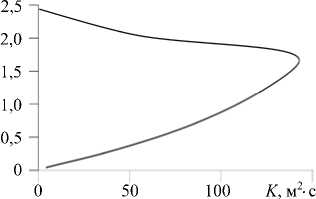
Рис. 18. Зависимость коэффициента турбулентной вязкости K (м²/с), от высоты z , км (по данным от 28 июля 2007 г., Калмыкия)

скорости ветра равняются: U_G = 3,61 м/с — направление «юг-север»; V G = - 1,75 м/с — направление «запад-восток», соответственно, скорость геострофического ветра — 12

G = (UG + VG ) = 4,02 м/с.   Геострофическая скорость отклонена от направления оси роллов на угол £набл « 25° .

Для широты точки наблюдения 0 = 45,31° имеем параметр Кориолиса f = Osin 0 = 5,184 -10 ^{- 5} , число Рейнольдса Re = g/ ( Kf ) 1/2 ~ 76 <  100 • Подобные значения качественно отвечают условиям развития валиковой циркуляции в атмосферном пограничном слое при наличии конвекции [53].

5.    Заключение

Рассмотрен нелинейный режим формирования вторичных вихревых структур в АПС с использованием двухмасштабной модели атмосферного пограничного слоя, мезомасштабной атмосферной модели RAMS, данных наблюдений за структурами в Калмыкии. Числа Рейнольдса меняются в диапазоне 100 ^400. При значениях числа Рейнольдса Re « 150 происходит переход от одного типа неустойчивости к другому, вследствие чего резко меняются знак и величина угла ориентации валиков: от £«-15° до е« 10°^15° . С ростом числа Re увеличиваются средняя энергия и спиральность. В диапазоне Re = 200 ^300 зависимость близка к линейной. Исследованы пространственные распределения компонент скоростей, завихренности, спиральности. Параметры, характеризующие квазипараллельные валиковые структуры, вычислены до момента установления стационарного режима при различных значениях Re и углов ориентации валов. Отмечено развитие асимметрии продольной компоненты скорости, положительных и отрицательных значений спиральности валиковых структур (по и против направления геострофического ветра) с ростом Re вслед за увеличением экстремальных значений амплитуды отрицательной продольной компоненты скорости (против направления геострофического ветра) по сравнению с положительной амплитудой (по направлению ветра). Амплитуды положительной составляющей спиральности также превышают амплитуды отрицательной составляющей спиральности. Наблюдаемая динамика асимметрии имеет черты, по всей видимости, свойственные и хорошо известному как в лабораторных, так и геофизических системах явлению циклон-антициклонной асимметрии, при котором в системах с вращением более интенсивными и долгоживущими оказываются образования с антициклоническим вращением. Качественное сравнение асимметрии структур, установленной путем двухмасштабного моделирования и измерениями когерентных структур методами акустического зондирования в АПС (Калмыкия, июль 2007 года), показало похожее распределение. Получено неплохое соответствие результатов численного моделирования нелинейного развития структур в экмановском слое в рамках мезомасштабной атмосферной модели RAMS присутствующим в пограничном слое пространственным распределениям циркуляционных движений. Значения эффективного числа Рейнольдса и профиль коэффициента турбулентной вязкости, полученный в представлении вихревой вязкости, характерны для условий неустойчивой стратификации.

Авторы признательны Г.С. Голицыну, М.А. Каллистратовой, В.Ф. Крамару за внимание к работе и конструктивные замечания.

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 14-27-00134) и РФФИ (проекты № 14-05-00847-а и № 17-05-01116-а).