Нелинейное вязкоупругое поведение волокон миокарда: гистерезис кривых «сила-длина» и релаксация деформации

До настоящего времени при анализе зависимостей «пассивное напряжение– деформация» для мышцы, как правило, используются одномерные модели реологического состояния, другими словами, не учитываются поперечные деформации [1, 2]. В то же время, экспериментально установлена нелинейная зависимость поперечного размера деформируемого препарата от продольного растяжения [3, 4]. Впервые учет существенного вклада поперечных деформаций в происхождение нелинейной зависимости «сила–длина» для изолированных препаратов миокарда был проведен в работах [4–6], где исследованы двумерные топологические структуры, при деформации которых определяющую роль играет геометрический эффект «схлапывания». Возможность адекватного описания статической зависимости «пассивное напряжение–деформация» для папиллярных мышц была исследована с использованием классических форм в виде линейных упругих элементов,

организованных в структуру, подобную морфологически-функциональной единице миокардиальной ткани [4].

В рамках предложенной модели показано, что имеет достаточное основание предположение о функционировании морфологических структур миокардиальной ткани с различной линейной жесткостью в разных участках физиологического диапазона деформаций без введения дополнительных предположений об общем характере нелинейности во всем диапазоне деформаций. Так, в диапазоне начальных длин препарата при деформации сначала включаются более мягкие элементы, оказывающие наименьшее сопротивление генерации мышцей активного напряжения. С ростом деформации подключаются более жесткие элементы, препятствующие разрушению ткани. Отметим, что введение геометрического фактора ранее было успешно использовано при математическом моделировании зависимости активного напряжения от длины мышцы [3].

Одной из физиологических функций вязкости в живых тканях является предохранение их от разрывов при резких деформациях. Вязкостью обладают практически все биологические ткани, однако ее природа в мышечной ткани не ясна до сих пор. Установлено, что ответ на достаточно быструю деформацию сопровождается релаксацией мышечного напряжения в изолированном невозбужденном состоянии. В ряде экспериментов [1, 2, 8] показано, что процессы релаксации напряжения зависят не только от величины скачка деформации, но и от исходной (начальной) длины препарата. Такая зависимость не воспроизводится ни в одной из реологических моделей без введения дополнительного искусственного предположения о зависимости коэффициента вязкости от длины препарата [9].

Вязкие свойства проявляются на всех уровнях организации мышечной ткани – от клеточного до органного. Причинами вязкого поведения могут являться, по-видимому, фильтрация тканевой жидкости через поры, трение скольжения сократительных элементов и других внутриклеточных структур при их движении в цитоплазме при деформации и, наконец, собственное вязкоупругое поведение молекул белков цитоскелета, в частности, титина [9].

При динамических нагружениях геометрическая структура сказывается не только на упругих, но и на вязких свойствах миокарда. Следовательно, при нагрузке, зависящей от времени и от начальных условий, наряду с упругой нелинейностью, могут проявляться и нелинейные вязкие свойства миокарда.

Цель исследования

Исследование ставит целью описать упругие и вязкие свойства пассивного миокарда при периодической и ступенчатой нагрузке в области физиологических деформаций ( ε ~ 0,3 ) на основе предложенных в [4] простых двумерных структур, отражающих функциональные особенности морфологической единицы миокарда, составленных из линейных гуковских элементов с включенными параллельно им вязкими элементами (ньютоновскими демпферами). На основе сравнения с экспериментально полученными кривыми гистерезиса «сила–длина» оценить адекватность той или иной модели без введения зависимости коэффициентов упругости и вязкости от длины и определить значения вязких постоянных составляющих элементов. Исследовать особенности релаксации деформации при заданном периодическом или ступенчатом изменении нагрузки в зависимости от величины параметров вязкости первичных элементов.

Рис. 1. Схематическое изображение препарата миокарда, зафиксированного лигатурами на штоках

Методика физиологического эксперимента

Приготовление препаратов

Эксперименты выполнены на папиллярных мышцах правого желудочка крыс, кроликов, кошек и морских свинок. Перед вскрытием животного проводилась инъекция гепарина для уменьшения свертываемости крови. Доза гепарина для кроликов составляла в среднем 0,5 мл/кг, для крыс – 0,2 мл/кг. Спустя 5–15 минут после инъекции гепарина проводилась эвтаназия в соответствии с международными правилами [10].

Использовали раствор Кребса-Рингера, содержащий (в миллилитрах): 98 NaCl, 4,7 KCl, 2,4 MgSO 4 *7H 2 O, 25 NaHCO 3 , 1,25 CaCl 2 *2H 2 O, глюкоза 4,5, при температуре 30⁰С, барбатируемый 100%-м кислородом. После приготовления раствора измеряли величину pH при температуре раствора 30⁰С. Буферные компоненты раствора ( TRIZMA , Sigma-Aldrich ) обеспечивали уровень pH в интервале от 7,30 до 7,35.

После усыпления животного производили разрез по средней грудинной линии, затем сердце быстро извлекали и помещали в препаровальную термостатируемую кювету объемом 50 мл с физиологическим раствором. Препарирование вели под бинокулярным микроскопом МБС-10. Правый желудочек сердца вскрывали по нисходящей коронарной артерии вдоль межжелудочковой перегородки, иссекали папиллярную мышцу и помещали в ванночку экспериментальной установки. При этом отбирали преимущественно тонкие и длинные препараты. Концы препарата фиксировали на штоках датчика силы и мотора длины наложением ниточных лигатур на оба конца препарата (рис. 1).

На начальном этапе подготовки к эксперименту осуществляли отбор и оценку сократительных свойств препаратов. Если сразу после закрепления препарата развиваемая им активная сила не превышала 50 мг, то препарат считался поврежденным и дальнейшие эксперименты над ним не проводились. Если же развиваемая препаратом сила составляла около 100 мг для крыс, а для препаратов кролика около 400 мг, то после наложения дополнительных лигатур препарат изометрически сокращался в течение 30–60 минут (период «врабатывания» препарата). В течение этого периода времени при непрерывном питании физиологическим раствором при температуре 300С, перфузии кислородом и включенной стимуляции активная сила, развиваемая препаратом, возрастала в 2–3 раза, а пассивное напряжение падало. По истечении периода врабатывания препарата, при условии восстановления его сократительных свойств, реализовывали экспериментальный протокол.

Протокол эксперимента

В качестве тестирующих механических воздействий использовали периодические деформации синусоидальной, прямоугольной, треугольной, “пилообразной” формы с изменяющейся частотой. С помощью такого типа воздействий нами измерены динамические реологические характеристики папиллярных мышц (компоненты динамического модуля упругости и диссипативные потери энергии при деформации). Деформация задавалась в пределах 10% от рабочей длины с целью выявить наличие нелинейности. Пилообразное изменение длины папиллярной мышцы задавали с амплитудой от 0,05 до 0,3 l_w со скоростью от 0,001 до 0,1 длины мышцы в секунду.

Препарат разделяли на ряд сегментов с помощью шипов кактуса. Изменения длины сегментов регистрировали с помощью компьютерной системы технического зрения [11]. Для выявления продольного перемещения метки по оси препарата использовали среднее значение положений метки с одного и другого края препарата. Этот прием позволил оценить характер чисто продольного перемещения. Несмотря на изометрический режим, справедливый для препарата в целом, наблюдали изменения длины сегмента в продольном направлении, которые были наиболее выражены в фазе расслабления и достигали нескольких процентов от длины сегмента.

Образцы препаратов

AR013: морская свинка, l_o = 3,88 мм, l_w = 4,82 мм, диаметр h = 0,42 мм, четыре метки, амплитуда продольного растяжения в форме пилы = 940 мкм, период T = 1000 с и

AZ038: кот, l_o = 3,65 мм, l_w = 4,54 мм, диаметр h = 0,9 мм, две метки, амплитуда продольного растяжения в форме пилы =890 мкм, период T = 333 с.

Результаты эксперимента

При линейном растяжении препарата пассивное напряжение возрастало приблизительно по экспоненциальному закону. Характер изменения длины центральных сегментов при этом был самый разнообразный – от линейного удлинения, через немонотонный, до укорочения сегмента при растяжении всего препарата. Последнее наблюдение при нанесении меток тушью зарегистрировано и в работе [12].

При “пилообразной” деформации препарата в координатах “напряжение– деформация” нами зарегистрирована характерная петля гистерезиса [1]. При этом показано, что движение по петле гистерезиса в исследованной вязкоупругой структуре пассивного миокарда всегда направлено по часовой стрелке, что характерно для диссипативных систем. Вид петли гистерезиса свидетельствует о нелинейности реологических характеристик препарата миокарда. В данном случае под “линейностью” понимается пропорциональность амплитуд напряжений и деформаций. Нелинейность петли гистерезиса проявляется при деформациях, превышающих 1–2 % от текущей длины препарата.

Обнаружено, что нелинейность связи “деформация–напряжение” при динамических испытаниях проявляется тем больше, чем больше рабочая длина папиллярной мышцы, т.е. длина, на которую растянули препарат перед испытаниями.

Такое поведение характерно как для всего препарата, так и для его центрального сегмента.

Значения комплексного модуля упругости и энергии диссипации препарата и его центрального сегмента зависят от скорости деформации. При увеличении скорости деформации препарата на порядок единиц длин мышцы в секунду величина модуля возрастает на десять процентов. Характер зависимости в целом препарате не отличается от вида зависимости для сегмента. Однако принципиально важным является то обстоятельство, что абсолютные значения комплексного модуля упругости при всех исследованных скоростях деформации для целого препарата выше, чем для сегмента. В группе “мягких” препаратов ( P pas / P act <  0,5) тангенциальный модуль Юнга по начальной части гистерезиса в целом препарате составляет 15 ± 2 кН/м², а в группе жестких препаратов - на порядок больше. Наличие более податливого центрального участка папиллярной мышцы в эксперименте проявляется в том, что при любой деформации растяжения на концах препарата его центральный сегмент деформируется сильнее. Модуль упругости составляет для центральных сегментов “мягких” препаратов 11 ± 2 кН/м². Таким образом, модуль упругости как целого препарата, так и его сегмента возрастает с увеличением скорости деформации и с увеличением исходной длины.

Величины значений тангенциального модуля упругости, полученные в наших экспериментах, совпадают со значениями модуля пассивного напряжения миокарда, полученными другими авторами: 14 кН/м2 - для папиллярной мышцы кошки [13], 15,7 кН/м2 - для папиллярной мышцы крысы [14]. Различная величина деформации и значений модуля упругости целого препарата и его сегмента свидетельствует о выраженной продольной неоднородности реологических характеристик миокарда.

Кроме того, показано, что при задании ступенчатой деформации вязкоупругое поведение сердечной мышцы проявляется в релаксации напряжения на концах препарата, которое не сопровождается изменением длины центрального сегмента. В сопоставлении с данными об изменении поперечных размеров, полученными в других экспериментах, можно предположить, что релаксация сопровождается изменениями размеров в различных сечениях образца.

Выбор и описание моделей

При моделировании вязкоупругих динамических свойств сердечной мышцы (без учета ее массы, что справедливо при достаточно низкой частоте периодической нагрузки) мы будем опираться на предложенные в работе [4] двумерные структуры, составленные из гуковских линейных упругих элементов, соединенных шарнирами без трения в точках типа а и b (рис. 2a). Вязкость учитывается введением ньютоновских демпферов, включенных параллельно упругим элементам. При этом часть из моделей, исследованных в [2], мы опустим, учитывая их неадекватные статические характеристики. Таким образом, в данной работе мы остановимся на моделях ромбической и параллельной геометрии 2-6 и 9 в обозначениях работы [4].

Рассмотрены два варианта постановки задачи исследования динамики. В первом из них считается заданной зависимость от времени деформации какого-либо первичного элемента модели в виде периодической функции синусоидальной или пилообразной формы. При этом предполагается, что этот элемент обладает вязкостью. Например, при деформации поперечного элемента 8 ₃ ( t ) вязкая сила пропорциональна П ₃ d8 ₃ / dt , где п ₃ - коэффициент вязкости. Зависимости от времени деформации всех

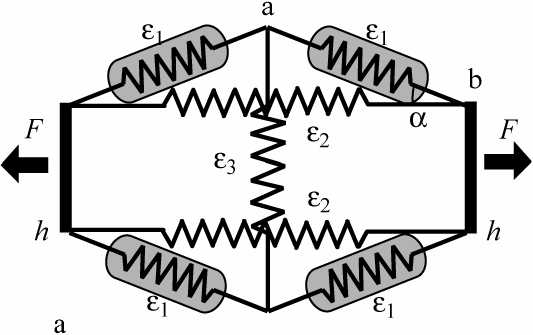
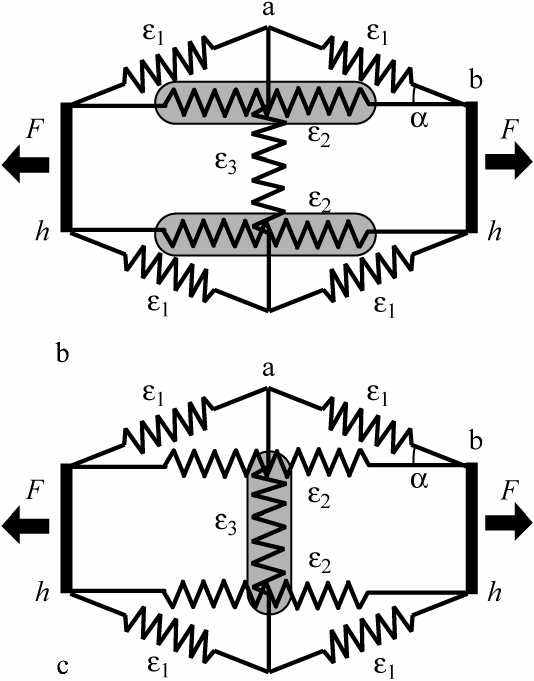
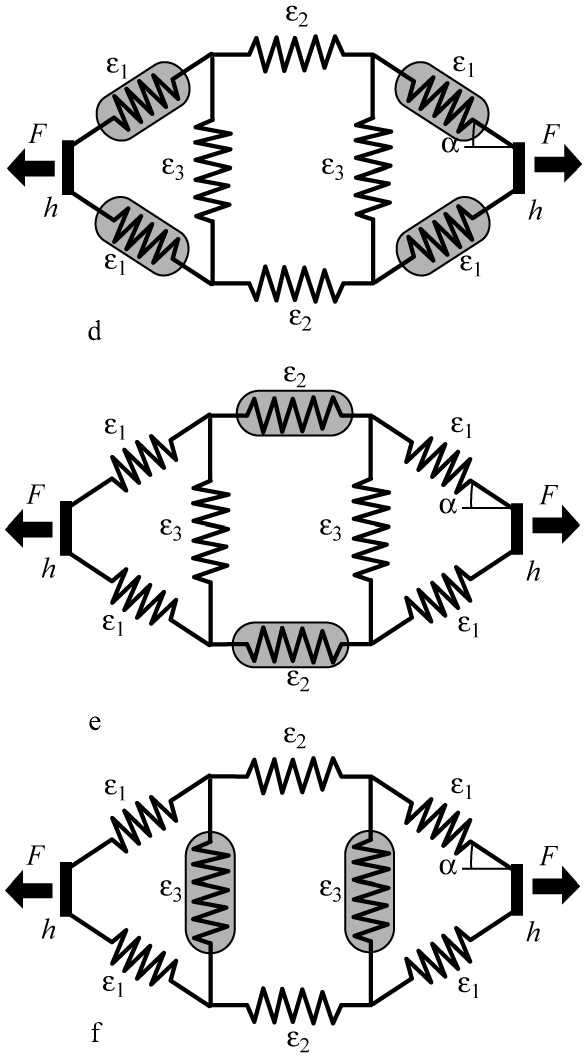
Рис. 2. Схемы моделей RLH1 (a), RLH2 (b), RLH3 (c) ромбической (слева) и параллельной PH1 (d), PH2 (e), PH3 (f) (справа) геометрии. Первичные элементы, обладающие вязкостью, заштрихованы серым цветом. Кроме представленных, рассмотрены ромбические модели без продольного элемента (RH1, RH2, RH3), а также варианты всех моделей при h =0 (RL1, RL2, RL3, P1, P2, P3, R1, R2, R3)

других элементов, общая продольная деформация модели, а также результирующая сила F(t) находятся в результате решения системы нелинейных уравнений с учетом вязкой силы, пропорциональной скорости деформации. В такой постановке удается получить решение задачи, задавая деформацию того элемента, который обладает вязкостью. Таким образом, рассмотрены варианты ромбической и параллельной геометрии, в которых последовательно учитывается вязкость наклонного η ₁ dε ₁ I dt , продольного η ₂ dε ₂ Idt и поперечного η ₃ dε ₃ Idt элементов (см. рис. 2).

Во втором варианте постановки задачи считается заданной зависимость от времени внешней нагрузки F ( t ) в виде периодической или ступенчатой функции. Скорости деформации первичных элементов dε ₁ I dt , dε ₂ I dt и dε ₃ Idt , а также сами деформации ε ₁ , ε ₂ и ε ₃ определяются при решении системы нелинейных дифференциальных уравнений первого порядка с нулевыми начальными условиями. Полученные решения описывают релаксацию деформации различных элементов и структуры в целом в форме переходных процессов с выходом на квазистационарный предел.

В данной работе мы не рассматриваем вопросы, связанные с решением обратной задачи, т.е. с релаксацией напряжения в сердечной мышце при ступенчатой деформации. Это требует использования моделей, в которых упругий и вязкий первичные элементы соединены последовательно (аналогичных модели Максвелла), что выходит за рамки настоящей работы и составит предмет отдельной публикации.

Уравнения для ромбической модели и модели параллелограмма

Приведем основные уравнения, описывающие реологические характеристики миокарда при учете вязких свойств в отдельных упругих элементах модели. Решения, описывающие кривые гистерезиса силы, получены при задаваемой деформации для моделей, наиболее адекватно описывающих статические упругие свойства [4]. Используем обозначения:

• a - угол наклонного элемента;

• h – поперечник муфты закрепления (заштриховано на рис. 2);

• F – сила нагрузки на муфту;

• l , l ₀ – продольная длина, начальная продольная длина;

• l ₁ , l ₂ , l ₃ – длины наклонного, продольного и поперечного элементов;

• l ₁₀, l ₂₀ , l ₃₀ – соответствующие начальные длины;

• ε ₁ , ε ₂ , ε ₃ – однородные относительные деформации;

• £ 1 = d£ 1 (dt , £ 2 = d£ 2 jdt , £ ₃ = d£ 3 / dt - скорости деформаций;

• K ₁ , K ₂ , K ₃ – коэффициенты жесткости элементов;

• η ₁ , η ₂ , η ₃ – коэффициенты вязкости.

Вязкость наклонного элемента

Считая деформацию наклонного элемента £ 1 = £ 1 ( t ) и ее производную

£1 = d£1 jdi; заданными функциями времени, в модели ромба (рис. 2a) без продольного элемента RH1 из условия равенства упругих и вязких сил в точках a и b получим:

2sin a — + — £

I K i к 2 ¹ J

+— = 0, κ ₃

£ 3 =-

Г

1 -Т

V   ² 3 А

1 +    У /^{2 к} 3 ² 3

I                                                —

Л-1

^£ 1 / ^К 1 ⁺ П 1 ^£1 / ^к 2 J

.

Выражение (3) позволяет получить полную деформацию:

£ = -1 + Vy12 -(y3 - y)2

и в соответствии со вторым уравнением (1) и соотношением cos a = (1 + £ )/ y 1 решение задачи определения силы f ( t ) при заданной деформации.

При решении этой задачи для модели ромба с продольными элементами RLH1 с учетом s = £ 2 справедливо второе уравнение (1), в левую часть которого добавляется слагаемое ε ₂ . Отметим, что для модели параллелограмма выполняется формула (4) с добавлением слагаемого у₂ в правую часть и при учете соотношения f ( t ) = 2 s ₂( t ).

Вязкость продольного элемента

Для модели с вязким продольным элементом RLH2 соответствующая система уравнений имеет вид:

εε

2sin a — + — = 0,

κκ

1     3(5)

εη

2cos a — + £2 + — £2 = j. κ1

Учитывая (2), из первого уравнения (5) найдем соотношение, обратное (3) и выражающее деформацию наклонного элемента через деформацию поперечного:

£,=-fi + ^^(6)

I      ^K ' X 1 ^£ 3 )

Зависимость от времени продольной деформации £ ₂ и ее производной £ 2

считается заданной. При этом зависимость ε ₃ ( ε ₂ ) находится из решения уравнения

(£2 +1)2 = У'2 -(У3 - Y )2,(7)

с учетом (6) и далее из (6) находим зависимость ε ₁( ε ₂) . Зависимость силы от времени f ( t ) находим далее из второго уравнения (5).

Для модели параллелограмма PH2 в системе уравнений (5) исключается слагаемое ε2 , и дополнительно появляется уравнение

f = 2 £ 2

I

⁺ 72 ^£ 2 , k 2    7

и аналогично (4) для полной деформации

^£ = y 2 ^{- 1 +} V y 12 ' ⁽ y 3 ' ^{Y ) 2} .

Вязкость поперечного элемента

Считаем заданной функцией времени деформацию поперечного элемента ε ₃ и соответствующую скорость деформации £ ₃. Система уравнений для модели ромба

RLH3 в этом случае	2 sin a — + -^ 3 + — s 3 = 0, К '    К 3    k 2                                        (11) sl 2cos a--+ s 2 = j К 1
позволяет получить элемента	соотношение, аналогичное (6), для деформации наклонного

£1 = —

(

¹ +

V

У 3 - Y

л-1

^КЛ ^£ 3 / ^К 3 ⁺ П 3 k 2 2 ^£ 3 L

.

При этом справедлива формула (4) для продольной деформации £ = £ ₂, которая совместно со вторым уравнением (11) позволяет получить решение задачи определения f ( t ).

Решение задачи для параллелограмма PH3 дает аналогичную (11) систему уравнений без слагаемого в ₂ и c дополнительным условием f = 2 в ₂.

Уравнения релаксации деформации при заданной нагрузке

Другой подход к исследованию вязкоупругой динамики в рамках предложенных двумерных моделей состоит в решении системы дифференциальных уравнений для деформаций элементов при заданной зависимости от времени нагрузки f ( t ) . Приведем систему уравнений для модели ромба без продольного элемента R13 при h= 0.

2sin а — + — £

V К k 2 ¹

л

)

εη

+ — +— в = 0, κ 3    k 2 ³

2cos а ^ + П £

V К k 2 ¹ )

Преобразуем систему (13) к виду,

= f ( t ).

удобному для применения стандартных

методов решения систем нелинейных дифференциальных уравнений:

где Т 1 =

1 —

² y ^— r V ^y 1 )

- 1

и

П _£ = k ₂ ¹

П £ k ₂

—

• 3 =

- £ 1 + 2 Ч^, £ 3 ) f ( t ),

κ ₁

-

Т _; =— 2

- в 3 + 2 ^ 3 ( £„ £ 3 ) f ( t ),

κ ₃

1 —

y ₁

- 1

.

V У з — Y )

Для модели ромба с продольным элементом RL123 при h =0 получим систему трех нелинейных дифференциальных уравнений

( 1              ^

— ^£ 1 ⁺ -^ ^ ^ 1 ^ 1 ^{1 + £} 2 ⁺ ^2 ^ ^ 2 = ^{f (} t ), k

V ^К 1     ^k 2 J

—£ 3 + ^П 3 £ 3 + 2 ^— £ 1 + у ¹ i i 1 ^3

V ^K 1      ^k 2    ) У 1

κ ₃

η ₃

k ₂

3^ = 0,

^£ 2 ^{( 1 + £} 2 ) = ^£ 1 ^ 1 У 1 ^{— £} 3 ^ 3 У 3 .

Последнее уравнение (15) получено дифференцированием соотношения (7) при

Y = 0.

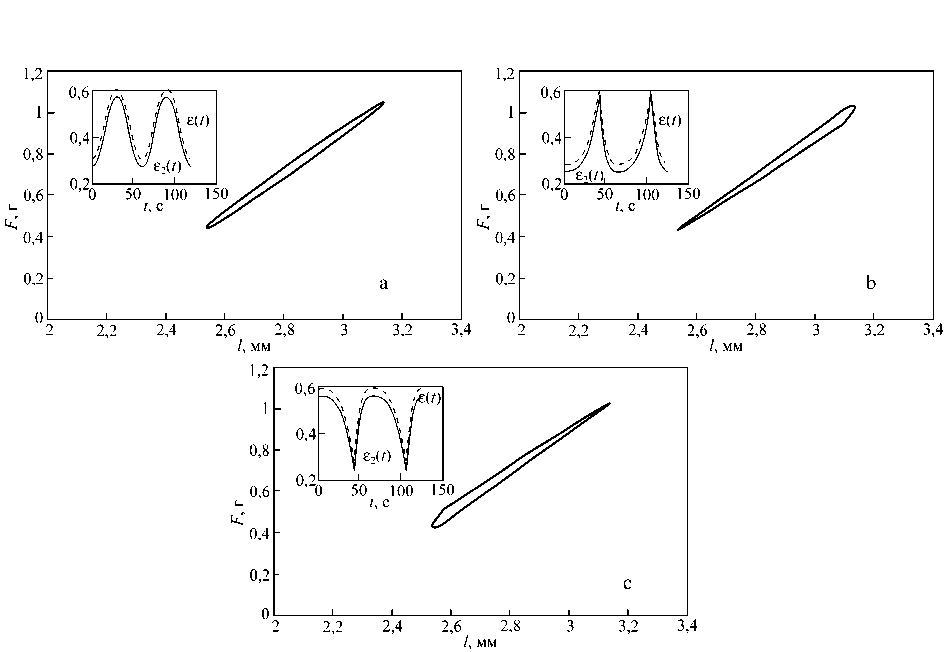
Рис. 3. Кривые гистерезиса, полученные в модели ромба с вязким продольным элементом RLH2 в области линейной статической кривой сила-длина при синусоидальной (a) и кубической пилообразной (b и c) нагрузке. Начальная продольная деформация 0,3, максимальная 0,6. На вставках приведены зависимости от времени для задаваемой и полной деформации. Значения параметров: l_o =2 мм, l_{o 1}=1,07 мм, l_{o 3}=1,25 мм, K ₁=1,0 г/мм, K ₂= K ₃=0,01 г/мм, H ₂=0,8 с∙г/м (a), H ₂=0,5 с∙г/мм (b, c)

Результаты моделирования1.    Гистерезис

Влияние вида задаваемой деформации

Для формы задаваемой деформации мы использовали синусоидальную и пилообразную функцию времени (кусочно-линейного, квадратичного и кубического вида) с расположением зубцов вверх и вниз. На рис. 3a представлена кривая гистерезиса для модели ромба при синусоидальной зависимости от времени задаваемой деформации продольного элемента в области начального линейного участка стационарной кривой «сила–деформация». Кривая напряжения имеет симметричную форму в соответствии с тем, что производная деформации, определяющая вязкие свойства, является непрерывной и плавной функцией. В координатах «напряжение– деформация» в этом случае получена линейная симметричная гистерезисная зависимость эллипсовидной формы. Кривые гистерезиса в случаях с входным сигналом пилообразной функции времени квадратичного и кубического вида имеют разрывы в верхней и нижней частях, соответственно расположению зубцов (рис. 3 b и c). Такого же рода особенности кривых гистерезиса вблизи точек скачков производной деформации характерны для других исследованных моделей.

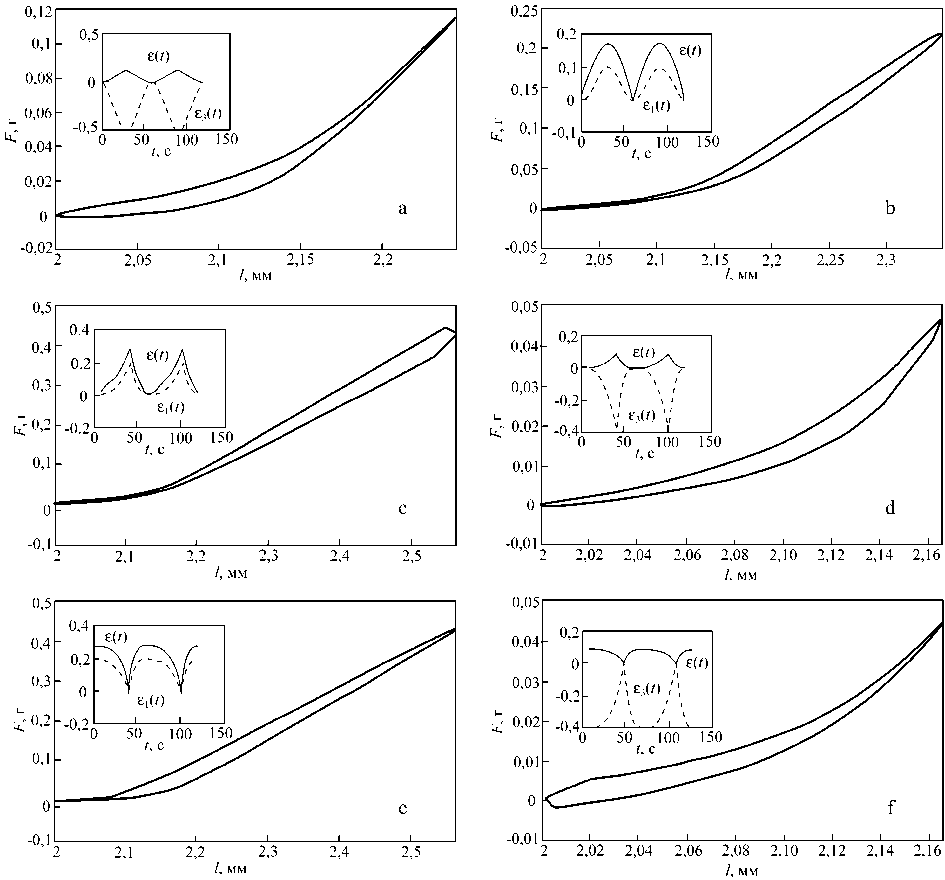
Рис. 4. Кривые гистерезиса, полученные в моделях ромба с вязким мягким элементом RLH3 при синусоидальной (a) и кубической пилообразной (d, f) нагрузках и в моделях ромба с вязким жестким элементом RLH1, соответственно (b, c и e). Геометрические параметры и параметры жесткости элементов указаны в подписи к рис. 3, H 3 =0.05 (a), H 3 =0.02 (d и f), H 1 =0.5 (b), H 1 =0.3 с∙г/мм (c и e)

Влияние вязкости различных первичных элементов

Кривые гистерезиса, полученные для моделей с поперечным или наклонным вязким элементом, во всем диапазоне деформаций, включающем нелинейную область, имеют асимметрию либо при малых, либо при больших деформациях. Показано, что этот эффект определяется тем, что мягкий поперечный элемент работает в основном при малых деформациях и кривая гистерезиса имеет расширение при малых деформациях (рис. 4a). В моделях с вязким наклонным элементом при достижении больших величин деформаций, когда начинает работать жесткий элемент, кривая гистерезиса имеет расширение при больших деформациях (рис. 4b). Аналогичный эффект наблюдается и для пилообразной зависимости от времени задаваемой деформации (рис. 4 c–f)).

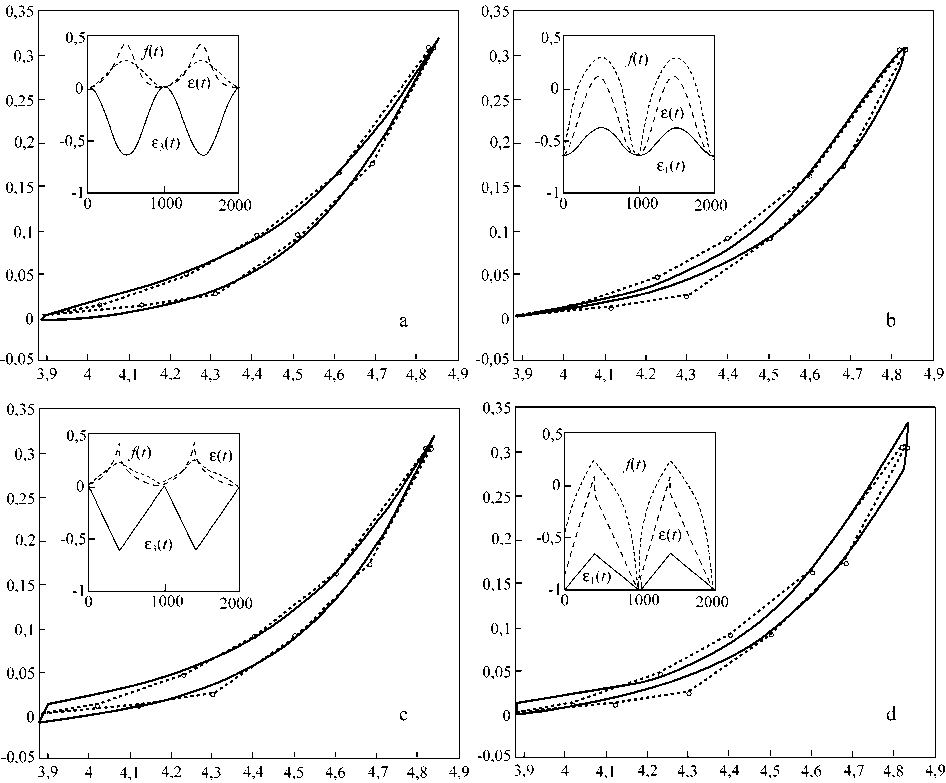
Рис. 5. Сопоставление кривых гистерезиса, полученных в различных моделях, с данными эксперимента AR013. Значения геометрических параметров и параметров упругости одинаковы во всех вариантах: l o 1 =2,276 мм, l o 2 =3,88 мм, l o 3 =2,8 мм, h =0,42 мм, K 1 =0,9 г/мм, K 2 = K 3 =0,02 г/мм. Синусоидальная нагрузка: (a) модель с вязким поперечным элементом RLH3, H ₃=1,5 с∙г/мм, максимальная поперечная деформация 8 _3max =- 0,64, максимальная полная деформация

8 m ax = 0,249; (b) модель с вязким наклонным элементом RLH1 при H 1 =16 ст/мм, 8 _1max = 0,07,

8 _max = 0,246. Пилообразная нагрузка: (c) H ₃=2  ст/мм,    8 _3max =- 0,61,    8 _max = 0,246,

(d) H 1 =20 ст/мм, 8 imax = 0,07, 8 max = 0,246

Сравнение с экспериментом

В натуральных экспериментах задавалось смещение закрепляющих концов препарата в виде пилообразной функции времени в связи с тем, что при линейном нарастании и спаде нагрузки упрощается анализ ответной реакции нелинейного объекта. Введение меток позволило исследовать продольную неоднородность реологических характеристик. Однако оказалось практически невозможно выделить структуры, локально ответственные за те или иные реологические характеристики препарата в целом. Однородность деформации по всей длине препарата не была подтверждена.

В численных экспериментах задавалась пилообразная и синусоидальная форма однородной деформации какого-либо из составляющих элементов модели. При этом форма полной результирующей продольной деформации была существенно различной и могла в той или иной мере моделировать реально задаваемую линейную форму нагрузки. Кроме того, в численных экспериментах в предположении, что продольные линейные смещения концов образца могут трансформироваться в неоднородные продольные локальные деформации, рассмотрены нелинейные синусоидальные, квадратичные и кубические по форме задаваемые деформации. Неоднородность продольной деформации может быть исследована в моделях параллелограмма PLH (рис. 2 d, e, f), в которых деформации продольного элемента отличаются от деформации структур вблизи муфты закрепления.

Для сравнения экспериментальных данных с результатами моделирования использованы два эксперимента AR013 и AZ038, проведенные на папиллярных мышцах с различными геометрическими размерами и начальной жесткостью. В качестве первого шага мы ограничились ромбическими моделями (рис. 2 a, c).

Кривая гистерезиса, полученная в ромбической модели с продольным элементом и муфтой RLH3, при учете вязкости мягкого поперечного элемента для синусоидальной задаваемой деформации, достаточно хорошо в целом описывает эксперимент AR013 (рис. 5a), хотя имеются отклонения как при малых, так и при максимальных деформациях. Теоретическая кривая в модели с вязким жестким наклонным элементом RLH1 (рис. 5b) хорошо описывает максимальные деформации, но не работает при малых деформациях. На рис. 5 c и d представлены соответствующие экспериментальные и модельные кривые гистерезиса для задаваемой деформации кусочно-линейной формы.

Следует обратить внимание, что значения параметров жесткости и вязкости, полученные в результате подгонки, несколько изменяются при изменении формы зависимости от времени задаваемой деформации элемента. Для более детального сравнения нужны численные эксперименты при разной крутизне (скорости изменения) пилообразной нагрузки и при различных начальных длинах препарата при одной и той же скорости изменения деформации в условиях нелинейности стационарной кривой «сила–длина».

Для эксперимента AZ038 характерна нерегулярная форма опытной кривой гистерезиса. В этом случае результаты моделирования при задаваемой деформации синусоидального вида (рис. 6 a, b) по средним квадратичным отклонениям хуже, чем при использовании пилообразной формы кривой (рис. 6 c, d). Однако, и в этом случае согласие экспериментальных данных с теоретическими кривыми наблюдается либо при малых, либо при максимальных деформациях.

Для оценки величины упругих и вязких параметров, аналогично тому, как это сделано в работе [2], предположим, что отношение поперечника первичного элемента к его длине равно 0,2. При этом для поперечного элемента с длиной 2,8 мм и коэффициентом упругости K ₃ = 0,02 г/мм получим значение модуля Юнга E ₃ = 0,23 г/мм²=2,2 кН/м². Аналогично для наклонного элемента с длиной 2,28 mm и коэффициентом упругости K ₁ = 0,9 г/мм получим E ₁ = 12,6 г/мм²=123 кН/м². Предполагая, что площадь боковой поверхности элемента представляет рабочую поверхность возникновения ньютоновской вязкости, при значении параметра вязкости H ₁ = 16 с∙г/мм, получим для коэффициента вязкости η ₁ = 11 с∙кН/м² и, соответственно, для H ₃ = 1,5 с∙г/мм η ₃ = 0,8 с∙кН/м². Для сравнения приведем значения модуля Юнга эластина 600 кН/м² и коэффициента вязкости вазелина 0,5 с∙кН/м².

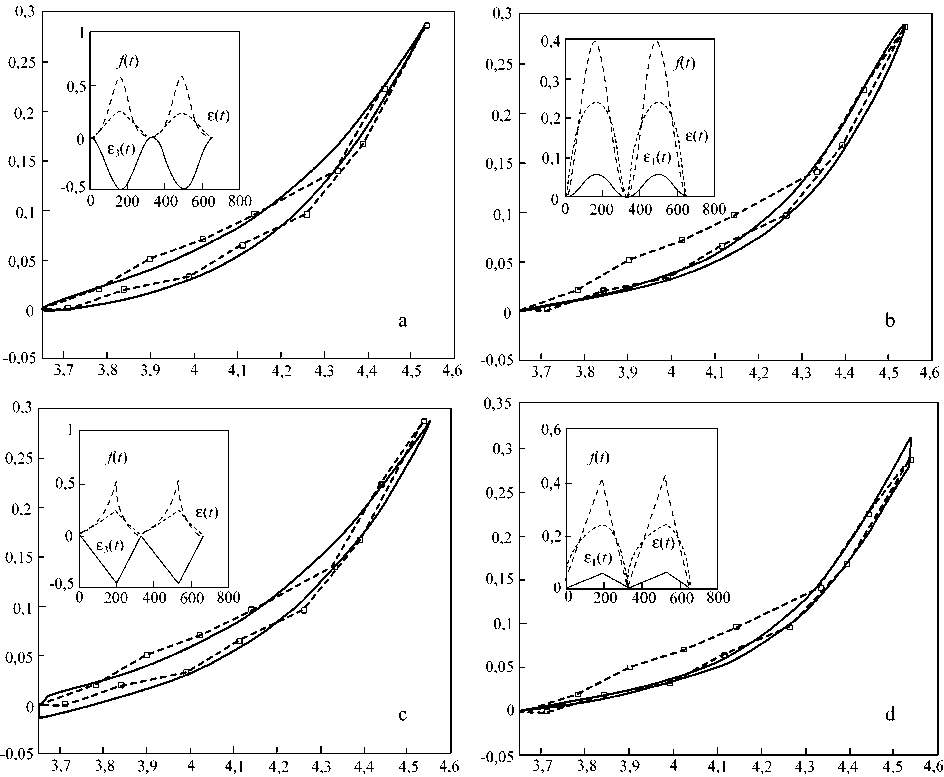
Рис. 6. Сопоставление кривых гистерезиса, полученных в различных моделях, с данными эксперимента AZ038. Значения геометрических параметров и параметров упругости одинаковы во всех вариантах: l_{o 1}=2,157 мм, l_{o 2}=3,65 мм, l_{o 3}=3,2 мм, h =0,9 мм. Синусоидальная нагрузка: (a) модель с вязким поперечным элементом RLH3 при K ₁=0,95 г/мм, K ₂= K ₃=0,027 г/мм, H ₃=0,5 с∙г/мм, £ _{3 m ax} = - 0,5, £ _max = 0,243 ; (b) модель с вязким наклонным элементом RLH1 при , К 1 =1,05 г/мм, К ₂= К 3 =0,02 г/мм, H 1 =5 ст/мм, £ _1max = 0,06, £ _max = 0,243 . Пилообразная нагрузка RLH3: (c) К =0,85 г/мм, К ₂= К =0,03 г/мм, Н ₃=0,8 ст/мм, £    =- 0,455, £   = 0,237, (d) H =5 ст/мм,

3max              max

£ 1max = 0,06, £ max = 0,243

• 2.    Релаксации деформации

На рис. 7 a и b представлены кривые релаксации деформации наклонного, продольного и поперечного элементов в ромбической модели при заданной внешней силовой возрастающей и убывающей ступенчатой нагрузке. Нетрудно заметить, что времена релаксации первичных упругих элементов пропорциональны соответствующим коэффициентам вязкости, и в течение периода действия нагрузки релаксация менее вязких элементов практически завершается, тогда как более вязких продолжается. Это отчетливо видно при синусоидальной и пилообразной внешней нагрузке (рис. 7 c, d).

Сравнение с экспериментом в этом случае не было проведено, поскольку имеющиеся опытные данные относятся к релаксации напряжения при ступенчатоизменяемой продольной деформации образца. Помимо рассмотрения вопроса об

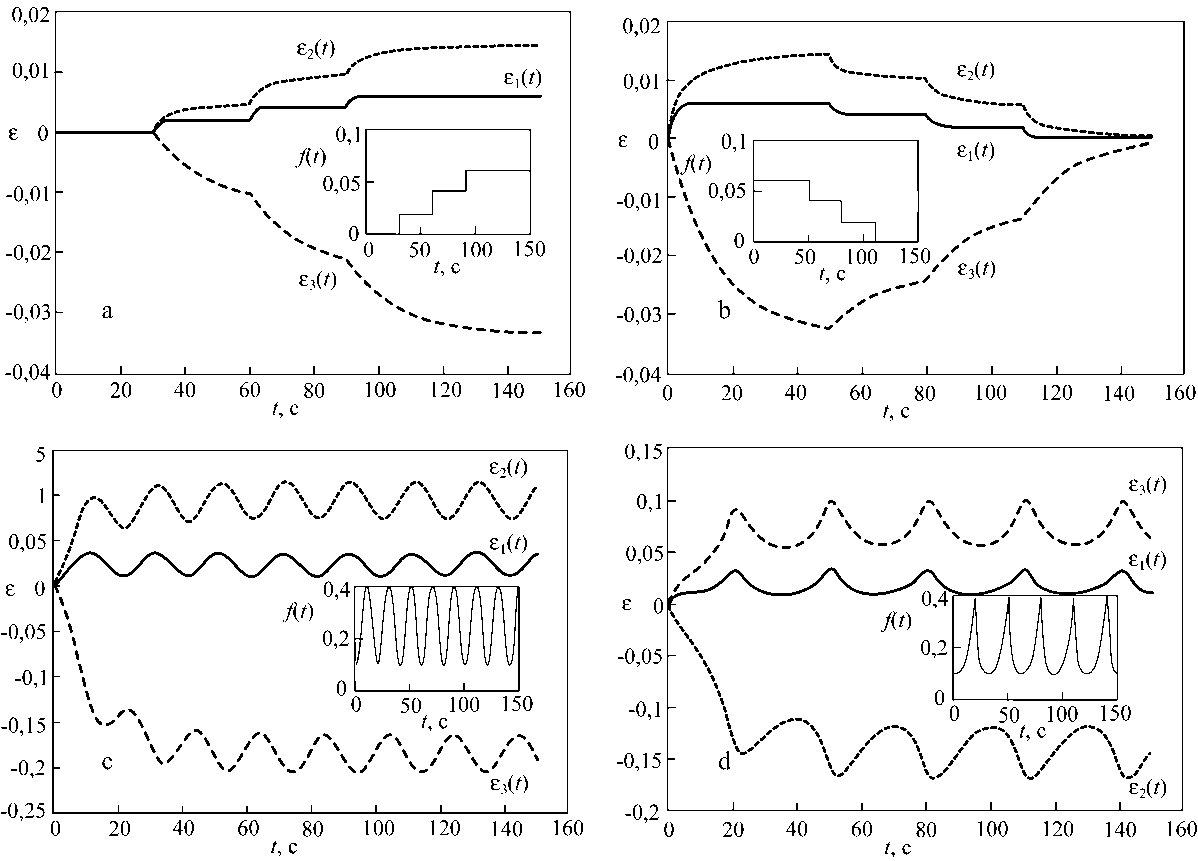
Рис. 7. Кривые релаксации деформации различных элементов модели RLH13. Геометрические параметры и параметры жесткости элементов указаны в подписи к рис. 3, H ₁=1,0 с∙г/мм; H ₃=0,01 с∙г/мм. Ступенчатая восходящая (a), нисходящая (b), синусоидальная (c) и пилообразная (d) зависимости от времени задаваемой нагрузки f ( t ) (на вставках)

ударной жесткости, который возникает при анализе резких скачков деформации, исследование релаксации напряжения требует, на наш взгляд, перехода к моделям с включением демпфера последовательно упругим элементам и составит предмет отдельной публикации.

Обсуждение

Полученные в результате математического моделирования кривые гистерезиса соответствуют статической кривой сила–длина с учетом ее нелинейности в определенных условиях. Таким образом, представлено объяснение нелинейной формы петли гистерезиса, наблюдаемой на эксперименте без дополнительных предположений об экспоненциальной зависимости напряжения от деформации.

Раздвижка ветвей широкой части петли гистерезиса в разных диапазонах деформаций соответствует величине вязкости элемента, который вносит основной вклад в той или иной области деформации. В случае, когда параметры жесткости и вязкости первичных элементов существенно различаются (первые, как видно из подписей к рис. 3 и 4 на два порядка, тогда как вторые на порядок), кривая гистерезиса может иметь несимметричный вид с расширением в области или малых, или максимальных деформаций. При этом, на наш взгляд, при описании формы кривой гистерезиса нет необходимости в предположении зависимости параметра вязкости от длины препарата, как это сделано, например, в работе [2].

Установлено, что благодаря наличию параметров модели, описывающих упругость и вязкость элементов, имеется возможность варьирования формы кривой гистерезиса. Поскольку величины этих параметров могут быть оценены при сопоставлении кривых с экспериментальными данными [15], по изменению формы кривой гистерезиса можно судить о соотношении параметров, характерных для тех или иных структур, в реальных образцах мышц и об их изменении в различных условиях.

Неполное соответствие экспериментальных и теоретических данных по форме петли гистерезиса во всем диапазоне деформаций предполагает необходимость введения демпферов в поперечные и наклонные элементы структуры одновременно, а также и в последовательном их соединении. Если предположить, что физическим источником вязкости является фильтрация жидкости, то на основании этого вывода можно сделать предположение о присутствии механизмов фильтрации в миокарде как через мембрану (поперечные элементы), так и межклеточной жидкости (наклонные элементы).

Для большей определенности качественных и количественных выводов при сравнении теории и опыта, необходимо повышение точности эксперимента, которая пока еще недостаточна для оказания предпочтения той или иной модели.

Таким образом, показано, что простейший вариант учета вязкости в рассмотренных ранее двумерных моделях с помощью введения демпферов параллельно первичным упругим элементам позволяет получить нелинейные кривые гистерезиса, наблюдаемые в экспериментах, и кривые релаксации деформации.