Нелинейные колебания цилиндрических оболочек при воздействии температуры

Конструкции в виде замкнутых цилиндрических оболочек широко применяются в различных отраслях промышленности: авиа и космической, судостроении, строительстве. Их использование предполагает воздействие на них различных типов статических, динамических, температурных и других видов нагрузок. При воздействии на замкнутые цилиндрические оболочки возникают теоретически интересные и практически важные задачи статики и динамики. В результате нагружения возникают нелинейные колебания и возможно явление потери устойчивости, приводящее к существенному изменению формы оболочки.

Учитывая современный уровень развития гиперзвуковых технологий на сегодняшний день имеется острая необходимость дальнейшего анализа колебательных процессов в цилиндрических оболочечных системах при воздействии температурных полей и знакопеременных нагрузок. Известно, что аэродинамический нагрев вызывает образование неравномерных полей температуры в конструкциях. Именно с данным фактом связано появление напряжений в цилиндрических оболочках.

Изучение упругих систем при различных воздействиях было начато Лаврентьевым М.А. и Ишлинским А.Ю., а затем продолжено Алфутовым Н.А., Вольмиром А.С., Григолюком Э.И. Фундаментальные исследования в данном направлении получены Ободан Н.И., Вольмиром А.С., Баженовым В.Г. и др. Решения, полученные указанными авторами, выполнены для стационарных задач или для динамики при действии импульса бесконечной продолжительности во времени.

Воздействия периодически меняющихся температур на тонкостенные сосуды, которые имеют одну либо несколько осей симметрии, исследовал Г. Эйхельберг. Кроме этого, Г. Гринберг изучал напряжения, которые возникают в процессе охлаждения сферических поверхностей. Применительно к толстым плитам, цилиндрам и сферам некоторые важные результаты с применением в области бетонного строительства добился Г. Н. Маслов.

Основы теории термоупругости получили значительное развитие из-за необходимости разрешения большого количества проблем в современной технике. Термодинамические обоснования некоторых уравнений общей теории термоупругости, а так же систематизация базовых исследований термоупругих состояний однородного тела имеются так же в трудах Я.С. Подстригача, Б. Боли, В. Новацкого, А. Д. Коваленко, Дж. Уэйнера, монографиях В.Ф. Кириченко и О.О. Евтушенко.

В настоящей статье рассматриваются цилиндрические оболочки, которые находятся под действием внешних знакопеременных нагрузок и температурного поля.

Оболочка является неким реальным объектом, а теория любого реального объекта или явления не может входить в противоречие с законами физики.

Поэтому для сплошных сред, к которым относятся оболочки необходимо полное выполнение уравнений равновесия (движения), неразрывности среды, геометрии перемещений и общих основ термодинамики в каждой внутренней точке оболочки и уравнений равновесия на ее краевых поверхностях.

В рамках классической нелинейной теории цилиндрических оболочек исследуется замкнутая оболочка с круговым сечением определенной длины, характеризующаяся постоянной плотностью в случае действия поперечных знакопеременных нагрузок. Применим систему координат: ось x направляется по продольным координатам, ось у - по окружным координатам, ось z - по нормали к поверхности (рисунок 1).

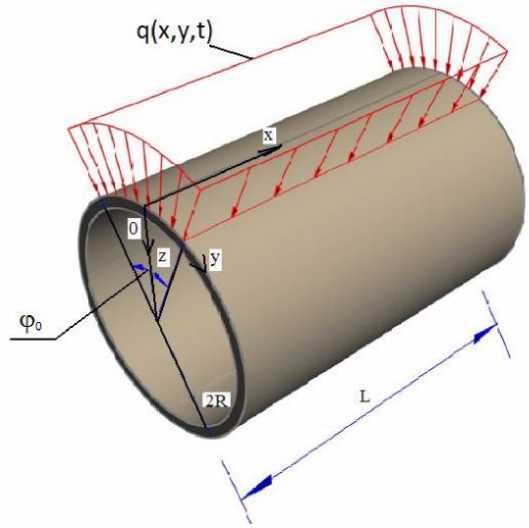
Рисунок 1. Расчетная схема

В работе исследуются колебания шарнирно опертой замкнутой

цилиндрической оболочки, характеризующейся однородными граничными условиями.

Краевая задача по пространственным координатам методом Бубнова-Галеркина в высших приближениях [8] сводится к задаче Коши, которая решается методом Рунге - Кутта 4-го порядка.

Рассматривается характер колебаний оболочки под действием поперечной синусоидальной нагрузки, приложенной по полосе к поверхности цилиндрической оболочки.

Приведем некоторые известные критерии динамической устойчивости. Сунг Т.Т и Рот Д.С. в своей монографии доказали, что нагрузки, при которых начинаются обратные процессы изменения времени, которое необходимо для достижения первого максимума зависимости «нагрузка – время», считаются критическими.

Для исследования динамической потери устойчивости замкнутой цилиндрической оболочки воспользуемся динамическим критерием А.С. Вольмира, где происходит значительное ускорение роста прогиба при малом росте нагрузки либо появляются точки перегиба.

Анализируется зависимость для каждого элемента q₀ из диапазона q₀ е [ 0;0,45 ] и определяется максимальный прогиб в точке (0,5; 0).

Данные результаты приведены на рисунке 2, для более информативного представления о характере колебаний построена «шкала» характера колебаний оболочки, в каждой точке определяется характер колебаний и в зависимости от этого происходит изменение тона.

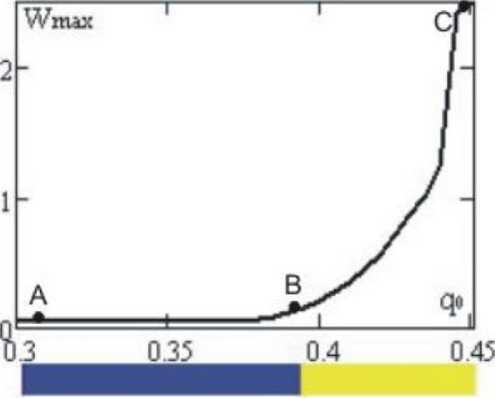
Рисунок 2. Зависимость wmax(q0)

На «шкале» можно видеть, что при изменении q₀ < 0,395 колебания носят один тип - гармонические колебания (черный цвет), а при 0,395 < q 0 < 0,45 характер колебаний изменяется на многочастотный (светло-серый цвет).

Посредствам «шкал» колебаний цилиндрической оболочки имеется возможность отследить процессы переходов колебаний от гармонического вида к хаотическому, а так же определить значения, при которых воздействие знакопеременной нагрузки приводит к необратимым изменениям в оболочке.

Наблюдается динамическая потеря устойчивости, когда небольшое изменение параметра интенсивности нагрузки q 0 приводит к резкому росту прогиба. Исследование зависимости w_max(q₀) для каждого q₀ дает возможность устанавливать зону потери устойчивости систем в случае воздействия знакопеременной нагрузки.

Проанализируем явление утраты устойчивости цилиндрической оболочки. Исследуем характер колебаний в докритическом состоянии при значениях q₀ = 0,31, и q₀ = 0,395 - это точки А и В соответственно, и в зоне потери устойчивости оболочки q₀ = 0,45 - точка С на рисунке 2.

Рассмотрим характер колебаний при значении параметра нагрузки q₀ = 0,31 -это точка А на рисунке 2. Прогиб оболочки во времени на графике сигнала w(0,5;0;t) изменяется периодически, колебания происходят около нулевой отметки.

Рассмотрим характер колебаний в зоне потери устойчивости оболочки (q 0 = 0,45). При изменении параметра нагрузки q₀ = 0,45 характер колебаний резко изменяется, прогиб оболочки и количество пиков увеличивается. Качественно изменяется фазовый портрет, увеличивается количество петель, а сам фазовый портрет приобретает форму аттрактора. Увеличение числа петель характерно для появления новых частот, либо бифуркаций.

Видно, что происходит увеличение вдавливания оболочки в зоне действия нагрузки и расширение оболочки вне зоны действия нагрузки.

Различные нагрузки являются определяющими при расчете новых конструкций, технологических процессов высокотемпературной обработки материалов. Верная оценка прочностных характеристик некоторых конструкций невозможна в принципе, без четкого учета пластического поведения материала, прогибов, взаимодействия конструкций и так далее. Решение данных задач в результате их сложности возможно лишь численными методами на современных электронно-вычислительных установках.

Для решения задачи устойчивости цилиндрических оболочек, находящихся в температурном поле, под действием постоянного давления с учетом геометрической нелинейности предложено проводить исследования методом Бубнова-Галеркина по пространственным координатам в форме В.З. Власова. Метод Бубнова-Галеркина, возникший первоначально как численный метод, в настоящее время является мощным средством исследования проблем разрешимости широкого класса задач математической физики, как стационарных, так и динамических. Данный подход дает возможность привести любую из распределенных систем к виду системы с сосредоточенными параметрами и далее рассматривать данную механическую систему, как совокупность объектов со значительным числом степеней свободы [10].

Геометрическая нелинейность порождается применением нелинейных соотношений между деформациями и перемещениями. Это позволяет учесть влияние изменения формы и размеров конструктивного элемента на его напряженно-деформированное состояние. Если же становится неприемлемым закон Гука, связывающий напряжения и деформации нелинейными соотношениями, то нелинейные зависимости порождают задачу с физической нелинейностью. Если в процессе деформирования конструкции может изменяться её расчетная схема путем разрушения старых и образования новых связей, то имеет место конструктивная нелинейность, присущая конструкциям во время монтажа или изменения режима нагружения. Также нелинейность может проявиться при расчете конструкций, взаимодействующих с окружающей средой.

Существование различных методов отыскания критических состояний цилиндрических оболочек объясняется разнообразием свойств механических систем. Статический подход при изучении устойчивости приводил к тем же результатам, что и более сложный динамический, поэтому имел право на существование в течение длительного времени. Разновидностью статического критерия является энергетический критерий.

Для статического метода определяют, в каких нагрузках для начальной формы равновесия цилиндрической оболочки возникают соседние искривленные формы равновесия бесконечно близкие к её исходной форме. Для такой искривленной формы оболочки составляют дифференциальное уравнение равновесия. Решая его, находят критическое значение нагрузок. Таким образом, задача исследования устойчивости исходной равновесной формы заменяется задачей разыскания точек бифуркаций форм равновесия.

В случае применения энергетического метода производится сравнительный анализ изменений потенциальной энергии и работы сил выпучивании для цилиндрической оболочки. В основе данного критерия заложены фундаментальные принципы механики сплошных сред, а именно:

• -    принцип перемещений;

• -    принцип изменений напряженного состояния.

Согласно условию стационарности полной потенциальной энергии системы, которое следует из принципа перемещений, перемещения, которые удовлетворяют уравнениям равновесия, придают потенциальной энергии стационарные значения. Согласно условию стационарности дополнительной энергии, напряжения, удовлетворяющие уравнениям неразрывности деформации и граничным условиям, придают дополнительной энергии стационарное значение.

Определение величин критических нагрузок замкнутых цилиндрических оболочек, которые находятся в температурном поле, рекомендуется производить по средствам метода установления, впервые использованного В.И. Феодосьевым.

В данном методе, который В.И. Феодосьев определил, как вариационношаговый метод, деформация системы рассматривается, как единый процесс, вне зависимости от скорости изменения внешних сил. С этой целью вводятся независимые переменные и составляются специальные уравнения движения [6].

В некоторых источника этот метод так же называется итерационным методом нелинейных уравнений. Каждый следующий шаг по времени в данном методе -это новое приближение к точному решению поставленной задачи. Данный метод сводится к разрешению задачи Коши для системы дифференциальных уравнений, изначально являющейся линейной относительно времени. Зависимости напряжении от деформации определяется отношениями упругости и пластичности.

Основное достоинство данного рекомендуемого метода - полное стирание границ между линейными и нелинейными системами, малыми и большими передвижениями, статикой и динамикой. В случае применения данного метода практически нет разницы между задачами упругости и пластичности [8].

Подведем итоги статьи. Подробно исследован вопрос о нелинейных колебаниях круговых цилиндрических оболочек. Произведены исследования геометрических нелинейных задач замкнутых цилиндрических оболочек. Исследованы теоретические аспекты возникновения температурных напряжений в цилиндрических оболочках. Проведено исследование колебательного процесса замкнутой цилиндрической оболочки на основе анализа изменения прогиба оболочки во времени. Применен критерий динамической потери устойчивости замкнутых цилиндрических оболочек. Определен общий сценарий переходов колебаний цилиндрических оболочек, которые находятся под воздействием температурных полей.