Нелинейные локализованные продольные магнитоупругие волны в пластине, находящейся в произвольно ориентированном магнитном поле

Создание и развитие теории сопряженных полей различной физической природы во многом стимулировано современными проблемами науки и техники. Одним из интенсивно разрабатываемых разделов этой теории является электромагнитоупругость, изучающая взаимодействие механических и электромагнитных полей в материалах и конструкциях. Теория электромагнитоупругого взаимодействия развивается сегодня по нескольким направлениям. Отметим основные из них:

– магнитоупругость (и магнитотермоупругость) электропроводящих неферромагнитных тел в постоянном внешнем магнитном поле [1, 2];

– магнитоупругость магнитоактивных, в том числе пьезомагнитных,   ферромагнитных   и магнитострикционных сред [3, 4];

– электроупругость пьезоэлектрических и электрострикционных сред [5, 6].

Остановимся на первом из упомянутых направлений. Здесь предполагается, что упругое деформируемое электропроводящее тело находится в начальном постоянном магнитном поле и электромагнитное взаимодействие между телом и полем осуществляется посредством пондеромоторных сил Лоренца, входящих в уравнения движения упругой среды, и обобщенного закона Ома для материальной частицы, движущейся в магнитном поле. В рамках этой теории в [7] изучалось распространение нелинейных магнитоупругих волн. Волна деформации задавалась как продольная, а направление внешнего постоянного магнитного поля полагалось перпендикулярным направлению ее распространения.

В настоящей работе рассматривается распространение нелинейной продольной волны в пластине, находящейся во внешнем постоянном магнитном поле, имеющем произвольную ориентацию в пространстве.

2.    Уравнения магнитоупругости для пластины, находящейсяв произвольно ориентированном магнитном поле

Система динамических уравнений магнитоупругости имеет вид [1, 7]:

д2u                                   1 ,„ p —2 =( X + p) grad div u + pAu + Fнел +   (rot H x H), дt4n

5H     Г du

--= rot —x H +A дt       дт4no

Здесь u — вектор перемещений; X, p — модули упругости (константы Ламе) второго порядка; р — плотность материала; σ — проводимость; с — скорость света в вакууме; H — напряженность магнитного поля. Вектор F _нел. включает в себя слагаемые, обусловленные учетом упругой нелинейности.

В работе [7] выведена основанная на (1) система уравнений магнитоупругости для пластины, совершающей продольные колебания, в предположении, что внешнее постоянное магнитное поле с напряженностью H ₀ перпендикулярно направлению распространения волн. Система уравнений

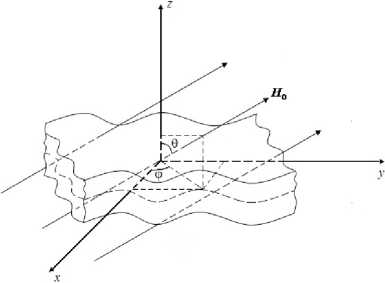
Рис. 1. Пластина в произвольно ориентированном магнитном поле

магнитоупругости сведена к эволюционному уравнению относительно продольной деформации, и исследовано влияние напряженности внешнего магнитного поля на распространение двумерных нелинейных локализованных магнитоупругих волн в пластине.

Рассмотрим случай, когда пластина находится во внешнем постоянном магнитном поле с напряженностью H0 , имеющем произвольную ориентацию в пространстве, которая определяется углами 0< 0 < п, 0< ф <2п, (Рис. 1). Как и в [7], будем полагать, что суммарное магнитное поле состоит из своего постоянного значения H0 = H0n и возмущений, появляющихся в результате взаимодействия начального магнитного поля с полем деформаций: H = H0n + h, где n — нормаль к срединной поверхности пластины, h — вектор малого возмущения магнитного поля. Вектор перемещений, вектор малого возмущения магнитного поля и вектор суммарного магнитного поля имеют следующие компоненты: u = (ux,uy,uz), h = (hx,hy,hz), H = (H0sin9cosф + hx,H0sm9smф + hy,H0cos9 + hz).

Используем идею приведения трехмерных уравнений теории упругости к двумерным уравнениям равновесия или динамики пластин [8], которая заключается в выражении уравнения, описывающего напряженно-деформированное состояние в произвольной точке тела, через новые величины, заданные вдоль срединной поверхности пластины. При этом переход от бесконечного числа степеней свободы к конечному в направлении нормали к срединной поверхности пластины осуществляется путем аппроксимации смещений многочленами. Применяя аппроксимацию вида [7]

u 1 = u ( x , y , t ) , u ₂ = v ( x , y , t ) , u 3 = -X z div V /( X + 2 p ) ,

V ^T = ( u v ) , запишем систему уравнений магнитоупругого равновесия в перемещениях для пластины, находящейся во внешнем постоянном магнитном поле с произвольной ориентацией:

д2u    2 д2u   /2    2) д2v    2 д2u X2h2    Г д4u  + д4v дt2    p дx2   ' 1    т'дxдy   т дy2   3(X + 2p)2 (дx2дt2 дxдyдt2

X ² c ² h ²   Г д ⁴ u д ⁴ u д ⁴ v д ⁴ v )     д u д ² u

⁺—:------ "T I ^{+       +} _ i- ⁺ _ _ i I = ^ai "z— ⁺

3 ( X ₊ 2 p ) (5 x ⁴   д x ² д y ²   д x ³ д y  д x д y ³ J     д x д x ²

+a ₂

д Гдu дv)Гдu дv) д Гдu дv) 2Т-! ^Г + ^Т II ^Г + ^Т I + ^rI ^Г + ^Т I дy ( дy дx J ( дx дy J дx ( дy дx J

+ о^з

дv д2v ---+ дy дx дy

+a 4

д v д ² v    1

д x д x ² 4 пр

( ^H 0 c ^{os 0 +} h z ) | ^h ^ + ( ^H 0 д x ^v

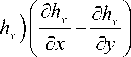
д ² v 2 д ² v /2    ₂\ д ² u ₂ д ² v X ² h² f д ⁴ v д ⁴ u A

~ cp l y? ”⁽ cl - c ^{т )} l У д X ~ c " l x² ~ 3 ( X + 2 ц ) 2 (д y ²d t ^{2 +} д y д x д t ² ) +

X ² c 2 h ² f д ⁴ v    д ⁴ v     д ⁴ u     д ⁴ u A     д v д ² v

+ —------Y ttt ⁺ _ t ⁺ _    ⁺ _ _ i I = ^ai ⁺

3 ( X + 2 ц ) (д y ⁴ д y ² д x ² д y ^Зд x д y д x ³ )     д y д y ²

+а ₂

, д | д v д u 11 д v д u | д ( д v д u |

2 — 1 —+ — II . + . I+ —|    + I дx (дx дy )(дy дx) дy (дx дy )

+ a ₃

д u д ² u

+ д x д y д x

+а ₄

д u д ² u    1

--:--- д y д y ² 4 np

( H 0

cos 6 + h z     ^-( ^H 0

д y

sin 6 cos

-

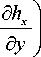
^д H д Yл i \ д ^u (■ a , , \ д v Y c ^{2 f}

—- = — H,, sin6sinф + h--(H,, sin6cosф + h )— +--- дt    дyY 0              y7 дt  V 0                 дt) 4ло( дHy     д Y• л •    , z Adu                    , хбvA

—- =--Hn sin 6 sin ф + h--( Hn Sin 6 COSQ + h ) — at      ax(V 0               y7 at   0 °               ) at)

д ² h_x д ² h_x 1 д x ² д y ² ) ;

c 2 +— 4 n o	f^ h y ( д x 2	д 2 hy д y 2
c 1 f	д 2 h	д 2 h A
	z	+ z
4 n c (	д x 2	д y22 J

;

Здесь c p = c lyj 1 - ( c l ² - 2 c 2 ) y c⁴ — скорость, с которой распространялась бы продольная волна в пластине при отсутствии геометрической дисперсии и взаимодействия с магнитным полем; c l = ^ ( X + 2ц ) /р — скорость распространения продольной волны; c _т = J ц/р — скорость распространения сдвиговой волны; u , v — перемещения срединной поверхности пластины в направлении осей x и y ; h — полутолщина пластины; α₁,α₂,α₃,α₄ — коэффициенты упругой нелинейности.

• 2.    Влияние ориентации магнитного поля на параметры магнитоупругой волны

Повторяя рассуждения, сделанные в случае внешнего постоянного поля, перпендикулярного к направлению распространения волн [7], введем лучевые координаты:

^ = x - с t , n = е x , X = Vs y                                      ⁽⁸⁾

и новые функции:

u = u , v = Vs v ,   h = h , h = Vs h ,   h = Vs h .

zz x     x y     y

Здесь s — малый параметр, ё — некоторый коэффициент, смысл которого покажем позднее. Подставив (8) и (9) в систему (3)–(7), как и в [7], придем к эволюционному уравнению относительно продольной деформации U = д и /д ^, которое объединяет в себе уравнения Кадомцева-Петвиашвили (описывающее нелинейные волны в двумерных средах со слабой дисперсией) и Хохлова–Заболотской–Кузнецова (описывает распространение звуковых пучков конечной амплитуды в нелинейно-диссипативной среде):

дГд U _T U U _од ³ и _тд ² U A д ² U —  +а U + в—_г-5—- +у—-д^ (дп д^ д^ ³ д^ ² ) дх ²

= 0.

Но теперь коэффициенты будут зависеть еще и от углов ориентации магнитного поля 6 и ф :

а =

3 - ( c J ci ) 2 ( cos ² 6 + sin ² 6 sin ² ф ) - ( 6 X ²/ ( X + 2 ц ) ² )( 1 - ( c _т /С) ) ² ) + ( c_p/c_t ) 2 g

в =

2 ^ 2 ( c pj c l ) + ( c A/ c l ) 2 ( cos ² 6 + sin ² 6 sin ² ф ) ]

X ² h ²     ( c p/ c / J^+j c A/ c l ^lfcost ^+ sinl^sin^ ^ l zI c l/ c l ^l

6 ( X + 2 ц ) ²       2 ( c pl c ) ² + ( c A/ c l ) 2 ( cos ² 6 + sin ² 6 sin ² ф )      ,

- 1,

5 =

c ²

,

8 no cl J( cjc ) + ( cAki ) ( cos ² 6 + sin ² 6 sin ² ф )

• ^{1    +} ( ^cA !^ci ) 2 ( ^cos2 ^{6 +} sin ^{2 6} sin ² ф ) - ( ^c т !^ci ) 2 ( ² - ( cp c i ) 2 )

Y =                                                      x

21 2 (epic) +(cAlc )2 (cos2 6 + sin2 6 sin2 ф) I x_____________________________1_____________________________

^[ ( c P / c i ) ^{2 +} ( c A / c i ) ² ( cos ^{2 6 +} sin ^{2 6} sin ² ф ) - ( c т / c i ) ² ]

Здесь g = ( 2 A + 6 B + 2 C )Д р c 2 ) , c A = H ₀ ² /( 4np) — скорость волны Альфвена [9]; c = c²_р + cA — характерная скорость волны, заранее неизвестная; A , B , C — константы упругости третьего порядка (модули Ландау).

В работе [7] методом простейших уравнений [10] найдено точное решение уравнения (10):

U (^, X, n) = -[352/(25ap)] • [1 + th ((k о § + k1X + k 2П)/2 )]2,                         (12)

где k 0 =5/(5 в), k2 =-6 53/(125₽2) + 5pYk/ /5, k 1 — произвольная постоянная. Выражения для амплитуды и ширины волнового пучка (13) вдоль координатных осей имеют вид:

U ₀ =- 35 ² /( 25ав ) , А_; = 10в/3, А_п = 250в 2 /5 3 , А_х = 50^ /( V75 ² ) .

Проследим за изменением амплитуды и ширины пучка в направлении каждой из координатных осей ξ,η,χ, учитывая ориентацию внешнего магнитного поля. Изменение параметров в зависимости от углов рассмотрим при c_A(c_l = 0,2. Выражения для амплитуды и ширины пучка вдоль осей определяются формулами (14), в которых коэффициенты уравнения (10) имеют вид (11). Из соотношений (12) и (13) следует, что ширины волнового пучка вдоль координатных осей являются периодическими функциями углов 6 и ф с периодом п , но, согласно определению произвольно ориентированного вектора внешнего магнитного поля, во внимание принимаются лишь их значения из интервалов 0 < 6 < п , 0 < ф <  2 п .

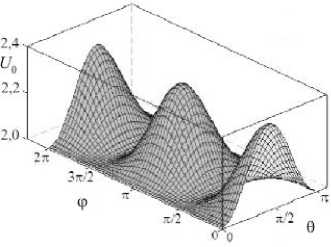
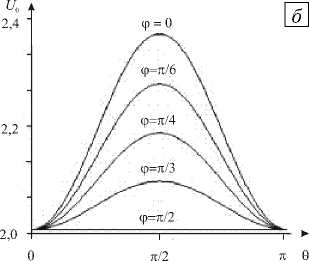
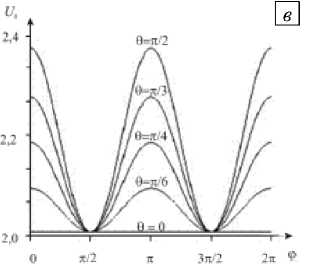
На рисунке 2, а изображена поверхность U ₀ ( ф , 6 ) , которая представляет собой зависимость амплитуды волны от углов 6 и ф , и ее сечения плоскостями ф = const и 6 = const. Из рисунка рисунке 2, б видно, что с ростом угла ф на отрезке [ 0, п/2 ] амплитуда волны убывает. При значениях 6 = 0, п она принимает минимальное значение и не зависит от величины угла ф . При 6 = п/2 амплитуда волны достигает максимального значения. С ростом угла 6 (Рис. 2, в ) на отрезке [ 0, п/2 ] амплитуда волны возрастает и становится максимальной при ф = 0, п . При углах ф = п/ 2 и ф = 3п/2 амплитуда минимальна и не зависит от величины угла 6 .

а

Далее на рисунке 3 приведены результаты анализа зависимостей ширины волнового пучка в направлении лучевых координатных осей.

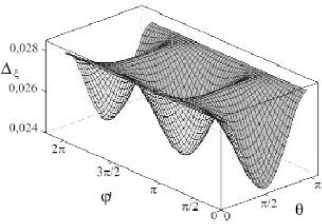
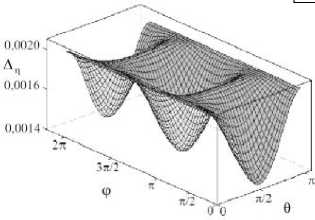
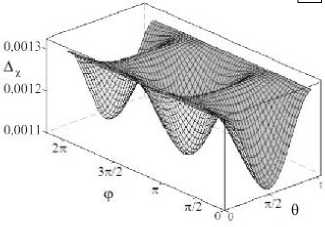
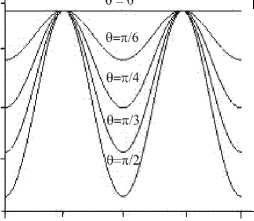
На рисунке 3, а , г , ж изображены поверхности А ^ ( ф , 9 ) , А _п ( ф , 9 ) и А _х ( ф , 9 ) , которые представляют собой зависимости от углов 9 и ф ширины волнового пучка, соответственно, в направлении осей ^, n, X ■ В среднем столбце (Рис. 3, б , д , з ) показаны сечения этих поверхностей плоскостями ф = const. Как видно из рисунков, с ростом угла ф на отрезке [ 0, л/2 ] ширина волнового пучка в направлении каждой из осей возрастает. При значениях угла 9 = 0, л она достигает максимального значения и не зависит от величины угла ф . При 9 = л/2 ширина волнового пучка становится минимальной.

Правый столбец содержит сечения поверхностей А_? ( ф , 9 ) , А _п( ф , 9 ) и А _х ( ф , 9 ) плоскостями 9 = const. Из анализа линий уровня, лежащих в этих сечениях, можно заключить, что с ростом угла 9 на отрезке [ 0, л/2 ] ширина волнового пучка убывает, а при изменении угла ф принимает свое минимальное значение при ф = 0 и ф = л . Ширина пучка вдоль соответствующей оси при ф = л/ 2 и ф = 3 л/ 2 максимальна, и это значение (разное для каждой из лучевых осей) не зависит от угла 9 .

В отличие от амплитуды, ширина пучка вдоль координатных осей принимает минимальные значения там, где амплитуда максимальна и, наоборот, максимальна при значениях углов, соответствующих минимальным значениям амплитуды.

Проведем относительное сравнение степени влияния ориентации и напряженности магнитного поля при его поперечной по отношению к направлению распространения волны ориентации на характеристики

а

0,026

I А-0,028

Ф=л/2

б

4)=л/3/

в

0,0016

0,024 Т 0

I Л" 11,0020 "

л/2 (р=л/2

(p=7t/3

ж

0,0012 -

0,0014 + 0 Ду 0,0013 ■

0,0014

л/2        л Зл/2

Зл/2 2л Ф

и

9 = 0

л/2

Д, 0,0013

0,0012

е=л/з.

.0=л/2;

0,0011 +■ о

0,0011

Рис. 3. Поверхности А ^ ( ф ,0 ) ( а ), А_л ( ф ,9 ) ( г ), и А_х ( ф ,9 ) ( ж ) и их сечения плоскостями ф = const и 9 = const

Зл/2      2 л Ф

решения (12) уравнения (10) (см. Табл.). Здесь ∆ U ₀ , ∆ Δ _ξ , ∆ Δ _η , ∆ Δ _χ — величины абсолютного изменения амплитуды и ширины волнового пучка (решение (12) уравнения (10)) вдоль соответствующих координатных осей в двух ситуациях: магнитное поле характеризуется переменной напряженностью и имеет постоянную поперечную ориентацию по отношению к направлению распространения волны (Решение 1); магнитное поле постоянной напряженности меняет ориентацию в интервале [ 0, 2 π ] (Решение 2). Отношение величин абсолютного изменения характеристик достигает почти 27%.

Таблица. Абсолютные значения характеристик магнитоупругой волны в зависимости от ориентации и напряженности магнитного поля

Характеристики волны	Решение 1 (изменяющаяся напряженность и постоянная ориентация)	Решение 2 (постоянная напряженность и изменяющаяся ориентации)	Отношение Решения 1 к Решению 2, %
∆ U 0	1,5000	0,4000	26,6700
∆ Δ ξ	0,0300	0,0040	13,3300
∆ Δ η	0,0080	0,0006	7,5000
∆ Δ χ	0,0025	0,0002	8,0000

Работа выполнена при финансовой поддержке РФФИ (проект № 12-08-00888) и ФЦП «Научные и научно-педагогические кадры инновационной России» (2009–2013 гг.).