Нелинейные режимы конвекции бинарной смеси в двухслойной пористой среде различной конфигурации

Другим распространенным способом представления неоднородной пористой среды служит система слоев, имеющих различные значения пористости и проницаемости, причем эти свойства в каждом отдельном слое однородны [12–17]. В работе [18] проведено прямое численное моделирование концентрационной конвекции в насыщенной жидкостью пористой среде с анизотропной проницаемостью, которая характеризуется отношением значений проницаемости поперек и вдоль исследуемой области. Для значительного слоистого образования в [19] случайным образом генерируются гетерогенные пористые среды, представляющие ламинированную структуру, в которой горизонтальная корреляционная длина поля проницаемости намного больше, чем вертикальная (поле проницаемости выражается характеристическим постоянным значением и случайной функцией Гаусса). Авторами показано, что ламинированные структуры ограничивают взаимодействие между нисходящими потоками более тяжелой жидкости, то есть оказывают тормозящее влияние на конвекционный поток.

Решение таких задач требует топографических и геологических данных, но зачастую проводится в отсутствие тепловой конвекции или в предположении однокомпонентности или однофазности жидкости [13, 15, 20, 21]. Однако жидкости и газы, насыщающие пористые среды, обладают сложным составом. Это приводит к необходимости учета эффектов диффузии, термодиффузии и другого [22–24].

Целью настоящей работы является моделирование конвекции бинарной смеси жидких углеводородов (тетралина и додекана), взятых в равных долях [25], в двухслойной пористой среде, слои которой имеют разные проницаемости и разделены либо плоской горизонтальной границей, либо границей, имитирующей синклинальную геологическую складку.

Рассмотрим смесь взятых в равных долях додекана (C 12 H 26 ) и тетралина (C 10 H 12 ). За примесь в этой смеси примем более легкий компонент тетралин, а растворителем назовем более тяжелый додекан. Будем считать, что плотность смеси линейно зависит от температуры T и концентрации примеси C :

P = p 0 ( 1 -Р T ( T - T o ) -Р C ( C - C 0 ) ) . (1)

Здесь: Р_г = —— — ^т    P o а т

C

коэффициент теплового расширения; в _C

1 др

P o д C т

коэффициент

концентрационного расширения; р0, C0 и Т0 — средние значения плотности, концентрации примеси и температуры.

Смесь заполняет вытянутую в горизонтальном направлении прямоугольную область пористой среды со сторонами L = 200 м и H = 100 м ( L = 2 H ) и твердыми, непроницаемыми для вещества внешними границами. Расчетная область состоит из двух горизонтальных слоев c разными постоянными значениями проницаемости K ₁ и K ₂ , но одинаковыми прочими свойствами. Исследуем два варианта формы границы Г между слоями: плоскую границу, делящую область на два слоя равной высоты (Рис. 1 а ), и границу в форме дуги окружности радиусом 187,5 м, направленной выпуклостью вниз, что имитирует границу синклинальной геологической складки (Рис. 1 б ).

Рис. 1. Геометрия задачи: система слоев равной высоты ( а ); система, имитирующая синклинальную складку, ( б )

Моделирование термоконцентрационной конвекции бинарной смеси в пористой среде осуществим в рамках нестационарных нелинейных уравнений Дарси–Буссинеска [7] с учетом эффекта термодиффузии. Эти уравнения имеют вид:

0 = - ± VPi-^- V,- g (в T (T - T, ) + в C (Ci- C0)),(2)

p0

(pc)-^ + (pc) Vi -VT =KV2T,(3)

d t

SC., e    i- + Vi-V Ci =D V2 Ci + C0 (1 - C0) DT V2 Ti,(4)

∇⋅ V _i = 0 .

Здесь: V — скорость фильтрации; p — давление; g — ускорение свободного падения; t — время; K ₁ и K ₂ — проницаемости верхнего и нижнего слоев; ν — кинематическая вязкость смеси; λ^∗ — эффективная теплопроводность пористой среды; ( ρ c )^∗ — эффективная теплоемкость пористой среды; ( ρ c ) — теплоемкость смеси; ε^∗ — пористость; D — коэффициент молекулярной диффузии смеси; D_T — коэффициент термодиффузии; индекс i = 1,2 указывает на соответствие верхнему или нижнему слою. Уравнения записаны в предположении постоянства вязкости и коэффициентов переноса и пренебрежении эффектами бародиффузии и диффузионной теплопроводности.

На всех внешних границах поставим условия непроницаемости и отсутствия диффузионного потока вещества, на верхней и нижней границах зададим разные постоянные температуры T_в и T_н ( T_в < T_н ), на вертикальных — отсутствие потока тепла; на границе Γ между слоями — равенство давлений, потоков температуры и диффузионных потоков вещества:

x = 0, L :

V ix = 0,      ∂ ^{T i} = 0,

∂ x

y = 0:

V 2 y = 0,

т = т

T ₂ = T_н ,

V 1 y = 0,

т = т

T ₁ = T_в ,

∂ C ₂ ∂ y ∂ C ₁ ∂ y

-

∂ C i _{= 0,} ∂ x

∂ T 2 _{= 0 ,} ∂ y

∂ T 1 _{= 0,} ∂ y

∂ T ₁ = ∂ T ₂ ∂ ( C 1 - T 1 ) = ∂ ( C 2 - T 2 ) ∂ n ∂ n       ∂ n ∂ n

В начальный момент времени жидкость считаем неподвижной, концентрацию примеси в области — однородной, температуру — линейно зависящей от вертикальной координаты. Разность температур на внешних горизонтальных границах возьмем соответствующей средней величине геотермального градиента: 3 ⋅ 10 ^{- 2} К/м [26]. Используемое в моделировании значение T ₀ = 353, 5 К является средней температурой на глубине залегания нефти в 2 000 м при среднем геотермальном градиенте.

Значение пористости в обоих слоях примем равным ε= 0,1 . Предварительные расчеты показали, что конвекция в однослойной прямоугольной области высотой H при нагреве снизу для смеси тетралина и додекана возникает при Ra ≈ 0,3 , где Ra = Kg β _T H ∆ T у ( a ν ) — аналог числа Релея для пористой среды. Эти расчеты проводились для следующих безразмерных параметров: отношения разделения ψ= C 0 ( 1 - C 0 ) β c D T у ( β _TD ) = 0,694 и числа Льюиса Le =χ/ D = 150 , которые соответствуют рассматриваемой смеси тетралина и додекана. Критическое значение числа Релея, полученное при однослойной конфигурации расчетной области с аналогичными перечисленным выше параметрами, определяет пороговую проницаемость среды, равную 2 ⋅ 10 ^{- 14} м². В настоящей работе расчеты выполнены для следующих значений проницаемости слоев: 10 ^{- 11}; 5 ⋅10 ^{- 12}; 10 ^{- 12}; 10 ^{- 13} м². Такие свойства среды характерны, например, для мелкозернистого песка, песчаника, сланцев [27, 28]. Таким образом, апробированы сочетания проницаемостей слоев, при которых их отношение γ= K ₁ K ₂ принимало значения: 10 ^{- 2}; 10 ^{- 1}; 0,2 ⋅ 10 ^{- 1}; 10¹; 5 ⋅ 10¹; 10².

Используемые для расчетов тепловые и физические свойства смеси тетралина и додекана представлены в таблице. Как видно, коэффициенты термодиффузии и концентрационного расширения выбранной смеси положительны, поэтому при подогреве снизу под действием эффекта термодиффузии более легкий компонент смеси накапливается возле нагретой нижней границы области, а тяжелый компонент — у холодной верхней границы. Таким образом, термодиффузия вызывает дополнительную неустойчивую стратификацию по плотности, приводящую к понижению порога возникновения неустойчивости по сравнению с порогом термогравитационной конвекции.

Таблица. Физические свойства смеси тетралина (50%) и додекана (50%) [29]

ρ 0 , кг/м3	ν , м2/с	χ , м2/с	β T , 1/К	β C	D , м2/с	DT , м2/(с∙К)
840,70	1,81∙10–6	9,70∙10–8	8,95∙10–4	2,70∙10–1	6,46∙10–10	5,94∙10–12

Рассматриваемые механизмы (вязкий, тепловой и диффузионный) имеют разные временные масштабы: соответственно t_v ~ H ²/v , т _х ~ H ²/х , т D ~ H ²/ D . Для принятых в расчетах значений параметров эти времена могут быть оценены как τ_ν ≈2 ⋅10² год, τ_χ ≈ 3 ⋅ 10³ год и τ _D ≈5 ⋅10⁵ год. В настоящей работе вычисления выполнены до времени τ _D , однако на графиках приведены данные до τ _D 5 , до которого наблюдались основные изменения характеристик течения.

Вычисления осуществлялись в программном пакете ANSYS Fluent, реализующем метод конечных объемов. Использовалась равномерная по пространству сетка с квадратными ячейками, шаг сетки составлял 2 м. Для получения дискретного аналога уравнений применялись схемы второго порядка аппроксимации по времени и третьего по пространству. Необходимо отметить, что в программном пакете ANSYS Fluent функция тока Ψ вводится как ρ u = ∂Ψ ∂ y , ρ v = -∂Ψ ∂ x , где u и v — x , y -компоненты вектора скорости, поэтому приведенные здесь данные для функции тока имеют размерность [кг/(мс)].

• 3.    Численные результаты

  • 3.1.    Плоская граница между слоями, γ<1

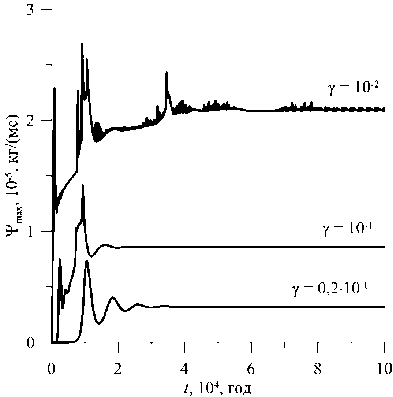
Рассмотрим случай области, состоящей из двух горизонтальных слоев пористой среды равной высоты со значением проницаемости K ₁ = 10 ^{- 13} м² в верхнем слое, а в нижнем проницаемость такова, что K ₂ > K ₁ и γ= K ₁ K ₂ < 1 . Как видно из рисунка 2 а , с уменьшением отношения проницаемостей (ростом проницаемости нижнего слоя) интенсивность возникающего течения увеличивается. При близких значениях проницаемостей в слоях ( γ =10 ^{- 1} или больше) в области устанавливается стационарное течение. При сильно различающихся проницаемостях ( γ =10 ^{- 2} ) наблюдаются сложные квазипериодические колебания (Рис. 2 в ). При этом на начальном этапе имеет место достаточно длительный бесконвективный период, когда значение функции тока близко к нулю. Зарождение конвекции сопровождается скачком интенсивности течения (см. первые пики на графике временной эволюции ψ( t ) , Рис. 2 а ). Далее на графиках ψ ( t ) присутствует еще несколько пиков, которые соответствуют перестройкам структуры течения. Во время бесконвективного периода в области происходит разделение компонентов смеси — растет разность концентраций ∆ C между срединными точками верхней и нижней границ области (Рис. 2 б ).

а

б

6 п

Л104, год

2,24 ~|

^-JllllllljlJI

1,96--1--------------- 1--------------- 1---------------1---------------1---------------1

9,4             9,6             9,8              10

t, 10⁴, год

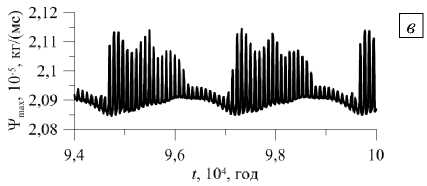
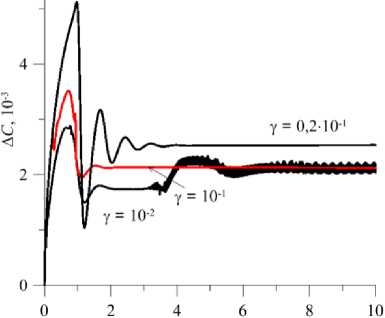
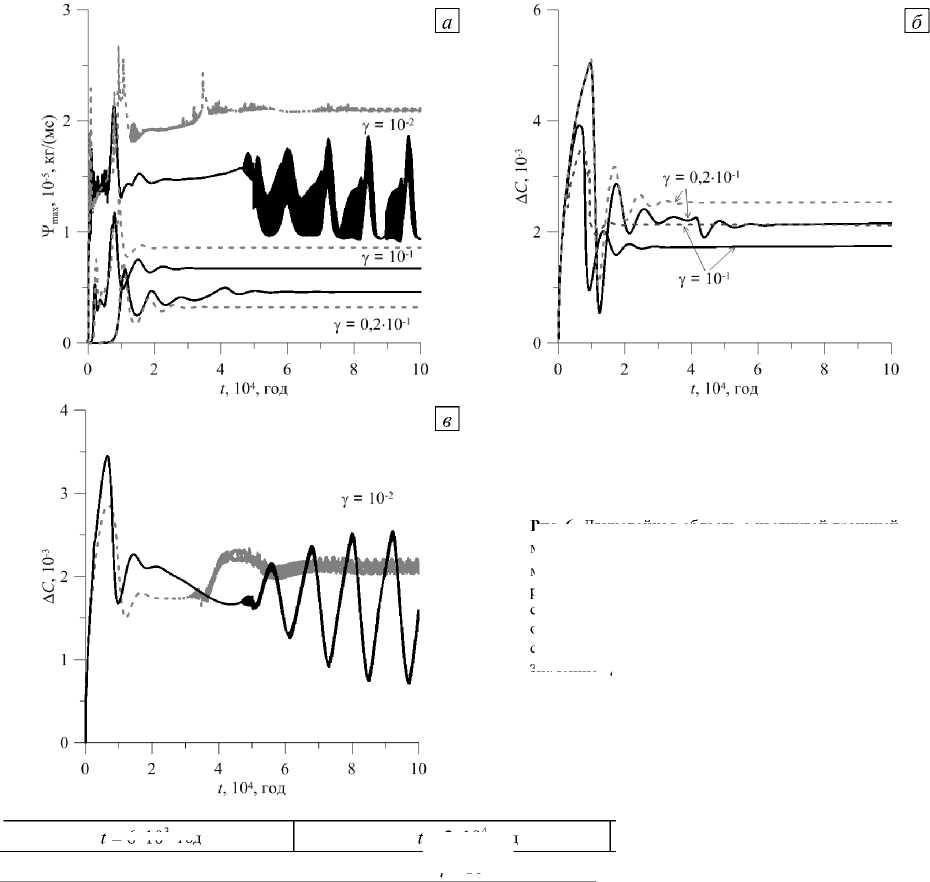
Рис. 2. Двухслойная область с плоской границей между слоями, γ< 1 : временная эволюция максимального значения функции тока ( а ), разности концентраций примеси ( б ), максимального значения функции тока ( в ) и разности концентраций примеси ( г ) в течение нескольких периодов установившихся колебаний; разность параметров рассматривается между срединными точками верхней и нижней границ расчетной области; графики ( в , г ) отвечают проницаемости слоев γ= 10 ^{- 2}

Возникающая конвекция способствует перемешиванию смеси, поэтому на графиках после монотонного роста величины A C , соответствующего чисто диффузионному разделению смеси на начальном этапе, наблюдается резкое падение разности концентраций, а затем колебательное изменение этой величины со временем. На рисунке 2 г показано несколько периодов установившихся колебаний разности концентраций при у = 10 - 2 .

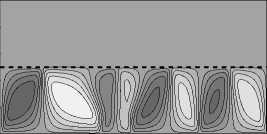
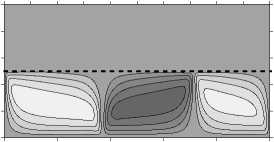
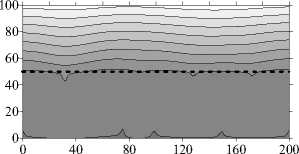
Рассмотрим формирование структуры течения. При значительной разности проницаемостей слоев (у = 10 - 2 ) течение зарождается в нижнем слое — слое с большим значением проницаемости («локальное» возникновение конвекции [7, 30, 31]) и имеет многовихревую несимметричную форму (Рис. 3 а ). Распределение концентрации на малых временах (Рис. 3 б , t = 6 •Ю³ год) практически линейно в верхнем слое и близко к однородному распределению в нижнем. С течением времени число вихрей сокращается сначала до трех, затем до двух (Рис. 3 а , год и t = 10 5 год), а характер изолиний концентрации свидетельствует о слабом проникновении течения в верхний слой. В нижней части слоя распределение концентрации по-прежнему остается близким к однородному, небольшие градиенты концентрации наблюдаются возле границ области и в зонах соприкосновения вихрей. Необходимо отметить, что для этого случая характерно не только «локальное» формирование конвекции на начальном этапе. Даже в установившемся режиме течение носит «локальный» характер: оно существует только в слое с бóльшей проницаемостью.

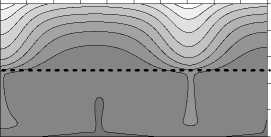
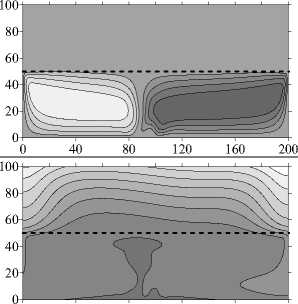
При уменьшении проницаемости нижнего слоя на ранних временах течение снова несимметричное многовихревое, сосредоточенное в более проницаемом нижнем слое (Рис. 3 в , t = 6 - 10³ год). С выходом на стационарный режим число вихрей сокращается до двух, тоже несимметричных, и происходит существенное проникновение течения в верхний слой (Рис. 3 в , t = 10 5 год). Соответственно, на малых временах в верхнем слое изолинии концентрации слабо изогнуты, а в нижнем слое неоднородность концентрации достаточно мала (Рис. 3 г , t = 6 - 10³ год). С установлением течения изолинии концентрации значительно искривляются во всей области (Рис. 3 г , t = 10 5 год).

При близких значениях проницаемостей слоев (у = 0,2 • 10 ^{- 1}) течение возникает и существует во всей области («крупномасштабная» конвекция), но наибольшей интенсивностью оно характеризуется в нижнем слое. Вследствие длительного бесконвективного начального периода во всей области наблюдается близкое к линейному распределение примеси (Рис. 3 е , t = 6 •Ю³ год). В дальнейшем устанавливается четырехвихревое течение, которому отвечают значительно искривленные изолинии концентрации (Рис. 3 д , е , t = 10 5 год).

t = 6 •Ю ³ год

t = 2 •Ю ⁴ год

t = 10 5 год

Y = 10 ^{- 2}

0       40      80      120     160     200

0       40      80      120     160     200

0       40      80      120     160     200

0       40      80      120     160     200

Y = 10 ^{- 1}

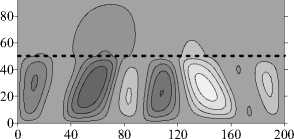
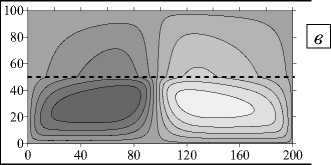
Рис. 3. Двухслойная область с плоской границей (штриховая линия) между слоями, у <  1: поля функции тока ( а , в , д ) и распределения концентрации примеси ( б , г , е ) при разном отношении проницаемостей слоев у ; светлый (темный) оттенок соответствует бóльшему (меньшему) значению параметра

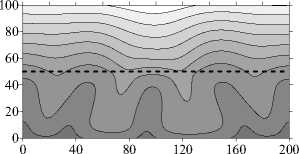
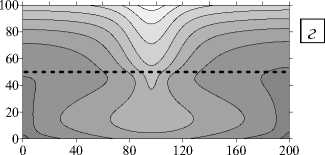
Y = 0,2 - 10 - ¹

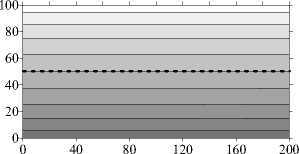
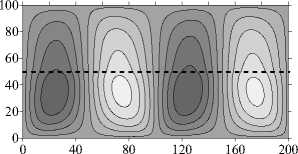
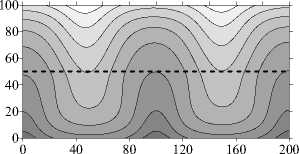
Рис. 3. Продолжение

• 3.2.    Плоская граница между слоями, γ>1

Рассмотрим область, включающую горизонтальные слои равной высоты со значением проницаемости К 2 = 10 ^{- 13} м² в нижнем слое и К 1 >  К ₂ в верхнем слое, при этом у = К 1 / К ₂ >  1, то есть с обратным относительно случая из раздела 3.1 значением у . Как видно из рисунка 4, при близких значениях проницаемостей (у = 10¹ и у = 5 • 10¹) интенсивность течения (Рис. 4 а ) и разделение компонентов смеси (Рис. 4 в ) не изменяются в зависимости от того, какой из слоев более проницаем. Однако в случае большого значения у в области возникают квазипериодические колебания сложной формы, отличной от наблюдаемой при обратном значении у (у = 10², Рис. 4 б , г ). Как видно из рисунка 4 б , при у = 10² (черная кривая) средняя интенсивность течения ниже, а период колебаний значительно больше, чем для у = 10 ^{- 2} (серая кривая). Времена зарождения конвективного течения при этом совпадают, а значения разности концентраций между срединными точками верхней и нижней границ, около которых происходят колебания, достаточно близки (Рис. 4 г ). Последнее может объясняться сформировавшейся структурой течения, а значит и распределением концентрации примеси.

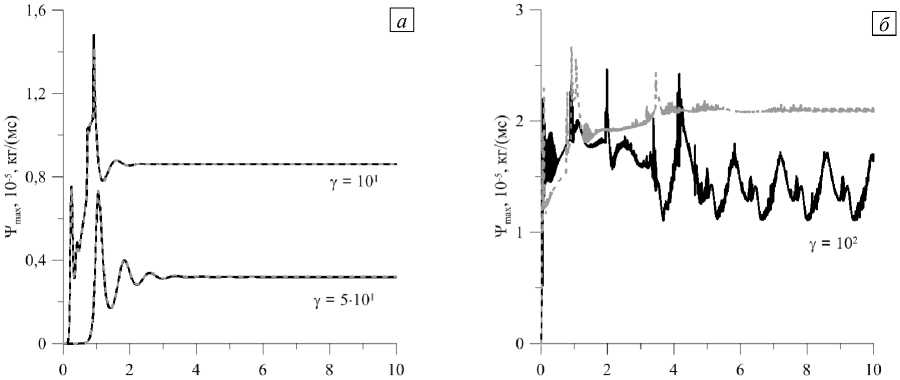
Рис. 4. Двухслойная t, 104, год область с плоской t, 104, год границей между слоями, у > 1: временная эволюция максимального значения функции тока (а), (б) и разности концентраций примеси между срединными точками верхней и нижней границами области (в), (г); серые штриховые кривые отвечают случаю с обратным значением у (см. Рис. 2)

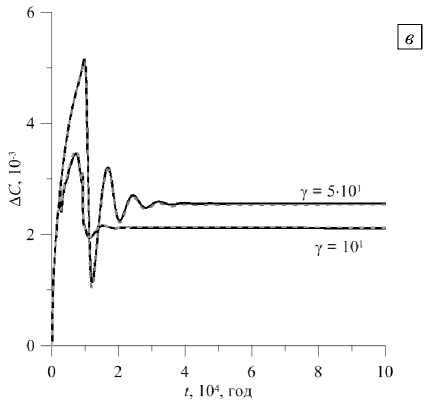
Рис. 4. Продолжение

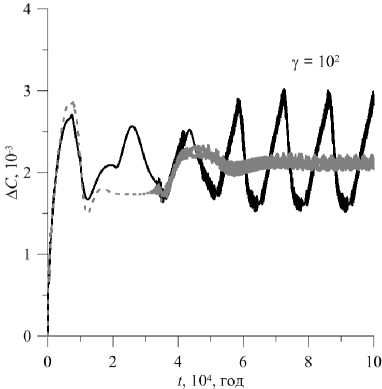
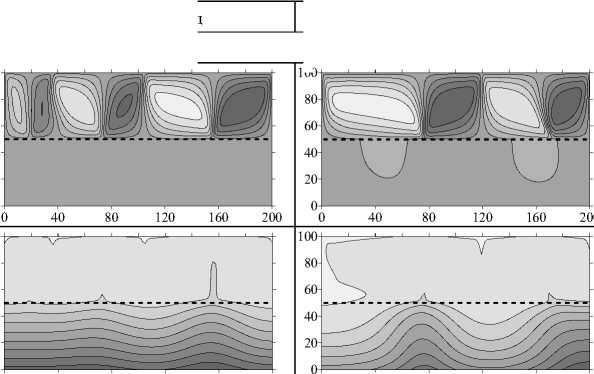
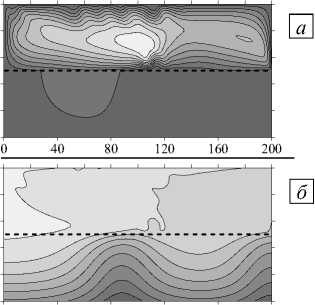
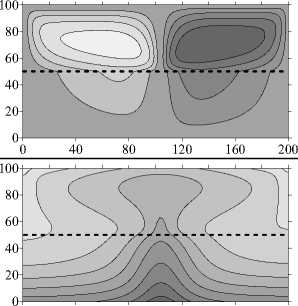
Для больших значений отношения проницаемостей течение в области возникает «локальным» образом в верхнем слое с большей проницаемостью. Для у = 10 2 (Рис. 5) на малых временах наблюдается формирование многовихревого несимметричного течения (Рис. 5 а , t = 6 - 10 3 год). Число вихрей на этом этапе меньше, чем для случая c обратным у (см. Рис. 3 а , t = 6 - 10 3 год). Так же, как и для у <  1, здесь в более проницаемом слое распределение концентрации практически однородно, а в менее проницаемом слое изолинии концентрации искривлены слабо (Рис. 5 б , t = 6 - 10³ год). С течением времени число вихрей сокращается до одного, но проникновение конвекции в нижний слой незначительно (Рис. 5 а , t = 2 - 10 4 год, t = 10 5 год). Сравнение установившихся полей концентрации для у = 10 ^{- 2} и у = 10 2 (Рис. 3 б и 5 б , t = 10 5 год) показывает, что изолинии изогнуты сильнее в менее проницаемом слое в случае K 1 >  K 2 . Это объясняется большим проникновением течения в слой с меньшим значением проницаемости.

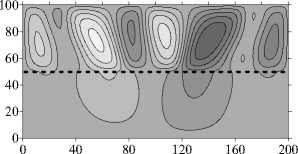
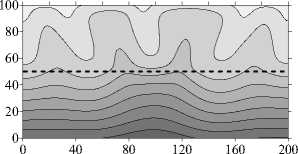
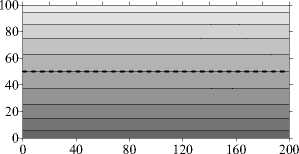
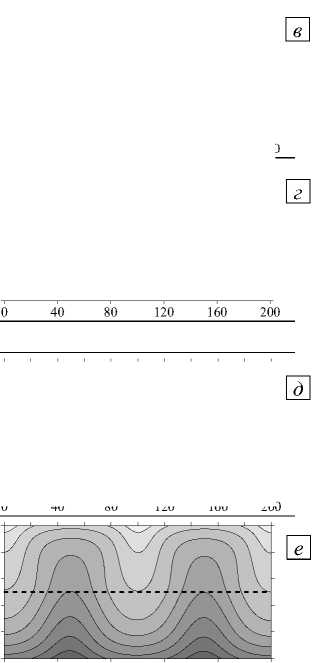
При уменьшении у до значений 10¹ и 5 - 10¹ в области наблюдаются течения, аналогичные случаю обратного значения у с точностью до симметрии относительно границы слоев (Рис. 3 в - е и 5 в - е ). С ростом проницаемости нижнего слоя увеличивается степень диффузии течения в этот слой, вплоть до того, что при у = 5 -10 1 течение занимает уже всю область, хотя наибольшую интенсивность имеет в более проницаемом (верхнем) слое.

t = 6 -103 год t = 2 -104 год у = 102

0      40      80     120     160     200

0      40      80     120     160     200

t = 10 5 год

0       40      80      120     160     200

Рис. 5. Двухслойная область с плоской границей (штриховая линия) между слоями, у >  1: поля функции тока ( а , в , д ) и распределения концентрации примеси ( б , г , е ) при разном отношении проницаемостей слоев у; светлый (темный) оттенок соответствует большему (меньшему) значению параметра

Y = 10¹

–

–

Y = 5 - 10¹

–

–

0       40      80      120     160     200

Рис. 5. Продолжение

• 3.3.    Изогнутая граница слоев, γ<1

Рассмотрим нелинейные режимы конвекции смеси тетралина и додекана в конфигурации с границей слоев, имитирующей синклинальную складку (Рис. 1 б ) и сравним их со случаем плоской границы. В целом, как и в ранее описанных случаях, при близких проницаемостях слоев в области возникает стационарный режим, а при значительно отличающихся проницаемостях — сложное колебательное движение (Рис. 6). При этом для у = 10 - 2 и у = 10 ^{- 1} и изогнутой границы слоев установившееся течение менее интенсивно, в то время как для у = 0,2 -10 ^{- 1} его интенсивность выше, чем для случая плоской границы (Рис. 6 а ). Соответственно, имеет место большее разделение компонентов смеси при значительной разности проницаемостей слоев, которое понижается вместе с ее уменьшением (Рис. 6 б , в ).

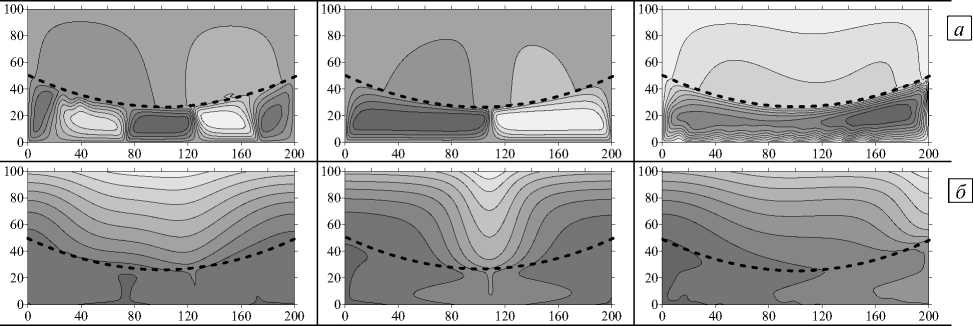
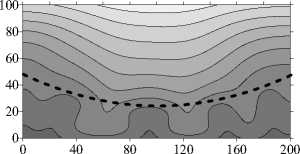
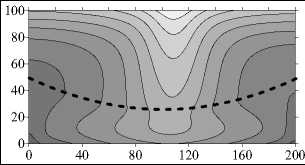
Изогнутая граница раздела слоев в значительной мере меняет структуру установившегося течения и степень его проникновения в верхний слой — в слой с меньшей проницаемостью. Однако на небольших временах структура течения и распределение концентрации примеси в целом похожи на те, что наблюдаются при плоской границе слоев. Так, для у = 10 ^{- 2} на малых временах в нижнем слое формируется пятивихревое течение (Рис. 7 а , t = 6 - 10 3 год), тогда как в случае плоской границы в этот же момент времени течение состоит из 8 вихрей (Рис. 3 а ). В дальнейшем при установлении течения число вихрей сокращается сначала до двух, затем до одного (Рис. 7 а , t = 2 - 10 4 год, t = 10⁵ год). Структура течения несимметрична. Сравнение степени искривленности изолиний концентрации примеси, представленных на рисунках 3 б и 7 б , говорит о менее интенсивном течении (меньшем перемешивании) в нижнем слое и большем проникновении течения в верхний слой.

При увеличении проницаемости верхнего слоя до такой степени, что у становится равной 10 ^{- 1}, структура течения качественно не меняется ни на малых временах, ни в установившемся режиме. При изогнутой границе, как и в плоском случае, в нижнем слое образуется несколько вихрей, число которых затем сокращается до двух (Рис. 3 в , 7 в ). Наблюдаемое при этом пальцеобразное распределение концентрации характерно для много- и двухвихревого течения (Рис. 7 г ).

t = 6 - 103 год t =105 год

Рис. 6. Двухслойная область с изогнутой границей между слоями, у <  1: временная эволюция максимального значения функции тока ( а ) и разности концентраций примеси между срединными точками верхней и нижней границ области ( б ), ( в ); серые штриховые кривые отвечают случаю плоской границы слоев и тому же значению у, что и на рисунке 2

t = 2 - 10 4 год

Y = 10 ^{- 2}

Y = 0,2 - 10 - ¹

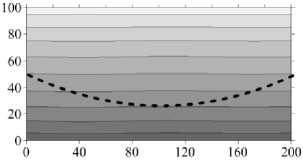
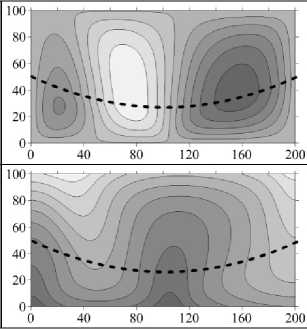
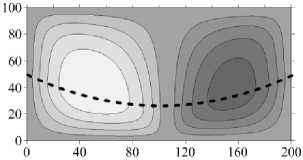
д

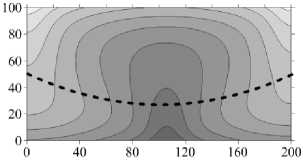
е

Рис. 7. Продолжение

Дальнейшее увеличение проницаемости верхнего слоя приводит к возникновению «крупномасштабного» течения (Рис. 7 д ). В отличие от плоской границы слоев, при изогнутой границе в начальный момент времени зарождается не четырехвихревое симметричное течение, а трехвихревое несимметричное. Затем число вихрей сокращается до двух и сохраняется небольшая асимметрия. Эта асимметрия прослеживается и в распределении концентрации тетралина (Рис. 7 е ).

• 3.4.    Изогнутая граница слоев, γ>1

Последний из рассмотренных случаев соответствует системе слоев с изогнутой границей между ними и значением проницаемости К 2 = 10 ^{- 13}м² в нижнем слое и К 1 >  К ₂ в верхнем слое, так что Y = К 1 / К ₂ >  1. Как видно из рисунка 8, где приведена временная эволюция характеристик течения при этих проницаемостях и для сравнения представлены графики в случае у <  1, как и при плоской границе между слоями, качественные различия в поведении интенсивности течения и разделении смеси наблюдаются только при значительной разнице проницаемостей слоев. Для у = 10 2 происходит быстрое установление нерегулярных колебаний, а для меньших значений у течение по-прежнему выходит на стационарный режим. Для у = 10¹ режим устанавливается очень медленно, на длительных временах сопровождается перестройкой структуры течения и скачком его интенсивности. При более проницаемом верхнем слое количественно интенсивность установившегося течения ниже для небольшой разности в проницаемости слоев (Рис. 8 а , у = 10¹, у = 5 -10¹) и выше, если проницаемости существенно разные (Рис. 8 а , у = 10 2 ), чем в случае у< 1. Соответственно, чем ниже интенсивность течения, тем больше разделяются компоненты смеси (Рис. 8 б , у = 10¹, у = 5-10¹). Для у = 10 2 на рисунке 8 в видно, что средняя величина A C в установившемся режиме практически совпадает с той, что наблюдается при у = 10 ^{- 2}, то есть не зависит от того, который из слоев более проницаем. По-видимому, на это оказывает влияние структура сформировавшегося течения.

Сравнение рисунка 8 с 4-м рисунком показывает, что влияние степени проницаемости слоев при изогнутой границе между ними оказывается более существенным. Так, при плоской границе (то есть при равенстве площадей поперечных сечений слоев) и небольшой разности проницаемостей изменений в интенсивности течения и разделении компонентов смеси не наблюдается. В отличие от этого, при изогнутой границе интенсивность течения и разделение компонентов смеси меняется в зависимости от отношения проницаемостей слоев, поскольку в более проницаемом слое площадь другая.

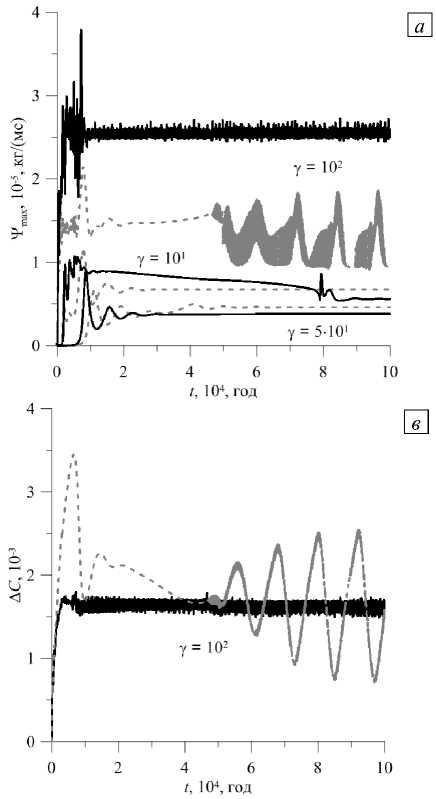
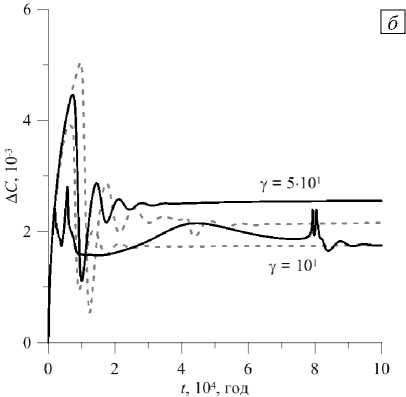
Рис. 8. Двухслойная область с изогнутой границей между слоями, у >  1: временная эволюция максимального значения функции тока ( а ) и разности концентраций примеси между срединными точками верхней и нижней границ области ( б ), ( в ); серые штриховые кривые отвечают случаю при обратном значении у (см. Рис. 6)

t = 6 - 10 3 год

t = 6 - 10 4 год

t = 10 5 год

Y = 10 2

Y = 10¹

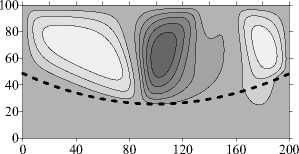
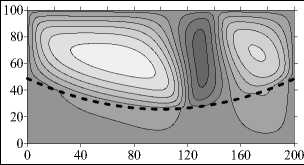
0       40      80      120     160     200

в

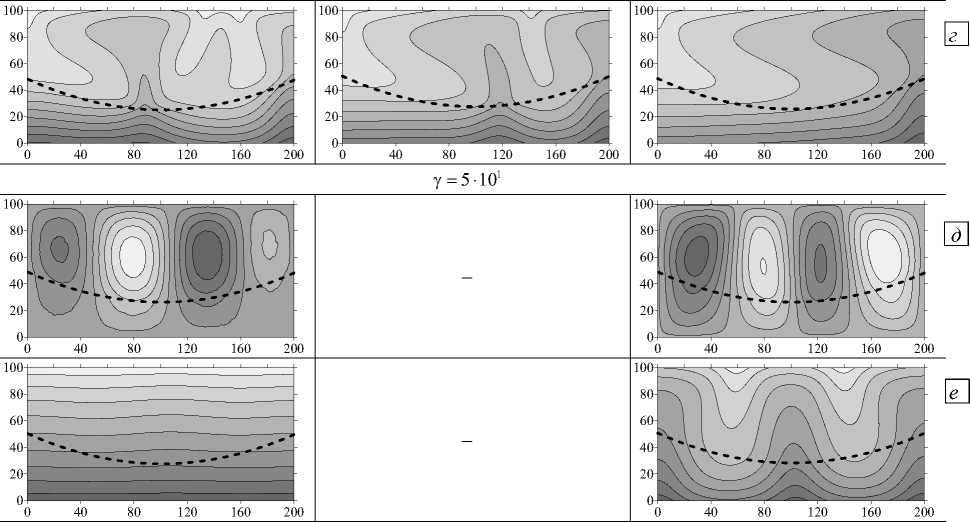
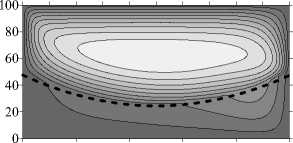
Рис. 9. Продолжение

В начальный момент времени при сильно различающихся проницаемостях слоев (у = 10 2 ) в более проницаемом верхнем слое «локальным» образом возникает многовихревое несимметричное течение (Рис. 9 а , t = 6 - 10 3 год). Но оно достаточно быстро перестраивается в асимметричное двухвихревое и остается таковым на протяжении всего последующего времени моделирования (Рис. 9 а , t = 10 5 год). Наблюдается очень слабое проникновение течения в нижний слой области, о чем свидетельствует слабое искривление изолиний концентрации. В верхней части области, где течение интенсивное, смесь перемешивается и далее остается практически однородной (Рис. 9 б ).

При увеличении проницаемости верхнего слоя, так что у = 10 1 , в нем образуется несимметричное трехвихревое течение, которое на протяжении длительного времени перестраивается к одновихревому (Рис. 9 в ). Диффузия течения в нижний слой незначительна, поэтому установившееся распределение концентрации достаточно близко к линейному по вертикали. Одновихревое течение в верхней части области создает небольшой горизонтальный градиент концентрации примеси (Рис. 9 г , t = 10 5 год).

При близких проницаемостях (у = 5 -10¹), как и в случае плоской границы слоев, в области возникает «крупномаштабное» четырехвихревое течение со смещением его интенсивности в более проницаемый слой (Рис. 9 д ), которое достаточно сильно воздействует на концентрацию (см. на характер изолиний, Рис. 9 е ).

• 4.    Заключение

В работе представлены результаты численного моделирования нелинейных режимов конвекции в прямоугольной пористой области смеси тетралина и додекана, взятых в равных долях. Компоненты смеси являются представителями основных групп углеводородов, встречающихся в нефтяных месторождениях. Область пористой среды ограничена твердыми, непроницаемыми стенками и разделена на два слоя с одинаковой пористостью, но различными параметрами проницаемостями. Отношение проницаемостей слоев может быть как меньше единицы, так и больше нее. Рассмотрены два варианта формы границы слоев. В одном случае слои горизонтальны и имеют равную высоту, в другом — граница имеет вид дуги окружности, обращенной выпуклостью вниз. Последний случай имитирует границу геологической синклинальной складки. Область поддерживается при постоянном нагреве снизу, который соответствует среднему геотермальному градиенту.

При значительно различающихся проницаемостях слоев (проницаемость в одном из слоев в десять или сто раз выше, чем в другом) в области наблюдается «локальное» возникновение и существование конвекции, то есть течение зарождается и развивается в дальнейшем только в слое с большей проницаемостью. С ростом проницаемости второго слоя установившееся течение незначительно проникает в этот слой. При близких значениях проницаемостей слоев образование конвекции носит «крупномасштабный» характер: течение зарождается и существует во всей области, но сдвинуто в слой с большей проницаемостью. Показано, что при близких проницаемостях слоев в области устанавливается одно-, двух- или четырехвихревое стационарное течение. При сильно различающихся проницаемостях слоев характерны сложные по форме квазипериодические или нерегулярные колебания, структура течения в этом случае одно- или двухвихревая.

Распределение концентрации примеси при «локальном» развитии конвекции и значительно различающихся проницаемостях слоев практически однородно в слое, где наблюдается конвекция (слой с большей проницаемостью) и близко к линейному по вертикали распределению в слое, куда течение практически не проникает (слой с меньшей проницаемостью). Уменьшение разности проницаемостей приводит к большему внедрению течения в менее проницаемый слой. В этом случае изолинии концентрации обладают характерной пальцеобразной формой.

При изогнутой границе слоев меняются интенсивность (как в большую, так и в меньшею сторону в зависимости от отношения проницаемостей), структура установившегося течения, степень его диффузии в менее проницаемый слой, распределение концентрации примеси. Влияние того, какой из слоев будет более проницаемым (верхний или нижний), для изогнутой границы оказывается более существенным, чем при плоской границе. Для небольшой разности проницаемостей и плоской границы изменения в интенсивности течения и разделении компонентов смеси не обнаружены (симметрия течения относительно границы слоев при перемене проницаемостей местами). В отличие от этого, при изогнутой границе интенсивность течения и разделение компонентов смеси меняются для любого рассмотренного отношения проницаемостей, так как в более проницаемом слое площадь, на которой возникает течение, другая.

Проведенное моделирование показало очень медленное развитие тепловой конвекции в слоистой пористой среде на временах порядка тысяч лет и формирование установившихся режимов на временах порядка сотен тысяч лет. Образующиеся конвективные течения имеют низкие скорости фильтрации. Однако этих низких скоростей бывает достаточно для перемешивания смеси и предотвращения ее разделения.

При моделировании не были учтены такие факторы, как давление, сейсмическая и тектоническая активности, способные как ускорять, так и замедлять развитие конвекции.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 20-71-00147).