Нелинейные упругие свойства поверхностных тканей тела человека, наблюдаемые методом вдавливания индентора

Для характеризации биологических тканей достаточно широко применяются различные модификации метода вдавливания индентора ( Indentation testing ) [1, 3–16]. Непосредственно измеряемыми величинами являются жесткость, наблюдаемая при фиксированной силе давления или при фиксированной глубине вдавливания [1, 3–9, 11–13, 15, 16], деформационно-нагрузочная характеристика – кривая сила сопротивления – вдавливание [10] либо кривая деформация – время, наблюдаемая при ступенчатом задании фиксированной нагрузки [14]. Подобные измерения используются для оценки упругих свойств тканей в различных условиях и позволяют получить ряд интересных результатов. Так, установлено, что эти свойства являются весьма информативным показателем хода регенерации мышечной ткани после пересадки [4], что они отражают динамику силовых показателей мышц при воздействии на организм человека невесомости [3], развитие утомления мышц [6] и др. Нелинейный характер деформирования биологических тканей индентором существенно усложняет их характеризацию, так как делает невозможным определение единого объективного количественного параметра, определяющего их свойства. Так, например, жесткость, определяемая при фиксированных условиях, оказывается высокочувствительной к выбору этих условий. Задачей данной работы являлось изучение возможностей определения набора объективных характеристик нелинейных упругих свойств биотканей в экспериментах по вдавливанию в них цилиндрического индентора с плоским основанием.

Материалы и методы

Проведены две серии измерений по регистрации силы реакции при вдавливании инденторов разных диаметров ( d = 3; 4; 6 и 8 мм) в ткани бицепса плеча и в ткани тыльной поверхности предплечья в области разгибателя кисти, а также одна серия измерений при вдавливании индентора диаметром d = 3 мм в ткани передней поверхности предплечья в области сгибателя кисти. Все эксперименты проведены на одном испытуемом добровольце. В первых двух сериях экспериментов исследовались эффекты изменения диаметра индентора с целью нахождения нормировки экспериментальных данных, исключающей их зависимость от диаметра. В третьей серии измерений исследовались эффекты изменения состояния тканей. Задавались состояние расслабления ( R ), состояние напряжения ( S ) (вызывалось сжатием кистевого динамометра с силой 50 Н) и состояние отека ( O ) (вызывалось пережатием плеча манжетой для измерения артериального давления с давлением 100–110 мм рт. ст. в течение 1–3 мин). В каждом состоянии проведено семь записей по три вдавливания/отведения индентора диаметром d = 3 мм. Записи в каждом состоянии проводились в отмеченной точке предплечья с интервалом не менее суток. Результаты измерений впоследствии усреднялись.

Во всех экспериментах использован специализированный регистратор деформационно-нагрузочной характеристики, совмещающий в себе тензометрический датчик силы со сменным индентором и индуктивный датчик смещений (рис. 1). Индентор 1 крепится на чувствительном элементе датчика силы 2 , который является достаточно жестким. Вследствие этого его деформации при воздействии реальных сил реакции тканей пренебрежимо малы по сравнению с деформациями тканей. Датчик смещений 3 , представляющий собой подпружиненный стальной сердечник, двигающийся в катушке с переменным током, напротив, является достаточно мягким. Вследствие этого деформации тканей, в которые упирается основание датчика смещений при тестировании тканей, также пренебрежимо малы по сравнению с их

Рис. 1. Регистратор деформационно-нагрузочных характеристик:

1 – индентор; 2 – датчик силы; 3 – датчик смещений

деформациями индентором. Основание датчика смещений сделано площадью около 1 см2 и отстоит от места вдавливания индентора на расстояние 2 см, что исключает смещения точки опоры датчика смещений за счет прогиба поверхности тканей при их деформировании индентором.

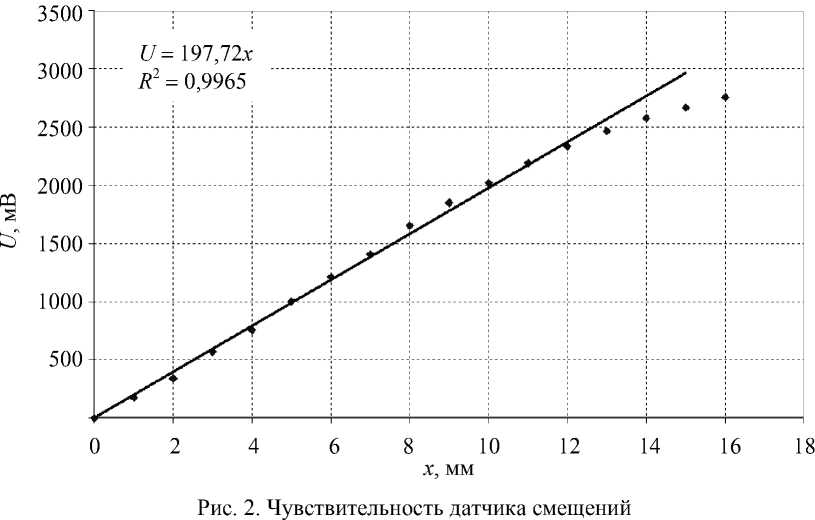
Процедура тестирования тканей состоит в медленном и плавном вдавливании/отведении индентора при удержании датчиков в руке. Основание датчика смещений касается тканей одновременно с индентором. Сигналы датчиков синхронно вводятся в компьютер с тактовой частотой 10 Гц. Датчик силы предварительно калибруется путем установки на него груза известной массы. В результате показания датчика силы ( F ) вводятся в компьютер в граммах силы. Чувствительность датчика смещений проверяется в предварительных экспериментах, когда регистратор деформационно-нагрузочной характеристики закрепляется на штативе с вертикальным лифтом и миллиметровой шкалой, а основание датчика смещений упирается в поверхность стола. Результаты проверки чувствительности датчика смещений приведены на рис. 2. Видно, что датчик смещений можно считать линейным в диапазоне смещений x = 0...12 мм с чувствительностью 197,7 мВ/мм. Таким образом, для определения смещений (мм) по вводимым в компьютер сигналам датчика (мВ) нужно их поделить на 197,7.

На рис. 3 приведен пример зарегистрированных сигналов датчиков в ходе полного цикла вдавливания индентора диаметром d = 3 мм в расслабленный бицепс и соответствующая этим сигналам деформационно-нагрузочная характеристика.

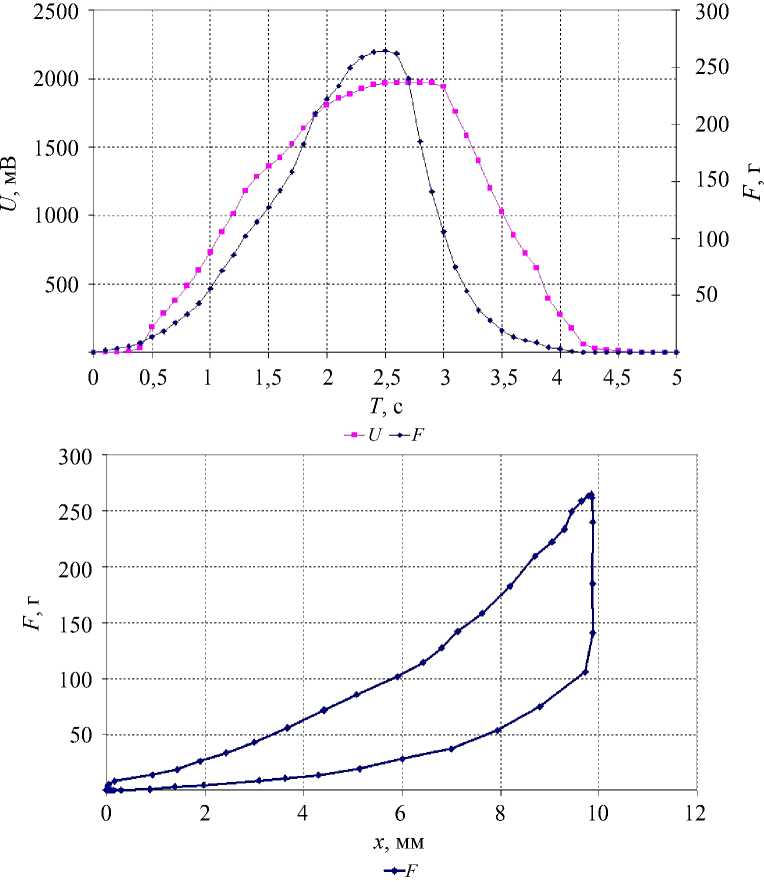
Рис. 3. Сигналы датчиков (вверху) и соответствующая деформационнонагрузочная характеристика (внизу): F – приложенная сила; U – электрическое напряжение, регистрируемое датчиком смещений

Характерной является существенная разница на участках вдавливания и отведения деформационно-нагрузочной характеристики. В ходе экспериментов проводилась регистрация зависимостей такого типа. В ходе обработки проводилась их нормировка, преобразующая к виду номинальное напряжение ( σ ) – номинальная деформация ( ε ), проводилась аппроксимация участков вдавливания и отведения и находилась площадь петли гистерезиса.

Способ преобразования кривых сила – вдавливание в кривые напряжение – деформация основан на известном теоретическом соотношении для вдавливания плоского круглого штампа в линейное изотропное полупространство. Связь глубины вдавливания ( x ) и приложенной силы ( F ) здесь имеет вид [2]

F (1 - ν ² ) dE

где E и ν – модуль Юнга и коэффициент Пуассона.

Поделив левую и правую части этого равенства на площадь основания индентора π d ²/4, считая биоткани несжимаемыми ( ν = 0,5) и вводя обозначения

4 F 16 x

2, 8 = п d23

получим из (1) связь этих величин в виде закона Гука о = E 8.(3)

Соотношения (2) приняты за определения номинального напряжения и номинальной деформации и использованы для нормировки экспериментально измеряемых деформационно-нагрузочных характеристик.

Полученные зависимости о(8) на участке вдавливания аппроксимировались полиномом вида о = E 8 + A82 + B 83,

где коэффициенты Е , А и В имеют смысл, соответственно, линейного и нелинейных модулей упругости.

Интегрированием аналитических выражений для зависимостей номинальное напряжение – номинальная деформация (везде далее в тексте для краткости будут называться просто зависимости напряжение – деформация) на участках вдавливания и отведения вычислялась площадь ( S ) петли гистерезиса. Для корректного сравнения уровня гистерезиса в экспериментах с разными значениями достигнутой максимальной деформаций (8 _max) производилась нормировка площади петли с учетом максимальной деформации. Определяемый таким образом параметр уровня гистерезиса

5 = S /8 max                                          (5)

имеет размерность напряжения и смысл высоты прямоугольника с площадью, равной площади петли гистерезиса S, и длиной 8 _max.

Результаты

На рис. 4 приведены примеры исходных записей сила – вдавливание, регистрируемых с помощью разных инденторов. На рис. 5 приведены расчетные кривые напряжение – деформация для бицепса и предплечья, полученные из исходных записей с помощью нормировки (2). На рис. 6 приведены кривые напряжение – деформация, зарегистрированные в ходе полного цикла вдавливания/отведения индентора с диаметром d = 3 мм на расслабленном и на напряженном бицепсе. На рис. 7 и 8 приведены примеры кривых напряжение – деформация, зарегистрированные в ходе полного цикла вдавливания/отведения индентора с диаметром d = 3 мм на тканях предплечья в области сгибателя кисти в расслабленном состоянии, в напряженном состоянии и в состоянии модельного отека. Уравнения на графиках дают аппроксимации участков кривых, соответствующих прямому и обратному движению индентора. В таблице приведены соответствующие усредненные значения линейных и нелинейных модулей упругости тканей в различных состояниях. Здесь же приведены значения параметра уровня гистерезиса s , найденные по площади петли гистерезиса нормировкой (5).

Параметры сгибателя кисти

Состояние тканей	E , кПа	A , кПа	B , кПа	s , кПа
Расслабление	29,9 ± 2,5	–1,5 ± 0,9	1,1 ± 0,1	73,0 ± 6,0
Напряжение	24,8 ± 6,0	41,4 ± 8,5	–2,2 ± 1,5	96,3 ± 4,5
Отек	35,5 ± 4,1	11,7 ± 2,8	0,5 ± 0,4	69,6 ± 7,3

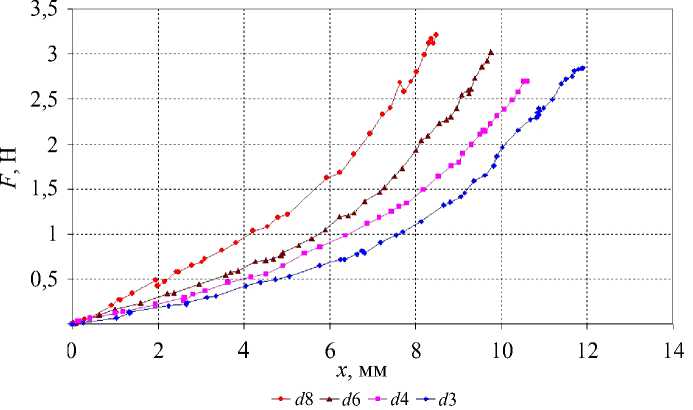
Рис. 4. Зависимости сила – вдавливание, полученные на расслабленном бицепсе в ходе вдавливания инденторов с диаметрами d = 3 мм ( d 3), d = 4 мм ( d 4), d = 6 мм ( d 6) и d = 8 мм ( d 8)

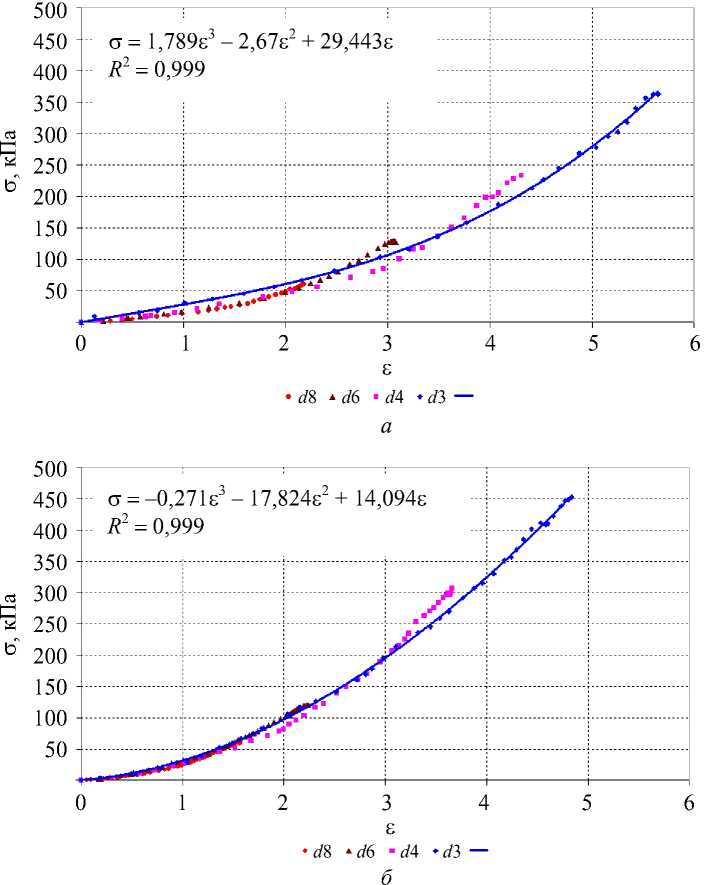
Рис. 5. Кривые напряжение – деформация бицепса ( а ) и разгибателя кисти ( б ), соответствующие вдавливанию разных инденторов

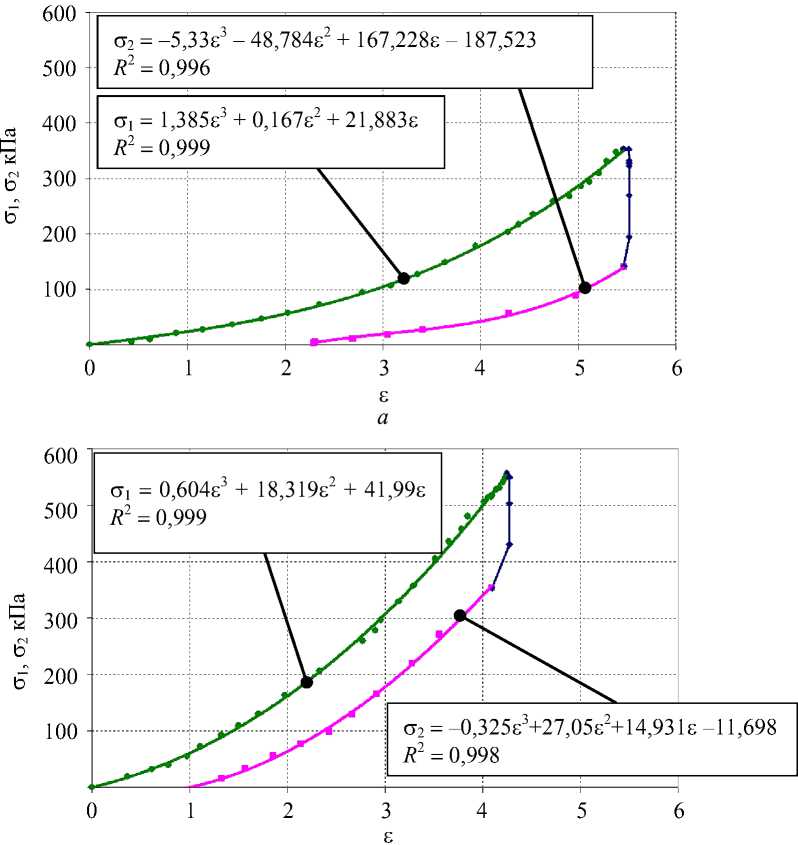
б

Рис. 6. Кривые напряжение – деформация расслабленного ( а ) и напряженного ( б ) бицепса, полученные при вдавливании/отведении индентора d = 3 мм

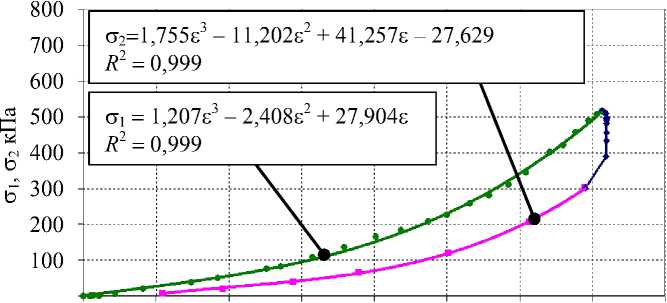
0       1       2      3      4      5       6       7      8

ε

Рис. 7. Кривые напряжение – деформация сгибателя кисти в расслабленном состоянии

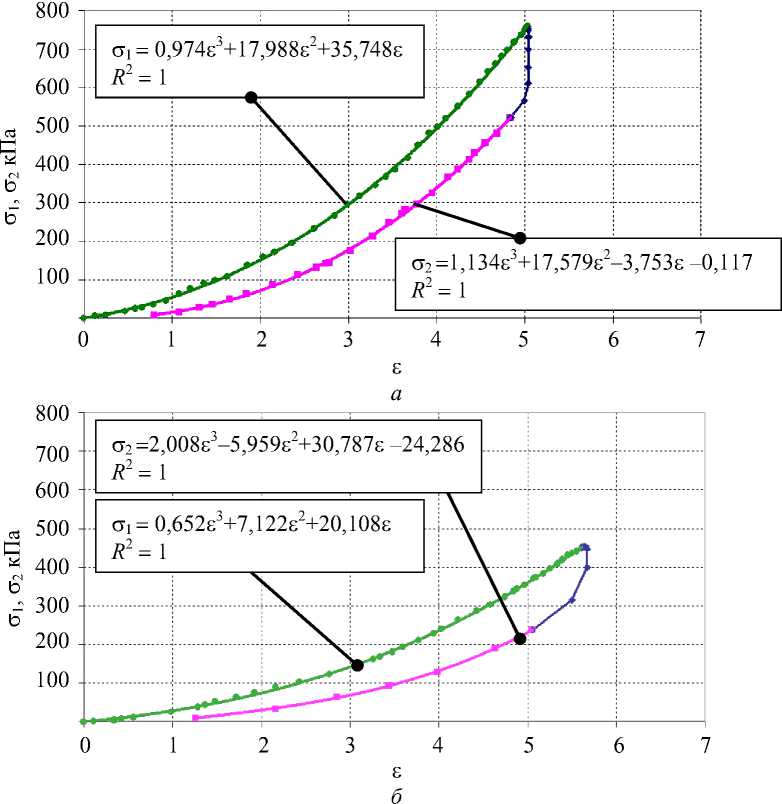
Рис. 8. Кривые напряжение – деформация сгибателя кисти в напряженном состоянии ( а ) и в состоянии модельного отека ( б )

Обсуждение

Регистрируемые кривые сила – вдавливание (см. рис. 4) не могут обеспечить определение объективных характеристик тканей, поскольку существенно зависят от условий эксперимента, в частности от диаметра использованного индентора. В некоторых работах по исследованию биотканей методом вдавливания индентора, например [9, 14], для определения более объективных характеристик используется пересчет кривых сила – вдавливание в кривые номинальное напряжение – номинальная деформация и по их наклону определяются параметры жесткости тканей, совпадающие по размерности с модулем упругости.

Для определения номинального напряжения используется нормировка силы с учетом площади индентора, а для определения номинальной деформации – нормировка вдавливания с учетом толщины слоя исследуемых тканей. В экспериментах автора аналогичный пересчет ничего существенного не дает, поскольку зависимости, соответствующие разным инденторам, остаются различными. Определение номинальной деформации на основе соотношения (2) существенно изменяет картину. На рис. 5 видно, что зависимости σ(ε) , получаемые инденторами с диаметрами d = 4; 6; 8 мм при нормировке (2) группируются вблизи зависимости, полученной с использованием индентора с диаметром d = 3 мм, хотя и не совпадают с ней идеально.

Таким образом, полностью избавиться от зависимости определяемых параметров от диаметра использованного индентора за счет нормировок (2) не удается, но при использовании индентора минимального диаметра должны определяться характеристики, близкие к усредненным по всему набору использованных диаметров. На основе данного наблюдения для характеризации тканей в разных состояниях использован индентор диаметром d = 3 мм.

Сопоставляя уравнения, соответствующие участкам вдавливания индентора на графиках рис. 6 слева и справа, видим, что напряжение бицепса привело к примерно двукратному увеличению линейного модуля упругости и более чем к десятикратному увеличению нелинейного модуля упругости второго порядка. Нелинейный модуль упругости третьего порядка при этом уменьшился немногим более чем в два раза. Данные иллюстрируют высокую чувствительность модулей упругости тканей, особенно нелинейных, к напряжению мышц. Для расслабленного и напряженного бицепса по зависимостям рис. 6 определены значения уровня гистерезиса s = 89,3 кПа и s = 95,4 кПа. Таким образом, при напряжении бицепса отмечается незначительное увеличение уровня гистерезиса. Сходная картина наблюдается по результатам более тщательного исследования параметров тканей в разных состояниях, проведенного на предплечье в области сгибателя кисти (см. рис. 7, 8). Из таблицы видно, что по отношению к расслабленному состоянию при напряжении и при отеке линейные модули упругости тканей E изменяются слабо ( p > 0,4), в то время как нелинейные модули упругости A изменяются достоверно ( p < 0,007). Видно также, что совокупная картина изменений всех параметров при напряжении и при отеке существенно различается.

Любопытно, что параметры уровня гистерезиса s в состоянии расслабления и в состоянии модельного отека оказались близкими ( p > 0,8), в то время как в состоянии напряжения этот параметр достоверно увеличен ( p < 0,05). Причиной гистерезиса, по-видимому, является выдавливание жидкости из области деформирования и существенная инерционность процессов ее обратного притока. Близость и различие параметров гистерезиса могут быть связаны, таким образом, с одинаковыми условиями обратного притока жидкости в ткани в состояниях расслабления и модельного отека, с одной стороны, и с изменениями этих условий при напряжении мышц – с другой.

Заключение

• 1.    В экспериментах по вдавливанию индентора в ткани бицепса и предплечья человека показана возможность преобразования регистрируемых кривых сила – вдавливание в кривые номинальное напряжение – номинальная деформация, слабо зависящие от диаметра использованного индентора.

• 2.    На основе аппроксимации кривых номинальное напряжение – номинальная деформация показана возможность определения набора объективных механических характеристик тканей, имеющих смысл линейных и нелинейных модулей упругости и параметра уровня гистерезиса.

• 3.    Найдены модули упругости и уровни гистерезиса тканей предплечья в расслабленном состоянии, в напряженном состоянии и в состоянии отека. Обнаружена более высокая чувствительность нелинейных модулей к состоянию тканей и показана возможность различения состояний ткани по набору ее модулей упругости.

Благодарности

Работа выполнена при поддержке гранта Правительства РФ № 11.G34.31.0066.