Нелинейный анализ долговременного движения пассивного спутника на солнечно-синхронной орбите и его механического захвата космическим роботом

В [1], [2] исследован аварийный режим (АР) системы управления движением (СУД) информационного спутника на солнечно-синхронной орбите (ССО) с наведением орта к плоскости панелей солнечных батарей (СБ) в направлении Солнца при назначении требуемого углового положения космического аппарата (КА) относительно этого направления с использованием информации о положении орта, ортогонального плоскости эклиптики. При этом устанавливаются устойчивые нелинейные угловые колебания корпуса КА из-за «конфликтующих» воздействий возмущающего гравитационного момента и управляющего момента магнитного привода (МП) на каждом витке ССО. Такой энергосберегающий аварийный режим вполне приемлем при его длительности до нескольких недель. При необходимости долговременного

(несколько месяцев) консервации КА с сохранением возможности восстановления работоспособности его СУД в [3] был предложен и исследован более экономичный АР, где применяется пассивная гравитационная стабилизация спутника при ситуационном включении магнитного привода. На рис. 1 представлены связанная с корпусом КА система координат (ССК) B (O xyz ) с ортами b i и связанная с панелями СБ система координат P , оси которой x ^p , y ^p и z ^p в парковом положении панелей СБ (при γ ^p = 0 ) параллельны соответствующим осям ССК. Орбитальная система координат (ОСК) O (O x ^o y ^o z ^o) с ортами o _i вращается в инерциальном базисе I с вектором угловой скорости Ш _о . Вводятся орт e направления на Землю и орт s направления на Солнце. В отличие от [1, 2], здесь при переходе в АР панели СБ разворачиваются на угол γ ^p = -π /2 , а корпус КА (ССК) устанавливается в ОСК с его разворотом на угол ψ = -π /2 относительно оси O y с ортом b ₂ и наименьшим моментом инерции КА. В результате ось O x с ортом b ₁ и ось O ^p y ^p с ортом n ^p совпадают по направлению с осью O z ^o ОСК и обеспечивается максимальный момент инерции КА по оси O x ССК, противоположной по направлению вектору угловой скорости Ю _о , рис. 1. При поступлении команды на длительную консервацию спутника выполняются следующие этапы: (i) КА переводится в орбитальную ориентацию при цифровом управлении МП; (ii) при достижении требуемой точности стабилизации КА в ОСК контур управления МП временно выключается и спутник переходит в режим пассивной гравитационной стабилизации; (iii) для компенсации накопленных вековых возмущающих моментов, в том числе из-за влияния сил солнечного излучения, выпол-

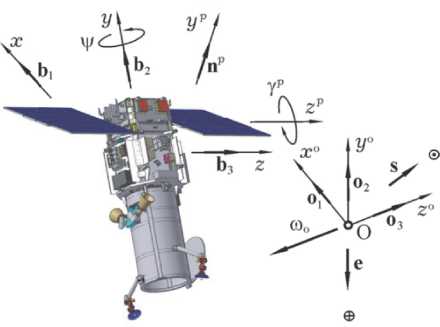
Рис. 1. Схема перехода КА в режим гравитационной стабилизации няется ситуационное кратковременное включение МП, что обеспечивает возвращение КА в орбитальную ориентацию с требуемой точностью.

В [3] выполнен анализ годового перемещения орта s направления на Солнце в ОСК и установлено, что орт s направления на Солнце перемещается в ОСК по образующей поверхности конуса, ось которого направлена по оси O z ^o ОСК, а угол полураствора ф * практически не изменяется в течение каждого витка орбиты. Средние значения этого угла таковы: ф ₅ = 60 град в феврале - сентябре и ф * = 65 град в октябре - январе. В этой работе исследовано движение спутника массой 6500 кг на ССО высотой 720 км, наклонением 98.2695 град и начальной долготой восходящего узла 51 град. Такая орбита прецессирует по долготе восходящего узла со скоростью 0.9889 град/сут, изменение её наклонения носит колебательный характер при наличии малой вековой составляющей. Здесь разработаны законы цифрового управления МП для перевода КА в орбитальную ориентацию, проведен нелинейный анализ длительного (10 суток) движения КА с диагональными элементами тензора инерции 11450, 7150 и 9450 кг м² на указанной ССО и стандартными численными методами установлено, что при гравитационной стабилизации спутника изменение пространственного угла ф y = arccos ( b 2 , o ₂ ) между ортами b ₂ ССК и o ₂ ОСК (местной вертикали) имеет нелинейный колебательный характер с «амплитудой», значение которой в течение месяца может возрасти до 0.8 град.

Для целей данной статьи предполагается, что после приведения отказавшего КА в орбитальную ориентацию с заданной точностью из его конструкции выдвигается спасительный «буй» в виде жесткого стержня для штатного механического захвата космическим роботом-манипулятором (КРМ), рис. 2. Далее бортовая система электропитания спутника полностью отключается и он превращается в пассивный

Рис. 2. Подготовка КРМ к захвату ПКО космический объект (ПКО), перемещающийся в гравитационных полях Земли, Луны и Солнца.

При последующем долговременном (например, годовом) движении ПКО происходит медленное изменение основных параметров ССО – долготы восходящего узла и наклонения. Здесь актуальна задача оценки изменения «амплитуды» нелинейных колебаний ПКО по пространственному углу ф y - необходимо убедиться, что в угловом движении пассивного спутника не возникает режим «кувыркания».

Приводами СУД космического робота-манипулятора являются: (i) двигательная установка (ДУ), которая имеет восемь реактивных двигателей (РД) с широтно-импульсной модуляцией (ШИМ) тяги и позволяет одновременно создавать импульсы векторов тяги и момента произволь -ного направления; (ii) силовой гироскопический кластер (СГК) на основе четырех гиродинов (ГД) – двухстепенных силовых гироскопов . Измерение кинематических параметров движения КРМ выполняется бесплатформенной инерциальной навигационной системой (БИНС), корректируемой сигналами от навигационных спутников GPS/ ГЛОНАСС и звёздных датчиков . Если дальность становится менее 10 м, то эти параметры движения КРМ относительно цели определяются также бортовыми камерами наблюдения и лазерными дальномерами. В работах [4] – [6] рассматривались вопросы навигации, наведения и управления движением КРМ при его сближении с ПКО и механического захвата пассивного спутника в частном случае . В данной статье основное внимание уделяется проблемам нелинейного анализа пространственного механического захвата ПКО.

2.    МАТЕМАТИЧЕСКИЕ МОДЕЛИ

При стандартных обозначениях и отсутствии активных управляющих сил модель движения центра масс КА в инерциальном базисе имеет общеизвестный вид

Г = v; V = -цe r / r3 + ae + am + as, где ae = aen + aea, am и as - векторы ускорения, обусловленные влиянием формы Земли и нерав- номерности распределения её массы, гравитации Луны и Солнца, соответственно. Для моделирования вектора ускорения ae используется разложение гравитационного потенциала Земли в ряд по сферическим функциям до степени n = 8 включительно с применением полиномов Лежандра и коэффициентов зональных гармоник.

В сферической системе координат (вектор r , долгота λ и широта ϕ ) вектор ускорения а _еп зависит от r и ф , а вектор ускорения а _еа зависит также и от долготы λ . Вектор ускорения a _s =Ц ₈( А г /( А т )³ — r s / r^ из-за влияния Солнца определяется его гравитационным параметром g _s и расстоянием от КА до центра Солнца A r = r _s - r , где расстояние r _s от центра Земли до центра Солнца вычисляется по явным аналитическим соотношениям в функции текущей эпохи. Гравитационное влияние Луны моделируется аналогично.

Для описания движения КРМ применяются стандартные обозначения col( - ) = { • } , line( - ) = [ • ] , ( • ) , [a x ] и ° ,~ для векторов, матриц и кватернионов, инерциальная система координат (ИСК) I ; ССК В (О xyz ) КРМ с началом в фиксированном в его корпусе полюсе O (рис. 3) и ОСК O (O x o y o z ⁰) .

Ориентация ССК B в ИСК I определяется кватернионом Л = ( X₀ , X ) , где X = { X i } , вектором параметров Эйлера Л = { X₀, X } , который представляется в форме Л = { С _{ф /2} , e _e S _{ф /2}} с ортом e _e мгновенной оси Эйлера и углом Φ собственного поворота, вектором модифицированных параметров Родрига (МПР) о = { oj = е е tg( Ф /4) , который связан с Λ явными аналитическими соотношениями. Кинематические уравнения для вектора r _o расположения КРМ в ИСК, кватерниона Λ и вектора МПР σ имеют вид

Г _о = r₀ * I M X r ₀ ; Л = Л ° ю/ 2;

; (1)

0 = 4(1 — O2)to + 2 ОХ® + 2 (о,0)0, где вектор ω представляет абсолютную угловую скорость корпуса КРМ в ССК и используется обозначение (•) локальной производной по времени.

Кватернион Л0 ориентации базиса O относительно базиса I определяется уравнением Л0 = Л0 ° ®0/2, а погрешность ориентации базиса B в орбитальном базисе O - кватернионом E = Л0 ° Л = (e0, e), вектором параметров Эйлера E = {Сфe/2, ee Sфe/2} , матрицей Ce = I3 - 2[ex]Q‘e, где Qe = I3e0 + [ex], вектором угловой погрешности 6ф = {6фi} = {2e0ei} и вектором МПР 0е = {ое} = ее tg(Фe / 4). При этом вектор δω погрешности угловой скорости определяется как 5® = ® - Ce®0 (t).

В ССК Oxyz с фиксированным в его корпусе полюсом O положение центра масс C КРМ (робот и манипулятор суммарной массы m = mr + Ami) определяется вектором р c = {x c, y c, z c} по соотношению m рc = L = mrрr + Amiрi. Здесь введен вектор статического момента L , фиксированный в ССК вектор р r представляет положение центра масс Or собственно робота, векторы рi, i = 1 ^ 3 определяют положения центров масс ci (см. рис. 3) трех звеньев манипулятора с массами mi и собственными тензорами инерции Jc.

При моделировании движения КРМ применяется векторная форма классических уравнений Эйлера-Лагранжа [7]. При векторе vo скорости полюса O поступательное движение центра инерции C системы твердых тел КРМ в ССК описывается векторным уравнением mv0 + [-Lx]® = -m ®xv0) + ®x(Lx®)

-A/(m/(2®xр/+р/) + Pe + Fg , где р* =As(дрi 1dqs)qs);

р 7 = ^A s ^{( д} р i / ^d q_s ) q s ^+A k ^{( d 2} р i / ^d < k ^d q_s ) , векторы P ^e и F ^gr представляют силы тяги двигательной установки, центрированной в полюсе O , и гравитации.

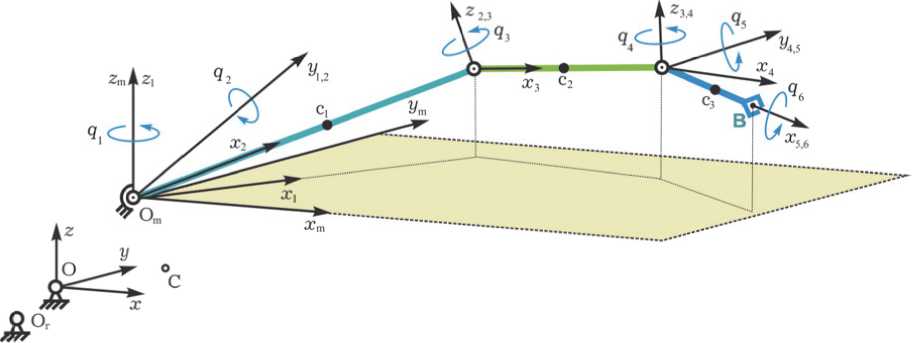
Рис. 3. Кин е матическа я схема космического р обота-ман и пулятора

Введем постоянные тензоры инерции робота J ° в полюсе O и звеньев манипулятора JС в их центрах масс ci. Тензор инерции J механической системы в полюсе O вычисля ется по соотношению J = | Jj | = J° +2Ji, где J i = J° + mi (E PtPi — PiPt) и E является единичным тензором. Через юi обозначим вектор угловой скорости i -го звена манипулятора в ССК. Производная этого вектора по времени имеет вид юi = ю* + ю х юi.

В ССК Oxyz с полюсом O вращательное движение системы твердых тел описывается векторным уравнением

[ L x ] v * + Je b = - L х ( w x v _o)            (3)

-wx (J®+H) - Q - H’ + Me + Mgr, где

Q = E i ( J i ю i + ю x J i ю i + ю i x J i ( ю + ю i )

7        7            X .                   .    **X

⁺ m i -P i -^{x ( ю x ( ю x} P i ) ⁺ 2 ^{ю х} P i ⁺ P i ) .

векторы — H * = M ^g и M ^e = M представляют управляющие моменты СГК с вектором кинетического момента (КМ) H и двигательной установки на основе 8 реактивных двигателей, а вектор M ^gr – гравитационный момент.

Конфигурация манипулятора в ССК определяется столбцом q = { q s } , который составлен из угловых координат q s , s = 1 ^ 6 его трех звеньев, см. рис. 3. Положения P i центров масс звеньев, их линейные P i и угловые to _; скорости, а также ускорения P i и ю i , являются функциями угловых координат q_s и их производных по времени.

Векторные уравнения Эйлера (2), (3) дополняются стандартными уравнениями Лагранжа по степеням подвижности qs манипулятора с обобщенными силами Qs в правых частях. Для целей данного исследования угловые координаты qs в (2) и (4) считаются непрерывным функциями qs (t), заданными на интервале m >ш времени t e [tf , tf J при краевых условиях начального (initial) qi = q(tm ) и конечного (final) qf = q( tm) положений звеньев манипулятора в процессе развертывании его механической цепи.

В исходном фиксированном положении манипулятора q i = q _o = { n , 0, —n , 0,0,0} КРМ является единым твердым телом, полюс O совпадает с его центром масс и вектор статического момента L = 0 . Математическая модель динамики КРМ при таком положении манипулятора следует из (2), (3) и представляется в виде

m( v ‘ + w x v _r ) = P ^e + F ^gr;

J w + w x G = M ^g + M ^e+ M ^gr,

где вектор v r = v o (нижний индекс r, robot) скорости его поступательного движения и век- тор G = Jю + H. Расположение КРМ определяется вектором rr = ro и уравнением r* + ю х rr = vr. Векторы rt и vt (нижний индекс t, target) представляют положение ПКО и скорость его поступательного движения. Модель движения ПКО имеет аналогичный вид, но при отсутствии управляющих сил и моментов (Pe = Mg = Me = 0) и значении H = 0. Векторы дальности до цели Ar = {Ari} и рассогласования между скоростями Av = {Avi} ПКО и КРМ вычисляются по соотношениям Ar = rt — rr и Av = v t — v r .

На рис. 4 приведена схема ДУ на основе 8 РД. Положение ортов ep, p = 1 ^ 8 осей сопел РД в ССК определяется углами ae и pe , векторы P p, p = 1 х 8 точек Op приложения вектора тяги РД в ССК определяются параметрами bx , by и bz . Каждый РД имеет ШИМ тяги, что Vt e[tr, tr+1) описывается нелинейными соотношениями pp (t) = PmPWM( t —TU tr ,Tm ,N pr )

с периодом Te и запаздыванием T,e . Здесь v „ u                                  zu                p является входным сигналом и функции

' slgnv pr 0

PWM( t,t_r, T m ,v pr ) =

t E ^[ ^ + Г pr )

t ^{E [} t r ^{+ T} pr , t r + 1 ) ;

T (t )=< pr m

[ sat( T „ ^e,|v pr |)

Iv pr ¹ ^ ^T m ^|v pr | > ^T m

t_r = rT U , t r + 1 = t r + T U ; r E N = [0,1,2,3...) , Pm

– номинальное значение тяги, одинаковое для РД. Вектор тяги p -го РД вычисляется по формуле p _p ( t ) = — p_p ( t ) e _p , а векторы силы P ^e и момента M ^e ДУ - как P ^e = E p p ( t ) = P = { P 1 , P 2 , P 3 } и M ^e = E [ P p x J p p ( t ) .

Для управления ориентацией КРМ применяется СГК на основе четырех ГД по схеме 2-SPE с ортами векторов кинетических моментов (КМ) h _p ( в _p ) , p = 1 ^ 4 , рис. 5, где приведена также огибающая области вариации нормированного

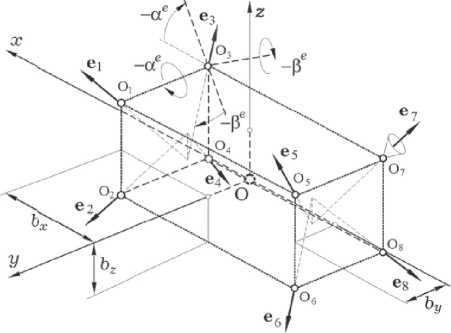
Рис. 4. Схема ДУ на основе 8 РД

вектора КМ h ( P ) = E h p ( P p ) кластера со столбцом p = (P } , и ее проекции на плоскости базиса O x_c’ y _cg z_t’ . c c c

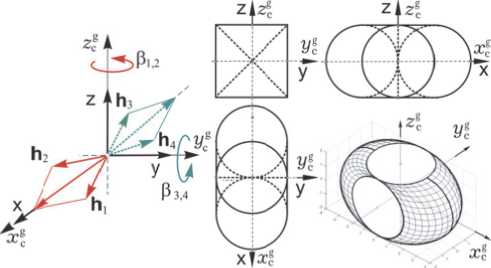
Рис. 5. Схема СГК и обл а сть вариац и и его КМ

Применяемый явный аналитический закон настройки СГК (распределения трехмерного вектора его управляющего момента М ^g = {М g } между четырьмя ГД) позволяет исключить избыточность данного кластера с вектором кинетического момента H = h _c h ( P ) , где h _c - одинаковое для всех четырех ГД постоянное значение модуля собственного КМ.

При цифровом управлении u k ( t ) = {u ^g _k ( t )} с периодом T u , где ^{u g} _k ⁽ t ⁾ = ^{u g} _k ^V t G ^[ t_k ^, t_{k + 1} ⁾, t_k + 1 = t k + T_u и k g N₀ , СГК формирует вектор управляющего момента ■

M k ( t ) = - h c A h ( P ( t ) u C (t ) ; P C t ) = u k ( t ) , (5) где матрица Якоби A _h ( p ) = 5 h ( P ) d p .

Применяемый закон цифрового управления МП при переводе спутника в аварийный режим гравитационной стабилизации описан в [3], а законы широтно-импульсного управления ДУ и цифрового управления СГК в системе управления движением КРМ подробно представлены в [6].

3.    СТРАТЕГИЯ УПРАВЛЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Встреча КРМ с ПКО начинается при дальности до цели A r = | A r | = 500 м в условиях видимости цели видео системой КРМ. Для значений A r g [500,10] м закон наведения КРМ синтезируется в виде набора гладко сопряженных векторных сплайнов как векторных функций МПР о ( t ) при заданных граничных условиях пространственного перемещения КРМ за назначенное время. При этом используется прогноз орбитального расположения ПКО в назначенное время и учитываются допустимые изменения ускорений поступательного перемещения КРМ. Этот закон наведения реализуется ДУ и СГК по отфильтрованным сигналам БИНС на интервале времени t g [0,500] с.

При дальности менее 10 м на сегментах орбиты, освещенных Солнцем, выполняется идентификация кинематических параметров пространственного движения ПКО на основе информации от наблюдательных средств КРМ. С применением сигналов этих средств заданная дальность обеспечивается ДУ совместно с СГК в режиме слежения за ПКО с точностью 0.1 м на интервале времени t g [500,700] с и далее вплоть до момента времени tz , когда происходит сцепление КРМ с ПКО.

Этап подготовки КРМ к захвату ПКО содержит три стадии: (i) развертывание манипулятора на интервале времени t g [ t i ^m , t fm ] = [700,900] с из начального положения q i в заданное q _f , которому соответствует положение B _f на рис. 6 точки B схвата (рис. 3) манипулятора; (ii) «зависание» КРМ над подвижным ПКО на интервале времени t g [900,980] с, где по сигналам наблюдательных средств КРМ уточняется фактическое положение точки B относительно точки A спасательного «буя» ПКО; (iii) изменение вектора состояния q ( t ) манипулятора на интервале времени t g [980,1080] с в режиме слежения за перемещением точки B схвата из положения B _f в положение B z , когда q ( t z ) = q z в момент времени t z = 1080 с. Завершающий этап захвата пассивного спутника состоит в механическом сцеплении точки A «буя» и точки B схвата, см. рис. 6, где указаны отсчетная точка D ПКО и размерные параметры в метрах.

Для анализа динамики пространственного сцепления КРМ с ПКО вводятся шесть дополнительных координат, составляющих векторы q ^ = { 5ф £ i } проворачивания и q d = { 5 5 b i } поступательного проскальзывания точки A «буя» в схвате манипулятора, а также векторы скоростей ю ^ = { 5ю ^ i } и v b = { 5 v b i } этих перемещений в системе координат схвата. Соответствующие обобщенные силы принимаются в виде сил и крутящих моментов сухого трения

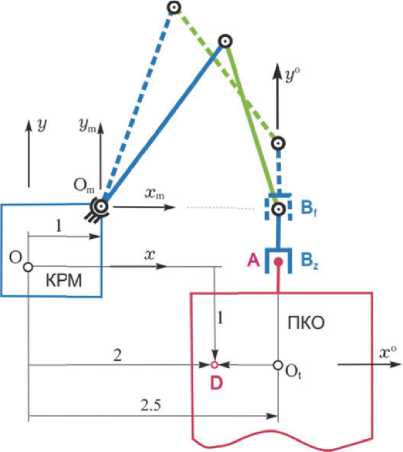
Рис. 6. Схема захвата ПКО

Q'   M;,=-M;"sign(8«t,), е> rf =- pb-sign(8v;,),/ = i+з, Mfm fm b и rb имеют заданные постоянные значения.

Ставятся следующие задачи: (i) нелинейный анализ изменения «амплитуды» нелинейных колебаний при годовом движении ПКО на указанной солнечно-синхронной орбите; (ii) анализ точности стабилизации достигнутого положения КРМ при развертывании манипулятора в заданное положение и подготовке его к захвату подвижного ПКО; (iii) нелинейный анализ динамики пространственного сцепления точки B схвата КРМ с пассивным спутником в концевой точке A его спасательного «буя» в момент времени t z = 1080 с; (iv) нелинейный анализ движения образованной жесткой связки двух космических объектов при ее гиросиловой стабилизации в орбитальной системе координат.

4.    АНАЛИЗ ГОДОВОГО ДВИЖЕНИЯ ПАССИВНОГО СПУТНИКА

Исследовано угловое движение КА на ССО высотой 720 км, когда спутник с указанными выше параметрами с помощью МП приводится в орбитальную ориентацию. Компьютерная имитация выполнена при переходе КА из ориентации в подвижной солнечно-эклиптической системы координат [1, 2] при значении угла фе = 11 град в орбитальную ориентацию. На рис. 7 в двух масштабах приведены изменения пространственного угла φy при таком переходе в течение 2.986 суток (четырех витков орбитального полёта), где красной точкой отмечен момент времени отключения бортового электропитания КА и его превращения в ПКО. На рис. 8 представлены изменения угла φy начиная с номера витка n = 5 до 145 витка полёта ПКО включительно, т.е. в течение 10 суток [3].

Гравитационные возмущения от Луны и Солнца приводят к модуляции «амплитуды» нелинейных угловых колебаний КА относительно местной вертикали с месячным и годовым периодами. На рис. 9 представлены изменения угла φ _y на годовом интервале времени от 01.01.2018 в 00:00:00 до 31.12.2018 в 24:00:00. Здесь нетрудно убедиться, что максимальные значения угла φ _y достигают 0.74 град с периодом 117 дней. При анализе долговременного движения ПКО на ССО необходимо также учитывать влияние сил давления солнечного излучения, где требуется конкретная информация о форме, размерах и отражательных свойств конструкции пассивного спутника.

5.    АНАЛИЗ УПРАВЛЕНИЯ КРМПРИ ПОДГОТОВКЕ К ЗАХВАТУ ПКО

Пусть расположение отсчетной точки D ПКО в ССК робота определяется вектором rD = {2, -1, 0} м, см. рис. 6. Тогда при стабилизации заданного положения КРМ относительно ПКО сначала на интервале времени t е [700,900] с выполняется развертывание манипулятора из исходного положения qi в заданное положение qf = {66.33,- 0.32,-128.66,- 27.66,- 0.25,10} град,

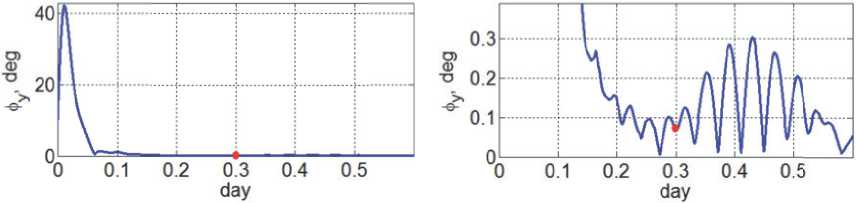
Рис. 7. Изменение простра н ственного угла ф y пр и переходе с путника в о рбитальну ю ориентацию

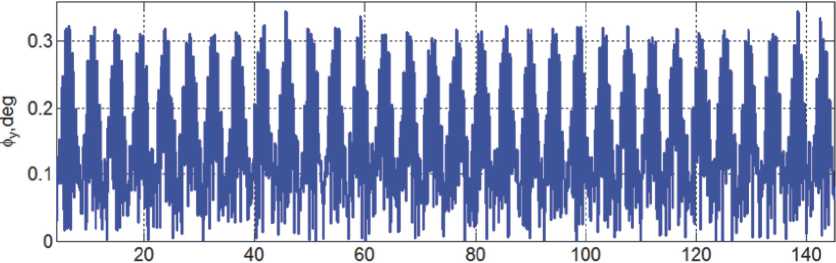
п

Рис. 8. Пространственн ы й угол ф y о риентац и и орта Ь ₂ о тносител ь но местн о й вертикали

0.8

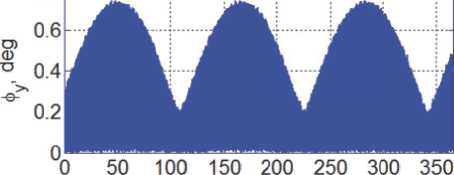
day

Рис. 9. Изменение угл а ф y в тече н ие года

готовке к захвату ПКО. Происходящие при этом изменения тензора инерции и координат центра масс КРМ приведены на рис. 12 и 13. Вариации вектора скорости поступательного перемещения точки B на рис. 14, изменения вектора тяги ДУ при подготовке робота к захвату ПКО на рис. 15, а также ошибки угловой стабилизации КРМ и вариации вектора стабилизирующего момента СГК на рис. 16 и 17 соответственно, демонстрируют важное влияние изменений инерционных параметров КРМ при развертывании манипулятора.

которому соответствует вектор гв = {2.5, 0.45,0} м положения Bf точки B схвата. После завершения стадии «зависания» далее на интервале времени t е [980,1080] с вектор состояния q(t) манипулятора изменяется в режиме слежения за перемещением точки B схвата из положения Bf в положение Bz , когда qz = q(tz) = {48.25, 0, -131.89, - 6.35,0,10} град и вектор rB = {2.5, 0, 0} м при t = tz = 1080 с.

На рис. 10 и 11 представлены изменения координат точки отсчета D ПКО в ССК робота и отклонения точки B схвата от его положения B _z при развертывании манипулятора и под-

6.    АНАЛИЗ ДИНАМИКИ ЗАХВАТА ПАССИВНОГО СПУТНИКА

В момент времени t z = 1080 с двигательная установка выключается. При параметрах сил p f™ = 20 Н и моментов М ^” = 30 Нм сухого трения в схвате робота получается весьма бы-стропротекающий динамический процесс сцепления точки B схвата с концевой точкой A спасательного «буя» ПКО. Здесь удобно использовать локальное время т = t - t_z .

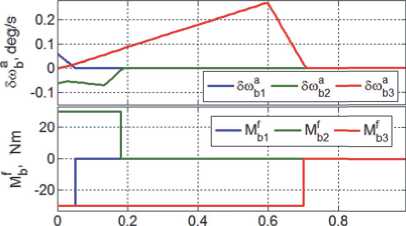
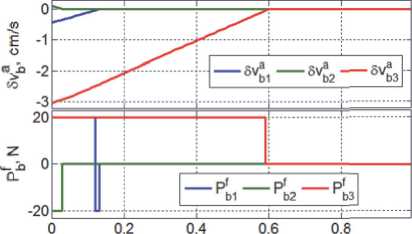
На рис. 18 - 20 представлены соответственно угловые скорости и моменты сухого трения, линейные скорости и силы сухого трения, а также поступательные и угловые перемещения «буя» в

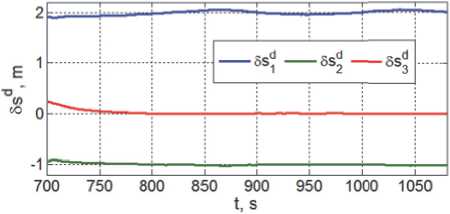
Рис. 10. Вариации координа т точки D в С СК КРМ

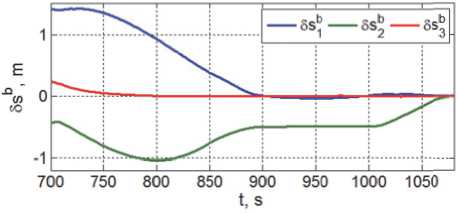
Рис. 11. О тклонения т очки В от п о ложения B_z

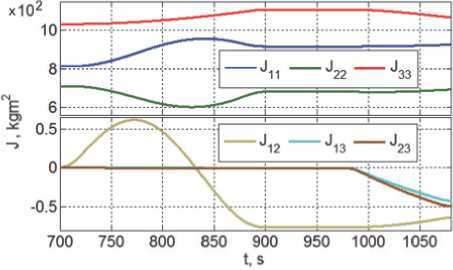
Рис. 12. Изменение тенз о ра инерции КРМ

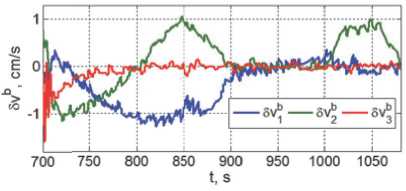
Рис. 14. Вариации в е ктора скоро с ти точки В

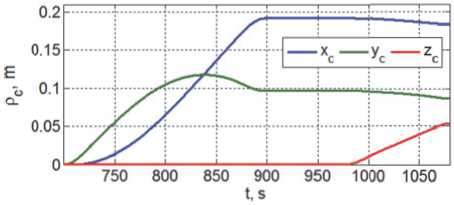
Рис. 13. Изменение коорди н ат центра м а сс КРМ

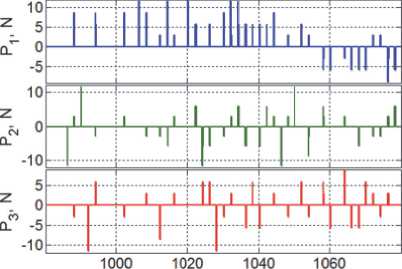
t, S

Рис. 15. В е ктор тяги Д У при подго т овке к захвату

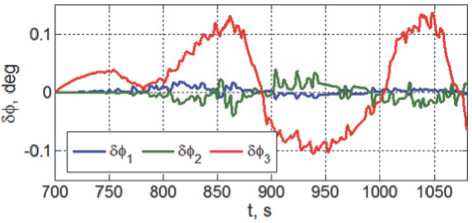
Рис. 16. Ошибки угловой ста б илизации КР М в ОСК

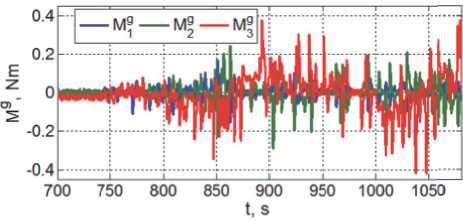
Рис. 17. Стабилиз и рующий м о мент СГК

схвате робота. Длительность сцепления по всем шести координатам не превышает 0.75 с, причем здесь продолжительность поворота «буя» в схвате немного превышает длительность его поступательного проскальзывания. На рис. 21 приведены скорости поступательного перемещения полюса КРМ в ОСК в процессе сцепления КРМ с ПКО.

7.    АНАЛИЗ ДВИЖЕНИЯ СВЯЗКИ КРМ И ПАССИВНОГО СПУТНИКА

На рис. 22 - 25 представлены результаты нелинейного анализа углового движения образованной при те [0.1] с жесткой связки КРМ массой 1000 кг и ПКО массой 6500 кг при

г ,8

Рис. 18. Скорости и мом е нты сухого трения

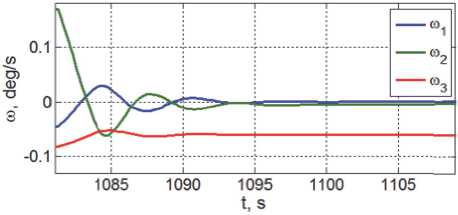
Рис. 22. У гловые ско р ости связ к и КРМ и ПКО

Т,8

Рис. 19. Скорости и си л ы сухого т р ения

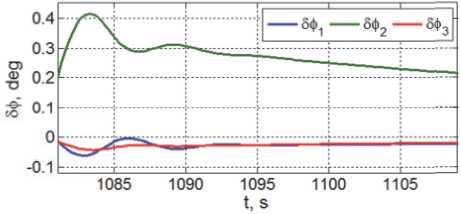
Рис. 23. Углы ори е нтации св я зки в ОСК

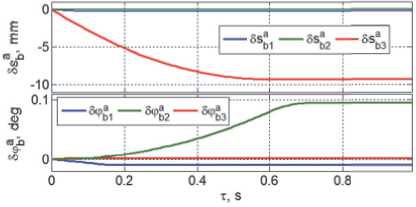
Рис. 20. Линейные и угловы е перемеще н ия «буя»

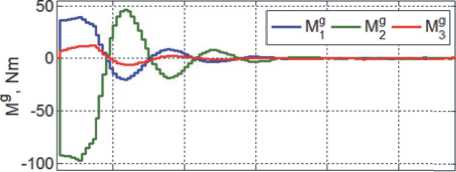
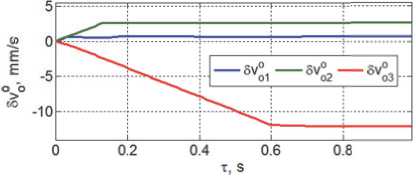
Рис. 21. Скорости по л юса КРМ в О СК

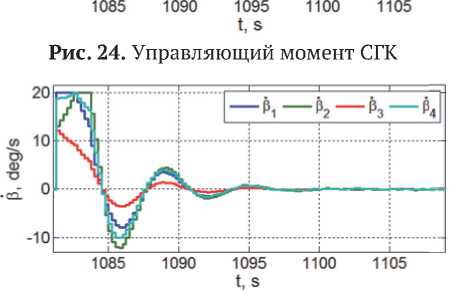
Рис. 25. Угловые скорости г и родинов

последующей ее силовой гироскопической стабилизации в ОСК на интервале времени t е [1080.1, 1110] с.

Последствия косого ударного сцепления КРМ с массивным спутником в отношении абсолютных угловых скоростей и углов ориентации связки двух космических объектов в ОСК демонстрируются на рис. 22 и 23. Здесь очевидно, что влияние ударного сцепления наиболее проявилось по каналу рыскания КРМ, см. графики зеленого цвета.

Изменения управляющего момента СГК и угловых скоростей четырех ГД с модулем собственного КМ h g = 250 Н м с и периодом цифрового управления T u = 0,25 с представлены на рис. 24 и 25. Из сравнения рис. 17 и рис. 24 нетрудно установить, что требования к ресурсу СГК по модулю вектора управляющего момента в произвольном направлении диктуются условиями ударного сцепления КРМ с пассивным спутником.

ЗАКЛЮЧЕНИЕ

Выполнен нелинейный анализ нелинейных угловых колебаний пассивного спутника при его годовом движении на солнечно-синхронной орбите. Проведе н анализ точности стабилизации КРМ при развертывании манипулятора и подготовке его к захвату пассивного космического объекта. Исследована динамика пространственного сцепления КРМ с пассивным спутником, проведен нелинейный анализ движения образованной жесткой связки двух космических объектов при ее силовой гироскопической стабилизации в орбитальной системе координат.

Приведены результаты имитации, демонстрирующие эффективность разработанных алгоритмов управления космическим роботом-манипулятором.