Нелокальная электродинамика сверх- проводника второго рода

Е(г) = (е(г)) = -^ |JJe(r + r')/r', В(г)= (b(r)) = 1 ]Jjb(r+ С^^                 (3)

Соотношение (1) является материальным уравнением среды. Зависимость полного тока от переменного магнитного поля в нем учитывается с помощью третьего уравне-/ ния (2) как в(г)=-с p-ozE^'^' + Bfo). Постоянное магнитное поле Во = В(0) обычно вводится в обобщенную восприимчивость как параметр.

Граничные условия для векторов Е, В и D получаются из уравнений (2) обычным образом [5]:

^> — E_h, В_2п - B_ln, D₂„ — D_ki, S_2t — В^ — 4л//с,      (4)

где i_v — линейная плотность индуцированного в среде полного поверхностного тока, включая ток намагниченности и поляризации.

В сверхпроводнике второго рода в диапазоне радиочастот поляризацией можно пренебречь, разделить же токи намагниченности и проводимости невозможно даже на постоянном токе, т. к. они создаются движением общего конденсата куперовских пар. Поэтому описывать электромагнитные процессы в сверхпроводнике даже на низких частотах следует с помощью обобщенной индукции.

Материальное уравнение сверхпроводника

Уравнения Гинзбурга — Ландау [Г] получены минимизацией свободной энергии, они и следующее из них уравнение абрикосовского вихря [2] описывают стационарное термодинамически равновесное состояние. Нестационарные процессы, сопровождающиеся диссипативным движением вихрей, целесообразно описывать методами формализма Лагранжа. Построим нерелятивистский лагранжиан сверхпроводящего конденсата, описываемого волновой функцией (параметром порядка) ц/, исходя из известной функции Лагранжа классической заряженной частицы в магнитном поле L = mv²/2 + evA/c - U [5].

По аналогии с построением свободной энергии сверхпроводника [1] представим оператор скорости v как — (ih/2m)N - (е/стУХ, добавим слагаемые, учитывающие квантовый характер сверхпроводящей компоненты [1; 6], и лагранжиан электромагнитного

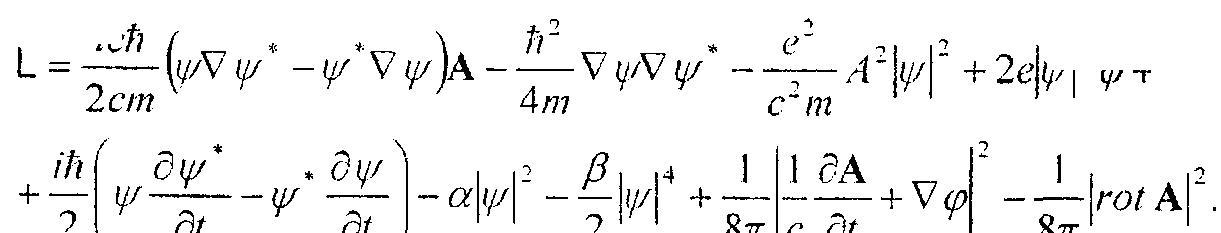
поля [7]. /ед ,     ,         \ 1г         . е2 L = —— ly/Viz/ -ш ViylA--V i//V ш -----A 2cm               4m        c~m ih( dp* . dp\ । ,2 7 |4   1 1 SA 2 Г dt       dt J          2 8к c dt

2Ы" + 2еЫ"р + (5) 2        1                7 + Vc2--|ro/A‘.

Здесь использовано выражение [4] для потенциальной энергии переменного заряда в заданном потенциале и учтено, что е = - (1/с)дА/дГ - Уф.                               (6)

Уравнение Лагранжа для непрерывной среды имеет вид [6]:

dL  д si     a st     а аь     a at = эр cq,  St S^dqjdt)  SxS^SqJSix)  Sy S{SqJSy)  3z5^dqJB^  d(<3q,/3ty          ^^

Здесь роль обобщенных координат выполняют полевые функции g/r, t), для лагранжиана (5) это параметр порядка у или у* и компоненты вектор-потенциала А_х, А , А?

В правой части уравнения (7) записана производная диссипативной функции по соответствующей обобщенной скорости [8], поскольку сверхпроводящая компонента и электромагнитное поле не образуют замкнутой системы. Ее взаимодействие с кристаллической решеткой и нормальной компонентой приводит к диссипации энергии электромагнитного поля в коре движущихся вихрей. Удвоенное значение диссипативной функции описывает скорость уменьшения энергии в системе. Поскольку диссипация связана с нормальной компонентой, подчиняющейся закону Ома, можно положить F= |ера_я/2, где с_п — проводимость нормальной компоненты, пропорциональная концентрации неспаренных электронов.

Вычисляя соответствующие производные лагранжиана (5) и диссипативной функции, подставляя их в уравнения (7), после несложных векторных преобразований с учетом соотношения (6) получим

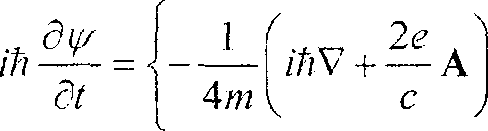
л-2еф-а -р\у\" у/

, 8ле2 । |2 . i2Tteh / „ ,           \ 4гт 1 де rot rot А =--— Ы А +-----ly/V у/ - у/ V у/1+ —■ сг,е +--.

ст       ст                с с St

Здесь А - микроскопический (неусредненный) вектор-потенциал. Уравнение (8) можно рассматривать как уравнение Шредингера, выражение в фигурных скобках представляет собой гамильтониан системы.

В стационарном случае, когда производные по времени равны нулю, интегрирование уравнений (8), (9) [9] совместно с уравнением Максвелла div е = 8пе(|ц/|² - |у₀|²), где у/₀ = -^-а)р = фк/- ~ параметр порядка без поля, показывает, что параметр порядка и потенциал вблизи границы сверхпроводника с вакуумом меняются на расстоянии порядка длины когерентности ^. Это значит, что в глубине сверхпроводника электрическое поле отсутствует, и постоянное значение потенциала можно положить равным нулю. Тогда стационарные уравнения (8) и (9) совпадают соответственно с первым и вторым уравнениями Гинзбурга — Ландау [1].

Учитывая, что в силу уравнения Максвелла

. 4тг . 4тг        1 де

(Ю)

(И)

rot rot А =—j s + — с„е +-- с с       с dt уравнение (9) можно записать в виде

2е । >2 , ieti / „ .            \

Г =—и а+—^у/ "У у^т ст 2т который справедлив и в нестационарном случае. Это естественно, поскольку оно совпадает с квантовым средним тока сверхпроводящей компоненты.

Пусть Т(г, t) = ф(г, О/у_о⁼ W ехр(Ю). Тогда уравнение (11) принимает вид

4лй2

f— vs-a!

V2e )

где ^ ""Ч^-у^Г ~ глубина проникновения. Мнимая часть уравнения (8) при этом с учетом соотношения (12) принимает вид уравнения непрерывности сверхпроводящей компоненты

■

——-=--divj„ , ct ens а действительная часть соответственно

30   ti f2с  Т   at i2 ) 2е

St    4т   |^| cti     j   ti "            h'

Если вне кора положить |Т| = 1, а радиус кора вихря в не слишком сильном поле считать пренебрежимо малым, то, взяв ротор от уравнения (12), с учетом формул (2) и (10) получаем [9]

, 4лсгаь л2 а:ь _ „/\

Ь + Л~ rotTOtb + —--;--+—;--г = фдг-г,).

С' St С' дг

Здесь r_z — координаты центра вихря, Ф_о = Ф_о1₍, где l_z — единичный вектор, направленный вдоль оси вихря, Ф_о = Tlicje — квант магнитного потока.

В стационарном случае уравнение (14) совпадает с известным уравнением неподвижного абрикосовского вихря [9]. Для вихря, движущегося со скоростью v вдоль оси х, четвертое слагаемое в правой части уравнения (14) равно (X²v²/c²)5²b/5x² и описывает деформацию движущегося вихря, связанную с лоренцевым сжатием. При v << сим можно пренебречь и считать, что движущийся вихрь не деформирован. Третье слагаемое связано с током нормальной проводимости. Так как этот ток не взаимодействует со сверхпроводящей компонентой, оно не искажает и распределения сверхпроводящего тока, и параметра порядка относительно кора движущегося вихря.

Усредним уравнение (14) по объему V, содержащему много параллельных вихрей, выбрав его в виде цилиндра с основанием S, перпендикулярным оси вихрей, и образующей, параллельной осям вихрей:

„         „ 4^(7,, ав л2 а2в

B+Л rotrot^A --;---+ ——— = лФ₀                 (15)

с² dt с- dt^{2                                  v 7}

где п — концентрация вихрей. При усреднении принято, что формула (5), вытекающая из теории Гинзбурга — Ландау [1], применима при малых значениях параметра порядка. Тогда можно считать, что при сверхпроводящем переходе концентрация нормальной фазы меняется незначительно, и нормальная проводимость s_n почти постоянна во всем объеме сверхпроводника.

Из уравнения (15) следует, что только в однородном постоянном поле можно считать В = иФ₀. Это связано с тем, что при усреднении по формуле (3) граница основания S делит некоторые вихри на части, и при неоднородном распределении вихрей они не компенсируют друг друга.

Волновое уравнение (15) можно рассматривать как нелокальное материальное уравнение для смешанного состояния сверхпроводника второго рода. Вместо напряженности магнитного поля Н полевой функцией в нем является концентрация вихрей и. Для того чтобы по заданной концентрации вихрей найти магнитное поле в сверхпроводнике, т. е. решить уравнение (15), необходимо задать на границе значение поля и его нормальной производной.

Как следует из уравнений (4), первое граничное условие определяется плотностью полного поверхностного тока, который зависит от положения вихрей вблизи границы. Второе условие также связано с распределением вихрей в приграничной области. Таким образом, возникает задача дополнительных граничных условий (ДГУ), которые накладываются на функцию и(г). Как и в случае спиновых волн [10], ДГУ, в отличие от электродинамических условий (4), определяются взаимодействием магнитных моментов, в данном случае вихрей, с границей [11]. ДГУ часто возникают в электродинамике нелокальных сред, разработаны эффективные методы их получения и анализа [12].

Динамика вихрей

Как видно из уравнения (15), магнитное поле в сверхпроводнике второго рода определяется динамикой вихрей. Движение вихрей определяет и электрическое поле. Поэтому анализ электродинамики такого сверхпроводника целесообразно проводить кинетическим методом [13].

Рассмотрим движущийся в сверхпроводнике одиночный вихрь. Продифференцируем по времени уравнение (12) с учетом уравнения (13):

+            —а) + У/.

St 4лХ~ %лЛ"е St \ Ис )

Здесь обозначено ~ ^т I |^| 70 сй А .

Первое слагаемое в уравнении (16) совпадает с первым уравнением Лондонов [9] с той разницей, что электрическому полю пропорциональна частная производная плотности сверхпроводящего тока по времени. Второе и третье слагаемые — вклад движущихся вихрей, для неподвижного вихря они равны нулю. При у « с можно считать, что вихрь при движении не деформируется. Поэтому модуль и фаза параметра порядка, плотность сверхпроводящего тока и, следовательно, вектор-потенциал распределены относительно центра тД) движущегося вихря так же, как и в неподвижном.

Обозначим р = г — г_г Тогда 3|ty|²/d/ = v V|y|², где v(r_z) = dxjdt — скорость центра вихря, V9 = 1 х р/р², А = 1 х рЛ(р)/р, V|\|/p = (<5|\y|²/Jp)p/p, V/^-= (df/dp)ptp. Усредним уравнение (16) по физически малому объему, содержащему много вихрей, центры которых г₍. распределены в сверхпроводнике с плотностью п. Нетрудно видеть, что третье слагаемое в силу симметрии вихря при усреднении дает нуль. Тогда

/б],(г)\     с²       he²     гг / у / ч С d\y\ ( 1 2е ) ,

• —= тЕ +--г-1 х mr-cXvlr- с)с ————--- A \d'p

\ ot / 4^3"    8яЛ'е                       р" dp \р tic )

Здесь интегрирование в правой части ведется по всему сечению вихря.

Направим ось г вдоль оси вихрей, тогда вектор р в интегралах (18) будет иметь компоненты х и у, а вектор г — х₀ и у₀. Так как область сверхпроводящих токов и магнитных полей в вихре имеет размер порядка X, функции nv_x и nv_y можно разложить в ряд Тейлора по х и у до квадратичных слагаемых.

Получившиеся интегралы удобно вычислять в цилиндрических координатах. Учитывая при интегрировании по частям, что поле вихря затухает на бесконечности быстрее экспоненты [9], а поток, охваченный вихрем, равен кванту Фо, |у(0)| = 0, ]х;/(0)| = I, и используя стационарное уравнение (14), после векторных преобразований получаем

5²Р ЭЕ с² (    1      {      ₂ ,

—™ = сг— +---~ Е + -фп х(от + Л Д(от))

В уравнении (18) учтено, что полный микроскопический ток равен сумме токов сверхпроводящей и нормальной компонент, а последняя подчиняется закону Ома. Последнее слагаемое в формуле (18), зависящее от скорости вихрей, можно рассматривать как дополнительное поле, создаваемое движущимися вихрями: Ev - Фо х (от + + Х^Дпх^/с. Возьмем ротор от правой и левой частей этой формулы. Учитывая, что постоянный вектор Фо перпендикулярен векторам v и grad п, получим после несложных векторных преобразований rot Ev = Ф0{(у + l2D(nv)/n)Vn + «V(v + 12Д(иу)/и)}/с = ®odiv(nv + A2A(nv))/c.

Продифференцировав по времени уравнение (15) и взяв от него лаплассиан, ограничиваясь вторыми производными, с учетом уравнения непрерывности для вихрей dn/dt = — div (/iv),                                  (19)

получим SB/dZ — X²A(dB/5Z) = — ®_odiv (nv). Соответственно

A(dB/St) = 5(АВ)/5Г = Ф05(Дл)/ЗГ = - Ф0A(div(дv)) = -Фо div(A(»v)).

Таким образом, rot E_v = — (1/с) ЭВ/dr, что совпадает с уравнением Максвелла и подтверждает применимость формул (15) и (18).

При движении однородной решетки вихрей с постоянной во времени и пространстве скоростью в сверхпроводнике без внешних полей формула (18) переходит в известную формулу Е = Bxv/c [9], которую можно вывести из преобразования Лоренца [4 - 6]. Действительно, в системе, связанной с однородным во времени и пространстве потоком вихрей, все вихри покоятся, и электрическое поле отсутствует. Если же концентрация вихрей и их скорость являются функциями времени и координат, в любой инерциальной системе отсчета часть вихрей будет двигаться с переменными скоростями, следовательно, будет присутствовать дополнительное электрическое поле.

При выводе формулы (18) предположений о характере движения вихрей, кроме нерелятивистских скоростей, не делалось, однако не учитывался эффект Холла. Поскольку уравнение непрерывности в форме (19) не применимо в области зарождения или исчезновения вихрей, граница сверхпроводника требует особого рассмотрения.

Ток нормальной проводимости в сверхпроводнике учтен в правой части уравнения (7) как обобщенная сила трения [8]. Можно найти эту силу в явном виде. Нетрудно показать, что магнитный момент М единицы длины вихря равен Ф₀/(4л). Поскольку сверхпроводящая компонента, создающая этот момент, не обменивается энергией с нормальной компонентой, поле В,, создаваемое токами нормальной проводимости, можно считать внешним для этого момента. Если сверхпроводник однороден вдоль оси г, то поле В_п = ВД и магнитный момент М направлены вдоль 2- Воспользовавшись формулой для силы, действующей на магнитный диполь во внешнем поле [5], получим f_z = grad (MB,,) = Afgrad B_n = Afi x rot B„ = Ф_о x \Jc.               (20)

Отметим, что сила, действующая на вихрь со стороны токов нормальной проводимости, направлена противоположно силе, действующей со стороны сверхпроводящих токов [9]. Это естественно, поскольку поле, формируемое сверхпроводящими токами, не является внешним по отношению к вихрю. Считая, что ток нормальной проводимости подчиняется закону Ома, получим выражения для силы трения, действующей на единицу длины движущегося вихря, f_f= о„Ф₀ х Е₀/с = — r,v, где В_о и Е_о = В_о х v/c - магнитное и электрическое поля в центре вихря, соответственно р = о_ппФ₀5₀/с² -коэффициент электромагнитной вязкости. Он приближенно пропорционален среднему магнитному полю В ~ B_Q [9].

Линейная восприимчивость

Пусть в сверхпроводнике, в котором внешним источником, например транспортным током, задано распределение вихрей л₀(г), распространяется плоская гармоническая волна В(г, /) = 15_mexp(zkr — zoi). Она создаст в сверхпроводнике гармонические волны скоростей v(r, г) и концентраций лДг, t\ При этом в уравнении (18) и(г, Г) = п₀(г) + л^г, f), т. е. переменная составляющая концентрации вихрей порождает вторую гармонику электрического поля. При анализе линейной восприимчивости будем считать, что В_т « В_о, где S₀(r) — стационарное распределение магнитного поля в сверхпроводнике, соответствующее распределение вихрей и₀(г), соответственно (л^г, ?)| « л₀(г). Поэтому в уравнении (18) положим п(г, t) = п₀(г\

Будем считать, что в стационарном состоянии вихри закреплены на центрах пиннинга, а под воздействием волны колеблются около этих центров, не переходя в режим течения потока. При этом внутри сверхпроводника вихри не зарождаются и не исчезают. Воспользуемся моделью коллективного пиннинга упругого вихря на распределенных дефектах [9]. Проводя усреднение (3) сначала по оси z, вдоль которой направлен орт 1, а потом по сечению S, перпендикулярному этому орту, получим на первом этапе линейные вихри, ориентированные вдоль оси z, с равномерно распределенной силой пиннинга.

Положим, что сила пиннинга, действующая на единицу длины вихря, равна f = —ди + />|ири. Здесь и — смещение вихря от положения равновесия. Коэффициент нелинейности b учитывает, что при достаточно большом смещении вихрь отрывается от центра пиннинга. В линейном приближении будем считать |и| малым и положим 6 = 0. Учитывая известную формулу [9] для силы, действующей на единицу длины вихря со стороны сверхпроводящих токов j_s, обтекающих кор вихря, и формулу (20), запишем уравнение движения вихря в виде

fl« = 0, “U ХФ(Л

Усредним это уравнение по сечению физически малого объема. Так как v = Su/dl, для средней скорости получим

1 f 5²Р „ 5Е ] _Л v = — —г ^_ 2<т„ — х Ф_о

St" dt J

Подставляя это соотношение в формулу (18), получим а2

й2

р.^Мр-^д^р) 4лиЛ" I

4.tZ

л

Е + сг — Е- ' 5/

Ф(’/7(

2ж?Л2

Е--дОцЕ)

Если в неоднородной среде распространяется плоская гармоническая волна постоянной амплитуды E(r, /) = E_oexp(zkr - №t), то из формулы (1) следует, что волна обобщенной поляризации также будет плоской и гармонической, но, в общем случае, с переменной в пространстве амплитудой: Р(г, г) = х^со, ^k- ^r)E₀ e^O'kr - /о/), где

i(®,k.r) = р/г jjp(r,p,r)ap(- /кр + кот^Р -

Фурье-образ обобщенной восприимчивости (1), часто называемый комплексной восприимчивостью. Введенная таким образом восприимчивость позволяет определить обобщенную проницаемость г(<чк,г)=1+4^(бу,кг), которая связывает комплексные амплитуды плоских гармонических волн электрического поля и обобщенной индукции О(г) = ф,к,г)Е₀-

Для плоских гармонических волн уравнение (21) принимает вид

ZE-

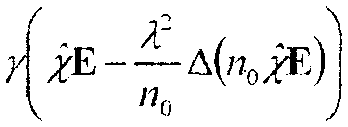
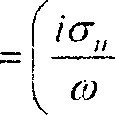
|Е- у      Е - — Д(»_ОЕ)

4 личу' J со \

Фо^о где обозначено у = ---ту

. Для жестко закрепленных на центрах пиннинга вихрей

4 ла л

О",, С² со 4лй²®²

(сверхпроводник третьего рода) при а -»ос получаем z(cy,k,r) = z0(

т. е. пространственной дисперсии нет. Обобщенная проводимость ст = -/®Z = соответствует комплексной проводимости сверхпроводника в рамках двухжидкостной модели и описывает проникновение электромагнитного поля на глубину

. с- _           .     _|3 ,

Jl + H^J^ ’ где ~ 4лй2<7 "    ~— частота, на которой сравниваются токи сверхпроводящей и нормальной компонент [9].

Будем искать решение уравнения (22) для случая малой концентрации сильно связанных вихрей при у « 1 методом последовательных приближений по малому пара метру у: /(сдк.г^/д^д^+у/^сдк.г), тогда ^Е- /0    ~ K^oE-^'A^qE)), и для плос кой волны получаем

2! («- Е, г) = - — + -4г-т («о + 2² (F л . - 2/kVи₀ - Ал, ( го ^лКаг J

Для металлического сверхпроводника в радиочастотном диапазоне А2 А:2 << 1. Для сверхпроводников со значительной силой пиннинга характерны треугольные распределения концентрации вихрей [9]. Лапласиан такого распределения равен нулю всюду, кроме точки излома, и при усреднении можно положить А2Дп0 << п0. Поэтому выражение для обобщенной проницаемости жесткого сверхпроводника имеет вид

Дсдк.г ) = 1 + —-— --1 —;—- — +1   -2/2'kVwn)          /733

л to" \ to, ) Л" и л го Х^со,, )                                  ' ’

Из формулы (23) видно, что пространственная дисперсия проявляется в неоднородно намагниченных сверхпроводниках. При этом и действительная, и мнимая части обобщенной проницаемости зависят от угла между волновым вектором к и градиентом концентрации вихрей, т. е. направлением транспортного тока. Особенно сильно влияние пространственной дисперсии на волну, распространяющуюся в направлении градиента концентрации вихрей.

В сверхпроводящей пластине увеличением транспортного тока и его последующим уменьшением до нуля можно создать распределение вихрей, когда у поверхности концентрация равна нулю, а градиент ее максимален и определяется критическим током [9]. В этом случае в приграничной области даже при слабом пиннинге, т. е. большой величине Ф‘/а, параметр у будет мал и применимо представление (23). Тогда при

1 V7       аЮ'

выполнении условия KV,7o > для волны, распространяющейся в глубь сверхпро водника, действительная часть обобщенной проницаемости положительна, а для обратной — отрицательна.

Строго решить задачу о распространении волны в направлении градиента, т. е. изменения параметров среды, достаточно сложно. В таких неоднородных средах возможны, например, продольные волны, для которых Е = к^. Для плоской продольной волны второе уравнение Максвелла (2) принимает вид t/h D = <2A’(?(r)E)=Egra(s)+ffkE = 0 , т. е. kV? = -к'Е . При со << ю_Л из уравнения (23) следует, что для продольных волн Ф²

k = —"^^Пи ’ что достижимо в приграничной области.

Для противоположного случая большой концентрации слабо запиннингованных вихрей уравнение (22) можно решать методом последовательных приближений по малому

_ 4ж?Л2

параметру 7 - ф2_п^:

/ , \ . 8я7сг 16я²аЛ²    ( i2

гДсдк,г)= 1 +--- + ——7--—и —- +--—7

со Ф’ч₀^ + Л‘А'Д со 4яЛ"со'

В пределе свободных вихрей (а -> 0) получаем чисто мнимую восприимчивость, т. е. движение вихрей в сверхпроводящей фазе просто удваивает потери в нормальной фазе. Это вполне естественно, поскольку в идеальном сверхпроводнике второго рода потери возникают на сколь угодно низких частотах [9]. При со « ор обобщенная проницаемость (24) почти действительная и положительная. Если у = 0,1 и X = 10“5 см, то на частоте го = 106 с”1 е ~ 1020, коэффициент преломления порядка 1010, что соответствует волновому числу к = 105 см1 ~ 1Д.

Этот результат свидетельствует о приближенности формулы (24). При таких значениях волнового числа поле в физически малом объеме, по которому производилось усреднение, оказывается существенно неоднородным и может стать неприменимым исходное уравнение (21). Нелокальность связана с тем, что при значительной амплитуде колебаний слабо запиннингованных вихрей на их движение влияет поле на расстоянии от центра пиннинга существенно большем, чем к. Для анализа пространственной дисперсии в таком случае следует учитывать больше членов разложения при вычислении среднего поля и тока (18) и применять кинетический метод [13] с помощью функций распределения, рассматривая слабый пиннинг как малое возмущение лагранжиана (5).

Заключение

Уравнения динамики абрикосовских вихрей, полученные с помощью формализма Лагранжа, позволяют рассматривать электромагнитные процессы в сверхпроводниках второго рода в терминах обобщенной индукции. Несмотря на создаваемую транспортным током анизотропию, обобщенные проницаемости (23) и (24) являются скалярными, т. е. продольная и поперечная проницаемости равны. Следовательно, магнитная проницаемость сверхпроводника (дифференциальная, поскольку рассматриваются малые амплитуды) равна единице [5]. Это соответствует рассмотренной модели колебания вихрей возле центров пиннинга. При таком движении намагниченность не меняется.

Изменение намагниченности и, соответственно, тензорный характер обобщенной проницаемости проявятся в режиме течения потока. Анализ пространственной дисперсии при таком движении вихрей требует применения кинетических методов [13]. Однако уже полученные выражения для обобщенной восприимчивости показывают возможность нескольких типов волн - продольной, замедленной, пусть и не в такой степени, как следует из формулы (24). Возможность электрического управления дисперсионными характеристиками таких волн и анизотропией среды с помощью транспортного тока и внешнего подмагничивания, задающих нужное распределение вихрей, позволяет применять их в устройствах функциональной электроники подобно спиновым волнам [10].