Нелокальная по времени краевая задача для линеаризованной системы уравнений фазового поля

В ограниченной области Q с R n с границей dQ класса C ” рассмотрим линеаризованную систему уравнений фазового поля

—( x , t ) + 1 — ( x , t ) = к А v ( x , t ) + g^ ( x , t ),         ( x , t ) eQx [0, T ],                (1)

d t      ^z d t ¹

A w ( x , t ) + a w ( x , t ) + e v ( x , t ) + g ₀ ( x , t ) = 0,       ( x , t ) eQx [0, T ],                (2)

в которой для двухфазной среды связываются температура v относительно температуры равновесия между фазами и фазовая функция w . В предположении нулевого времени релаксации эта система уравнений описывает фазовые переходы первого рода [1, 2]. Здесь 1 - скрытая теплота, к - коэффициент теплопроводности, g 1 - функция внешнего теплового источника, константы а , в и функция g ₀ определяются соотношением фазового поля, вводимым на основе теории фазовых переходов.

Снабдим задачу нелокальными условиями по времени

T jv (x, t )n( t) dt = v0( x), x eQ,(3)

T j w(x, t)n(t)dt = w0(x), x eQ,(4)

и граничными условиями при 6 e R

6—(x,t) + (1 - 6)v(x,t) = 6w(x,t) + (1 -6)w(x,t) = 0, (x,t)edQx[0,T].(5)

∂n∂

Нелокальная задача в банаховом пространстве

Рассмотрим сначала нелокальную задачу

T j u (t )n( t) dt = u 0(6)

для вырожденного эволюционного уравнения в банаховом пространстве

Lu'(t) = Mu(t) + g(t), t e [0,T].(7)

Здесь U и V - банаховы пространства, L e L(U; V) (т.е. линейный и непрерывный оператор из U в V), ker L Ф {0}, M e Cl(U; V) (т.е. линейный, замкнутый, плотно определенный в U, действующий в V оператор), g: [0, T] ^ V. Введем обозначения pL (M) = {p e С :(pL - M)-1 e L(U; V)}, UL (M) = С \ pL (M),

R . ( M ) = ( . L - M ) ^{- 1} L , L . ( M ) = L( . L - M ) ^{- 1}.

Определение 1. Пусть p e N u {0}. Оператор M называется сильно (L, p) -радиальным, ес- ли

(i)  3a e R (a, +~) c pL (M); (ii)    3K > 0 V.e (a, +~) Vn e N max {| R.M)) • < p+ L(u JL. (M» n(p+1)| L (V) }< . Kn..

• (iii)    существует плотный в V линеал V такой, что при любом .e ( a , +~ )

|| M( . L - M ) ^{- 1}( L . ( M )) ^{p + 1} f\\ v < co’st f )₂    V f e V;

( . - a ) ^p

(iv)

\\( R . ( M )) ^{p + 1}( . L - M ) ^{- 1}\ L ( v ; u ) <

K

( . - a ) ^{p + 2}

при любом .e ( a , +~ ).

Замечание 1. Если U и V - рефлексивные банаховы пространства, то выполнение условия (iii) следует из выполнения условий (i), (ii), (iv).

Положим U ⁰ = ker(R . ( M )) ^{p + 1}, V⁰ = ker( L . ( M )) ^{p + 1}; U ¹ - замыкание образа оператора im( R . ( M )) ^{p + 1} в пространстве U , V¹ - замыкание образа im( L . ( M )) ^{p + 1} в пространстве V. Обозначим через L k ( M k ) сужение оператора L ( M) на U k ( D ( M k ) = D ( M ) n U k ), k = 0, 1.

Теорема 1 [3]. Пусть оператор Mсильно ( L , p )- радиален. Тогда

• (i)   U = U ⁰ © U¹, V = V⁰ © V¹;

• (ii)    L k e L (U^k ; V ^k ), M k e Cl ( U^k ; V ^k ), k= 0,1;

• (iii)    существуют операторы M - ¹ e L (U ⁰; V⁰) и L - ¹ e L (V¹; U¹);

• (iv)    оператор H = M ₀ ¹ L ₀ нильпотентен степени не больше p ;

• (v)    существует разрешающая уравнение Lu '( t ) = Mu ( t ) вырожденная сильно непрерывная

полугруппа операторов { U ( t ) e L (U ): t >  0 } ;

• (vi)    оператор    L 1 ^- 1 M 1     порождает    C 0 -непрерывную   полугруппу операторов

{ U 1 ( t ) = U ( t )^ 1 e L (U 1 ): t >  0 } .

Обозначим проектор вдоль U ⁰ на U ¹ через P и проектор вдоль V⁰ на V¹ через Q .

Определим характеристическую функцию нелокальной задачи (6)

T

Х ( z ) = J е^Й П ( t ) dt ,                                           (8)

которая, как известно [4], является целой .

Следуя работе [5], в случае сильно (L, p)-радиального оператора M обобщенным решением уравнения (7) будем называть функцию tp

u ( t ) = U ( t ) v + J U ( s ) L - ¹ Qf ( t - s ) ds - ^ H^kM 0 ¹ (( I - Q ) f )^{( k} ) ( t )

0                           k = 0

при Qf e C ([0, T ]; V), ( I - Q ) f e C p ([0, T ]; V) для любого v e U.

Функция u e C 1 ([0, T ]; U ) n C ([0, T ]; D ( M )) называется классическим решением уравнения (7), если для нее выполняется равенство (7). Классическим (обобщенным) решением задачи (6), (7) называется классическое (обобщенное) решение уравнения (7), если для него выполняется условие (6).

Теорема 2 [5]. Пусть выполняются следующие условия:

• (i)    оператор M сильно ( L , p ) -радиален и непрерывно обратим;

Математика

• (ii)    пе C 1 [0, T ], n (0) * 0;

• (iii)    ни один нуль характеристической функции % не принадлежит L-спектру a L ( M ) оператора M ;

• (iv)    L -^ Qf е C ([0, T ]; D ( M )), ( I - Q ) f е C^p ([0, T ];V);

Tp

• (v)    ( I - P ) и 0 = - J^ H^kM 0 ¹ (( I - Q ) f )^{( k} ) ( t ) n ( t ) dt .

0 k = 0

Тогда

• (i)    для Pu ₀ е D ( M 1 ) существует единственное обобщенное решение и е C ([0, T ]; U ) задачи (6), (7), при этом

II ullc ([0, T ];U) - C [lIMPu o|Iv +| IL- Qf\\c([0, T ]; D (M)) +11( I - Q ) fllcp ([0, T ];V) j, где константа С не зависит от и0 и f;

• (ii)    если Pu ₀ е U ¹ \ D ( M 1 ), то не существует обобщенного решения задачи (6), (7);

• (iii)    при L - Qf е C ([0, T ]; D (( L j"¹ M 1 )²)), ( I - Q ) f е C^{p + 1}([0, T ];V), пе C ²[0, T ], обобщенное решение задачи (6), (7) является классическим тогда и только тогда, когда Ри ₀ е D (( L-^x M 1 )²) .

Редукция исходной задачи к общему случаю

Вернемся к задаче (1)-(5). Положим U = V = ( L ₂( Q ))²,

L=

Г1 1)

е L (U ), ( 00 j

M=

г

и ( t ) =

[

v ( - , t ) 1

I , t ^ 0, w ( - , t ) j

(кА 0

В«^ Iе Cl(U>• [ в a ।

g

f = g1I,

[ g 0 j

H 2 ( Q ) = J У е H ²( Q ): | 9 —+ 1 - 0 | y ( x ) = 0, x едQ^ , D ( M ) = ( H j ( Q ))²,

" Г [ dn У'

h 9 ( Q ) = J y е H ⁴ ( Q ): 9 -^ A ^ky ( x ) + (1 - 9 ) A ^ky ( x ) = 0, x е dQ , k = 0,1 1 .

I               dn

Рассмотрим оператор Ay = A y , D ( A ) = H 2( Q ) c L ₂( Q ). Обозначим через { ^ _k : k е N } орто-нормированные в смысле скалярного произведения (• , -^ в L ₂( Q ) собственные функции оператора A , занумерованные по невозрастанию собственных значений { 2 k : k е N } с учетом их кратности.

Теорема 3. Пусть -a + @ 1 й ^ ( A ), к >  0. Тогда M - сильно ( L ,0) - радиальный оператор.

Доказательство. Используя разложение по базису { ^ _k : k е N } в пространстве L ₂( Q ) и обо- „   кХ_к ( а + 2 )

значение ок = —k-----—, получим операторы k α-βl+λk

( p L - M ) ^{- 1} =

∞ k=1

те

Z

[ k = 1

' p - S2\ pl ^

, - @ - a -A j , ^{(- a - 2}k ) (^-, ^ k ) ^ k у      - P ¹ (^-, ^ k ) ^ k     '

(-a+@1 - 2k )(p - Sk) Й(-а + @1 - 2. )(p - Sk)

^{в - ,} Ф к ^Фк     у ⁽ P ^{- 2} ) •^,-АРк ^Фк

(-a+@1 - 2k )(p - Sk) h(-a + @1 - 2k )(p - Sk) j

µ L - M =

е L (V; U ),

R ^ ( M ) =

∞

I

к = 1

TO

I

V к = 1

^{(- a - A}k ) ( Ф >k ( -a + 8 / - A k )( ц - 5 k )

⁸ • ^, Ф k ) ф k

∞

I

к = 1

∞

^{(- a - A}k ) ^/ { - Ф Фк ^ф Фк "  ( - a + 8 / - A k )( ц - 5 k )

p/ к>Фк >k

e L (U ),

I, ^{(- a} + ^ ^{- A}k ^{)( ц - 5}k ) k = 1 ^{(- a + в} - ^Ak ^{)( Ц} - ⁵k )

L ^ ( M ) =

∞

I

к = 1

µ - δ _k

∞

I

к = 1

^{- KA}k^/ (• ^, Ф k ^фk    )

(-a + в/ - Ak )(ц - 5k) e L(V),

V

∞

I

0                 0

^{(- a - A}k ) C ^ k M

∞

I

^{(- a - A}k X- A ) ^/ {■ , ф к ) ф к )

R^l_m ( M) Ц - M ) ^{- 1} =

k=1(-a + в — Ak )(ц - 5k )2 ^ (-a + в - Ak )2(ц - 5k )

. 2

∞

вФфк

V k=1(-a + 8 - Ak )(ц - 5k)

у   P( A )/ к'ФРк >k f=1(-a + 8 - Ak )2(ц - 5k )

∞

•

12 7

В условиях теоремы a = max 5 < + ^TO , k ∈ ℕ ^k

min |- a + 8 / - A l >  0, max k ∈ ℕ              ^k        k ∈ ℕ

max

- α - λ _k

-α+ βl -λk

< to , max

( -a - A k X-A ) /

^{k e} N ( - a + в - A _k )

- κλ _k l

k ∈ ℕ - α + β l - λ _k

< to ,

max

β

- κλ _k l

< to, max keN (-a + ^ - Ak)

k ∈ ℕ - α + β l - λ _k

Следовательно, существует K >  0, такое, что для всех ц >  а ,

< to ,

< to .

max { | R ( M )| L ₍ u ) ,\\L^L _M ( M )| L _{( V} ) } <----- ,    р Ц ( M )( ц L - M ) ^{- 1} | L _{( V ; M} )<  ------- •

^{L                             J} ц - а                                    ( ц - a )²

Таким образом, с учетом гильбертовости пространств U и V, в рассматриваемой задаче оператор M сильно ( L , p )-радиален (см. замечание 1). •

Полугруппа системы может быть найдена по формуле [3] U ( t ) = s -

lim ( ( n11 ) R L _t ( M ) ) n n →∞

Имеем

( ( n / 1 ) R L / ₁ ( M ) ) n

у ⁽ n / t ) ^{( a A}k ) (", ^фк ^фФк у

I      /-Л» I к=1 /        Qi 1x1 n I к=1

(-a+p/-Ak)I --5k |

⁽ n / t ) ^{n ( -a - A}k ) ^/ (,-pp_k ^фф _к ^Л

n

n

^{(- a + в - A}k ) I —^{- 5}k I

Поэтому

U ( t ) =

у     ⁽ П / t ) n ⁸-, P k ^фФк

I.      r„v к=1 / Ql 1 X | n O |

^{(- a + в - A}k ) I -^{- 5}k I

V                    ^V t ⁷

у    ⁽ n / t ) n ^в ■ ( Ф Рк ^фФк

I              n к=1 /        Ql ixl n I

^{(- a + в - A}k ) I -^{- 5}k I

V t 7 7

•

^∞ I^; k =

∞

I

V к = 1

e^5k k^{( -a - A}k )

- α + β l - λ _k e δ k t _β

-α+ βl -λk

- e ^{5 k} ( - a - A ) / < ^Р‘>^{Ф к} I OPp-A;

∞ e δ k t _βl

<^{РФ к} I apnA^{

\

•

Следуя работе [5], обобщенным решением задачи (1)-(5) будем называть вектор-функцию

U ( t )

∞

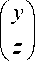
I e

• ^5kt ( - a - A k )

k =,-

∞

^I I I

V к = 1

-

α + β l - λ _k e δ k t _β

-α+ βl -λk

∞ к y , Фк ^фФк ⁺ 1- к = 1

∞

-к y ,Фк >k + 1

к = 1

e ⁵ k t ( - a - A k ) /

- α + β l - λ _k e δ k t _βl - α + β l - λ _k

\

Математика

при произвольных y , z e L ₂( Q ). Классическое решение ищется в классе пар функций, каждая из которых лежит в C 1 ([О, T ];L₂( Q )) n C ([О, T ];H ^ ( Q )). Обобщенное решение является классическим, если y , z e H 2 ( Q ), классическое обобщенным является всегда [4, 5].

Проекторы P и Q имеют вид

P = s - lim ( i R i L ( M ) ) 2

∞

I

к = 1

oo

I

V к = 1

^{(- a - X}k ) k-ррк >k I ^{(- a - X}k ) l k-ррк >k

- α + β l - λ _k

вк >k

- α + β l - λ _k

к = 1

∞

I к=1

- α + β l - λ _k ^{в р} >к

Тогда

\

,

-a + в - X k   7

Q = s - _i | i m ( I L L ( M ) ) 2 =

∞ к=1

V О

^KXkl k'PPk >k )

- α + β l - λ _k

О

•

U ⁰ = ker P = { ( v , w ) e ( L ₂( Q ))²

: v = - lw } ,

U

∞

U ¹ = imP = J I

Д к = 1

^{( -а - X}k X ^{v +} lw, Ф к>к ^ ^{вv + lw ,} P k>к ) ,  . ,_Т ^^2

---------"--------'— ' —--------'— :( v , w ) e ( L 2 ( Q )) г ,

- α + β l - λ _k

, I

к = 1

-

-^a + ^e - X k ₇

_v                z_n^2     V ^KXk lkw , Ф к ^фФк

V = ker Q = X v , w ) ^{e ( L} 2^{(q)) :} v = I----^X ^ , t                     k =1 ^-a + P l ^{- X}k J

Сформулируем теорему о разрешимости задачи (1)-(5). Теорема 4. Пусть выполняются следующие условия:

V¹ = imQ = L ₂( Q ) х {0}.

(i)

(ii)

О, - a , -a + в ^ ^ ( A ), к >  О; ne C 1 [О, T ], п (0) * О;

(iii)

X

( KX ( a + X ) ) _{A M}

——---— * О, к e N;

V a - в + X k J         ’

(iv)

(v)

g 1 e C ([0, T ]; H ² ( Q )), g о e C ([0, T ]; H ² ( Q ));

^Kv о = "fI ^KXk^ g ^{o (,} _r t^^{Рк Р к}% )t ) dt , ^e v о ^{( x} ) ^{+ ( a + a)} w o^{( x} ) = - J g о ^{( x} , t ) n ⁽ t ) dt • О k = 1    ^-a + ^в - ^Xk                               О

Тогда

(i) для v _О + lw₀ e H ( Q ) существует единственное обобщенное решение задачи (1)-(5) , при

этом

II v il e ([О, T ]; L 2 ( Q )) ⁺ II w ll c ([О, T ]; L ₂( Q ))

< C ⁽| v о + lw o| H ²( q ) +|| ^g 1| С ([o, t ]; h ²( q ))

⁺ ll ^{g О}1 С ([0, T ]; H ²( Q )) ) ,

где С не зависит от v _О, w ₀, g 1 , g _o;

• (ii)    если v _О + lw₀ e L2 ( Q ) \ H ^ ( Q ), то не существует ни одного обобщенного решения задачи (1)-(5);

• (iii)    при g 1 e С ([О, T ]; H ^ ( Q )), g _О e С ([О, T ]; H ^ ( Q )), ne С ²[О, T ] обобщенное решение задачи (1)-(5) является классическим тогда и только тогда, когда v _О + lw₀ e H ^ ( Q ) .

Доказательство. Согласно теореме 3, оператор M сильно ( L ,0)-радиален, при этом S _k -точки его L -спектра. Поэтому из условия О, - at о ( A ) следует, что 5 _к * О, к e N, и оператор M непрерывно обратим.

Учитывая полученные формулы для проекторов и условия данной теоремы на функции g 1 , g _О, v _О, w ₀, нетрудно заметить, что и остальные условия теоремы 2 выполняются. •