Неминимальные макроскопические модели скалярного поля, основанные на микроскопической динамике. I

В последнее время опубликовано большое количество работ по позднему ускорению Вселенной. Для решения проблемы вторичного ускорения Вселенной во многих работах предлагается коренным образом изменить фундаментальные принципы физики. Однако, сейчас появляются некоторые аргументы в пользу того, что сложные, многокомпонентные, классические физические системы также могут приводить ко вторичному ускорению Вселенной. В частности, такие аргументы были приведены Д. Гальцовым, а также автором статьи в докладах на семинаре Gracos-2009 (см., например, [1,2]). В цитированной работе [2] был приведен пример космологической эволюции полностью вырожденной Ферми-системы со скалярным взаимодействием частиц, с начальной инфляцией и поздним ускорением. В работе В. Журавлева [3] исследовалась космологическая эволюция двухкомпонентной системы, состоящей из идеальной жидкости и скалярного поля. В этих работах показано, что такие космологические модели могут иметь начальную инфляционную стадию и позднее ускорение. Таким образом, космологические модели с многокомпонентной материей в состоянии описать основные наблюдательные данные о расширении Вселенной. Некоторые указания на возможность такого поведения сложных систем со скалярным взаимодействием частиц были даны также в работах [4,5]. В отличие от двухкомпонентной системы «скалярное поле + идеальная жидкость», в которой взаимодействие компонентов осуществляется лишь через гравитацию2, мы рассмотрим статистические системы скалярно заряженных частиц, в которой некоторые сорта частиц могут прямым образом взаимодействовать со скалярным полем через некоторый фундаментальный скалярный заряд. С другой стороны, статистическая система, обладая, вообще говоря, ненулевым скалярным зарядом и сама являясь источником скалярного поля, может эффективно влиять на скалярное поле, управляя его поведением. Такое скалярное взаимодействие было введено в общерелятивистскую кинетическую теорию в 1983 г автором статьи [6-9] и несколько позже - Г.Г. Ивановым [10]. В частности, в работах [7,8] на основе кинетической теории получена самосогласованная система уравнений, описывающая статистическую систему частиц со скалярным взаимодействием. Следует отметить, что в настоящее время создано множество моделей неминимального взаимодействия скалярного поля с обычной материей. В частности, рассматривались модели связи посредством кинетического члена лагранжиана взаимодействия. Однако, все рассматриваемые модели имеют один существенный недостаток - они являются полностью феноменологическими. В отличие от этих моделей мы рассмотрим строгую динамическую модель взаимодействия скалярного поля с элементарными частицами, основанную на микроскопических уравнениях движения Гамильтона и последующей процедурой статистического усреднения. При этом оказывается, что взаимодействие скалярного поля с частицами можно ввести единственным образом, также и макроскопические уравнения материи и скалярного поля с помощью процедур усреднения получаются однозначным образом. Тем самым, устанавливается тесная связь между микро - и макро - уровнями описания скалярного взаимодействия. Вполне естественно, что получающаяся на таком пути модель скалярного взаимодействия должна иметь более сложную конструкцию, чем аналогичные феноменологические модели, но при этом она обнаруживает и более богатые возможности поведения.

Статья посвящена обзору работ Автора и его учеников по исследованию проблемы введения скалярных полей в макроскопическую классическую теорию гравитации.

2.    Динамика частиц со скалярным взаимодействием 2.1.    Канонические уравнения движения

Канонические уравнения движения релятивистской частицы относительно пары канонически сопряженных динамических переменных xi (координат) и Pi (обобщенного импульса) имеют вид (см., например, [7])3:

dxi   ∂H dPi = dH ds      dxi

(2.1)

..=-—； ds ∂Pi rje H(x, P) - релятивистски инвариантная (функция Гамильтона. Вычисляя полную проіізво,甲іуто от функции динамических переменных ^(xi,Pk), с учетом (2.1) найдем:

字= [ H, 加                                 ( 2-2)

ds где введены инвариантные скобки Пуассона:

叱]= Ц 言 -%           (23

∂Pi ∂xi   ∂xi ∂Pi

Вследствие (2.3) функция Гамильтона является интегралом движения частицы:

dH

(2.4)

——=[H, H] = 0, 今 H = Const. ds

Соотношение (2.4) можно назвать соотношением нормировки. Инвариантная функция Гамильтона определяется неоднозначно. Действительно, вследствие (2.3) если H(x, P) — функция Гамильтона, то и любая непрерывно дифференцируемая функция f (H) также является функцией Гамильтона. Единственная возможность введения инвариантной функции Гамильтона, квадратичной по обобщенному импульсу частицы, при наличии только гравитационных и скалярных полей есть следующая:

^{H ( x, P}) = 2 [帆 x)(^P,^P) - 9 ( x) ^] ,                              (2-5)

где¹ (a, b) з,і,есь ii в дальнейшем есть скалярное произведение векторов четырехмерных векторов a ii b ：

(a,b) = gikaibk, a 3(x) 口 夕(x) — ііеко工орш、скалярные (функции. Т1асто константу в правой части (2.4) выбиратот равной 1/2m2. rje m — масса покоя частптіы. Но мы не будем <)того делать, выбирая более удобную, нулевую, нормировку функции Гамильтона [11,12], так как эту константу можно ввести и в (J)yilKTUITO 3(x)：

^H(x,P) = 2 ^[^^(x)(p,P) ^- 9 ( ^x)]=⁰ ・                             (2.G)

Заметим, что в работе автора [6] релятивистски - инвариантная Функция Гамильтона частицы со скалярным зарядом q, находящейся в скалярном поле с потенциалом 夕 вводилась соотношением:

H(x,P) = ， (P, P) - q/                               (2-7)

Несмотря на компактную форму записи эта функция Гамильтона неудобна появлением радикала. В другой работе автора [6] релятивистски - инвариантная функция Гамильтона вводилась соотно-

H (x,P ) = 1 m [ Т - q. l .

2 m + qg

Итак, из соотношения нормировки (2.6) найдем:

(P,P ) = у,                                          ( 2-9)

ψ а из первой группы канонических уравнений движения 2.1 получим связь между обобщенным импульсом и вектором скорости частицы:

u i 三 dx i = 也 P i 今 P i = 也 ^-1u i ,                            (2.10)

ds

Подставляя последнее соотношение в соотношение нормировки (2.9), получим:

(u, u)=也9， поэтому для выполнения соотношения нормировки вектора скорости частицы

(u, и) = 1.                                                 (2.11)

должно быть:

^у = 1 今 ^ = у^-1,

• -таким образом, инвариантная функция Гамильтона частицы может определяться лишь одной скалярной функцией g(x). Учитывая последнее соотношение, запишем функцию Гамильтона в окончательной форме:

^H(x,P) = 2 [ уТ(^х)(^р,^р) — g^(x) ] = О,                         (2-12)

и из канонических уравнений (2.1) получим связь между обобщенным импульсом и вектором скорости частицы:

Pi = gdxi.                                         ( 2-ІЗ)

ds

Из определения (2.5) следует , что вектор обобщенного импульса времениподобен:

⑵ 14)

(P,P ) = у2.

Отметим полезное для дальнейшего соотношение, являющееся следствием (2.3), (2.5) и (2.14):

[H,P ^k ] = v k g 三 g ik& y.

⑵ 15)

• 2.2.    Уравнения движения в Лагранжевой формулировке

Из второй группы канонических уравнений (2.1) получим уравнения движения в Лагранжевой формулировке [13]:

d2xi     i dxj dxk f + jk石石

d ,k ln |y|P ik ,

⑵16)

где:

P ik = P ki = gik - uiuk                                  (2.17)

—тензор ортогонального проектирования на направление и, такой что:

P ikuk 三 0 ； P ikgik 三 3 .                                   (2.18)

Из этих соотношений и уравнений Лагранжа (2.16) вытекает строгое следствие ортогональности векторов скорости и ускорения:

iduk gik u工三°.

⑵19)

Заметим, что лагранжевы уравнения движения (2.16) инвариантны относительно знака скалярной (j)yilKTHIII g(x):

g(x) т -g(x).

(2.20)

Также инвариантна относительно преобразования (2.20) и функция Гамильтона (2.12) при нулевой ее нормировке. Поэтому из соотношений (2.14), (2.13), а также уравнений Лагранжа (2.16) следует, что модуль скаляра 夕 имеет смысл эффективной инертной массы частицы, m*, в скалярном поле:

0 = m*

(2.21)

Заметим, что указанному выбору функции Гамильтона соответствует следующая функция действия:

S

m ∗ ds,

(2.22)

формально совпадающая с функцией Лагранжа релятивистской частицы с массой покоя m* в гравитационном поле (см., например, [14]).

• 2.3.    Интегралы движения

Найдем теперь условия существования линейного интеграла канонических уравнений движения (2.1), связанного с полными энергией и импульсом частицы, для чего вычислим полную производную по каноническому параметру от скалярного произведения (£, P). Используя канонические уравнения движения (2.1), соотношение нормировки (2.14), а также связь обобщенного импульса с кинематическим (2.13), найдем:

d( 《, P) ds

—PiPk L’gik + Lm* ,

(2.23)

гж1 L — проігзволная Ли по иапра.влсчшто £ ξ

4. Полагая далее

d(£,P) ds

0 О (£, P) = Const,

(2.24)

с учетом произвольности вектора обобщенного импульса и соотношения нормировки для него, получим условия выполнения этого равенства:

L gik = ^pgik 今 ^p ξ

—Lln |m*|. ξ

(2.25)

Подставляя этот результат обратно в соотношение (2.23), получим окончательно необходимые и достаточные условия существования линейного интеграла канонических уравнений движения (см., например, [13]):

L m ∗ gik ξ

(2.26)

Таким образом, для того, чтобы существовал линейный интеграл канонических уравнений движения (2.1) необходимо и достаточно, чтобы конформно соответствующее пространство с .метрикой m*gik допускало группу деиж’ений с вектором Киллинга & Заметим, что липе иные интегралы (2.24) имеют смысл полного импульса (при пространственно-подобном векторе £) или полной энергии (при временно-подобном векторе £).

4См., например, [15].

2 ・ 4 ・ Выбор функции массы

Возникает вопрос о выборе функции т*(Ф). Не конкретизируя пока эту функцию, отметим следующее важное обстоятельство. Рассмотрим статические поля gik и Ф, допускающие времениподобный вектор Киллиига £i = 84, когда сохраняется полиая энергия частицы, P4. Рассмотрим далее систему отсчета, в которой g@4 = 0, так что координата х⁴ совпадает с мировым временем t. Тогда, из сооттюіпетшіі связи между вектором кішематіг-ісч/коп скорости ui 11 вектором полного импульса частицы В (2.13) следует:

Rds = m*dt, (2.27)

rje P4 = Eo = Const > 0 - полная эіі ( ?ргпя ^заряженной частицы. Полному, если мы хотим сохранить одинаковую ориентацию мирового и собственного времени (т.е., dt/ds > 0), необходимо выбрать такую функцию массы, которая всегда бы оставалась неотрицательной:

m* > 0.

(2.28)

Как видно, например, из уравнений Лагранжа (2.16), эту функцию удобно выбрать так, чтобы:

т*(Ф) = |т*(Ф)| > 0. (2.29)

Далее, с одной стороны, в отсутствие скалярного поля, точнее, в постоянном скалярном поле, функция массы должна переходить в массу покоя частицы, m > 0. С другой стороны, уравнения Лагранжа (2.16) в случае слабого скалярного поля должны переходить в классические уравнения движения в скалярном поле. Таким образом, исходя из принципа соответствия, мы должны иметь:

m*(0) = m;     (m*),k | ф=о = q@,k,                              (2.30)

где¹ q — некоторая ( 1 ) упдамепталыіая константа — сшлярный заряд ча.ст/ш^ы. Условия (2.30) о ： зиача-ют, что при малых значениях скалярного потенциала Ф фуикция т*(Ф) должна иметь разложение вида:

т*(Ф)ит(1 + — + ..).                                (2.31)

m

Этому условию соответствует и использованная в цитированных работах линейная функция т*(Ф) = |m + qФ|.

Можно предложить и другой, более радикальный подход, который при этом не противоречит соотношениям (2.30) и (2.31), полагая что вся инертная масса частиц возникает вследствие взаимодействия со скалярным полем:

д(Ф) 三 m* = | qФ | .

(2.32)

Тогда под массой покоя частицы, mo, следует понимать ее массу (2.32) на современной стадии эволюции Вселенной, которой отвечает скалярный потенциал Ф°: mo = m*(Ф(to)). Такому выбору (функции ф(Ф) соответствует (функция действия ：

S

У | qФ | ds.

(2.33)

Этот выбор отвечает и эстетическим критериям, так как в этом случае функция Гамильтона (2.5) не зависит от массы покоя. С другой стороны видно, что при выборе функции д(Ф) в форме (2.32) уравнения Лагранжа (2.16) становятся симметричными относительно замены Ф т —Ф и при условии q = 0 вообще не зависят явно от скалярного заряда，： d2xi     i dxj dxk ds2     jk ds ds

(ln |Ф|),кPik,

(2.34)

При выводе уравнений (2.34) мы учли дифференциальное тождество: d|y| = y/|y|dy. Однако, посредством соотношения нормировки (2.14) зависимость решений от скалярного заряда все же сохраняется и при таком выборе функции массы в виде зависимости энергии от импульса 巳( P2).

• 2.5.    Пример одномерного движения

Рассмотрим следующую задачу. Пусть в пространстве Минковского имеется статическое скалярное поле, потенциал которого зависит только от одной координаты, x¹ = x, и пусть для простоты m* = |qФ| = |x|. Таким образом, пметотся 3 вектора Киллпига - один времениподобный п два пространственноподобных:

'                             一                   gi= 64; gi= 62; gi= S3.

Соответственно этим векторам Киллинга существуют три линейных интеграла движения:

P2 = P0 = Const ; P3 = P3 = Const ; P4 = P0 = Const.              (2.35)

Пусть для простоты P2 = P3 = 0. Тогда с учетом соотношения нормировки (2.14) получим из канонических уравнений движения одно нетривиальное:

dx     д/Р2 — x²

(2.36)

—=干.....

dt         P 4

Положим для простоты P4 = 1, x(0) = 1/2. Тогда в уравнении (2.36) необходимо выбрать отрицательный знак в правой части. Решение этого уравнения есть:

x = cos(t + п/3);

(2.37)

• —и описывает гармонические колебания в мировом времени t; при этом обобщенный импульс, В также является гармонической функцией мирового времени:

3.    Статистические системы частиц со скалярным взаимодействием

Pi = sin(t + п/3).                                       (2.38)

Однако, координаты 4-х мерного вектора кинематической скорости частицы, ui u1 = g 三—R/夕=— tan(t + п/3) ds претерпевают разрывы 2-го рода в моменты времени t = п/6 + пк, в которые x = 0. Это свидетельствует либо о разрыве связи между координатами и собственным временем в указанные моменты мирового времени, либо о необходимости переопределения собственного времени для скалярно заряженных частиц. Для кинематического импульса частицы, pi, если мы введем его как dxi

(2.39)

p = m* 17 三 P， такой проблемы не возникает, как и для трехмерной скорости va = ua/u4. Заметим, что, фактически, лишь эти непрерывные величины и являются физически измеримыми. Тем не менее, указанный пример показывает, что необходимо аккуратно проводить вычисления для скалярно заряженных частиц.

В дальнейшем мы будем пока не будем конкретизировать нормировку эффективной массы, полагая лишь выполненным соотношение (2.29).

Перейдем теперь к описанию макроскопического скалярного взаимодействия. Это описание можно получить с помощью процедуры введения инвариантных функций распределения тождественных частиц.

• 3./ . Функция распределения u макроскопические плотности потоков

Пусть F(x, P) — инвариантная (функция распределения частпті в 8-мерном (разовом пространстве ii пусть 3(x ， P) — некоторая тензорная (функция динамических переменных (x, P). Согласно [13] каждой тензорной динамической функции может быть поставлена в соответствие макроскопическая плотность потока:

WYx)= / F(x,P)3(x ， P)^dHdP 三 m-1 / F(x,P)^(x,P)PidP, P(x)                   ∂P               P(x)

Определим согласно (3.1) моменты относительно распределения F(x, P) [6]:

ni(x) = /   F(x, P) ^dHdP 三 m-¹ /   F(x, P)PidP,

P (x)           °Pi               P (x)

(3.2)

вектор плотности потока числа частиц , так что:

ni = nvi,

(3.3)

где vi — в^юмеипподоопып едіііііг-шыіі вектор кішема.тіг-іескоіі макроскошг-ісскоіі скорости частиц;

n = д/(n, n).

(3.4)

Далее:

]( ， )=/  F(x,P)Pi^HdP 三 m-¹ / F(x,P)PiPkdP,

P (x)            dpk              P (x)

(3.5)

-макроскопический тензор энергии-импульса (ТЭИ). След этого тензора можно вычислить с помощью соотношения нормировки (2.14):

Tp ≡ gikTp^ik

m* / F(x, P)dP.

(3.6)

Инвариантный элемент объема 4-х мерного импульсного пространства в выражениях (3.2), (3.5) в принятой нами системе единиц есть [7]:

_   2S +1 _  _  _  _

(3.7)

dP = /с —    dPi A dP2 A dP3 A dR,

(2п)3，-g где1 S — с пип частицы. Инвариантная восьмимериая (функция распределения F (x, P). сингулярная на массовой поверхности (2.14) связана с несингулярной семимерной функцией распределения f (x, P) С ПОМОШЫО 5-(j)yiIKTIIIII СООТІІОШ(?ІІІІ(?М [7]：

F (x,P) = f(x,P)S(H )= m* "P⁴ - %

(3.8)

rj,e P+ - положительный корень уравнения нормировки (2.14) ： 舛 = g^4kP+ - соответствутоттіее этому корню значение контрвариантной компоненты импульса. В локально-лоренцевой системе отсчета:                                        ________

P ； = 7m* + P²,                                 (3-9)

где P² = £ ： =i(P^а)² — квадрат физического импульса. Таким образом, получим инвариантный элемент объема 3-х мерного импульсного пространства:

е       2S + 1 dPi A dP2 A dP3

三 m*dP°,

(3.10)

dP+=m*函『一可— где

,      _ 2S + 1 dP 1dP 2dP3    _2S + 1 d3P..

dPo = Gg k —P+—三 Gg

Тогда выражения (3.2), (3.5) и (3.6) принимают вид (для простоты записи мы опустили суммирование по сортам частиц):

ni(x)= 2^ / f (x, P)Pi7-gd3P；

P (x)4

Tpk(x) = 2^ / f(x, P)PiPkGg PP;                    (3.13)

P (x)4

Tp = 鴿 ¹ m* / f(x, P ) F3P.                 (3.14)

P(x)4

5Числовой вектор по Дж. Сингу [16].

Таким образом, явная зависимость макроскопических потоков от эффективной массы m* в конечных выражениях исчезает.

• 3.2 . Общерелятивистские кинетические уравнения

Вследствие принципа локального соответствия и предположения о 4-х точечности столкновений частиц, в каждом акте межчастичного взаимодействия сохраняется обобщенный импульс системы взаимодействующих частиц:

Е P i = Е P ' ，                               ( 3-15 )

IF где суммирование проводится по всем начальным, Pi, и конечным,吓，состояниям. Пусть в плазме протекают реакции:

/ mm

£ va 。 a 口 工 vBaB,                          (3 」 6)

A =1        B =1

rj,e a a - символы частить a va - их числа. Таким образом, обобшеішые импульсы начального ii конечного состояний равны:

/ m νA             m νB

P i = ЕЕ PA, P F = ЕЕ P ' B ' .

(3.17)

A =1 a              B =1 a '

Функции распределения частиц определяются инвариантными кинетическими уравнениями [7]:

[H a ^,f a ] = I a (^x, P a ),

(3.18)

(3.19)

где¹ Ja(x,Pa) — интеграл столкиовсипп ：

/

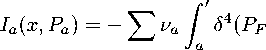
— P i ) W if (Zif — Zfi ) 口 dP ；

I,F где

W_FI = (2n)⁴ | M_IF | ²2^{-E va}+E ^v b

• — матрица рассеяния канала реакций (3.16), (|M /f | — инвариантные амплитуды рассеяния);

• 3.3 • Уравнения переноса динамических величин

Zif = П f(PA9 П Е¹ 土 /(PB" ； Zfi = 口口 土 /■ )] П 〃？£ )，

IF       I    F знак “+" соответствует бозонам, “-" - фермионам (подробности см. в [7,8]).

Строгими следствиями общерелятивистских кинетических уравнений (3.18) являются уравнения переноса динамических величин W&(x, P&) [8]:

Е /(Е

by chanels A =1

▽i ^3 І   ^aFa oj2 dPa -    /   Fa [Ha, ^a]dPa = a 丿 p(x)       dPi         a JP (x)

m'       、 vaWa — Е vBWB 84(Pf — Pi)(ZifWif — ZfiWfi) П dP，

(3.20)

B = 1

I,F

где суммирование проводится по всем каналам реакций (3.16). Полагая в (3.20) Wa = ga, г де ga — некоторые фундаментальные заряды, сохраняющиеся в реакциях (3.16), получим с учетом (3.15), (3.17) и (3.20) уравнения переноса плотностей потоков числа частиц плазмы:

▽ i J G = о,

(3.21)

где:

Тi _ V^ ^2s + ¹    / £( DA Di /  ^d3P

J G =工 о \з g a     f ^{( x} ， ^P)^P V-g "^.

V ^{(2П ) 3}      P ( x )               P+

(3.22)

—вектор плотности фундаментального тока, соответствующего зарядам д_а. В частности, закон сохранения (3.21) всегда имеет место для каждого сорта частиц b (ga = ^а ) при условии упругости их столкновений. Полагая в (3.20) W 。 = P^k, получим с учетом (2.15), (3.15) и (3.17) уравнения переноса энергии-импульса плазмы:

▽ * Tik - кФ = о,

(3.23)

где введена скалярная плотность заряда, ст, [5]:

σ

a

2S + 1 dm2

干

(2п)3 "Ф

Г       , 一 d³P

/ f (x,P )V-g ~^+,

P(x)                   P4

(3.24)

В частности, при выборе функции массы в виде (2.32) выражение для скалярной плотности зарядов

принимает вид;

ст = ^ф £ 2S+¹ q² / f ( x^,P)V-gdP. V ^{(2П ) 3}    P (x)             pJ

(3.25)

Следует отметить, что форма (ТЭИ) (3.5) или (3.13), а также скалярной плотности заряда (3.24), найденная для скалярно заряженных частиц в [4], при заданной функции Гамильтона является

однозначным следствием предположения о сохранении полного импульса в локальных столкно

вениях частиц. В частности, для системы, состоящей из односортных частиц, вследствие (3.6) и

(3.24) имеет место соотношение:

d ln m *

^ст = тт   Tp.

dФ   '

(3.26)

При выборе функции эффективной массы в виде (2.32) предыдущей работы это выражение упрощается и становится справедливым и для многокомпонентной системы:

Tp ф,

(3.27)

4. Локальное термодинамическое равновесие плазмы в гравитационном поле

4 ・ /. Локально равновесное распределение

В условиях термодинамического равновесия:

dS

dτ

(4.1)

Предположим сначала, что взаимодействие всех частиц Т - инвариантно. Тогда равенство (4.1) может выполняться лишь при выполнении условий (см. [13]):

Zfi - Zif =0

(4.2)

в каждом канале реакций (3.16). Уравнения (4.2) являются аналогом функциональных уравнений Больцмана [18]. Для их решения сделаем замену:

F_a = е ^{-ф а} ( е ^{-ф а} 干 1 )Т 三 ( 1 干 е ^{ф а} ) - 1,                            (4.3)

в результате которой величины Zif и Zf примут вид:

口 e - Фа             П е ^{-Ф а}

Z=iZ,=f

(4-4)

口 (e ^- 0^a 干 1) '          口 (е ^{-ф а} 干 1)

i,f                                 i,f

Тогда после логарифмирования уравнения (4.2) примут вид:

m VA            m ' ^V A

ЕЕ ф а (р а ) = Е Е ФВ 储 ) ,

A=1a=1          B=1в=1

причем, эти соотношения должны выполняться в каждом канале реакций (??). Единственным решением (4.5) при произвольных значениях импульсов частиц являются линейные функции импульсов:

'                                    Фа (PA) = -Aa(x) + (€a, PA),(丄 где вследствие инвариантности функции распределения: Аа(х) - скаляры в конфигурационном пространстве1. £i(x) - в(?кторы. Подставляя (丄6) в уравнения (丄5) ii учитывая закон сохранения обобщенного импульса при столкновениях, получим вследствие произвольности импульсов частиц:

EA (x)= gi(x);

N

Е VA人A = 0 ,(4-8)

A=1

где ||vA || - тіелочііслеішая матритіа. введенная в [13]. Вследствие очевидного условия замкну工ос工口 всех циклов реакций rank||vA|| < N(4.9)

уравнения (4.8) всегда имеют нетривиальное решение.

Условия (/.刀, (4 ・ 8) являются условиями локального термодинамического равновесия (ЛТР);

скаляры А а ( х ) называются хшшчестлш потенциалалш ст ， ат ， ист ， инеской система.

Подставляя решения (4.6) в (4.3) с учетом (4.7) получим локально - равновесные функции распределения:

f0(x, Pa) = { exp[-% + (е, Pa)] 干 1 } — 1 ,                          (丄 10)

где верхний знак, как и ранее, соответствует бозонам, нижний - фермионам.

Для сходимости моментов от распределения (4.10) необходима времениподобность вектора fi(x) ：

'                                              е² 三 (е,е ) > о.                                         (丄 п )

Введем с помощью £i(x) единичное времениподобное поле vi(x):

ξi vi =    ； (v,v) = 1,                                       (4-12)

локальную температуру Ө(х) [18]:

'              '                           Ө(х)= е-1                                              (4-13)

и химические потенциалы, 〃 a(x), в обычной нормировке:

Ma(x) = Ө(х)Аа (x).                                         (4.14)

Тогда распределение (4.10) может быть записано в виде:

f0(x, Pa) = { exp ^- 〃 ^a +J ^{P a )} 干 ‘ } ¹ .                       (4.15)

• 4.2.    Моменты равновесного распределения

Вычислим моменты распределения (4.10). При этом удобно перейти в локально лоренцевый репер, временная компонента которого направлена вдоль вектора vi и ввести новые переменные Pi = Pi - eA 心 в которых уравнение массовой поверхности (2.12) принимает вид ：

P4 = P² + m ： ,

(4.16)

(4.17)

где ：

m*(x) = |m + дФ(х)| является эффективной массой частиц. Затем необходимо перейти к сферической системе координат в пространстве импульсов P(X) и ковариаитио обобщить полученные результаты. В итоге получим выражения для компонент вектора плотности числа частиц, na(x), и ТЭИ a-той компоненты пла：змы. Tik [8]. [17]：

a где

na(x) = na(x)vi ；

Tik (x) = (Ea + Pa)ViVk — Pagik , a

Ea(x)

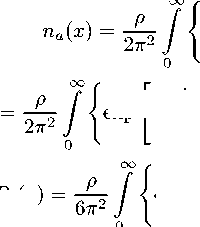
θ exp

Pa (x)

exp [

exp

-心 + ，時 + P²

“a + +P²

θ

干 1

“a + ， m 』 +P²

θ

}

]干 1} P2dP ；

-1

,m / + P²P²dP ;

∓

P4dP

В формулах (4.20) - (4.22) введены обозначения [8]:

《( с) = 〃 a(x) — ea(v, A).

(4.18)

(4.19)

(4.20)

(4.21)

(4.22)

(4.23)

Следует заметить, что химические потенциалы 〃 ： ^Б отличие от потенциалов 〃。 не сохраняются подобно (4.8) в реакциях, нарушающих закон сохранения векторного заряда. Для этих потенциалов вместо (4.8) получим:

' £ vA 溢 =- △ e^k(v,A). (4-24)

4 ・ 3. ЛТР при нарушении Т-инвариантности

Химический потенциал безмассовых частиц, обладающих нулевыми фундаментальными зарядами, в состоянии ЛТР равен нулю. Этот вывод следует из того, что числа vA таких частиц, участвующих в реакциях (4.8), могут быть совершенно произвольными. Тогда из факта существования реакции аннигиляции частиц и античастиц следует известное соотношение [19]:

必 a = -Ma . (丄 25)

Вследствие определения (4.23) это соотношение сохраняет силу и для перенормированных химических потенциалов 〃：• Аналогичные выводы можно сделать и в отношении фундаментальных зарядов gA： g a = -gA. (丄26)

Заметим, что единичный вектор в направлении вектора плотности потока числа частиц называется кинематической скоростью среды^ а собственный времениподобный единичный вектор ТЭИ частиц называется динамической скоростью среды^ собственное же значение ТЭИ, соответствующее этому вектору, называется плотностью энергии среды (см., например, [16]).

Таким образом в состоянии ЛТР кинематическая скорость частиц совпадает с их динамической скоростью и равна Vi. Плотность энергии частиц равна согласно (4.19)

E (x) = £ Ea ,

(4.27)

(4.28)

а изотропное давление всех сортов частиц:

P (x) = £ Pa , где1 Ea ii Pa- оппсыватотся (формулами (4.21) ii (4.22).

Рассмотрим теперь Т-неинвариантные взаимодействия, предполагая, однако, что распределение частиц остается локально равновесным, т.е., (4.10). Но тогда тождественно выполняются функциональные соотношения (4.2). Но тогда скорость изменения энтропии равна нулю, т.е., мы снова получаем условие ЛТР (4.1). Итак, энтропия системы всегда сохраняется, если распределение частиц является локально равновесным.

Обратимся теперь к уравнениям переноса (3.20). В условиях ЛТР вследствие (4.3) эти уравнения принимают более простую форму:

必 Zif (Wif - Wfi) П dn.

i,f

(4.29)

▽ i 2 / ^fp^ldn - £ / f [H ， 叫 dn = - 2 / S ⑷ (P f - P i ) 2 "A A p            A p                  k p               A

Полагая, в частности, “A = %, получим из (4.29):

Vina = - 2 vA / S ⑷ (P f - P i )Zif (Wif - Wfi) П dn.

(4.30)

Проведем в правой части (4.30) интегрирование по конечным состояниям частиц:

2 vA/ 屮

1 ± f )(Wif - Wfi)dnf .

Вследствие унитарности S-матрицы и оптической теоремы (см. [13]) этот интеграл равен нулю. Поэтому в условиях ЛТР имеет место закон сохранения каждого сорта частиц:

Vina = 0 О Na = Const .

(4.31)

5.    Глобальное термодинамическое равновесие

В случае, когда функции распределения (4.10) (или (4.15)) являются точными решениями кинетических уравнений, статистическая система находится в строгом глобальном термодинамическом равновесии (ГТР). В условиях ГТР выполняются строгие законы сохранения частиц каждого сорта (4.31), и энтропия системы строго постоянна S = Const. Для нахождения условий ГТР в случае Т-инвариантных взаимодействий, подставим решения (4.10) в кинетические уравнения. Поскольку интеграл Т-инвариантных взаимодействий обращается в нуль на локально равновесных распределениях, приведем кинетические уравнения к виду:

[На,Фа]=0 ,

(5.1)

где ：

0a (x, ^р) d= (g, ^p)— 人 a ^(x).

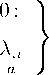
Таким образом, для обеспечения ГТР должен существовать линейный интеграл движения, причем gi - времениподобный вектор.

Разрешая (5.1), получим систему необходимых и достаточных условий существования ГТР [8],
[17]:
L gik = 1gik ； ξ		(5.2)
ma }ma + qa^)1 + ]a L@]	=0;	(5.3)
ea L Ai =A ,i. ξa		(5.4)
В случае. когда, ma 壬 0. получим из (52) ：
L gik (ma + ІоФ) = 0 ； ξ ea L Ai            = A ,i ξa	(ma 壬 0).	(5.5)

Для системы безмассовых частиц ma 三 0 эти условия заменяются следующими:

Если же в равновесии находится более одного сорта частиц, (5.5) заменяются более жесткими условиями [8]:

L gik     = 0 ； 1

L ^Ф = ⁰ ； 卜 ( ma 芒 0) .                             (37)

ea L Ai = 入 2 I

ξa

Вследствие условий на векторный потенциал, которые справедливы во всех случаях, выполняется закон сохранения модифицированного химического потенциала [8]:

L* ' =0 ；    (》' = 入— ea(^,A)).                                  (5.8)

Поскольку все моменты равновесной функции распределения определяются с помощью скаляров ^2. XL Ф 口 тензоров £< gik. gigk.....то вьшо/нятотся ii ^законы сохратіетшя мом(?итов (функции a распределения [8]:

L na =0；(5.9)

ξ

L Ji = 0;(5

ξ

LTik = 0(5.П)

ξa и т.д. В [21], [22] показано, что необходимым и достаточным условием интегрируемости уравнений (5.8) относительно X являются:

a

L Fij=0.                                    (5 」 2)

Для доказательства (5.12) достаточно вычислить вторые смешанные производные от обеих частей уравнения:

ea L Ai =X,i ξa и приравнять их. После коммутации производных Ли и ковариантных производных получим (5.12).

Вследствие первой группы уравнений (5.7) вдоль направления gi сохраняются компоненты тензора Римана, Риччи и тензора Эйнштейна:

L Rijki = 0 ; L Rj = 0; L Gij = 0 .                          (5.1,3)

Поэтому вследствие уравнений Эйнштейна должны выполняться соотношения:

L ”7=0.                                   (5 」 1)

6.    Глобальноетермодинамическое равновесие самогравитирующей системы со скалярным взаимодействием частиц

Этот случай был рассмотрен в [13,17]. Условия глобального равновесия принимают вид:

Xa = Const; L Ф = 0; L gik = 0 .                            (6.1)

Плотность энергии и давление плазмы определяются формулами (4.21) и (4.22), в которых следует положить ： Ai = 0- т.е.. определятотся двумя скалярами g(x) ii Ф(х). В целях обшпостп ігзложеііпя рассмотрим неконформно инвариантное скалярное поле.⁶ Вычисляя производную Ли от суммарного ТЭИ, получим:

^gigk L (E+P)⁺ g i^gk +1 ^kgi) E+P ⁺ 4П ( Ф ， ^iФ ， ^k + Ф ， ^kФ ， ⁱ)^—

^—gik [ l P⁺4s е” ф ，， — 〃 ^{2 ф}ф ) ]=^{0 ；}

(X = T~r ) ,

(6.2)

где:

①些 L Ф ； Ф d=L Ф ,і = di Ф; λ λ        λ_,i λ            λ

(6.3)

Es = ±1 (пятое ii минус соответствутот отталкііватошіімея ii прптягііватошішся барионам). В случае, если:

l P+. ej ф「〃2ффН 0， при каждом фиксированном А, то метрический тензор может быть выражен, как нетрудно убедиться, через три вектора, но в этом случае он вырожден (т.е., g = 0), чего не должно быть. Из (6.3) следует тогда, что должны выполняться 11r условий:

l P⁺4s ej Ф j - ^2^фф ) =^{o ；}

(6.4)

^{g i g k} L E+P ⁺ ( I i^{g k +} 1 ^{k g}i ) ⁺ 4s ( Ф ，浬,^{k +} Ф ，通) =^0; ( ^А = М •

Свертывая (6.5) с gigk и учитывая (6.1), получим:

L (E + P) = 0， а свертывая (6.5) с giФk, учитывая (6.1) и очевидное соотношение:

(( ,^Ф ) = ( ^g ， Ф ) , получим:

g 叫 E+P - 4s ( ^Ф ， 闸 =⁰.

Свертка (6.5) с Ф ^іФ^,к приводит к результату ：

(Ф, Ф)(Ф, Ф) = 0 . λ

Для решения (6.7) предположим сначала:

(g, Ф ) = 0.

λ

Тогда свертывая (6.5) с gk и учитывая очевидное соотношение:

L g2 =2(g,g),

(6.5)

(6.6)

(6.7)

(6.8)

(6.9)

найдем:

£一入

i 二 F L J

(6.10)

откуда получим:

L 3 = 0

и приведем уравнение (6.5) к виду:

ф ,іФ,к+ ф ,к Ф ,і = 0 .

В случае:

'                                                Ф,і = 0

единственным решением (6.12) является:

(6.11)

(6.12)

(6.13)

Тогда (6.4) сводится к соотношению:

L ( ^P -受叫=。 .

Рассмотрим другой вариант решения уравнения (6.7):

E + P - 4s (Ф ， Ф ) = 0 ；

(6.15)

(6.16)

тогда из (6.5) получим:

(Ф, Ф) = 0.

λ

Свертывая (6.5) с Ф ,k и учитывая (6.16) и (6.17), найдем:

(6.17)

(gik - vivk ) Ф ,k = 0 .

(6.18)

Используя (6.1), найдем из (6.18) Ф ,k = 0, т.е., снова приходим к (6.10), (6.11), (6.14) и (6.15).

Согласно (6.4), (6.5) скаляры E и P могут зависеть от координат лишь посредством функций £(x) ii Ф(х). Из уравнетшіі (6.6) ii (6.15) получим систему однородных алгебраических уравнешііі от носите лыю Ф 11 £

дй +為

Ф=0;

(6.19)

d(E + P) , , d(E + P) 亠 n д£ А ⁺   дФ   ⁺ .

В случае, если определитель этой системы отличен от нуля, получаем:

(6.20)

λλ

Но тогда из (6.6), (6.10), (6.12) и (6.22) следует:

L E = 0 ;

λ

Ф = L Ф = 0 ; λλ

£ 三 L£ = 0 .

(6.21)

(6.22)

L£ = 0;

L P = 0;

( 人 = 巧).

(6.23)

(6 ・ 24)

В случае же равенства нулю определителя системы (6.19) - (6.20) легко показать, что: Ф = Ф(£); E + P = Const .

Из (4.21), (4.22) вытекает, что это возможно лишь при £ = Const, но тогда и Ф = Const, т.е., вновь получаем условия (6.21) - (6.24). Достаточность же этих условий для сохранения суммарного ТЭИ при движении вдоль траекторий Gr проверяется элементарно.

Таким образом, и глобальное равновесие самогравитирующей статистической системы со скалярным взаимодействием частиц возможно лишь в том случае, когда пространство - время лопускает группу движений с времениподобным центром, вдоль которого происходит макроскопическое движение системы.

7. Макроскопические плотности

7./. Полностью е ырож.денный газ Ферми

При условии полного вырождения

， га. θ

(〃 - химический пот еішп ал. Ө - темпер атур а) /токасьно - р авиовеси а ， я (функция р аспределеипя Ф ер -ми - системы является ступенчатой функцией (см., например, [19]), которая для релятивистских скалярно заряженных фермионов принимает вид [6]:

f0 (x, P) = х+ ( 〃 一 7^m + Р²),                              ('"-2)

rje x+(z) - (функция Хевисайда ：

m * = m + дФ | ,

(7.3)

—эффективная масса фермионов, q - скалярный за ряд фермионов, Ф - потенциал скалярного поля, m - вакуумная масса (фермионов. В этом случае макроскопические плотности выражатотся в элементарных функциях [13]:

где

pf = 24П2     丄 + W²HW — 3 ) ⁺ 3in ( ^ +

Tf = % - 3pf = 2П2 [3 ， i + 3² - in@ +

£f + Pf = 3П * 2 也 3 ， ¹ + 呪 ；

° = ^ Tf = 1^2* [ 7^{1 +} [² - m 侬 + 、 m _∗       2n   L

3 = pf / | m * |

， 1 + 32) ] ;	(7.4)
7 1 + 32) ] ；	(7.5)
7 1 + 32) ] ；	(7.6)
	(7.7)
7 1 + 32) ] ；	(7.8)

(7.9)

—отношение импульса Ферми к эффективной массе, £f ,pf, ° - плотность энергии, давление и плотность скалярного заряда фермионов, соответственно⁷. В качестве уравнения скалярного поля рассмотрим уравнение массивного скалярного поля с массой бозонов 〃 [?] ：

□Ф + 〃 ²Ф = — 4п°.

(7.10)

Плотность числа фермионов, n, связана с импульсом Ферми соотношением [19]:

p3f                        1

n(x) = 7-^7 今 Pf = (3n²n(x))³.

3п2

(7.11)

Таким образом, переменную 3 можно выразить через два скаляра - плотность числа частиц в собственной системе отсчета, n(x), и скалярный потенциал, Ф(х):

(3n2n(x)) 3

3 — ~i       "7Л ~ .

| m + qФ |

(7.12)

7Подробности см. в [?].

8.    Самосогласованная система уравнений для плоской модели Фридмана

Рассмотрим космологическую ситуацию, когда материя представлена лишь вырожденной Ферми -системой скалярно взаимодействующих частиц и связанных с ними скалярным полем, описываемых уравнением (7.10) (см. [5]). В качестве метрики выберем метрику пространственно-плоской модели Фридмана [14]):

ds2 = dt2 - a2(t)(dx2 + dy2 + dz2),

(8.1)

(8 ・ 2)

(8.3)

в которой независимые уравнения Эйнштейна имеют форму:

а2

3— = 8 п£ ； a²

a u ° a u + P.

В этой метрике закон сохранения числа частиц принимает форму8:

dt V—gn = 0, откуда с учетом (7.11) получим интеграл импульса [5]:

арғ = Со nst.

(8.4)

Полагая далее Ф = Ф«) получим u = u(t) р = p(t) ii структуру теігзора энергии - импульса скалярного поля в форме тензора энергии-импульса идеальной жидкости с макроскопической скоростью vi = б ； ii плотпостыс) эіі ( ?ргіш Us(t) ii давя синем Ps(t) ：

Us = ?(Ф 2 + 〃 2Ф2) ； Ps =^(1Ф 2 — 〃 2Ф2) ・ 8n                    8n 3

(8.5)

Дифференцируя (8.5) и подставляя результат в (8.3), можно убедиться в том, что полученное уравнение является следствием уравнения поля (7.10), которое в метрике (8.1) принимает вид:

丄 _£ 3 雪   ²_ф = _₄

(8-6)

a³ dt ( a dt ⁾⁺ 〃 ^Ф

Таким образом, в качестве независимых уравнений можно выбрать уравнение поля (8.6) и первое из уравнений Эйнштейна (8.2), которое с учетом положительности скорости расширения (а > 0)

запишем в виде:

a

a

/ 8n

V тu,

(8 ・ 7)

где

U = Uf + Us

-суммарная плотность энергии фермионов и скалярного поля.

Проведем анализ возможного космологического поведения системы вырожденных скалярно заряженных фермионов. Из выражений для макроскопических плотностей (7.4), (7.5) можно получить соотношение:

Pf = 3^uf — 2mn2 |4.,1 + >2 — ³ln@ + ,1 + 呪 )].                  (8-8)

Можно показать, что выражение в квадратных скобках правой части (8.8) неотрицательно при неотрицательных > > 0. Поэтому выполняется строгое неравенство:

(8-9)

0 < Pf < 1 uf.

Аналогично из (8.5) найдем соотношение для скалярного поля:

ps

3 ^us ^-白沙

(8.10)

'Всюду G = 方 =c = 1・ время ii :масс 。 измеряются в ппанковскик едшпш.ах.

Таким образом и для скалярного поля выполняется строгое неравенство:

(8.11)

Ps 工 з £ s ・

Вычислим теперь коэффициент баротропы, как коэффициент к в линейном соотношении между суммарным давлением и плотностью энергии материи:

В результате найдем:

где:

P = К£.

—1   m4G( ^ ) + 4п 〃 2Ф2

K(t) = 3      24n2(fs + £f)   ,

G ⑹ =4 別 ， 1 + 32 — 3 ln@ + д/1 + = 2) .

(8.12)

(8.13)

Таким образом, можно показать, что для исследуемой системы всегда выполняется соотношение:

今- 1 <  K ( t) <  3.

(8.14)

Таким образом, для космологического ускорения, ®, Вселенной, состоящей из вырожденных фермионов и скалярного поля,

® = aa = — I ^{( 1} +^{3к ) ,}                                ( 815 )

a2     2

получим ограничение:

— 1 <  s <  1.

(8.16)

9.    Численное решение уравнений Эйнштейна для вырожденной плазмы со скалярным полем

Попытки прямого численного интегрирования системы уравнений Эйнштейна - Клейна - Гордона (8.2), (7.10) в большинстве случаев не дают результатов вследствие нелинейного характера этих уравнений и неоднозначности функций радикалов и логарифмов в правых частях уравнений. Поэтому для численного решения системы уравнений Эйнштейна выражения для макроскопических плотностей были экстраполированы с помощью элементарных аналитических функций. Как видно из (7.4)-(7.8), все эти выражения с учетом интеграла (8.4) с точностью до умножения на конформный множитель 1/a4 являются элементарными функциями лишь одной безразмерной функции =： m4 =(嘆 У                       (9.1)

∗ _aψ

Это факт позволяет найти интерполяционные выражения для соответствующих конформных плотностей:

pf = a"Pf ; Sf = a⁴£f ； 5 = a⁴ a.                               (9.2)

Интерполяционные аналитические функции для плотности энергии, давления и плотности зарядов на всем исследуемом диапазоне можно записать в виде:

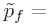
_8 e-2 吵 15

=+

2=2

3(1+ =2)

(9.3)

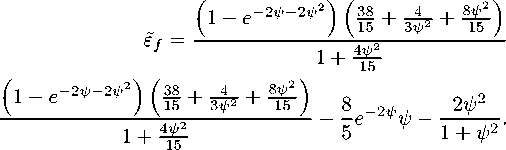
(9-4)

(9.5)

Очевидно, что вследствие большого количества существенных метра 、 pf,m, 〃， q[ ii начальных условий. (2 незашісіімнх условия.

параметров модели, (4 пара да 主 \

Ф(0), Ф(0)Ь рас см анриваемая

космологическая модель чрезвычайно богата типами поведения. Рассмотрим поэтому основные из них. Ниже приведены результаты численных решений полученных уравнений Эйнштейна - Клейна -Гордона для вырожденной Ферми-системы в прикладном математическом пакете Mathematica. v7.

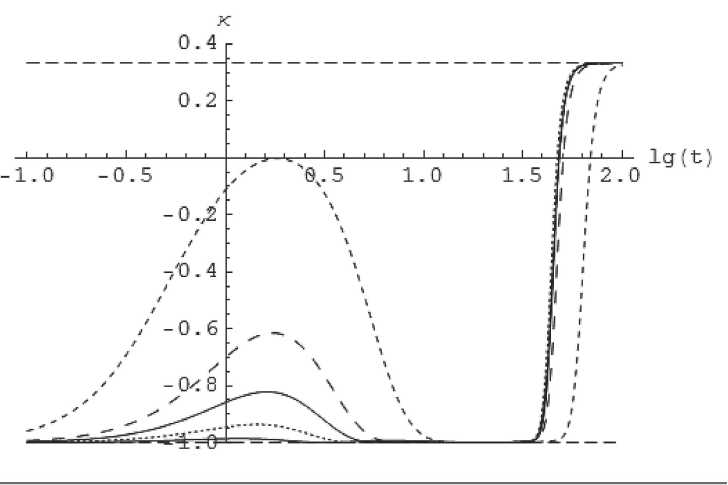
Рис. 1. Эволюция коэффициента баротропы в зависимости от массы скалярного поля. Частая пунктирная линия: 〃 = 0 , 3; пунктирыая линия: 〃 = 0 , 1; разреженная пунктирная линия - 从 =0 , 2; сплошиая линия: 从 =0 , 25; сплошная ж ирная линия: 从 =0 , 35. Всюду: PF = 0, 01; m = 1; q = 0, 3;Ф(0) = 1; Ф(0) = 0.

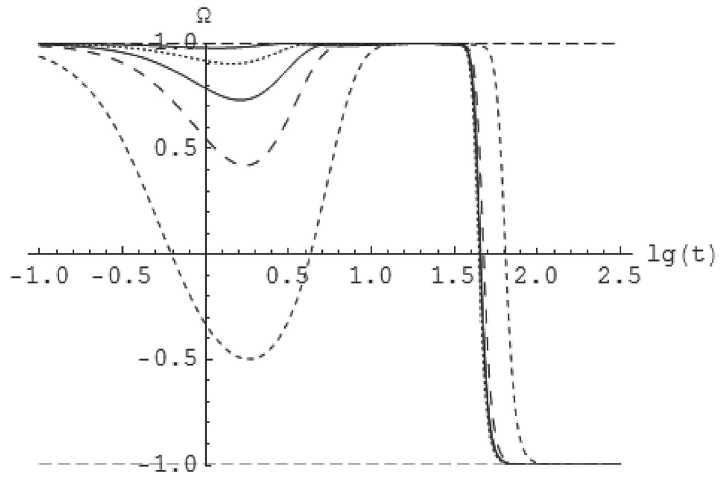
Рис. 2. Эволюция космологического ускорения в зависимости от массы скалярного поля. Частая пунктирная линия: 从 =0 , 3; пунктирыая линия: 从 =0 , 1; разреженная пунктирная линия - 从 =0 , 2; сплошиая линия: 从 =0 , 25; сплошная ж ирная линия: 从 =0 , 35. Всюду: P f = 0, 01; m = 1; q = 0, 3; Ф(0) = 1; Ф(0) = 0.

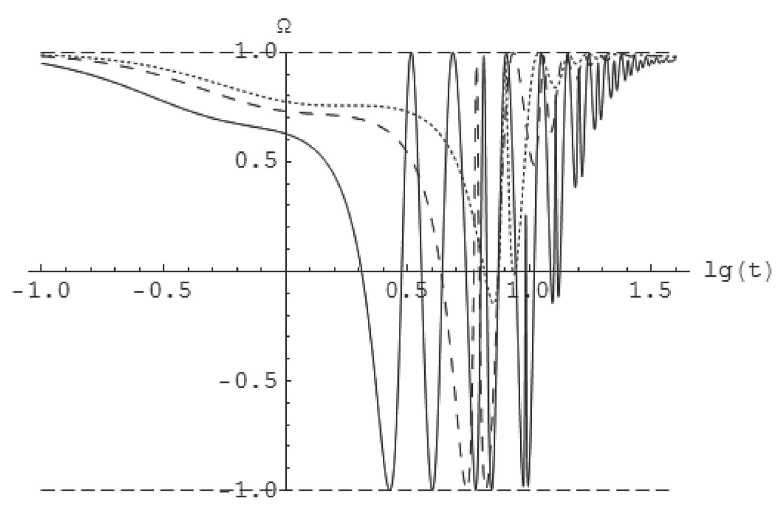
Рис. 3. Эволюция космологического ускорения в зависимости от массы скалярного поля.

Частая пунктирная линия: 儿 =1; пунктирыая линия: 儿 =1 , 2; сплошная линия: q = 2; сплошная жирная линия: q = 0, 35. Всюду: pF = 0, 01; m = 1; q = 0, 3; Ф(0) = 1; Ф(0) = 0.

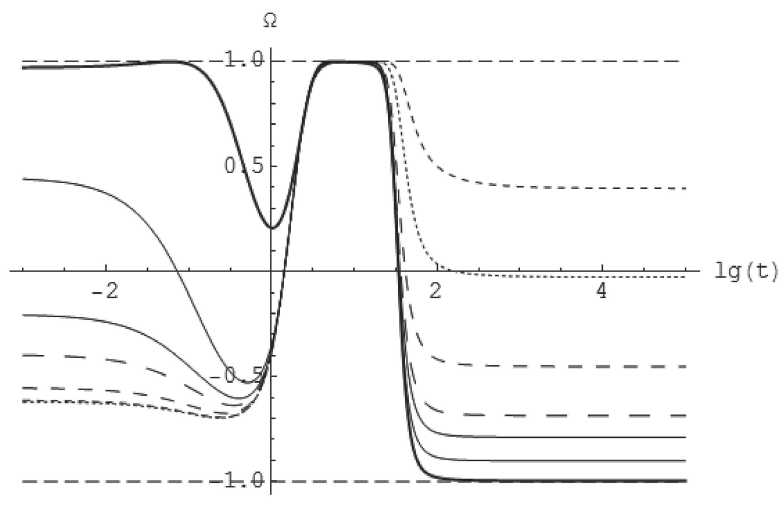
Рис. 4. Эволюция космологического ускорения в зависимости от массы фермионов. Частая пунктирная линия: m = 0, пунктирыая линия: m = 0, 001, разреженная пунктирная линия: m = 0, 01, eine более разреженная пунктирная линия: m = 0.03, сплошная тонкая линия: m = 0, 05, сплошнаялиния: m = 0,1, сплошная ж ирная линия: m = 1. Всюду:

P f = 0, 01; q = 0, 3; q =1;Ф(0) = 1; Ф(0) = 0.

Приведем решения, которые переходят на ускоренную космологическую фазу с максимальным ускорением. Эти решения соответствуют весьма малым значениям фундаментального заряда.

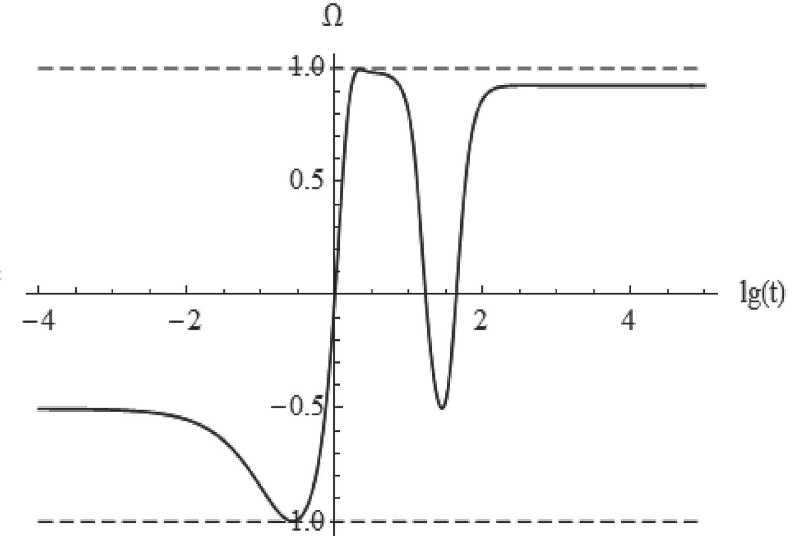
Рис. 5. Эволюция космологического ускорения, ш при рғ = 0; m = 1; 从 =0 , 001; q т 0.

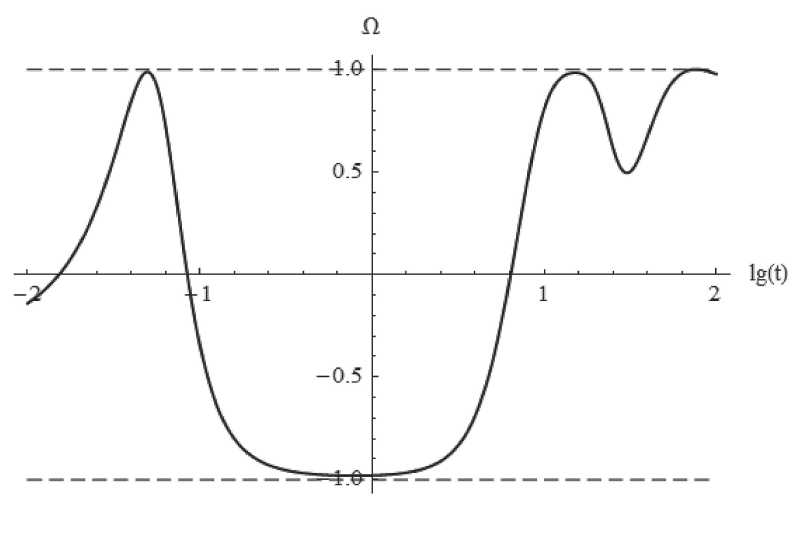
Рис. 6. Эволюция космологического ускорения, ш, при рғ = 0; m = 1; 〃 = 0,1; q т 0.

10.    Выводы

Таким образом, можно констатировать, что:

• •    Поведение космологической модели чрезвычайно сильно зависит от фундаментальных констант q, ^ и m и весьма богато разнообразием типов;

• •    Сутцествуют области фундаментальных констант и начальных условий, в которых космологические модели выходят на устойчивое позднее ускорение;

• •    Выход на стадию позднего ускорения может быть как плавным, так и сопровождаться колебаниями ускорения;

• •    Конечное ускорение постоянно и может меняться в диапазоне —1 < % < 1.

Таким образом, постоянное ускорение (замедление) носит общий характер.

Автор благодарен профессорам В.Н. Мельникову, Д.В. Гальцову и А.А. Грибу за полезное обсуждение работы.