Неосесимметричная математическая модель анатомии левого желудочка сердца
Автор: Правдин С.Ф.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 4 (62) т.17, 2013 года.
Бесплатный доступ
Приведена математическая модель, описывающая форму и поле направлений мышечных волокон в левом желудочке сердца. Желудочек составлен из поверхностей, моделирующих мышечные слои, с построенными на них кривыми – мышечными волокнами. Касательные к этим кривым формируют поле направлений волокон. Волокна построены как образы хорд некоторого полукруга, параллельных его диаметру. Для задания формы левого желудочка использована специальная система координат, в ней границы желудочка являются координатными поверхностями. Предложено аналитически заданное отображение точек полукруга в точки в специальной системе координат. Модель соотнесена с концепцией единой миокардиальной ленты Торрента-Гуаспа и с идеей вложенных поверхностей Петтигрю. По экспериментальным данным диффузионно-тензорной магнитно-резонансной томографии были построены модели двух конкретных левых желудочков: здоровой собаки и здорового взрослого человека. Исходными данными для моделей послужили лишь сведения о форме стенок желудочков. В локальной системе координат, связанной с меридиональным сечением желудочка, были вычислены два угла наклона волокон: угол истинного наклона волокна и винтовой угол. Эти же углы были найдены из данных диффузионно-тензорной магнитно-резонансной томографии, было проведено их сравнение с модельными углами. Приведены графики этих углов и показано, что модель адекватно воспроизвела ход волокон в большинстве участков стенки желудочка. На основе предложенной математической модели можно построить вычислительную сетку, которая позволит решать задачи расчета электрофизиологической и механической активности левого желудочка в норме и при патологии. В вышеупомянутой специальной системе координат соответствующая численная схема будет записана в прямоугольной области, а граничные условия будут записываться особенно просто. Изменением параметров модели легко можно задать общее или региональное утолщение стенки желудочка, а также изменение его формы, например на более сферическую, что характерно для некоторых заболеваний сердца.
Левый желудочек, архитектоника миокарда, мышечные слои, математическая анатомия, аналитическая модель сердца
Короткий адрес: https://sciup.org/146216119
IDR: 146216119 | УДК: 51-76,
Текст научной статьи Неосесимметричная математическая модель анатомии левого желудочка сердца
Современные модели таких сложных физиологических систем, как сердце, включают в себя описание происходящих в нем процессов от уровня молекул до уровня целого органа и позволяют изучать как механическую, так и электрическую активность сердца в норме и при патологии.
За последние несколько лет был предложен целый ряд моделей, описывающих электрическую и/или механическую функцию целого сердца или его отдельных камер [6, 11, 12, 17, 19, 22, 24, 28, 32, 35, 37, 38]. Для самых современных моделей детальное описание анатомии сердца и поля ориентации волокон в нем очень важны для корректного представления главнейших физиологических особенностей работы сердца.
Все подходы к представлению анатомии и анизотропии сердца могут быть несколько условно разделены на две большие группы: подходы, основанные на картировании индивидуальных сердец (в этом случае анатомической основой модели служат результаты измерения ориентации волокон в конкретном сердце, полученные с помощью разнообразных экспериментальных методов); и теоретические подходы, в которых поле ориентации волокон вычисляется по некоторым алгоритмам.
В 1972 году Торрент-Гуасп ( Torrent-Guasp ) выдвинул концепцию, представляющую миокард двух желудочков сердца как единую мышечную ленту, скрученную и завернутую в двойную винтовую спираль [33]. В статье [27] была предложена теоретическая модель анатомии и поля ориентации волокон в левом желудочке сердца, основанная на этой концепции. Эта модель базируется также на идее Петтигрю ( Pettigrew ) [26] о конструировании модели миокарда левого желудочка из вложенных поверхностей (мышечных слоев), заполненных кривыми (мышечными волокнами). Каждая из данных поверхностей, по Петтригрю, может быть развернута на плоскость в виде полукруга, а кривые на них при разворачивании становятся горизонтальными хордами этого полукруга.
Для верификации построенной модели в работе [27] были использованы экспериментальные данные Стритера ( Streeter ) [31] и Хантера ( Hunter et al. ) [23], было показано, что модель воспроизводит такие свойства анизотропии сердца, как вращение волокон в стенке левого желудочка, зависимость этого вращения от положения в стенке (основание или верхушка), спиральный ход волокон на верхушке и максимальный угол вращения волокон вокруг оси левого желудочка. Количественное сравнение с данными из указанных работ показало хорошее согласие модельных данных с экспериментальными.
В статье [27] описана осесимметричная модель усеченного (только ниже экватора) левого желудочка. Настоящая статья посвящена обобщению этой математической модели. Форма реального левого желудочка разных животных и человека может быть как достаточно близкой к телу вращения, так и существенно неосесимметричной. Например, левый желудочек собаки можно условно поделить на две части: выпуклую свободную стенку и значительно вдающуюся в верхнюю часть его полости межжелудочковую перегородку. Мы отказываемся от осевой симметрии, сохраняем понятие оси желудочка и строим неосесимметричную модель формы левого желудочка и хода волокон в его миокарде. В нашей модели как анатомия, так и поле направлений волокон определены аналитически.
Построение модели левого желудочка
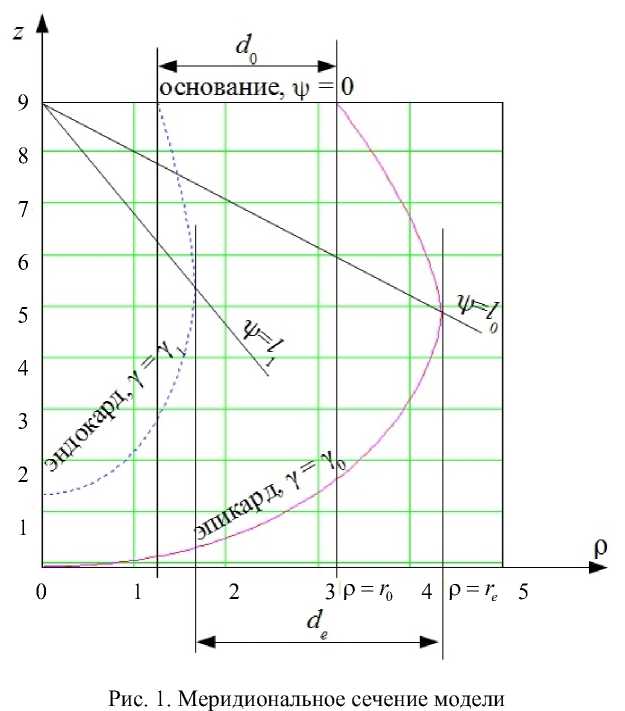
Для задания формы левого желудочка была использована специальная система координат (y, V, ф), где переменная Y е[у0, у1 ] с [0,1] соответствует положению точки в толще стенки левого желудочка, у = у0 - эпикард, у = у1 - эндокард; Vе [0; п/2] - аналог географической широты, ψ = 0 – самая верхняя плоская часть модельного левого желудочка (зона клапанов и фиброзного кольца), ψ = π/2 – верхушка левого желудочка; фе [0; 2п) - аналог географической долготы.
Переход от специальных координат к цилиндрическим (ρ, φ, z) осуществляется согласно следующим формулам (рис. 1):
р(у, V, ф) = р/втег (у, r0f (ф)-Ydo (ф) , ref (ф)-Ydf (ф) , /1f (ф) + y(l0 (ф)-l{ (ф)), p(ф)), z(у, у) = Zf —(Zf — hfy)sinу + Az,
|
( 1 ) 1 r e "/ r e р inmer (V , r 0 , r e , 1 , P М r • 1 - e L |
- r 0 ) ^ ( 1 - Г у- / ^ |
у /1 ) P , если у< / , p 1 , если у > / , |
|
чя/ 2 - / ^ |
где р inmer ( у , r 0, re , / , P ) — координата р точки с координатой у в стенке левого желудочка, если основание имеет координаты р = r 0, у = 0, экватор - координаты р = re , у = 0, а p > 1; r 0 e ( ф ) - радиус левого желудочка на эпикарде основания, экватора; d0e ( ф ) - толщина стенки левого желудочка на эпикарде основания, экватора; / 01 ( ф ) - «широта» у экватора на эпикарде, эндокарде; Z - высота левого желудочка; h – толщина стенки левого желудочка на верхушке; p (φ) > 1; индекс f означает формальный параметр, а r – реальный;
r of = r 0 r + d O r Y 0/( Y i -Y 0 ) , d o = d o r /( Y i -Y 0 ) , ^ = r er + d e Y 0/( Y i -Y 0 ) , d e = d r /( Y i - Y 0 ) , l 0 = [ ( Y i - 1 ) l i + ( 1 - Y 0 ) l 0 ]/ ( Y i - Y 0 ) , l i f = ( Y i l i r - Y 0 l 0 )/ ( Y i - Y 0 ) , h = h r/ ( Y i -Y 0 ) , Z = Z r + h r/ ( Y i -Y 0 ) , ^z = - h r Y 0/( Y i -Y 0 ) •
Спиральные поверхности
Миокард левого желудочка в модели состоит из волокон, лежащих на спиральных поверхностях. Уравнение спиральной поверхности в специальных координатах
ф ( У , Ф min, ф тах ) = ф тт + YФ max,
где ф тах - угол закрутки спиральной поверхности (одинаков для всех спиральных поверхностей), ф тax =ф max /(y i —Y 0 ) , разные спиральные поверхности отвечают разным значениям ф min е [ 0,2 л ) .
Уравнение спиральной поверхности в цилиндрических координатах (см. (1), (2)):
|
. Гф-ф . ) Р sp ( v , ф , Ф min ) = р Ф min , V , Ф , (5) V ф тах / z sp ( V , ф , Ф min ) = z ф Ф min , V . (6) V ф max / |
Построение волокон на спиральных поверхностях
Следуя теоретическому предположению Дж. Петтигрю [26] и его практической реализации [1, 2, 27], мы смоделировали волокна миокарда как образы хорд Y = const; Y е [0; i) полуокружности P = i; Ф е [0; п] параллельных ее диаметру, на спиральной поверхности (рис. 2). Каждую отдельную хорду мы параметризовали с помощью полярного угла Фе [ Ф 0, Ф 1 ] , где Ф 0 = arcsin Y , Ф 1 =п- arcsin Y . Отображение точки ( P ; Ф) на хорде в точку на спиральной поверхности задано формулами (рис. 3)
Ф
Y(Ф)= , п
Ф( Р ) = (i — Р)~-
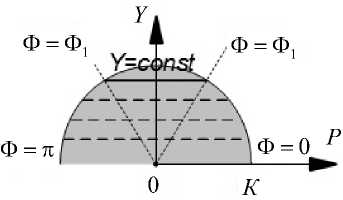
Рис. 2. Горизонтальные хорды на полукруге:
Ф 0 и Ф 1 - полярные углы соответственно
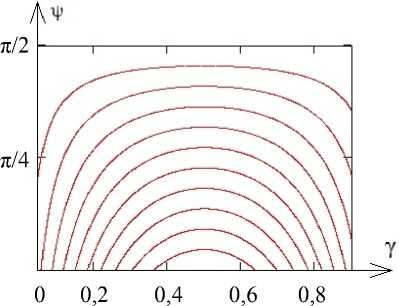
Рис. 3. Образы хорд полукруга в координатах ( y , v )
правого и левого концов хорды
Таким образом, образ диаметра полукруга – это волокно, начинающееся на эпикарде, спускающееся вниз до верхушки (Ф = π/2), а затем поднимающееся и заканчивающееся на эндокарде. Образы более коротких хорд находятся ближе к верху левого желудочка и имеют меньшую длину.
Приближение формы левого желудочка
Мы провели подгонку формы модельного левого желудочка к форме одного реального левого желудочка сердец собаки и человека на основе данных диффузионнотензорной магнитно-резонансной томографии, свободно доступных в Интернете по адресу: http://gforge.icm.jhu.edu/gf/project/dtmri_data_sets/docman .
Сначала мы построили ось Oz левого желудочка, затем рассекли его N = 20 (для собаки) или N = 24 (для человека) меридиональными полуплоскостями ф i = 2 п i/ N , i = 0, 1, …, N – 1, проходящими через эту ось, и вручную нашли значения необходимых параметров r 0, re , d 0, de , l 0, l 1, p в каждом сечении (рис. 4, 5). После этого с помощью кусочно-линейной интерполяции были найдены функции r0 ( ф ) , r e ( ф ) , d 0 ( ф ) , d e ( ф ) , 1 о ( ф ) , l i ( ф ) , Р ( Ф).
Методика сравнения модели и данных эксперимента
Сопоставление теоретической модели с данными эксперимента было проведено путем сравнения углов наклона волокон, пересекающих нормали к меридиональному сечению эпикарда, по методике, изложенной в работе [31] и заключающейся в следующем.
Для сравнения углов вдоль одной нормали нужно задать какую-либо точку A на эпикарде, пусть ее специальные координаты Ф = Ф 0 и ф = ф 0. Рассмотрим соответствующее меридиональное сечение ф = ф 0 модели - полуплоскость П. Построим нормаль к сечению эпикарда данной полуплоскостью и найдем ее пересечение с эндокардом или основанием – точку B . На построенном отрезке AB отметим к равноудаленных точек, включая его концы - A = A 1 , A 2, . . , Ak = B. Положение точки A i на отрезке AB отражает величина t4 = AB]AB (для эндокарда t = 0, для эпикарда t = 1).
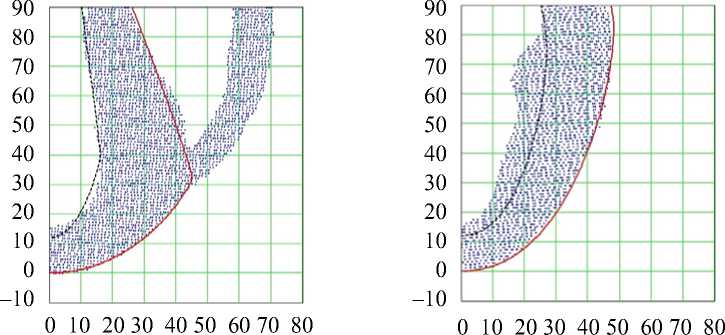
Рис. 4. Вертикальные (меридиональные) сечения межжелудочковой перегородки (слева) и свободной стенки левого желудочка (справа) сердца собаки. Точки – данные диффузионно-тензорной магнитно-резонансной томографии, сплошная кривая – эпикард модели, пунктирная кривая – эндокард модели. На рисунке слева полость левого желудочка левее, а полость и свободная стенка правого желудочка правее перегородки

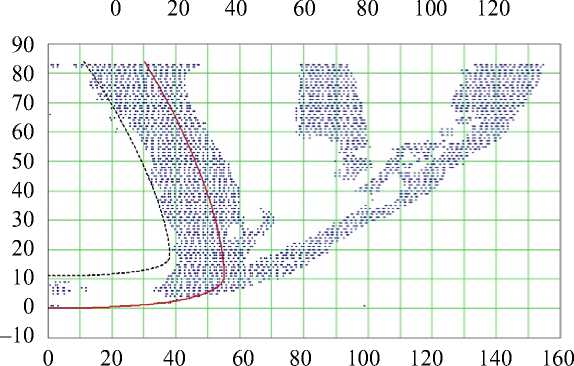
Рис. 5. Вертикальные (меридиональные) сечения свободной стенки левого желудочка (сверху) и межжелудочковая перегородка (снизу) сердца человека. Точки – данные диффузионно-тензорной магнитно-резонансной томографии, сплошная кривая – эпикард модели, пунктирная кривая – эндокард модели. Снизу в сечение попала папиллярная мышца в полости правого желудочка (вертикальная, ρ = 80...100 мм) и его свободная стенка (наклонная)
Через каждую из точек Ai нам пришлось провести спиральные поверхности. Задача нахождения такой спиральной поверхности сводится к решению системы двух уравнений с двумя неизвестными у и ф min:
Рsp (V, Фо, Фтт ) = Рi, zsp (V, Фо, Фтт ) = zi, где (рi, ф0, zi) - цилиндрические координаты точки Ai.
Эта задача эквивалентна переводу цилиндрических координат точки в специальные, т.е. решению системы
p(y, V, Фо ) = Рi, _z(у, v) = zi относительно ψ и γ. Из второго уравнения этой системы можно выразить ψ:
v ( z i , y ) =
arcsin
Л Z- f - z i + A z Л
V Zf - hf Y v
и подставить это выражение в первое уравнение. Тогда задача сведется к решению одного нелинейного уравнения вида
р(у, ф(zt, у), Фо) = pt с одним неизвестным у на отрезке [у0, у1 ], что может быть легко сделано, например, методом касательных.
Строго говоря, точно в полуплоскости П может вообще не оказаться точек из томограммы, поэтому мы отбирали точки, расположенные не далее Δ = 1 мм от прямой AB и внутри двугранного угла |ф - ф 01 < Аф = 0,1 рад = 5,7 ° .
В работе [31] Стритер предложил использовать для описания направления волокна локальную систему координат ( u , v , w ) и углы а «истинного наклона волокна» и а 1 «винтовой» (этих углов достаточно для задания направления волокна в точке). Ось u – это нормаль к эпикарду, направленная от левого желудочка; w – меридиан, т.е. касательная к эпикарду, лежащая в меридиональной полуплоскости и направленная вверх; v - параллель, то есть вектор w х u . Угол а е [0; п/2] - это угол между волокном и параллелью, а угол а 1 е [ -л/ 2, п/2 ] - между проекцией волокна на плоскость uv и параллелью.
Мы сравнили эти две угловые характеристики нашего поля направлений с данными эксперимента. Сравнение проводили вдоль нормалей к эпикарду в двух меридианах (один меридиан соответствует свободной стенке левого желудочка, другой – межжелудочковой перегородке) в верхней, средней и нижней частях стенки желудочка.
Результаты сопоставления с данными о сердце собаки
Мы использовали следующие значения параметров: высота левого желудочка Zr = 90 мм, толщина стенки левого желудочка на верхушке hr = 12 мм, эффективный угол закрутки спиральной поверхности ф max = 3 п , параметр субэпикардиального отслаивания у 0 = 0,05, параметр субэндокардиального отслаивания у 1 = 0,98.
На рис. 6 изображена построенная нами спиральная поверхность при указанных значениях параметров и образы хорд на ней.
Сравнение было проведено в разных зонах левого желудочка: верхней (нормаль к эпикарду построена в точке с координатой ψ = 5°), средней (ψ = 35°) и нижней (ψ = 65°).
На рис. 7–12 изображены области сердца, в которых мы сравнивали углы наклона волокон, и графики этих углов по данным эксперимента (точки) и модели (сплошные линии). Проанализируем каждый из этих шести рисунков подробнее.
В верхней части свободной стенки левого желудочка (см. рис. 7) мы наблюдаем качественное и хорошее количественное согласие данных: угол а максимален на эндокарде, убывает приблизительно до 10° в середине толщины стенки и затем
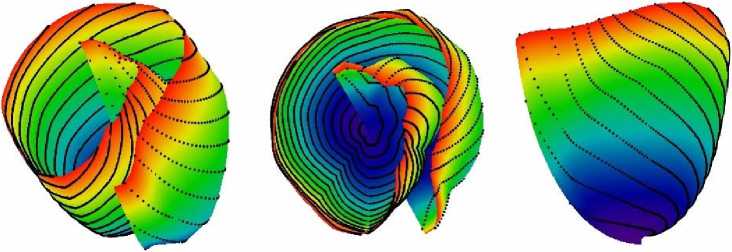
Рис. 6. Спиральная поверхность, используемая в модели левого желудочка человека, с образами хорд на ней. Слева – вид сбоку и сверху, в центре – вид сверху, справа – вид сбоку и чуть снизу

а
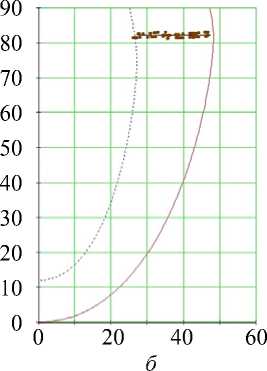
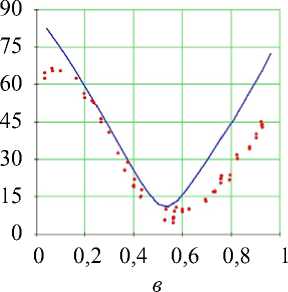
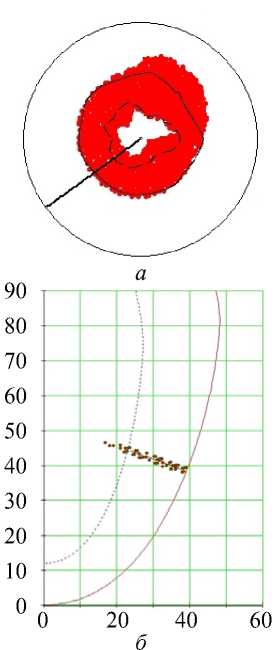
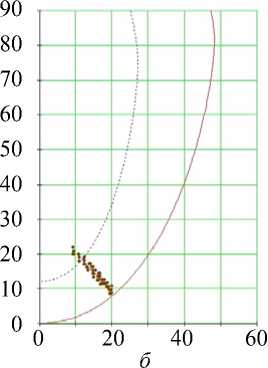
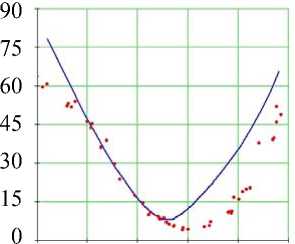
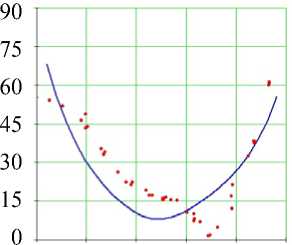
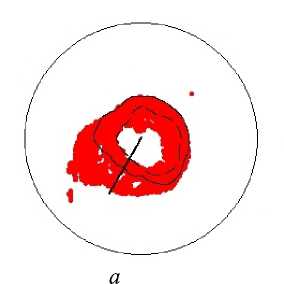
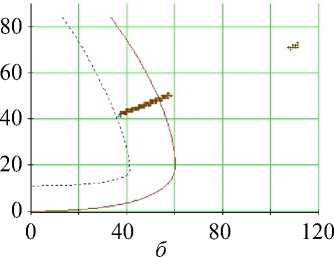
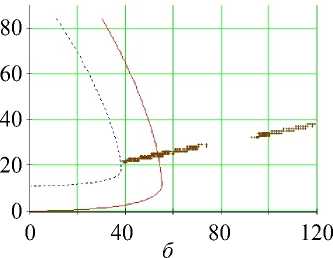
Рис. 7. Углы наклона волокон в модели и по данным эксперимента. Свободная стенка левого желудочка, область основания (ψ = 5°), собака: а – горизонтальное сечение левого желудочка, точки – точки миокарда из томограммы, сплошная линия – нормаль к эпикарду, сплошная (пунктирная) кривая – эпикард (эндокард) в модели; б – меридиональное сечение левого желудочка, сплошная линия – эпикард, пунктирная линия – эндокард, точки – точки миокарда из томограммы; в , г – углы α , α 1. Ось абсцисс – положение точки в толще стенки желудочка, 0 соответствует эндокарду, 1 – эпикарду
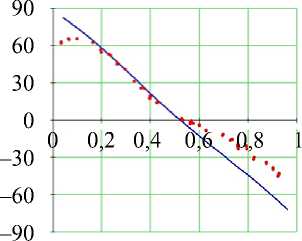
возрастает, достигая локального максимума на эпикарде. На рис. 7, г винтовой угол α 1 , если двигаться от эндокарда к эпикарду, почти линейно убывает от больших положительных значений до больших по модулю отрицательных и равен нулю в середине стенки.
Близкое поведение изучаемых углов мы видим и в средней по высоте части свободной стенки левого желудочка (см. рис. 8). По сравнению с предыдущим рисунком и в эксперименте, и в модели мы можем отметить следующее: графики угла α в области основания имели форму ближе к латинской букве V , а в средней области их форма стала ближе к латинской букве U ; график угла α 1 на рис. 7 был схож с прямой, а на рис. 8 стал чуть ближе к перевернутой кубической параболе (т.е. в середине стенки убывание этого угла замедляется, а в наружной и внутренней трети стенки ускоряется).
В зоне верхушки (см. рис. 9) количественное согласие данных становится хуже, но качественное воспроизведение сохраняется. Отметим, что график угла α 1 как в модели, так и в эксперименте стал еще ближе к перевернутой кубической параболе.
Рассмотрим теперь межжелудочковую перегородку и вновь сравним углы наклона волокон вдоль трех нормалей к эпикарду.
В зонах основания (см. рис. 10), средней (см. рис. 11) и нижней (см. рис. 12) наблюдается теперь лишь качественное согласие данных. Как и в свободной стенке, угол α истинного наклона волокон максимален на эндокарде, затем убывает, достигая минимума в середине толщи стенки, и возрастает, достигая максимума на эпикарде.
0 0,2 0,4 0,6 0,8 1
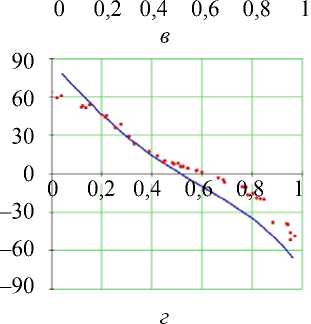
Рис. 8. Углы наклона волокон в модели и по данным эксперимента. Свободная стенка левого желудочка, средняя по высоте область (ψ = 35°), собака. Обозначения как на рис. 7
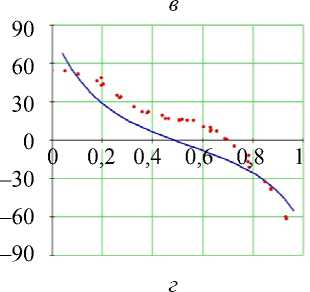
Рис. 9. Углы наклона волокон в модели и по данным эксперимента. Свободная стенка левого желудочка, область верхушки (ψ = 65°), собака. Обозначения как на рис. 7. Горизонтальное сечение ( а ) не приводится
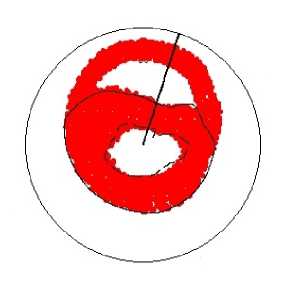
а
0 0,2 0,4 0,6 0,8 1
в
0 0,2 0,4 0,6 0,8 1
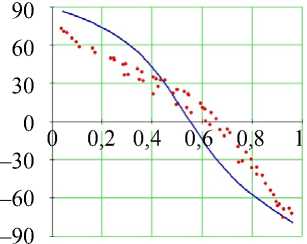
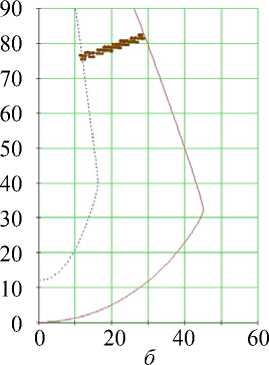
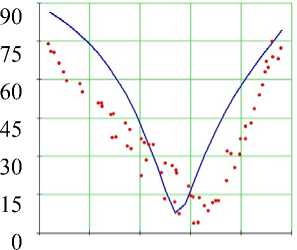
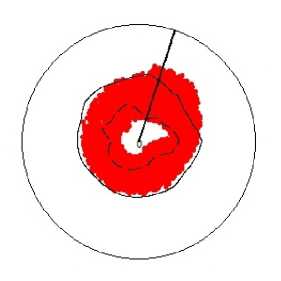
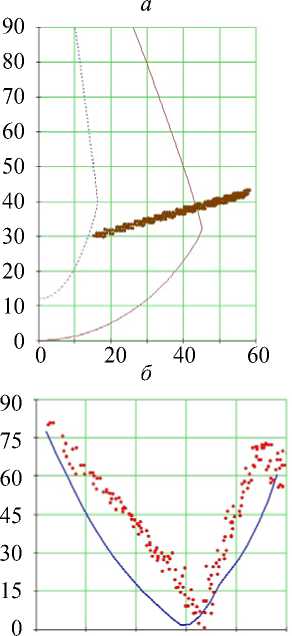
Рис. 10. Углы наклона волокон в модели и по данным эксперимента. Межжелудочковая перегородка, область основания (ψ = 5°), собака. Обозначения как на рис. 7
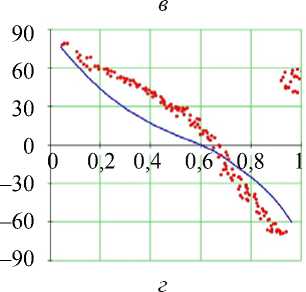
Рис. 11. Углы наклона волокон в модели и по данным эксперимента. Межжелудочковая перегородка, средняя по высоте область (ψ = 35°), собака.
Обозначения как на рис. 7
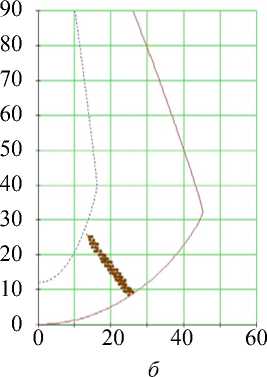
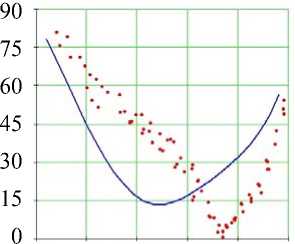
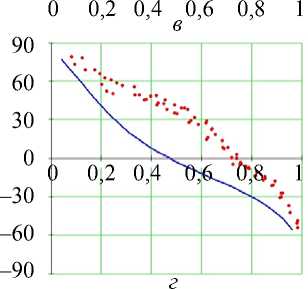
Рис. 12. Углы наклона волокон в модели и по данным эксперимента.
Межжелудочковая перегородка, область верхушки (ψ = 65°), собака. Обозначения как на рис. 7. Горизонтальное сечение ( а ) не приводится
Нужно отметить, что в эксперименте и в модели в средней и – особенно четко – в нижней части межжелудочковой перегородки эндокардиальное значение этого угла больше эпикардиального.
Винтовой угол а 1 в межжелудочковой перегородке монотонно убывает, как и в свободной стенке, от приблизительно 80° на эндокарде до примерно - 60 ° на эпикарде.
Результаты сопоставления с данными о сердце человека
Методика сравнения углов наклона волокон была той же, что и для случая сердца собаки.
Не зависящие от меридиана параметры модели сердца человека: высота левого желудочка Zr = 84 мм, толщина стенки левого желудочка на верхушке h r = 11 мм, эффективный угол закрутки спиральной поверхности ф max = 2 п , параметр субэпикардиального отслаивания у 0 = 0,05, параметр субэндокардиального отслаивания у 1 = 0,98.
Графики зависимости углов а , а 1 от положения точки на нормали к эпикарду в стенке левого желудочка приведены на рис. 13–18. Проанализируем полученные результаты.
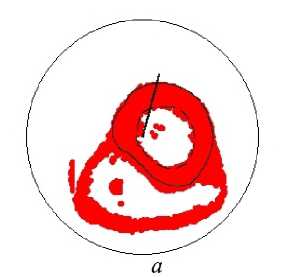
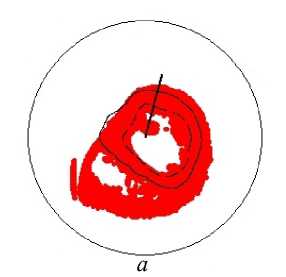
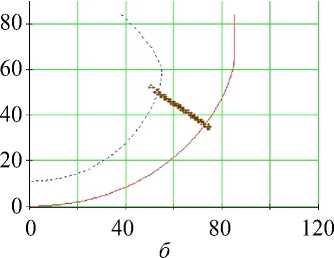
В верхней и средней части левого желудочка (см., например, рис. 13 и 14, а ) мы видим, что вертикальная ось проходит явно не через центр горизонтальных сечений левого желудочка, а находится ближе к межжелудочковой перегородке. Этот выбор положения оси левого желудочка связан с тем, что данная ось должна проходить через область верхушки левого желудочка, а проекция верхушки на плоскость его базы расположена не в центре базы. Если сместить ось в центр базы, то верхушка сердца будет расположена далеко от оси в одном из меридиональных сечений и мы не сможем приблизить форму стенок левого желудочка с помощью данной модели.
–30
–60
–90
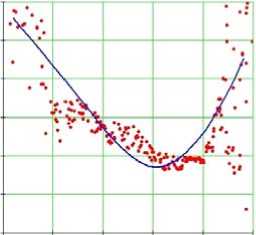
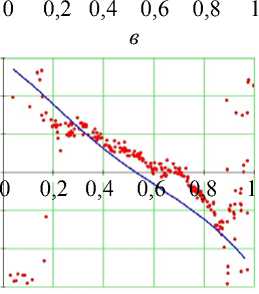
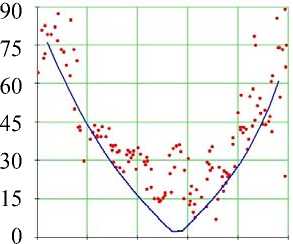
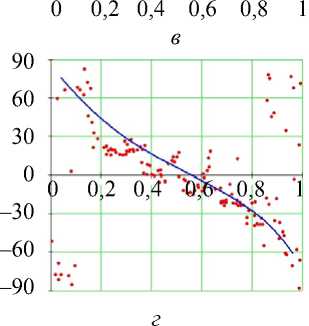
Рис. 14. Углы наклона волокон в модели и по данным эксперимента. Свободная стенка левого желудочка, средняя область (ψ = 35°), человек.
Обозначения как на рис. 7
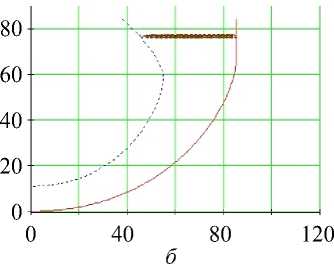
Рис. 13. Углы наклона волокон в модели и по данным эксперимента. Свободная стенка левого желудочка, область основания (ψ = 5°), человек.
Обозначения как на рис. 7
Проследим теперь за углами наклона волокон в одном из меридианов свободной стенки левого желудочка.
0 0,2 0,4 0,6 0,8 1
г
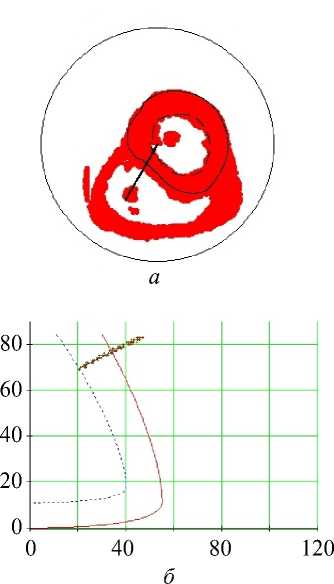
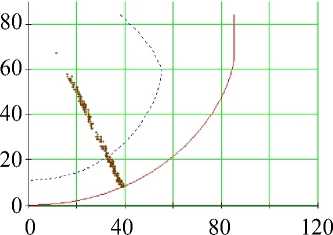
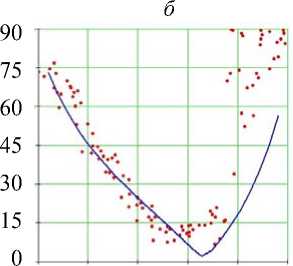
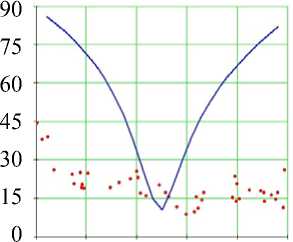
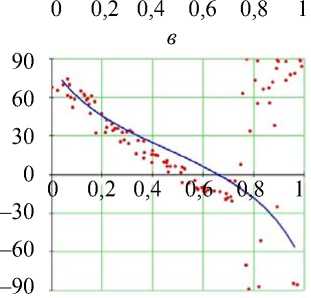
Рис. 15. Углы наклона волокон в модели и по данным эксперимента. Свободная стенка левого желудочка, область верхушки (ψ = 65°), человек. Обозначения как на рис. 7. Горизонтальное сечение ( а ) не приводится
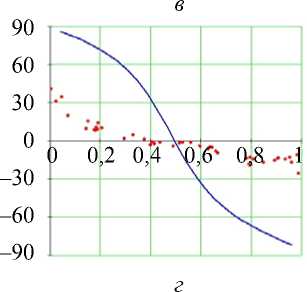
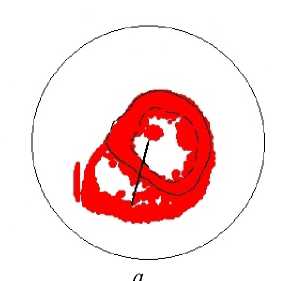
Рис. 16. Углы наклона волокон
в модели и по данным эксперимента. Межжелудочковая перегородка, область основания (ψ = 5°), человек.
Обозначения как на рис. 7
–30
–60
–90
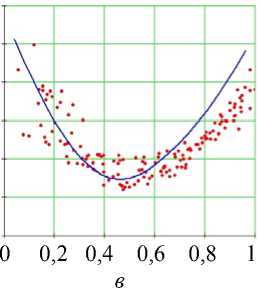
г
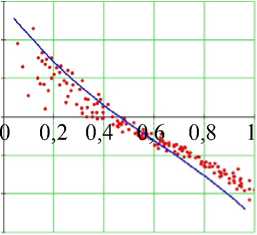
Рис. 17. Углы наклона волокон в модели и по данным эксперимента. Межжелудочковая перегородка, средняя область (ψ = 25°), человек.
Обозначения как на рис. 7
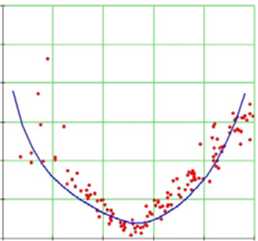
0 0,2 0,4 0,6 0,8 1
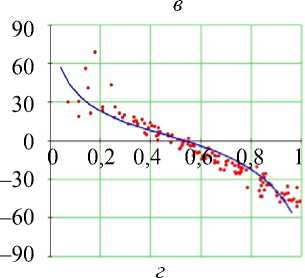
Рис. 18. Углы наклона волокон в модели и по данным эксперимента. Межжелудочковая перегородка, область верхушки (ψ = 45°), человек.
Обозначения как на рис. 7
В верхней части желудочка (см. рис. 13) угол истинного наклона волокон α (рис. 13, в ) в модели довольно точно повторяет данные томографии. Он убывает от 90° на эндокарде до примерно 25° в середине толщи стенки, а затем возрастает, достигая 70° на эпикарде. Винтовой угол (см. рис. 13, г ) в модели тоже довольно близок к данным эксперимента.
Средняя по высоте часть свободной стенки желудочка (см. рис. 14) демонстрирует нам существенно больший разброс значений обоих углов, но при этом их поведение в целом то же, что и в зоне основания, и оно вновь хорошо качественно и количественно воспроизводится моделью.
Об углах в нижней части свободной стенки левого желудочка (см. рис. 15) можно сказать практически то же самое. Заметим только, что в субэпикардиальной части стенки угол α возрастает значительно резче обычного, а угол α 1 не убывает, а возрастает, причем мы видим очень большой разброс значений этого угла.
Поведение обсуждаемых углов наклона волокон в верхней части межжелудочковой перегородки (см. рис. 16) в модели очень далеко от данных эксперимента.
В средней и нижней частях межжелудочковой перегородки (см. рис. 17 и 18) модель весьма точно воспроизводит углы наклона волокон.
Также в нашей модели, как и в модели [27], имитируется характерное взаиморасположение волокон в толще стенки желудочка, рассматриваемое в радиальном направлении ([27, рис. 14]). Это расположение Стритер ([31, рис. 42, с ]) назвал «японским веером».
Таким образом, предлагаемая в этой работе модель в основном адекватно воспроизводит направление волокон миокарда в левом желудочке.
Обсуждение
Этот раздел посвящен ограничениям построенной модели, способам ее верификации, ее возможному применению и дальнейшему развитию.
Ограничения
Наша модель адекватно воспроизводит углы наклона волокон в верхней и средней зонах свободной стенки левого желудочка, в средней и нижней области межжелудочковой перегородки сердца человека (в этих областях углы воспроизведены немного хуже в случае сердца собаки). Тем не менее согласие данных в области верхушки свободной стенки лишь качественное, а в верхней части межжелудочковой перегородки сердца человека модель дает результаты, которые полностью расходятся с данными эксперимента.
Неточное воспроизведение направлений волокон в зоне верхушки левого желудочка может быть объяснено с позиций ленточной концепции Торрента-Гуаспа. Согласно его теории (см., например, [20, 34]), миокард левого и правого желудочков образован из одной длинной целостной свернутой мышечной ленты, причем на левый желудочек и межжелудочковую перегородку в сумме приходится примерно три четверти длины ленты, а на правый желудочек – около одной четверти (так называемый правый сегмент, right segment). Особенно важно то, что верхняя часть (около двух третей) свободной стенки левого желудочка образована из одной области ленты (левого сегмента, left segment), а нижняя (приблизительно одна треть) – из другой области (нисходящего сегмента, descendent segment), не смежной с первой. Наша модель лучше повторяет свертку левого сегмента (наружная верхняя часть свободной стенки левого желудочка) и хуже – нисходящего и восходящего сегментов: в нисходящем сегменте хорошо воспроизведён ход волокон его области, близкой к левому сегменту (внутренняя верхняя часть свободной стенки левого желудочка), его нижней средней области (внутренняя нижняя часть свободной стенки левого желудочка и перегородки) и верхней области, близкой к восходящему сегменту (средняя между субэпи- и субэндокардом часть свободной стенки левого желудочка). В восходящем сегменте не воспроизводят данные томографии человека две небольшие области: одна примыкает к аорте, другая – к верхушке сердца. Остальные области восходящего сегмента соответствуют наружной части свободной стенки левого желудочка и перегородки, в них ход волокон воспроизведен хорошо.
Экспериментальные методы, которые можно использовать для верификации модели
В настоящее время существует несколько экспериментальных методов измерения направления волокон в сердце. Один из них – метод диффузионнотензорной магнитно-резонансной томографии, когда исследователь находит матрицу диффузии молекул воды в сердце. Главные направления диффузии определяются по структуре ткани [14, 15, 21, 39], и собственный вектор матрицы, соответствующий ее наибольшему собственному значению, дает нам направление волокна. Пространственное разрешение диффузионно-тензорной магнитно-резонансной томографии достигает 200 мкм [10]. Другой современный метод – это микроскопическая компьютерная томография, имеющая разрешение по пространству до 36–70 мкм [4]. Оба эти метода предоставляют данные высокого качества, которые можно использовать в компьютерных моделях.
Прямое измерение анизотропии также может быть проведено с помощью скрупулезного гистологического исследования направления волокон в пространстве [23, 31]. При этом проводят серию параллельных срезов сердца. На каждом срезе измеряют угол наклона волокна, что дает полную картину поля направлений волокон во всем сердце. Недавно Smaill с соавторами разработали метод комбинированной последовательной микроскопии высокого разрешения [36]. В этом методе после фиксации сердца проводится серия срезов, из которых получают последовательные изображения высокого разрешения. Затем, после обработки данных на компьютере, формируется целостная пространственная модель сердца.
В статье [18] волокна миокарда сердца плода человека были исследованы при помощи количественной микроскопии в поляризованном свете. Сердца были помещены в прозрачную смолу, полимеризованы и затем рассечены. После этого были измерены углы возвышения и азимута с помощью поляризованного света (подробнее см. [18]).
Сравнение с другими моделями
Экспериментальные данные об ориентации волокон могут быть использованы при конструировании вычислительных анатомических моделей:
-
– как дискретный набор данных в конечно-элементных моделях [13, 40, 41];
-
– для верификации моделей, основанных на правилах [5, 7, 16, 29].
Один из последних методов, основанных на правилах, – это алгоритм Лапласа– Дирихле [5], который получает на вход зашумленное поле ориентации волокон из диффузионно-тензорной магнитно-резонансной томографии и возвращает, во-первых, трансмуральные и апико-базальные направления для всего миокарда и, во-вторых, непрерывное и гладкое поле направлений волокон. Другой подход был использован Пескиным (Peskin), который получил поле направлений волокон исходя из принципа механического равновесия [25]. Чедвик (Chadwick) создал анатомическую модель, базируясь на принципах механической активности сердца: он рассмотрел цилиндрический левый желудочек и задал винтовой угол линейно зависящим от положения точки в стенке левого желудочка [9]. Беяр с соавторами (Beyar, Sideman) придал левому желудочку форму сфероида и также использовал линейную зависимость винтового угла от расстояния между точкой в стенке желудочка и эндокардом [6]. Интересный пример теоретического подхода принадлежит Bovendeerd с соавторами [8]. Они в 1992 г. сконструировали модель эллипсоидального левого желудочка, усложнили закон изменения винтового угла до кусочно-квадратичного и вычислили ориентацию волокон с помощью распределения винтового угла, которое было найдено при применении принципа механической адаптации, предложенного Артсом с соавторами (Arts et al.) в 1982 г. [3].
В данной работе мы представили модель архитектоники левого желудочка, основанную на правилах и включающую форму желудочка и ход волокон в его стенке. Полученный формализм существенно связан с идеей вложенных спиральных поверхностей Петтигрю [26], ленточной концепцией архитектоники желудочков сердца, разработанной Торрентом-Гуаспом [33], и анатомическими наблюдениями, представленными Стритером в его ставшей классической работе [31]. В рамках нашего подхода анизотропия сердца была получена на основе некоторых общих принципов. В нашей модели левый желудочек рассматривается как набор спиральных поверхностей, вложенных одна в другую. Каждая спиральная поверхность определена аналитически и является образом полукруга при некотором отображении. Первый шаг этой трансформации – отображение полукруга в прямоугольник в специальных координатах. На втором шаге мы определяем преобразование, переводящее специальные координаты в цилиндрические. Это преобразование непосредственно связано с формой эпикарда и эндокарда, полученной из данных, например, диффузионно-тензорной магнитно-резонансной томографии. В итоге мы получаем спиральные поверхности, заполненные кривыми (мышечными волокнами), являющимися образами хорд исходного полукруга, параллельных его диаметру (см. рис. 2).
Наша модель не единственная модель миокарда, основанная на идее заворачивания поверхностей. Синха с соавторами ( Sinha et al. ) в статье [30] предложили модель одного слоя миокарда, имеющего форму прямоугольника и обернутого вокруг (усеченного) конуса. Они использовали эту очень простую модель для изучения исчезновения самоподдерживающихся волн, вращающихся вокруг препятствий в случаях изотропии и анизотропии, но без связи с реальной картиной расположения волокон в желудочках сердца.
Для верификации нашей модели мы используем экспериментальные данные диффузионно-тензорной магнитно-резонансной томографии сердца собаки и человека в норме. В частности, модель адекватно воспроизводит как петлеобразную форму волокон, так и особенное трехмерное взаиморасположение волокон в стенке левого желудочка, которое Стритер сравнивал с японским веером.
Это достаточно точное воспроизведение моделью экспериментальных фактов позволяет нам рассмотреть модель как важный аргумент в пользу ленточной концепции архитектоники желудочков сердца, восходящей к Торренту-Гуаспу, так как модель, созданная на базе этой теории, выдает адекватное поле направлений волокон как следствие теоретических постулатов.
Сравним также нашу модель с другой моделью, основанной на правилах, в которой ориентация волокон устанавливается локально, а именно с моделью Bayer с соавторами, уже упомянутой выше в этом разделе [5]. Для сравнения можно использовать ориентацию волокон в различных частях левого желудочка. Модель Bayer строится по данным диффузионно-тензорной магнитно-резонансной томографии об анизотропии двух желудочков сердца собаки. Средняя невязка направлений волокон по данным модели и эксперимента составила 23°, т.е. мы не наблюдаем полного количественного воспроизведения моделью реальных экспериментальных данных, хотя имеется приемлемое соответствие. В частности, модель Bayer качественно повторяет анизотропию волокон в базальной зоне межжелудочковой перегородки лучше, нежели наша модель ([5, рис. 3]). В то же время наша модель лучше воспроизводит экспериментальные данные в средней по высоте зоне левого желудочка: мы получили характерный s-образный график угла α1 в трансмуральном направлении (рис. 8, г). В модели Bayer эта зависимость линейна по определению. Более того, если мы построим модель по формулам (1), (2) из обсуждемой статьи [5], то все графики угла α1, представленные на рис. 7–12, г, обнаружат независимость этого угла от широты и долготы нормали к эпикарду, вдоль которой вычисляется угол. Bayer с соавторами считают, что их модель легко может быть доработана с тем, чтобы учесть нелинейность угла α1. Но кроме этого необходимо еще сделать анизотропию широтно и долготно зависимой, что является непростой задачей. Наша же модель демонстрирует такую зависимость (рис. 7–12), что соответствует состоянию вещей в реальных сердцах, особенно в средней зоне левого желудочка.
Еще одно упрощающее предположение модели Bayer касается трансмурального вращения направлений волокон, которое Стритер назвал «японским веером» ([31, рис. 42, с ]). В этой модели вращение волокон определено лишь в одной плоскости, т.е. вокруг только одной оси, установленной трасмурально. Эта плоскость касается поверхности d = const, где d – это переменная, определенная в цитируемой работе Bayer [5] и описывающая положение точки в толще стенки; например, d = 0 на эндокарде и d = 1 на эпикарде. Более того, если оценить результаты, полученные в модели Bayer , по углу α 3 , определенному Стритером [31] и отражающему трансмуральное поведение ориентации волокон, этот угол будет постоянным и равным нулю, что является существенным упрощением. Эта особенность не позволяет отобразить положение волокон в трансмуральном направлении в толще стенки желудочка.
В нашей же модели, напротив, эта трехмерная структура принята во внимание и волокна на спиральной поверхности идут от субэпикарда до субэндокарда.
Итак, мы приходим к выводу, что обе эти модели имеют сильные и слабые стороны, а для преодоления указанных недостатков было бы полезно дальнейшее совершенствование обеих моделей.
Дальнейшее развитие и использование модели
Представленное здесь аналитическое описание геометрии сердца может быть использовано при построении новых численных методов для изучения электрофизиологической и механической активности левого желудочка. Поскольку наша модель представляет собой аналитически заданное отображение прямоугольного параллелепипеда в пространстве (γ, ψ, φ) в криволинейный левый желудочек, можно построить численную схему в прямоугольной области в координатах (γ, ψ, φ) (где граничные условия записываются наиболее просто) и учесть анизотропию явными аналитическими формулами. Данная модель также может быть использована для генерации различных анизотропных свойств сердца и изменения формы левого желудочка (путем изменения параметров модели) и изучения их влияния на электрическую и механическую функции сердца.
Заключение
Мы построили аналитическое описание анатомии левого желудочка сердца на базе ленточной концепции Торрента-Гуаспа и идеи спиральных поверхностей Петтигрю. Наша модель может быть использована как для верификации ленточной гипотезы, так и для проведения различных численных экспериментов при изучении влияния анизотропии на проведение возбуждения в сердце и при моделировании механической функции сердца. Модель продемонстрировала хорошее качественное и – в ряде областей стенки левого желудочка – количественное согласие поля направлений волокон с данными эксперимента.
Благодарности
Автор выражает благодарность своим научным руководителям и коллегам: из Института математики и механики УрО РАН – В.И. Бердышеву и Ю.Н. Субботину, из Института иммунологии и физиологии УрО РАН – Л.Б. Кацнельсону, В.С. Мархасину и О.Э. Соловьёвой и из Гентского университета (Бельгия) – А.В. Панфилову – за плодотворное участие в обсуждении изложенной модели.
Работа поддержана проектом 12-М-14-2009 Президиума УрО РАН, грантом 01SF1511 Гентского университета, Бельгия, Молодежным научным проектом Института математики и механики УрО РАН, Российским фондом фундаментальных исследований (проект 13-01-96048) и правительством Свердловской области.
Приложение.
Вычисление направления волокна в точке
Рассмотрим точку с цилиндрическими координатами (ρ, φ, z ). Для нахождения направления волокна в этой точке нужно:
sin (nY) / / / , / Й п z x =---V"( У Vmax - cos ф-(ру+рф Vim ax ))-cos Ф'Рф ' “ ' cos (П п —2^ x 2
sin (n Y ) / f . • / . f Й • п z
У = ' I x V max + sin Ф- ( РУ+РФ Ti m ax ) ) - sin Ф’Р ф ~ ' cos (n Y
Список литературы Неосесимметричная математическая модель анатомии левого желудочка сердца
- Правдин С.Ф., Бердышев В.И., Кацнельсон Л.Б., Соловьёва О.Э., Мархасин В.С. Статическая математическая модель архитектоники левого желудочка сердца человека//Современные проблемы математики: тез. докл. 42-й Всерос. молодежной шк.-конф., 30 января -6 февраля 2011. -Екатеринбург, 2011. -С. 311-314.
- Правдин С.Ф. Неосесимметричная модель формы и архитектоники левого желудочка сердца//Современные проблемы математики: тез. докл. Междунар. (44-й Всерос.) молодежной шк.-конф., января -2 февраля 2013. -Екатеринбург, 2013. -С. 131-134.
- Arts T., Veenstra P.C., Reneman R.S. Epicardial deformation and left ventricular wall mechanics during ejection in the dog//American Journal of Physiology. Heart and Circulatory Physiology. -1982. -Vol. 243, No. 12. -P. H379-H390.
- Aslanidi O.V., Nikolaidou T., Zhao Jichao, Smaill B.H., Gilbert S.H., Holden A.V., Lowe T., Withers P.J., Stephenson R.S., Jarvis J.C., Hancox J.C., Boyett M.R., Zhang H. Application of micro-computed tomography with iodine staining to cardiac imaging, segmentation, and computational model development//IEEE Transactions on Medical Imaging. -2013. -Vol. 32, No. 1. -P. 8-17.
- Bayer J.D., Blake R.C., Plank G., Trayanova N.A. A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models//Ann. Biomed. Eng. -2012. -Vol. 40, No. 10. -P. 2243-2254.
- Beyar R., Sideman S. A computer study of the left ventricular performance based on fiber structure, sarcomere dynamics, and transmural electrical propagation velocity//Circ. Res. -1984. -Vol. 55. -P. 358-375.
- Bishop M.J., Plank G., Burton R.A., Schneider J.E., Gavaghan D.J., Grau V., Kohl P. Development of an anatomically detailed MRI-derived rabbit ventricular model and assessment of its impact on simulations of electrophysiological function//Am. J. Physiol. Heart. Circ. Physiol. -2010. -Vol. 298, No. 2. -P. H699-H718.
- Bovendeerd P.H.M., Arts T., Huyghe J.M., van Campen D.H., Reneman R.S. Dependence of local left ventricular wall mechanics on myocardial fiber orientation: a model study//J. Biomechanics. -1992. -Vol. 25, No. 10. -P. 1129-1140.
- Chadwick R.S. Mechanics of the left ventricle//Biophysical Journal. -1982. -Vol. 39. -P. 279-288.
- Gilbert S.H., Sands G.B., LeGrice I.J., Smaill B.H., Bernus O., Trew M.L. A framework for myoarchitecture analysis of high resolution cardiac MRI and comparison with diffusion tensor MRI. Annual International Conference of the IEEE. Engineering in Medicine and Biology Society (EMBC). -2012. -P. 4063-4066.
- Grandi E., Pasqualini F.S., Bers D.M. A novel computational model of the human ventricular action potential and Ca transient//Journal of Molecular and Cellular Cardiology. Special Issue: Ion Channels. -2010. -Vol. 48, No. 1. -P. 112-121.
- Greenstein J.L., Winslow R.L. Integrative systems models of cardiac excitation-contraction coupling//Circ. Res. -2011. -Vol. 108. -P. 70-84.
- Gurev V., Lee T., Constantino J., Arevalo H., Trayanova N.A. Models of cardiac electromechanics based on individual hearts imaging data: Image-based electromechanical models of the heart//Biomech. Model. Mechanobiol. -2011. -Vol. 10, No. 3. -P. 295-306.
- Helm P., Beg M.F., Miller M.I., Winslow R.L. Measuring and mapping cardiac fiber and laminar architecture using diffusion tensor MR imaging//Ann. N. Y. Acad. Sci. -2005. -Vol. 1047. -P. 296-307.
- Helm P.A., Tseng H.J., Younes L., McVeigh E.R., Winslow R.L. Ex vivo 3D diffusion tensor imaging and quantification of cardiac laminar structure//Magnetic Resonance in Medicine. -2005. -Vol. 54. -P. 850-859.
- Hren R. A realistic model of the human ventricular myocardium: application to the study of ectopic activation: Ph.D. Thesis. -Halifax, Nova Scotia, Canada: Dalhousie University, 1996. -269 p.
- Hunter P.J., McCulloch A.D., ter Keurs H.E. Modelling the mechanical properties of cardiac muscle//Prog. Biophys. Mol. Biol. -1998. -Vol. 69. -P. 289-331.
- Jouk P.S., Usson Y., Michalowicz G., Grossi L. Three-dimensional cartography of the pattern of the myofibres in the second trimester fetal human heart//Anat. Embryol. (Berl). -2000. -Vol. 202, No. 2. -P. 103-118.
- Ter Keurs H.E., Shinozaki T., Zhang Y.M., Zhang M.L., Wakayama Y., Sugai Y., Kagaya Y., Miura M., Boyden P.A., Stuyvers B.D., Landesberg A. Sarcomere mechanics in uniform and non-uniform cardiac muscle: a link between pump function and arrhythmias//Prog. Biophys. Mol. Biol. -2008. -Vol. 97, No. 2-3. -P. 312-331.
- Kocica M.J., Corno A.F., Lackovic V., Kanjuh V.I. The helical ventricular myocardial band of Torrent-Guasp//Seminars in Thoracic and Cardiovascular Surgery: Pediatric Cardiac Surgery Annual. -2007. -Vol. 10, No. 1. -P. 52-60.
- Lunkenheimer P.P., Redmann K., Kling N., Jiang X., Rothaus K., Cryer C.W., Wübbeling F., Niederer P., Heitz P.U., Ho S.Y., Anderson R.H. Three-dimensional architecture of the left ventricular myocardium//The Anatomical Record Part A. -2006. -Vol. 288. -P. 565-578.
- Niederer S.A., Hunter P.J., Smith N.P. A quantitative analysis of cardiac myocyte relaxation: a simulation study//Biophys. J. -2006. -Vol. 90, No. 5. -P. 1697-1722.
- Nielsen P.M.F., LeGrice I.J., Smaill B.H., Hunter P.J. Mathematical model of the geometry and fibrous structure of the heart//Am. J. Physiol. -1991. -Vol. 260. -P. H1365-H1378.
- O’Hara T., Virag L., Varro A., Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: Model formulation and experimental validation//PLoS Comput. Biol. -2011. -Vol. 7, No. 5:e1002061.
- Peskin C.S. Fiber architecture of the left ventricular wall: An asymptotic analysis//Communications on Pure and Applied Mathematics. -1989. -Vol. 42, No. 1. -P. 79-113.
- Pettigrew J. On the arrangement of the muscular fibers of the ventricular portion of the heart of the mammal//Proc. Roy. Soc. -1860. -Vol. 10. -P. 433-440.
- Pravdin S.F., Berdyshev V.I., Panfilov A.V., Katsnelson L.B., Solovyova O., Markhasin V.S. Mathematical model of the anatomy and fibre orientation field of the left ventricle of the heart//Biomedical Engineering Online. -2013. -Vol. 54, No. 12. -21 p.
- Rice J.J., de Tombe P.P. Approaches to modeling crossbridges and calcium-dependent activation in cardiac muscle//Prog. Biophys. Mol. Biol. -2004. -Vol. 85, No. 2-3. -P. 179-195.
- Seemann G. Modeling of electrophysiology and tension development in the human heart: Ph.D. Thesis. -Karlsruhe: Universitat Karlsruhe, 2005. -234 p.
- Sinha S., Stein K.M., Christini D.J. Critical role of inhomogeneities in pacing termination of cardiac reentry//Chaos: An Interdisciplinary Journal of Nonlinear Science. -2002. -Vol. 12, No. 3. -P. 893-902.
- Streeter D.D.J.R. Gross morphology and fiber geometry of the heart//Handbook of Physiology. -Sec. 2, Vol. 1. -Bethesda, Maryland: Am. Physiol. Soc., 1979. -P. 61-112.
- Sulman T., Katsnelson L.B., Solovyova O., Markhasin V.S. Mathematical modeling of mechanically modulated rhythm disturbances in homogeneous and heterogeneous myocardium with attenuated activity of Na+ -K+ pump//Bull. Math. Biol. -2008. -Vol. 70, No. 3. -P. 910-949.
- Torrent-Guasp F. The Cardiac Muscle. -Madrid: Fundacion Juan March, 1973.
- Torrent-Guasp F., Kocica M.J., Corno A.F., Komeda M., Carreras-Costa F., Flotats A., Cosin-Aguillar J., Wen H. Towards new understanding of the heart structure and function//European Journal of Cardio-thoracic Surgery. -2005. -Vol. 27. -P. 191-201.
- Trayanova N.A., Constantino J., Gurev V. Electromechanical models of the ventricles//Am. J. Physiol. Heart Circ. Physiol. -2011. -Vol. 301. -P. H279-H286.
- Trew M.L., Caldwell B.J., Sands G.B., LeGrice I.J., Smaill B.H. Three-dimensional cardiac tissue image registration for analysis of in vivo electrical mapping//Ann. Biomed. Eng. -2011. -Vol. 39, No. 1. -P. 235-248.
- Ten Tusscher K.H., Panfilov A.V. Alternans and spiral breakup in a human ventricular tissue model//Am. J. Physiol. Heart Circ. Physiol. -2006. -Vol. 291. -P. H1088-H1100.
- Ten Tusscher K.H.W.J., Noble D., Noble P.J., Panfilov A.V. A model for human ventricular tissue//Am. J. Physiol. Heart Circ. Physiol. -2004. -Vol. 286. -P. H1573-H1589.
- Vadakkumpadan F., Arevalo H., Prassl A.J., Chen J., Kickinger F., Kohl P., Plank G., Trayanova N. Image-based models of cardiac structure in health and disease//Wiley Interdiscip. Rev. Syst. Biol. Med. -2010. -Vol. 2, No. 4. -P. 489-506.
- Vicky Y.W. Modelling In Vivo Cardiac Mechanics using MRI and FEM: Ph.D. Thesis. -Auckland: Bioengineering Institute, The University of Auckland, New Zealand, 2012.
- Zhang Y., Liang X., Ma J., Jing Y., Gonzales M.J., Villongco C., Krishnamurthy A., Frank L.R., Nigam V., Stark P., Narayan S.M., McCulloch A.D. An atlas-based geometry pipeline for cardiac Hermite model construction and diffusion tensor reorientation//Medical Image Analysis. -2012. -Vol. 16, No. 6. -P. 1130-1141.


