Непогружаемость m-мерных метрик вращения в виде геликоидальной поверхности в (m+1)-мерное евклидово пространство

Непогружаемость плоскости Лобаческого в Е3 доказана Д. Гильбертом [1], а погружаемость в Е” при и > 5 установлена в работах [2, 3]. Вопрос о погружении плоскости Лобачевского в Е4 (без дополнительных ограничений на вид погружения, кроме его регулярности) остается открытым. В работе [4] Э.Р. Розендорн доказал невозможность погружения плоскости Лобачевского в Е4 в виде геликоидальной поверхности. Невозможность погружения плоскости Лобачевского в Е4 исследовалась также в работах [5-8].

В работе [9] доказана теорема: если В_и (и) - неограниченная функция при - оо < w < +оо, то метрика ds² = ^w² + В² (и) ■ dv² не допускает изометрического погружения в Е" (и > 3) в виде геликоидальной поверхности.

Следуя Э.Р. Розендорну [4], назовем поверхность геликоидальной, если после приведения ее метрики к виду ds² = du² + 5²(w) ■ (<7wj + ... + du²) коэффициенты вторых квадратичных форм и коэффициенты кручения зависят только от координаты и_х . Примером может служить прямой геликоид в пространстве Е³.

В настоящей работе рассматривается вопрос о погружении в Em+1 «-мерных метрик вращения ds2 = du2 + B2(u)-(du2 +... + dul)                          (1)

в виде геликоидальной поверхности.

Теорема. Если В_и (и) - неограниченная функция при - оо <  и_х < +=о, то метрика ds² = du² + В²(и) • (du₂ +... + du² ) не допускает изометрического погружения в Е^т+| в виде геликоидальной поверхности.

Доказательство: Пусть F - «-мерная односвязная поверхность в Em+1 с внутренней метрикой неположительной кривизны. Будем считать, что на Ет введена единая система координат (к,, w2,...,wm), а поверхность F задана вектор-функцией г^их, и2,...,итУ Как обычно, or        д2г г, =---, г„ =------, i,j = 1, 2, ...,т. Зафиксируем вдоль F ортонормированный базис норди,      duft^

мали е¹. Коэффициенты первых основных форм находятся по формулам gy^r^, i,j = 1, 2, ...,т, т.е. g_H = 1, g_y = В²(и_х) при i = j и g_y = 0 при z ^ j, коэффициенты вторых квадратичных форм - по формулам Ь_у = r_ye\ i,j = 1, 2, ...,т.

Уравнения Гаусса, Петерсона-Кодацци, Риччи имеют вид:

к=\ где i,j,k = 1, 2, ...,т.

Ершова А.В.

Непогружаемость т-мерных метрик вращения в виде геликоидальной поверхности в (т*1)-мерное евклидово пространство

Для метрики (1) коэффициенты Кристоффеля Г_х

^1)

#0,)

, Г^, =-В(их) • B„4ux),

t = 2, ...,т , а остальные равны нулю.

„            Эд

Используя равенства частных производных---г. =--- г_1ки ди_к ди.

ди,

5 ,

=---е„ , получаем систе- ди, '

му уравнений:

ди, ди,

^Гк)-^Гк) = ^^^-ь^, уди, ди, ^                  ькк

где i, j,l = 1,2, ...,т . Сделаем замену:

by, если i = 7=1, by -В1их\ если /* j,

Ь\ • В² (и, ), если / = у * 1.

1 »

Тогда

дих

ecmi = j = l, дих

(b\ yBlu^A-bV- В 1их), если i * j, дих                         1

(6‘) • В² (и,) + 2Ьу ■ В(и_х) • В (и_х ), если i = j * 1, ди_х                                     ¹

где i,j = 1, 2, ...,т .

Будем считать, что коэффициенты вторых квадратичных форм и коэффициенты кручения зависят только от координаты и_х . Умножим первое уравнение системы (2) на by и сложим полученные уравнения. Из второго уравнения системы (2) несложно получить равенства, которые будем использовать в дальнейшем:

bn-b.t-M =--, t = 2,...,m.                     (3)

В(их)

Тогда справедливо равенство:

®«A^U^ , z.i 1.1 b^OV)

—! + Ьхх  ! В(их)           В(их)

Можно заметить, что:

т

Положим

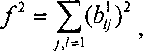
и воспользуемся равенствами (3), тогда

0,5- —(/²) = -^^-(/²)-(^-1)- ди_х           В1и_х)

ВЧ^

0,5~(/²) + ^2-(/²) = -(z»-1)- ди_х         В(и_х)

Я2(М])

Серия «Математика, физика, химия», выпуск 8

Математика

Умножим правую и левую часть уравнения на 2В¹ (и^. Тогда

В2^У         2ВМ-В., М (JI') = "Цт -1)' Вн (и,) ■ В («,), оих         1             111

т.е.

^-(В¹ (и,). f ) = -2(™ -1). В„(и.) • В („,).

OU_X             111

В итоге получаем равенство: f²B² (ц) = -(т -1) ■ В²^(и^+С. Если функция В_и^ (и_х ) не ограничена, то это равенство выполняется не для всех значений и_х.

Теорема доказана.