Непогружаемость метрик вращения в виде геликоидальной поверхности в w-мерное евклидово пространство

Непогружаемость плоскости Лобаческого в Е3 доказана ДГильбертом [1], а погружаемость в Е” при и > 5 установлена в работах [2, 3]. Вопрос о погружении плоскости Лобачевского в Е4 (без дополнительных ограничений на вид погружения, кроме его регулярности) остается открытым. В работе [4] Э.Р. Розендорн доказал невозможность погружения плоскости Лобачевского в Е4 в виде геликоидальной поверхности. Невозможность погружения в Е4 исследовалась также в работах [5-10].

В настоящей работе рассматривается вопрос о погружении в Е” двумерных метрик вращения ds² = du² *B²(u)dv²                               (1)

в виде геликоидальной поверхности. Следуя Э.Р. Розендорну [4], назовем поверхность геликоидальной, если после приведения ее метрики к виду (1) коэффициенты вторых квадратичных форм и коэффициенты кручения не зависят от координаты v. Примером может служить прямой геликоид в пространстве Е3.

Теорема. Если В_и (м) - неограниченная функция при -оо < ы < +оо, то метрика ds² -du² + B²(u)dv² не допускает изометрического погружения в Е“ (п>3) в виде геликоидальной поверхности.

Доказательство: Пусть F - двумерная односвязная поверхность в Е” с внутренней метрикой неположительной кривизны. Будем считать для простоты, что на F введена единая система коор-5г Э2г динат (u,V), а поверхность F задана вектор-функцией r(«,v). Как обычно, г, = —г, г« = —:—г, ди1       du’duJ i,j = 1,2, где их=и, u2=v. Зафиксируем вдоль F ортонормированный базис нормалей eb...,e„_2. Хорошо известно, что коэффициенты первой и второй основных форм gy^ry,

/,У = 1,2, Ma =r12ea, La =rnea , Na -r22ea , a = 1, 2,..., и-2; и так называемые коэффициенты кручения Аарк = —^вр, к = 1,2, удовлетворяют нижеследующей системе уравнений (2)-(5). Эи

Уравнения погружения двумерной поверхности в Е” имеют вид (a = 1,2,..., п-2):

п-2

^LaNa-M2y^EG-F2y(2)

Й Й

—М, -^к-Г^-Г^ + Г^-Г^ + ЭД^-М^,(3)

'аЛ=+S(^-^1 -мрА^.< c/V        ОН

Уравнение погружения метрики вращения ds² = di? + В² (и) • dv² в Е^п: ds² = г²du² + 2r_ur_vdudv + r²dv²,

Гпазырина А.В.

Непогружаемость метрик вращения в виде геликоидальной поверхности в n-мерное евклидово пространство где г2 = Е = 1, 2rMrv = F = 0, г2 = G = В2 (и) и К = -5м. _ кривизна метрики, В

EG-F² = B², —Ь_а=—М_а=—А„_х=й и gⁿ=l, g²¹=-l—, ’ dv ^а dv “ dv ^ ^s ’ ^s B²^

коэффициенты Кристоффеля примут вид:

r1 —

1 н ~

0,5EuG-FFu+0,5EvF

EG-F2

= 0;

Г2 _0,5GuE-0,5EvF

1 12--

EG-F2

= Д,.

В ’

р2 _FuE-0,5EEv-0,5EUF 1 п -

Г¹ — ¹12 -

EG-F² 0,5E_vG-0,5G_uF

= 0;

. _FvG-0,5G„G-0,5GvF

1 22--

EG-F2

= -В„В;

EG-F2

= 0;

,₂ 0,5G_vE-F_vF + 0,5G„F

22 -

EG-F2

= 0,

тогда наша система примет вид: л-2

а=1

Ама=-Ь

Эи В

®ии ^2 .

В ’

л-2

(аД2~^Д^1)^

Р=^ ^м.^м^-х^у, с р=\

д .

д^ЛаР2

Сделаем замену: М_х = т_хВ(и);

л-2

⁼ X (^а/2^Д/1 ^{- А}аг\^АРг2 ) ⁺ ^„Lp - L_aMp ) +

NaMp-MaNp

В2

Nx=nxB2^-,

Lx=lx;

Аху\ - axyi;

•j-M, =1Г^тхВ^ + т_хВ (м); ди     ди

!-N_x = ^-n_xB²(u) + 2n_xB(u>B„^;

ди     9и

-^Aap2 = ^aap2B(u) + aap2Bu^; VIA        VW

Axy2=axy2B^’

где x,y = a,p.

и первое, и третье уравнение разделим на В² (и^-) , а второе и четвертое - на В(и). Система уравнений примет вид:

Л-2 ,, D а=1

д _BU\

^та= -2та-^ + Х\1Раар2 "тра«р\);

д         Ви , Ви ti,'

Т-»а                   \^тр^аар2-^пр^аар\)’

014           -D 15 р_^

9    _

^2— Мг

V + Е ^«Г^РП " ^а«г\^аРг2 ) ^{+ т}а¹Р "¹а^тр* ^па^тР "^р-

С /=1

Умножим уравнения (2), (3) и (4) соответственно на т_а, п_а, а_ар₂ и сложим полученные уравнения:

ПД( д

> т„ —т„ + п„ —п„ + а„_Д9 —а~_Я7 ^\\ ди ^а “ди “ ^аР²ди “^р2

Р*а

- ^а в П“ В *П“1“ В а“^2 В +   ’

Серия «Математика, физика, химия», выпуск 7

Математика л-2   л-2                     л-2   л-2                      л-2     л-2

где £ = ^ т_а ^ QpU_ap₂ - тп_ра_ар_Х) +^ п_а ^Г(тра_ар₂ - Пра_ар_Х) + £ а_ар₂ ^ (^г^Ду! ~ ^аау1°Д/2 ) + а=1    /7=1                         а=1   /7=1                          а=1       /=1

Р*а п-1

+ Е ^a»pi (^та¹р "^р* »а^тр -т_аПр^ = О.

а=1

Р*а

Можно заметить, что:

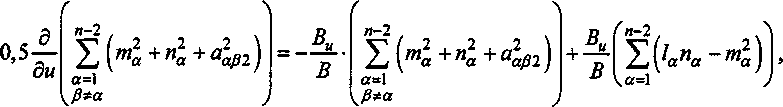
где Е Va^a ~та) = —и обозначим £ (w2 + л2 + а^ \ = f2, тогда а=1                 "                а=1

Р*а

0,5—/2 = -^-/2-^^-;         0,5—/2+^./2=-^-^ (умножим на 2S2);

duJ В J В2                  ди В J В2

ои                                     оих '

В итоге мы получим: f²B² (м) = -В² (и) + С. Равенство не выполняется для всех значений и, если функция В_и(«) не ограничена. Теорема доказана.

Следствие. Плоскость Лобачевского Z² (-1) не допускает изометрического погружения в Е^п (л > 3) в виде геликоидальной поверхности.

Замечание. Если Л„(м) ограничена, то метрика (1) допускает погружение в виде геликои дальной поверхности в Е3 хх =^-S(«)cosCv, Х2 = -^B(u)sinCv, х3 = -^^С2-В2 du

, здесь х_х,

х₂, х₃ - декартовы прямоугольные координаты в Е³, |В„ | < С = const.