Несимметричная задача про счастливые билеты

DOI:

Классическая задача про счастливые билеты формулируется следующим образом. Есть пачка билетов, каждый из которых имеет номер, состоящий из 6 цифр. Первый билет имеет номер 000000, а последний 999999. Билет считается счастливым, если сумма первых трех цифр его номера равна сумме трех последних цифр номера. Так, например, счастливым считается билет с номером 331520. Нужно определить количество счастливых билетов в пачке. Задача сводится к определению количества решений диофантового уравнения г + j + к = I + т + q, где каждая из переменных есть цифра. Решение этой задачи приведено, в частности, в книге [1], где формула

S =

1 Г 2 sin ⁶ 101 ^ -_ z sin ⁶ 1

dt

получена с применением техники комплексного анализа. Эта формула легко обобщается на случай, когда номер билета состоит из 2п цифр М -ричной системы.

1.    Постановка задачи

Рассмотрим обобщенную задачу, когда номер билета состоит из 2п + к элементов, каждый из которых пробегает множество значений из множества М = { 0,1, 2,..., М — 1 } . Билет считается счастливым, если сумма первых п элементов равна сумме последних п + к элементов. Задача сводится к подсчету числа N(п,М,к) — количества решений уравнения п         п        к

52 ж = Т.Уз + 52 z , г=1       j=1      j=1

где ж _г Е ММ, у , Е М, Z j Е М.

2.    Вспомогательные тригонометрические тождества

Предварительно докажем несколько лемм.

Лемма 1. Имеет место тождество м-1

52 cos (гж+ у) = г =0

sin М sin 2

, М — cos( 2

- ж + у).

Доказательство. Воспользуемся известными соотношениями [3]

м

52 cos Зж = j=0

cos

Мж sin ^м + ¹ ж

"2 sin 2

м

52 sin Зж = sin j=0

Мж sin ^М +1 ж

"2 sin ²

Получим:

м - 1	м - 1	м - 1
52 cos (гж + y)	= cos y 52 cos гж —	sin у 52 sin гж
г =0	г =0	г =0

М — 1 sin М^          М — 1 sin М^ sin М^ М — 1 _х

= cosy cos ж---- 2 --siny sin ж----2- =---- 2- cos ( ж + у).

2 sin 2                  2 sin 2 sin 2 x 2'

Лемма 2. Имеет место тождество:

^м -¹                      _sin 2 М2

52 cos(ж(г — j)+ P) = ■ 2 2 cosp.

sin ² 2

»,j=0

Доказательство. Обозначим р — j х = ш, — р — М ^-1 = ш и применим два раза лемму 1.

М - 1                     М - 1 М - 1

У cos ((г — j)х + р) =ЕЕcos (гх + ш) = i,3=0                           3=0 i=0

М ^-1 sln М ^х М

=       2- cos( —

^ sin х 3 =0       ²

-

Л                  • Мх М - 1

1               Sln 2  \^

• -х + р — гх) =---- 2— / cos (гх + ш) =

sln х

sin

2 Мх

sin ² х

, М —

cos<—

1       .

• - х + ш)

3.    Обобщение формулы для числа счастливых билетов

sin ² М sin ² х

cos р.

Далее воспользуемся методом тригонометрических сумм [2]. Для этого введем в рассмотрение дискретную дельта-функцию 5 : Z ^ { 0,1 } , определенную следующим образом:

( 1,х = 0,

[0,х G Z/ { 0 } .

Тогда искомое число можно записать в виде п        пп

N (п,м,к) = У ••• У 5(Ух« — У Уз — У г,).

х1       zk i=1       3=1

Здесь и далее в суммах, в которых не указаны границы суммирования, подразумевается суммирование от 0 до М — 1. Функцию 5(х) можно задать аналитически выражением, например, следующим образом:

5(х) = — [ cos (tx)dt.(5)

^ Jo

Подставим равенство (5) в выражение (4). В результате получим

1                      Р'Л"            п

N(п,М, к) = - ∑︁ _··· ∑︁ ₀ cos ^{^ (} У ^{( x} i ^— y i ) ^— У ^г з ^{) dt}.

Поменяв местами суммирование и интегрирование, получим выражение

N(М, п,к) = —у N(п, М, k,t)dt,(6)

где пк

• NJ(n,M,k,t)= У ... У У ... У cos(t У(Xi — yi) — t Угз).(7)

Ж1,У1 х„<у„ zi        zk          i=1

Упростим формулу (7). Для этого поменяем местами порядок суммирования:

пк

Е ••• ЕЕ ••• Е ^ Е (х - у . ) - « Е « )

2k       21 жп,уп     м,У1         i=1

и выполним внутреннее суммирование, использовав лемму 2:

пк

52 cos (t(x i - y i ) + t ^( X i - у . ) - t^ ^ j ) =

Ж1,У1                          i=2

sin

2 Mt

sin

2 t

п                 к cos (t ^(Xi - yi) - tJ2 4).

i =2                 j =1

С учетом этого будем иметь sin

N (n,M,k,t) =-- sin

: Mt                                     пк

24- Е- ЕЕ ••• Е cos(t Е (x i - y . ) - 1 Е =л

• 2    2k       21 ж„,у„     Ж2,У2         i=2

Последовательно выполнив в последнем равенстве суммирование по парам индексов

Х2,У2, X3,У3, ..., xn,yn, получим выражение i 2n Mtк

N(n,M,k,t)Msn2n5b E-E cos(tE-j).(8)

sin    Г).

2 2k       Z1

Мы учли, что cos x есть четная функция. Внутреннее суммирование в формуле (8) произведем, использовав лемму 1.

кк

«os ^(t 52 ^z j ) = 52^{cos (t} ^ i ⁺ 52 ^z j ) =

Z1         j=1         Z1

sin M sin 2

cos (

M - 1

к t + е j,).

j =2

Выполним суммирование по индексу

^:

к

ЕЕ cos(t Е j ) ) =

2 2     2 1

j =i

sin Mt

2- > cos( sin t           v

2    2 2

M - 1

^{1 +}

к

Е j-) = j=2

sin M

sin 2

52 cos (j 2 t +

M - 1

к

+Е jj) = j=3

sin

2 Mt

sin

2 t

cos (2

M -

~ t +

к

Е j j ).

j =3

После выполнения суммирования по всем оставшимся индексам z ₃ ,..., z ^ получим вы-

ражение

~                 sin2”+fc Mt

^N(n,M^,k,t) =   . _к 2 ^cos(-^{( M} — l)t).

sin 1  2

Подставим выражение (9) в равенство (6) и сделаем замену t = 2х. Искомое выражение для числа решений имеет вид:

N (п, M,B = - Л 41 Мх cos (к(М — 1)x)dx.(10)

7Г JoSin

Формула (1) есть частный случай формулы (10) при к = 0,п = 3, М =10.

4. Асимптотика

Получим оценку величины N(п,М, к), используя метод стационарной фазы [4]. Искомый интеграл (10) можно представить в виде двух слагаемых, первое из которых есть интеграл от той же функции на интервале (0, ^ ), а второе — на интервале ( ^ , ^ ). На рисунке для примера изображен график функции д(х) = ⁸^°^х .

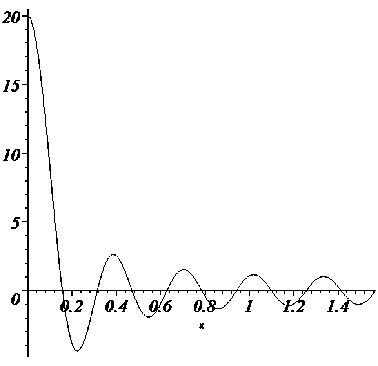
График функции д(х) = sisnn²^

Поскольку подынтегральная функция имеет вид д^{2тг + к} (х) cos ^х, то можно сделать вывод, что при больших значениях 2п + к основной вклад в интеграл (10) дает первое слагаемое. Функцию /(х) = sin^ разложим в ряд Маклорена:

/ (х) = М — -М (М ² — 1)х ² + о(х ³ ).

Тогда при малых х имеем приближенное равенство ln/(х) « ln (М(1 — —---—х2)) =

= 1пМ + ln (1 — ^М 2 - ¹ х ² ) « 1пМ — ^М 2 - ¹ х ² .

Использовав формулу / 0 ^ю е ^b 2 ^x cos'Xxdx = 2 | Ь | е 4ь ² из публикации [3], получим искомую оценку, обозначив 2п + к = t, k(M — 1) = д, ^м 6-¹ = b ² , b > 0:

N (п, M, k) = — [ / * (x)cos^xdx ^ Jo

2 Г^              ,

— J / * (x) cos ^xdx =

2 Г ^

^ Jo

e^b ln ' ^{( x )} cos^xdx = — /  e * ln ^{м tb} 2 ^x 2 cos^xdx

^ Jo

—M * / e ^tb 2 ^x 2 cos^xdx ^     Jo

² M * ^e-^. ^    2bVt

Возвращаясь к исходным величинам, получим асимптотику

„         M * I 6             з/= ² (м+i)                          _z _

^N ^^М’^к) “v M 2 —г V?(5^+k ^{eW -1}” - ⁺⁴ .           <^{n )}

Учитывая, что VM ² — 1 ^ M , получим более простую формулу

N (n,M,k)

_           6         -   3fe ² (M+1)

^M \] ^(2n + k) ^{e 2(M -1 )(2} "^+k) .

При к = 0 получим асимптотику для классической симметричной задачи:

N^zM^, 0)

M ^{t -}\ . ^п

Приведем примеры вычислений по формуле (11). Рассматриваем случай билетов, номера которых состоят из 6 цифр. Билет считается счастливым, если сумма двух первых цифр равна сумме последних четырех цифр.

В принятых в статье обозначениях нужно определить N (2, M, 2). Ниже в таблице приведены оценки значений этой функции, вычисленные по формуле (12), точные значения и относительная погрешность 5 (в процентах):

M	10	11	13	20
асимптотика	25019,33	39653,22	89161,66	731451,42
точное значение	25927	41118	92547	760704
5	3,5	3,56	3,66	3,84

Как видим, во всех рассмотренных случаях формула (11) дает достаточно точные оценки, и погрешность не превышает 4 %.

Заключение

В статье рассматривается обобщение задачи о счастливых билетах, когда подсчитываются суммы первых п цифр и последних п + к цифр в системе счисления по основанию M . Получено интегральное представление (10) для количества таких билетов. Методом стационарной фазы получена оценка искомой величины.