Нестационарное температурное поле в параллелепипеде в режиме теплопроводности при граничных условиях первого рода

При анализе кондуктивно-ламинарной свободной конвекции в замкнутых объёмах уравнения Обербека-Буссинеска могут быть представлены в несопряжённом виде [1]. Для плоских и осесимметричных геометрий в [2, 3] имеется множество решённых задач теплопроводности, но следует отметить, что анализ пространственных постановок представлен недостаточно. В [4] приведены методы получения аналитических решений, однако метод конечных интегральных синус-преобразований является наиболее эффективным [5].

В связи с этим, на примере области в форме параллелепипеда при граничных условиях первого рода демонстрируется алгоритм получения аналитического решения с помощью преобразования Лапласа по временной переменной и конечного интегрального синус-пре-образования по геометрическим координатам.

Рассматривается задача нестационарного распределения температуры по механизму теплопроводности в параллелепипеде при гранич-

Применение конечного интегрального синус-преобразования по безразмерной координате ¹ :

Fy [Tl (X, Y, Z)] = Fy (X, Z) = j T (X, Y, Z )sm(AY )dY, где jU - корни уравнения sin д = 0 ; с учётом

того, что

FY

d ² T_L dY²

F Y

ных условиях первого рода.

д t     — Г д ² t д ² t д ² t )

=+т+; дт   pcp (дx2   ду2   дz2 J t (0, у, z ,0 ) = t1; t (x, у, z ,0) = 0;

t ( h₁, у, z, 0 ) = t ( x ,0, z, 0 ) = t ( x, h ₂, z, 0 ) = = t ( x , у ,0, 0 ) = t ( x , у , h ₃, 0 ) = 0.

- В ² Ф Y ; F y

d ² T_L dZ^T

d ² T_L

dX1

d ² Ф _Y . dZ ^{2 ;}

d ² Ф _Y . dX ^{2 ;}

F y [ 1 ] = - —( cos В - 1 ) ; В

FY [s ' ] = —— (cos д — 1); Bs переводит исходную задачу в изображение: d ФУ      d ФУ (    2          л Z1

—2^ + ^{B 2}— 2^ ^-( A²д ² + ^s ) Ф Y = 0; ⁽¹⁰⁾

dX      dZ

Введём безразмерные координаты: x v z X

X = — ; Y = ^у- ; Z = —; a = ^—— ; h l       h 2        ^h 3       PC p

Ф Y ( 0, Z , s ) = —L ( cos д — 1 );    (11)

B s

Ф Y ( 1, Z , s ) = Ф Y ( X ,0, s ) = Ф Y ( X ,1, s ) = 0. (12)

Повторное применение синус-преобразо-вания по безразмерной координате Z преобразует систему (10)-(12) в систему обыкновенных дифференциальных уравнений следую-

щего вида:

A =

h L; B = B; » = a ^; T = L_ , h 2         ^h 3         ^h₁          t 1

dX- ^- ( ^{B 2} Y ² + A ² В ² + ^s ) ^Ф XY = 0;

Ф XY ( 0, s ) =

тогда система (1)-(3) примет следующий вид:

( cos д - 1 )( cos у - 1 ) BY s

д T   д² T   ,₂ д² T . д² T

--—---2—+ A --Т + B --Т ;

д 0  д X ²     д Y ²     д Z ²

T ( X , Y , Z ,0 ) = 1; T ( X , Y , Z ,0 ) = 0;

T ( 1, Y , Z , 0 ) = T ( X ,0, Z , 0 ) = T ( X ,1, Z , 0 ) = = T ( X , Y ,0, 0 ) = T ( X , Y ,1, 0 ) = 0.

Ф YZ ( 1, s ) = 0.

Решение (13)-(15) таково:

Ф YZ ( X , s ) = - ^{2 ( cos д - 1 )( cos Y - 1 )} X ду

Применение преобразования Лапласа по безразмерному времени 6 переводит (4)-(6) в систему для изображения

sh]B ²у ² + A² д ² + s ( x - 1 ) s * sh ( 2 д/ B ²у² + A ² д² + s )

T l ( X , Y , Z , s ) = L ^{- 1} [ T ( X , Y , Z, 0 ) ]

d + A 2 d + B 2 d = sT_L ;

д X ²       д Y ²       д Z ²      L

T l (0, Y , Z , s ) = s ;

T l (1, Y , Z , s ) = T l ( X ,0, Z , s ) = T l ( X ,1, Z , s ) = = T l ( X , Y ,0, s ) = T l ( X , Y ,1, s ) = 0.

Применим обратное преобразование Лапласа. Для этого воспользуемся теоремой Ващенко-Захарченко [2]:

L ^{- 1}

^ ^{( X} , д , Y , s ) "I = ^ ( X ₁ д ₁ Z ₂0 ) _ ^ ⁽ д , у , s ) J     ^ ⁽ д , у ^{,0 )}

+ £ ^{y (} X ■ ^{д , у} ' s ; ) X exp ( s , e ) k = 1 ^ ⁽ д , Y , s ; )

+

L

В нашем случае:

ф(X , m , Y,s )      2 ( cos m - 1 )( cos у - 1 )

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_                    ^^^^^^* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™

^^^^^^е

X

где P_k - корень уравнения sin p_k = 0. Переходя последовательно к оригиналу в (17), получим окончательное решение (рисунок 1):

MY

( cos M m ^- 1 )( ^cos Y n ^- 1 )

X

+ sh (2 л/ B 2y

Pk sin

P k sin

X k=1

x exp

^X sin ( M m^Y )^X sin ( Y n^Z )

M m Y n

+ 2 ^ ( в _к ² + 4 B 2 Y 2 + 4 A ² M ² ) cos P _k

+2^^ ( Pk ² + 4 B ² y ² + 4 A² m ²) cos p_t

W CO

T (X, Y, Z ,e) = -8^Z m=1 n=1

_ v( m , Y , s ) _

I shjB ² у ² + A ² m ² ( x - 1 )

k = 1

x exp

■² + A² m ²)

P k ( X - 1 )

sh P B 2Y ² + A ² m ² ( x - 1 ) sh ( 2 PB ² y ² + A ² m ² )

Pi.

B ² y ² - A ² M

- Pk- - B 2 Y ² - A ² M

-

-

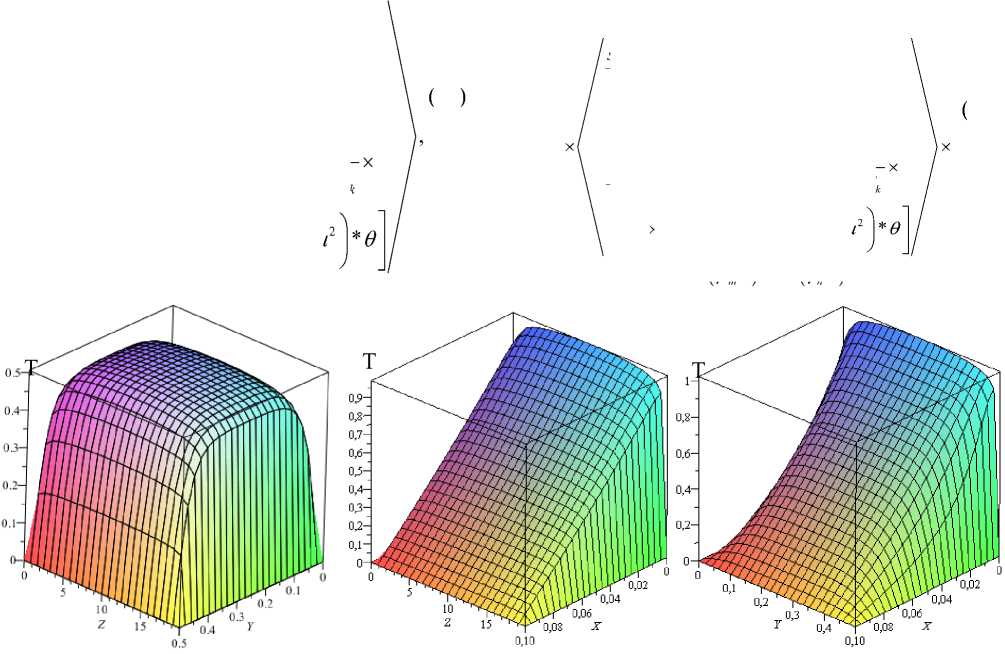
(a)

(b)

фиксированных значениях

Рисунок

Распределение температур

(c)

h 1 = 0,1; h 2 = 0,5; h 3 = 20; e = 1 и: a)

P_k ( x - 1 )

при

X = 0,05; b) Y = 0,25; c) Z = 0,25

Figure 1. Temperature distribution at fixed values h 1 = 0,1; h ₂ = 0,5; h 3 = 20; e = 1 и: a) X = 0,05; b) Y = 0,25; c) Z = 0,25

Заключение

В работе продемонстрировано применение конечного-интегрального преобразования для получения решения поставленной задачи новой структуры.