Нестационарные эффекты в математической модели роста тромбоцитарного тромба

RUSSIAN JOURNAL OF BIOMECHANICS

кровотока и могут провоцировать инфаркты и инсульты. Тромбообразование может сопровождаться об-

Нарушения свертывания крови часто лежат в ос-

разованием эмболов и вызывать закупорку сосудов нове других сердечно-сосудистых заболеваний. В част-       даже вдали от места их повреждения. Образование ности, артериальные тромбы приводят к нарушению       тромбов в организме происходит различными

0000-0002-0985-6409

0009-0006-6752-3668

0000-0003-0391-3289

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

способами. Так, в крупных артериях при больших скоростях течения крови и больших напряжениях сдвига, как правило, растут белые (тромбоцитарные) тромбы [1]. В [1] обсуждаются детали образования белых тромбов при патологически высоких напряжениях сдвига. Основным материалом белого тромба являются тромбоциты. В артериальной системе при тромбозе к тромбу прикрепляются миллионы активированных тромбоцитов за время порядка 10 мин.

В венах процесс роста тромба обусловлен наработкой и последующей полимеризацией фибрина. При этом важную роль играют тромбоциты, так как многие процессы происходят именно на мембранах активированных тромбоцитов [2; 3]. Существуют математические модели роста сгустка в сосуде с учетом накопления и адгезии тромбоцитов [4]. Отметим, что именно математическая модель [4] лежит в основе упрощенных (феноменологических) математических моделей тромбозов и роста сгустков. Например, на основе упрощения математического описания агрегации тромбоцитов построена модель [5; 6].

При математическом моделировании роста тромбоцитарных тромбов часто используются квазистацио-нарные математические модели с осреднением скорости кровотока по времени.

Первоначально подход с осреднением скорости по времени был применен для моделирования роста тромба в венах [7; 8]. Для производства тромбина использовалась упрощенная феноменологическая модель. Также упрощенно учитывался фазовый переход – образование фибрин-полимера.

Так как белые тромбы формируются главным образом в артериальном дереве, где процессы носят существенно нестационарный характер, исследование эффектов, проявляющихся в нестационарном течении, представляется актуальным.

Математические модели роста тромбоцитарного тромба используют следующие основные подходы:

• 1.    Многомасштабные (или мультифизические) модели. Кровь в таких моделях рассматривается как сплошная среда, а форменные элементы (тромбоциты, эритроциты) – как отдельные частицы. Примерами моделей такого типа являются [9–12].

• 2.    Упрощенные математические модели типа «реакция – диффузия – конвекция». Хотя концентрация тромбоцитов в крови сравнительно невелика (250 000– 400 000 ед./мкл), и для таких концентраций корректность использования диффузионных уравнений под вопросом, такие модели развиваются. Простая диффузионная модель формирования тромбоцитарного тромба предложена в [16]. Развитие модели и расчеты роста тромба в стационарных потоках описаны в [17].

В [9; 10] форменные элементы крови (тромбоциты, эритроциты) рассматриваются как деформируемые объекты, учитываются силы, действующие на них со стороны жидкости. Конечно, такие подходы формально позволяют учесть множество эффектов, но требуют чрезвычайно большого объема вычислительных ресурсов.

В [12] на основе подхода мультимасштабного моделирования учитывалась, например, кальциевая регуляция при активации тромбоцитов.

Сочетание методов механики сплошных сред для описания движения крови и методов частиц для описания движения и агрегации тромбоцитов использованы в моделях «виртуальных тромбоциитов [13]. Заметим, что для этих математических моделей характерна зависимость скорости агрегации частиц от скорости сдвига течения. Модель «виртуальных тромбоцитов» далее была использована авторами для моделирования роста тромбоцитарных тромбов при наличии стентов, в частности, при учете дефектов материала стентов [14].

Другой пример сочетания разных методов для описания движения жидкости и движения тромбоцитов использован в [15]. Для описания течений применен метод решеточных уравнений Больцмана, а для движения и агрегации тромбоцитов ― методы частиц (лагранжевой динамики). Метод решеточных уравнений Больцмана менее затратен, чем решение многомерных уравнений механики сплошной среды, но дает лишь качественные характеристики течения. Такое сочетание позволило авторам [15] описать процесс активации тромбоцитов при активации фактора фон Виллебранда.

Отметим, что использование математических моделей сплошных сред, в частности диффузионной модели, позволяет сильно снизить требования к использованию ресурсов компьютера при моделировании. Однако такое описание не может иметь физического обоснования ввиду малых концентраций тромбоцитов (примерно 300 000 ед./млл). Тем не менее такое упрощенное описание позволяет исследовать некоторые характерные черты математических моделей формирования тромбоцитарных тромбов в потоках жидкости.

Материалы и методы

Математическая модель переноса и агрегации тромбоцитов

При росте белого тромба существенную роль играет динамика агрегации тромбоцитов. Во многих работах для описания переноса и активации тромбоцитов применяются уравнения типа «реакция – диффузия – конвекция». При расчетах использовалась математическая модель [18]. Для эволюции концентрации тромбоцитов в модели рассматривались модифицированные уравнения [5; 6]. С учетом зависимости подвижности тромбоцитов от напряжения сдвига уравнения для концентрации тромбоцитов записаны в следующем виде:

d C„,

• -+- + div ( v C pi ) = - div ( - D pi grad C pi ) - Q , (1)

и для активных тромбоцитов

C P- + div ( v C _AP ) = - div ( - D _Pl grad C _AP ) + Q .   (2)

Здесь Q описывает переход тромбоцитов в активированное состояние. Для Q использовалась оценка [19]:

Q = k pi C pi C AP + k II _a C pi II _a .              (3)

В (1)–(3) использованы обозначения: k _pl – коэффициент активации тромбоцитов, C _pl – концентрация пассивных тромбоцитов, C _AP – концентрация активных тромбоцитов, k_na - скорость активации тромбоцита тромбином, II _a - концентрация тромбина, D _Pl – эффективный коэффициент диффузии тромбоцитов, υ – скорость тока крови.

Коэффициент диффузии тромбоцитов определяется как собственной подвижностью (броуновским движением), так и подвижностью за счет взаимодействия частиц большого размера в сдвиговом потоке. Упрощенные оценки влияния сдвига на транспорт тромбоцита приведены в [16]. Броуновским движением тромбоцита в [16] пренебрегалось.

В [5; 6] для подвижности тромбоцитов принято

D _PL = 1,9-10 ^{- 13} + 7-10 ^{- 13} 1 2 м²с^-1.

Первое слагаемое здесь описывает собственную подвижность тромбоцитов (броуновское движение), второе – транспорт частиц в сдвиговом потоке, который зависит от второго (квадратичного) инварианта тензора скоростей деформации:

I 2 = | ^ 22 S 33 - S 32 S 23 ⁺ S 11 S 33 - S 31 S 13 ⁺ S 11 S 22 - S 21 S 12 I ^.

полная активация тромбоцитов и расщепление фибриногена до фибрина.

При таком использовании массовых долей вместо концентраций возникает размерный коэффициент перехода в (3а), связанный с массой единичного тромбоцита. Конечно, in vivo тромбоциты имеют различные характеристики, зависящие, например, от возраста тромбоцита. Для нашей модели принималось приближение   «среднего тромбоцита» с массой:

М PL = М AP = 5 • 10-15 (кг). В этом случае коэффициент в (3а) KPL = 3010 .

Производство тромбина в сосуде описывалось уравнением

• + ( v V)II a =- d iv (_ D grad II a ) + k⁹^ XI a .   ⁽⁵⁾

d t                                        h 9 h y о

Константы скоростей реакций, входящие в (5), следующие: k 2 – скорость активации тромбина под действием фактора Xa, k 9 – скорость реакции активации фактора IX, k 10 – скорость реакции активации фактора X под действием IX a , h 9 – скорость утечки фактора IX a , h 10 – скорость утечки фактора X a . По данным [21], при оценке констант, входящих в (5), имеем

2 = 0,15 с -¹. h ₉ h ₁₀

Заметим, что прималых концентрациях тромбина скорость его производства зависит от концентрации активной формы фактора XI. Важность учета фактора XI подчеркивалась в [22].

Для связи с пакетом FliowVision это уравнение удобнее формулировать в терминах массовых долей

5 = ij

1 f d V  3 V j ^

- —- + —-

Ч⁵ x j   ^d x i J

^PV^{2 + V} ( ^{v PV} 2 ) ^{+ V} ( ^{_ D VpV} 2 ) = ^kII ^pV pro       (7)

Так как используемое для расчетов ПО FlowVision применяет в качестве основных переменных массовые доли, то при переходе к массовым долям уравнения переходят в dpVPl + div(vpVpl) = _div(_DPlgradpvPl)-KptQ,   (^a)

^^^ + div ( v p_V AP ) = _ div (_ D Pl grad pv AP ) + K_plQ ,    (2a )

В правой части (7) стоит массовая доля протромбина pv _pro . Коэффициент диффузии совпадает с коэффициентом диффузии тромбина.

В [5; 6] предполагается, что формирование тромба происходит также под действием некоторого свертывающего фактора, выделяющегося из активированных тромбоцитов. Известно (работы по фактору V), что при активации тромбоцитов выделяется частично активированный фактор V (акцелерин) [23]. Тогда для него можно записать уравнение kPl Pv pl Pv AP   kIIa pv pl  pv2            (3 a)

^K pl          K pl   P ^V 2 Cr

^PV^{5 + V} ( ^v pv₅ ) ^{+ V} ( ^_ D RT ^V pv₅ ) = a f m^Spl .    (8)

Здесь pv Pl - массовая доля пассивных тромбоцитов, pv₂ - массовая доля тромбина, pv_{2 Cr} - критическая массовая доля тромбина. Мы полагали ее соответствующей концентрации тромбина 10 нмоль/л. По данным [20], при концентрации от 10 до 30 нмоль/л происходит

Здесь v5 - массовая доля акцелерина, Def - эффективный коэффициент диффузии (м2с-1), D0 – опорный коэффициент диффузии (м2с-1), I2 - второй инвариант тензора скоростей деформации (с"2), I2 Cr критическое значение квадратного корня из второго инварианта (с-1), fM - переводной коэффициент (кг),

S PL — объёмный источник (м^-3с^-1), определяемый равенством (3 а ).

В [5] предполагалось, что коэффициент диффузии равен

Ι² 2

D eff =       D 0^Do                 ⁽⁹⁾

Ι² 2 Cr +Ι² 2

В (8) а — коэффициент, определяющий степень активации фактора V. По оценкам [24], это значение около 0,5.

Числовые значения:

1 2 Cr = 90 . 120 (с^-1),

D = 10-12 -10-11 (м2 с-1), а = 0,5-0,95 , fM = 1,9565 -10-9 (кг).

Рост тромба в модели описывается уравнением адсорбции активных тромбоцитов на доступной поверхности

∂Y m =-Рdplф -^P(кг м-2 c-1).           (10)

∂ n

V

Величина ф =----a---, введенная в рассмотре-Va,Cr + Va ние в [5; 6], в рамках настоящей модели может трактоваться как некоторый коэффициент эффективности адсорбции, связанный с производством фибрина, необходимого для скрепления активных тромбоцитов с тромбом. В силу постоянства плотности крови выражение для φ, входящее в (10), можно переписать в эквивалентной форме с использованием массовых долей ф        pv5      .

ρν _{5, Cr} +ρν ₅

Массовая доля фактора V тогда будет определяться уравнением (8).

Константа в знаменателе последнего уравнения в этом случае будет трактоваться как постоянная Михаэлиса для реакции производства фактора V , ее значение по данным [25] 5,09 ^ 10^-9 (кгм^-3).

Математическая модель движения крови, начальные и граничные условия для уравнений математической модели

Для определения поля скоростей жидкости в области с подвижной границей фазового перехода решались уравнения Навье — Стокса (для приближения ньютоновской жидкости). Для потока жидкости во всех расчетах на входе в сосуд задавалась скорость потока жидкости, на выходе — давление. Использовалась интерполяция соответствующих экспериментальных зависимостей от времени.

Для некоторых вариантов рассчитывалось течение неньютоновской жидкости. Использовалось приближение эффективной вязкости.

На стенках сосуда и на поверхности растущего тромба использовалось условие прилипания, скорость течения на стенке равна нулю.

Для тромбина во входном сечении задается нулевая концентрация. На стенках сосуда использовано условие непроницаемости — полный поток тромбина на стенке, складывающийся из диффузионного и конвективного, равен нулю. На выходе поставлено свободное граничное условие — образовавшийся тромбин уносится потоком жидкости.

Для тромбоцитов во входном сечении в зависимости от расчетов задавалась либо постоянная массовая доля, либо распределение массовой доли в зависимости от расстояния от стенки. На поверхности стенки и тромба диффузионный поток тромбоцитов в нормальном направлении равен нулю. На выходе поставлено свободное граничное условие — тромбоциты уносятся потоком жидкости.

Для активных тромбоцитов во входном сечении их массовая доля равна нулю. На поверхности стенки, недоступной для роста тромба, диффузионный поток активных тромбоцитов в нормальном направлении равен нулю. На доступной поверхности сосуда и на поверхности тромба нормальная составляющая потока тромбоцитов определяется выражением (10). На выходе поставлено свободное граничное условие — активированные тромбоциты уносятся потоком жидкости.

Методы и программное обеспечение

Для совместного расчета задач гемодинамики, «конвекции — реакции — диффузии» и фазового перехода при росте тромба использован программный комплекс FlowVision . Программный комплекс FlowVision [26] основан на конечно-объемном подходе к аппроксимации уравнений движения жидкости и газа. Используется автоматическое построение расчетной сетки. Расчетная сетка вдали от границ является декартовой, однако около границ она превращается в неструктурированную сетку, имеющую в качестве ячеек произвольные многогранники. Расчетная сетка адаптируется к геометрическим особенностям и к решению локально и динамически.

Для отслеживания перемещения контактных границ, разделяющих несмешиваемые жидкости, применяется усовершенствованный метод VOF [27], в котором используется подсеточное разрешение объемов жидкости, размер которых меньше размеров расчетных ячеек. Это позволяет добиться консервативности метода VOF .

Верификация FlowVision для задач гемодинамики проводилась на задачах FDA о сопле и насосе для

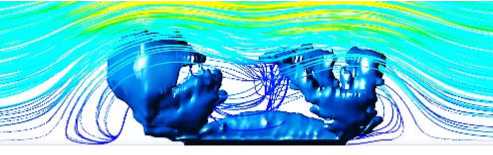
Рис. 1. Модуль скорости крови и линии тока возле растущего тромба

Расчетные случаи

№ п/п	ЧСС, уд./мин	Продолжительность систолы, с
1	83	0,33
2	120	0,23
3	300	0,09

перекачки крови [28; 29]. Результаты верификационных расчетов описаны в [30; 31].

Результаты расчетов

Формирование тромбоцитарного тромба в артериоле кремастера мыши

Для решения первой задачи рассматривалось течение в цилиндрической трубке длиной 2 мм. На стенке сосуда имелась поврежденная область с характерным размером 20 или 50 мкм. На входе сосуда задавалась объемная скорость потока, зависимость скорости от времени представляла собой интерполяцию по литературным данным. На выходе сосуда задавалось давление. Расчет проводился для разных частот сердечных сокращений (ЧСС). Также проводились расчеты с осредненной по времени скоростью. Считалось, что содержание тромбоцитов 300 000 ед./мкл.

Проводились расчеты для случая идеальной жидкости и для модели вязкости Берда ‒ Каро:

n - 1

H=H min + ( ^ max — ^ min ) ( 1 + ^ S ) 2 ,

S = 2%^, i,j где Sij определяются равенством (4).

Для модели Берда – Каро использовались следующие параметры [32]:

μ min = 0,0032 – минимальная вязкость (Па с);

μ max = 0,0456 – максимальная вязкость (Па с);

λ = 10,03 – коэффициент релаксации (с); n = 0,344 – эмпирическая постоянная.

В рамках исследования было рассмотрено несколько расчетных случаев с разной частотой сердечных сокращений (ЧСС). В таблице приведены основные сведения по расчетным случаям.

Во всех расчетах на входе в артериолу задавалась скорость жидкости в зависимости от времени, на выходе – нулевое давление. Максимальное значение линейной скорости в артериоле равнялось 0,003 м/с для всех вариантов.

На поверхностях артериолы и растущего тромба устанавливались условия прилипания: скорость течения на этих границах равнялась нулю. Предполагалось, что тромб растет достаточно медленно, возмущения скорости, вызванные ростом тромба в нормальном к скорости направлении, быстро затухают.

Для модели Каро и модели идеальной жидкости получены качественно схожие результаты. Ниже приводятся иллюстрации для расчетов по модели Берда ‒ Каро.

На рис. 1 для частоты сердечных сокращений 120 уд./мин показано распределение абсолютной величины скорости и линии тока в фазу систолы.

Видно, что перед проксимальной частью растущего тромба, преграждающего путь набегающему потоку крови, формируется небольшая зона возвратного течения. В ней происходит наработка тромбина. Выход тромбина за пределы зоны возвратного течения приводит к активации тромбоцитов.

Заметим, что основной рост тромба происходит именно в фазу систолы – увеличивается подвижность тромбоцитов в соответствии с (1), (2). Максимальное значение скорости сдвига соответствует наибольшей густоте линий тока на рис. 1.

Это объясняет типовой сценарий роста тромба. При формировании препятствия в потоке именно около него повышается подвижность тромбоцитов. Неоднородность начинает расти в направлении, перпендикулярном скорости потока. Возникает неустойчивость, приводящая к образованию структур типа «столбов».

Так как подвижность тромбоцитов является функцией времени, близкой к периодической, то интерес представляет исследование закономерностей роста сгустка в зависимости от частоты сердечных сокращений.

На рис. 2 приведены цветовые карты распределения тромбина для времени 180 с и размера повреждения 20 мкм для различной частоты сердечных сокращений. Темно-синим цветом показан растущий тромб.

Максимальная концентрация тромбина для всех вариантов достигается в области перед тромбом. В случаях ЧСС 83 и 120 уд./мин (физиологическая норма) тромб интенсивно растет по краям поврежденного участка. При этом тромбоциты прикрепляются преимущественно к той части поврежденного участка, которая расположена выше по течению (проксимальнее). В боковых частях тромба образуются «стенки», во внутренней части тромба высота меньше. Для случая с частотой сердечных сокращений 300 уд./мин происходит формирование фрактальной структуры во всех частях тромба, при этом более интенсивный рост наблюдается проксимальнее повреждения.

Расчет формирования тромбоцитарного сгустка в воротной вене человека

Для моделирования роста тромба в воротной вене в качестве расчетной области бралась 3 D -рекон-струкция фрагмента воротной вены по данным КТ. В качестве расчетной области выбирался изогнутый фрагмент вены длиной около 15 см переменного сечения с диаметром от 0,6 до 1,3 см до разветвления на левую и правую воротные вены.

Для задания скорости на входе воротной вены использовались данные УЗИ пациентов [33]. Предполагается, что существенная зависимость скорости венозного кровотока в данной задаче может быть связана как с пульсовыми волнами, так и с частотой дыхания. В отличие от течения крови в кремастере мыши, в течение одного дыхательного цикла наблюдается и фаза с прямым током крови, и фаза противотока.

Максимальная скорость крови в фазе с прямым током достигает 51 см/с, а максимальная скорость противотока 20 см/с. Средняя скорость крови в вене 27 см/с. Экспериментальная кривая заменялась ее кусочно-линейной интерполяцией.

Кроме того, в данном случае полагалось, что у пациента тромбоцитопения, содержание тромбоцитов для расчетов предполагалось 100 000 ед./мкл.

На выходе из воротной вены ставилось условие постоянного (нулевого) давления. Хотя граничные условия в выходных сечениях оказывают существенное влияние на характер нестационарных течений [34], для постановки корректных граничных условий для задачи о воротной вене нужна математическая модель функционирования печени. Граничные условия типа виндкесселя в данном случае неприменимы.

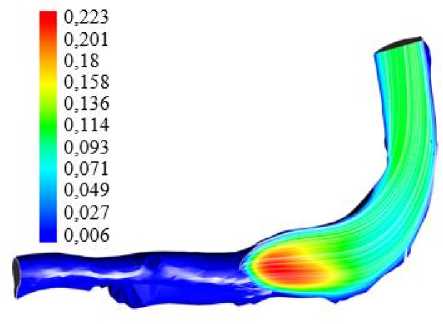
Ниже приведены иллюстрации для модели ньютоновской жидкости с плотностью 1050 кг/м³ и вязкостью 0,003 кг/(м · с). На рис. 3 приведены распределения абсолютного значения скорости кровотока и линий тока в воротной вене. Распределения приведены лишь для фазы прямого тока крови (по направлению к печени). На рис. 4 показаны расчетные зависимости завихренности для максимальной и минимальной скорости прямого кровотока. Заметим, что в фазе реверсивного тока значения завихренности и скорости сдвига существенно меньше, чем для прямого тока.

Видно, что характер течения в вене существенно сложнее, чем для задачи о росте тромба в артериоле.

Рост тромба происходит в основном в фазе прямого тока; для этой фазы течения характерны большие (по сравнению с фазой реверсивного тока) значения

а

p-14 ■ 1.805e-14

1.61e-14

1.415e-14 1.22-14 L025e-14 8.3e-15 6.35e-15

I 4;4e-15 ■ 2.45e-l?

I 5e-15

б

в

Рис. 2. Распределение тромбина с учетом пульсовых волн: а – частота сердечных сокращений 83 уд./мин; б – частота сердечных сокращений 120 уд./мин; в – частота сердечных сокращений 300 уд./мин завихренности и скорости сдвига. Фаза обратного кровотока позволяет части активированных тромбоцитов «вернуться» к поврежденному участку сосудистого эндотелия.

Для моделирования роста тромбоцитарного сгустка предполагалось, что имеется поврежденный участок эндотелия, доступный для активированных тромбоцитов. Область поврежденного эндотелия в приведенном расчете располагалась в районе изгиба воротной вены в зоне, где во всех фазах течения скорость потока крови минимальна. Зона повреждения была сложной формы, ее площадь составляла примерно 30–35 мкм. Форма тромба для частоты колебаний скорости 60 колебаний в минуту приведена на рис. 5.

Видно, что в этом случае структуры («столбы»), перпендикулярные местной скорости потока, формируются на всей доступной для тромбоцитов поверхности. Изменение частоты колебаний скорости приводит к сглаживанию формы растущего тромба.

Заметим, что для задачи поиска «фрактальных» структур в модели роста тромба большое значение играет выбор модельного «места повреждения» эндотелия – поверхности сосуда, доступной для прикрепления тромбоцитов.

Рис. 5. Форма растущего тромба в воротной вене при частоте сердечных сокращений 60 уд./мин

а

Рис. 3. Модуль скорости и линии тока в воротной вене в фазе максимума скорости потока ( а ) и минимума скорости потока ( б ) в сечении воротной вены плоскостью, проходящей через область

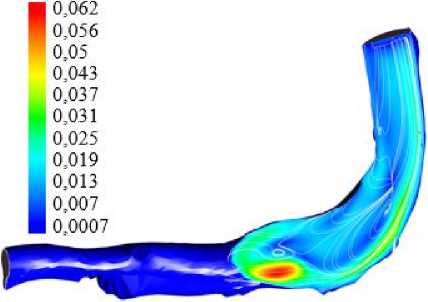
б

повреждения эндотелия

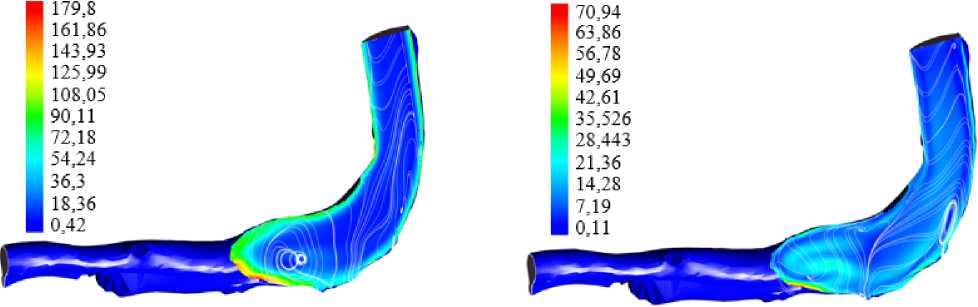
б

Рис. 4. Распределение завихренности в воротной вене в фазе максимума скорости потока ( а ) и минимума скорости потока ( б ) в сечении воротной вены плоскостью, проходящей через область повреждения эндотелия

Заключение

Для двух задач результаты получились схожими: существует такое значение частоты изменения скорости потока (сердечных сокращений для задачи об артериоле кремастера, колебаний скорости кровотока для воротной вены), при котором формируется тромб со сложной поверхностью фрактального типа. При небольшом сдвиге ЧСС происходит смена характера роста тромба, его поверхность становится гладкой.

Проведенные расчеты находятся в хорошем соответствии с экспериментальными исследованиями формирования тромба в артериолах кремастера мыши [35]. На основе проведенных расчетов показано, что характер роста тромба может резко меняться в зависимости от ЧСС. Ввиду того, что в математической модели не учтено взаимодействие растущей структуры с эритроцитами, скорее всего, фрактальный характер тромба является характерной чертой лишь данной математической модели. Кроме того, математическая модель не учитывает возможность отрыва тромбоцитарного агрегата с поверхности растущего тромба. Предполагается, что процесс прикрепления тромбоцита к растущему сгустку является необратимым. Экспериментальные данные показывают, что необратимо тромбоциты связываются со сгустком с помощью полимеризовавшегося фибрина. Таким образом, для построения корректной математической модели явления необходим учет активации фибриногена до фибрина и описание полимеризации фибрина. В обзоре [36] отмечается, что внешняя часть растущего тромба обладает рядом особенностей: в связи с низким уровнем активации          Исследование нестационарных эффектов при росте тромбоцитов и минимальной активностью тромбина       тромбоцитарных тромбов может быть полезно при чис- данная область тромба, которую часто называют обо-       ленном исследовании тромботических осложнений при лочкой (англ. shell), обладает высокой подвижностью;       хирургических операциях. Течение в зоне анастомоза в динамичность внешних слоев тромба в условиях по-       персонифицированных моделях существенно зависит тока может существенно влиять на его размер, однако       от структуры и расположения анастомоза [37]. Если об- адекватное описание физики взаимодействия потока с       ласть анастомоза совпадет с зоной ускоренного формитакой динамичной структурой требует использования       рования тромбоцитарного тромба, то риск тромботиче- соответствующих вычислительно сложных моделей.         ских осложнений возрастает.

Неочевидно, каким именно образом эффекты не-          Вопрос об оценке резонансных частот для каждого стационарности потока способны проявиться в буду-       конкретного пациента остается открытым. По-види- щих сложных математических моделях.                     мому, он должен решаться на основе эксперементаль- ного исследования тромбоза и гемостаза.