Нестационарные тепловая и диффузионная задачи для катодных узлов сильноточных плазменных систем

Экспериментально установлено [1, 2], что при давлении рабочей среды p > 10 ⁵ Па в сильноточных плазменных устройствах получить достаточный эмиссионный ток при использовании катода из тугоплавкого металла удается только при температуре, превышающей температуру его плавления. Введение эмиссионных активаторов в виде окислов редкоземельных элементов в объем основного металла [3], снижающих его работу выхода электронов, приводит к уменьшению необходимой рабочей температуры при тех же плотностях тока и, соответственно, тепловой нагрузки на катод. В процессе работы в материале таких электродов происходит диссоциация окислов легирующего металла с последующим растворением в матрице основы и диффузией их к поверхности. При этом на поверхности катода образуется пленка испаряющихся атомов активирующего элемента [2]. Для обеспечения устойчивой работы катодов в течение длительного времени необходимо поддержание постоянного баланса частиц, испаряющихся с рабочей поверхности и подводимых диффузией из внутренних объемов. Динамика этих процессов и интенсивность выхода активаторов из объема матрицы основного металла определяют работоспособность и ресурс данного класса электродов [4]. Поэтому для оптимизации их функциональных режимов необходимо исследование закономерностей электро- и тепломассопереноса в зависимости от внешних параметров (разрядный ток, геометрия, конструкция и материал катодного узла, давление и род плазмообразующего газа и др.) плазменных устройств.

В данной работе для исследования этих процессов в единой постановке рассматриваются нелинейные тепловая и диффузионная задачи применительно к катодным узлам сильноточных плазменных систем.

Постановка обобщенной задачи

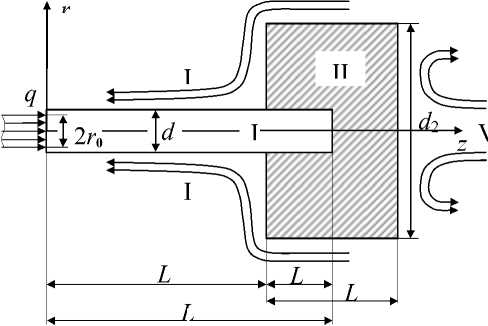
На рисунке 1 представлена модель типичного катодного узла плазменных устройств. Для сильноточных электродуговых систем наиболее работоспособными являются конструкции, состоящие из стержневого электрода – вставки I из тугоплавкого металла (например, из чистого или активированного вольфрама), запрессованного в медный цилиндрический корпус держателя – обойму II [1]. Длина вылета катода из обоймы варьируется от L c = 0 (заделка заподлицо) до L c / d 1 >> 1 (длинный катод).

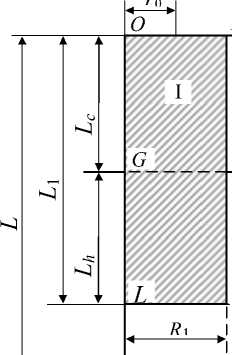
В расчетной схеме (на рисунке 2 показана полуплоскость осевого сечения модели) на рабочий торец стержневого термоэмиссионного катода I ( z = 0) в пределах круга радиуса r 0 поступает осесимметричный тепловой поток, моделирующий термическое воздействие плазмы разряда: q 0 = F ( r ), где F ( r ) – в общем случае известная функция, r и z – цилиндрические координаты.

II

L

Рис. 1. Составной катодный узел плазменных устройств. I - катод (вставка), II - корпус держателя (обойма), III - плазма разряда, IV - плазмообразующий газ, V - теплоотвод (жидкость)

A i = 0

B i = Ni

KF

C

II

k = 0

i = N

k = M

______R2

E

r

k = M

z

Рис. 2. Расчетная схема катодного узла

Для исследования процессов электро- и тепломассопереноса активатора необходимо решить систему из трех нелинейных уравнений в двумерном приближении:

• а) уравнения теплопроводности

  д T

  
  

  1 д

  
  

  д T _

  
  

  д T _

  
  

  д T_k   1 д   . д T_k     д  . д T

  ^c k P k^T = - ^r ^ k^{( T} )^ k +^ ^ k^{( T} )^ k ⁺ J k ¹ ^ k^{( T );} д t   r д r д r     д z д z

  
  

  д t

  
  

  r д r

  
  

  б) уравнения непрерывности тока

  1 5 Г

  - IT r ^ k ( T ) r д r

  
  

  Jk = ( Jr + Л ^²,

  
  

  д r

  
  

  д U_k д r

  
  

  J_r = -n k ( T ) д U I д r ,

  
  

  д z

  
  

  д

  + 8 z ' k ^{( T} )

  
  

  д U k д z

  
  

  = 0

  
  

  J z = -Q k ( T ) д U k I д z

  
  

  ;

  
  
  
  
  
  

  для вставки ( k = 1) и обоймы ( k = 2);

  д n 1 д

  в) уравнения диффузии для катода — =--

  д t r д r

  
  

  д n д ^^д n ^{rD ( T} )— +— D ^{( T} )— , д r д z       д z

  
  

  д n

  
  

  д r

  
  

  д

  
  

  д z

  
  

D ( T ) = D o exp( - Q^ ), kT

где T k - температура; c k , р _к , X _к , о _k - соответственно удельная теплоемкость, плотность, коэффициент теплопроводности, удельная электрическая проводимость материалов катодного узла; j k - плотность тока; U k - потенциал электрического поля; n , D , D о , Q a , - соответственно концентрация, коэффициент диффузии, фактор диффузии, энергия активации легирующего элемента (присадки); к -постоянная Больцмана; t - время.

Граничные условия к уравнению (1) поставлены следующим образом:

• 1)    на рабочем торце вставки (поверхность ОА на рис. 2) реализуются теплоперенос из дугового разряда на катод, теплообмен с газовой средой и излучение по закону Стефана- Больцмана:

.   ) dT1(r,0) J"qо, 0 < r < ro dz     \ag(T -Tg) + ^T)aB(T -Tg4), ro < r < R;

• 2)    на горячем торце держателя ( ВС) происходит теплообмен с газом:

X 2 ( T ) ° _ , ^c ) = a g ( T ₂ - T g ),    R i <  r <  R 2 ;

dz

• 3)    холодный торец держателя ( KE) охлаждается жидкостью:

X 2 ( T ) ^{8 T} ( ^r ’ L ) = -a f (T , - T, ) , 0 <  r <  R 2 ; d z

• 4)    на цилиндрических поверхностях вставки ( АВ ) и держателя ( СЕ) осуществляются конвективный теплообмен и излучение по закону Стефана-Больцмана:

X i ( T ) ^{9T 1(} R ^1, z ) = -a g ( T - T g ) -8 1 ( T ) о в ( T i⁴ - T g ⁴), 0 <  z <  L_c ,

Оr          6       6

X 2 ( T ) ^{5 T} 2 ⁽ R^z ) =-a g ( T 2 - T g ), L c <  z <  L ; d r

• 5)    на оси симметрии катодного узла ( OK) радиальный тепловой поток равен нулю: ^{5 T} k ^(0, z ) = 0, 0 <  z <  L .

5 r

Уравнение (2) решается для катода с граничными условиями:

• 1)    на рабочем торце катода ( OA ):

  ^ (t ) d U i C r ^P) = J

  ^1V ’    d z

  
  

  —I— , 0 <  r <  r0 ^r)

  
  

  0, r <  r <  R i ;

  
  

• 2)    на холодном торце ( LH):

U i ( r , L i ) = 0, 0 <  r <  R i ;

• 3)    на цилиндрической поверхности ( AH ):

5 U i ( R i , z )

= 0, 0 <  z <  L_c ,

5 r

U i ( R i , z ) = 0, L_c <  z <  L i ;

• 4)    на оси катода ( OL ):

5^ = 0, 0

5 r                       ¹

Здесь приняты следующие обозначения: I - разрядный ток; о_в - постоянная Стефана-Больцмана; 8_к(T) -степень черноты; a_g, a,- коэффициенты теплоотдачи газу и жидкости; T_g, T, - температуры газа и жидкости.

Краевые условия к уравнению (3) сформулированы в виде:

• 1)    в начальный момент времени концентрация присадки в катоде считается распределенной равномерно и равной

n (r, z, 0) = n0;

• 2)    на холодном торце катода (LH) концентрация остается постоянной

n ( r, L i, t) = n о,       0 < r < R1;

• 3)    на горячем торце катода (OA) происходит испарение присадки и возврат ее из приэлектродной области в пределах контакта с разрядом - круга радиуса r₀:

• - D₍T) 3n(r,0, t)   1(1 — П )(n I nm )²'³ W(T ), ⁰< r< -c

az       ( (n I nm i WlT),      r0 < r < Ri, где nm - концентрация частиц основного металла (матрицы) катода; коэффициент n' nm/3 учитывает различие поверхностных и объемных концентраций присадки; п — доля ее атомов, возвратившихся на поверхность катода за счет рециклинга из приэлектродной области; W(T) - скорость испарения присадки;

• 4)    радиальный поток на оси симметрии катода (OL) равен нулю:

⁹n^(0,z’ t) = 0, 0 < z< L ;

5z

• 5)    граничное условие на цилиндрической поверхности (AH):

5 n(Rz, t)

0 < z < Lc

Lc< z< Li-

• ^-D^(T)------ = ⁽n ' nm ) ^W(T),

оr

5 n (R", z, t)= 0

5 r’

Рассмотрим подробнее граничное условие в месте контакта дуги с катодом. Выбор продиктован следующими соображениями. Испарившиеся атомы металла, попадая в приэлектродную область, легко ионизируются электронами, так как вероятность ионизации металла больше вероятности ионизации 2

рабочего газа. При этом соотношение р'а - ne ' n^ (в, а - скорости ионизации и рекомбинации; n_e⁰, n_a⁰- равновесные концентрации электронов и атомов соответственно) больше для металла с меньшим Vi, что приводит к увеличению скорости избыточной ионизации атомов присадки по сравнению с атомами основного металла и рабочего газа . Под действием электрического поля ионы материала катода возвращаются обратно на поверхность, где восстанавливаются до атома. В результате этого скорость испарения в области пятна получается значительно ниже рассчитанной по температуре поверхности.

Явление рециклинга тяжелых частиц металла в прикатодной области дугового разряда экспериментально подтверждено в [5]. Заметим, что возврат ионов будет менее эффективным для катода, обдуваемого потоком газа, так как часть их выносится потоком из прикатодной зоны .

Скорость испарения в газовой среде записывается в виде:

w(T) = apps 1'(2пMRT) , где ps - давление насыщенных паров; М - молярная масса; ap - коэффициент испарения (Ленгмюра), который зависит от рельефа и чистоты поверхности катода, давления и рода рабочего газа. При атмосферном давлении в среде аргона и азота коэффициент ap принимается равным 0,01 - 0,05 [4].

Задачи электро- и тепломассопереноса в данной постановке аналитически не решаются. Поэтому используется численный метод конечных разностей с локально-одномерной схемой прогонки [6]. Метод позволяет корректно учесть такие факторы, как двумерность задачи, нелинейность граничных условий, зависимость тепло- и электрофизических свойств материалов от температуры и неравномерность распределения тока в объеме электрода. Область интегрирования I - II разбивалась на несколько простых областей (см. рис. 2) и смежные области «сшивались» едиными граничными условиями. Применены неявные двухслойные консервативные разностные схемы, где уравнения и граничные условия аппроксимируются со вторым порядком точности .

В дальнейших работах будут представлены методы решения задач и результаты численного моделирования.