Нестационарный изгиб консольно-закрепленной балки Бернулли-Эйлера с учетом диффузии

Эффекты взаимодействия полей разной физической природы, проявляющиеся в виде механодиффузии, термомеханодиффузии, электродиффузии, магнитодиффузии и другого, хорошо изучены экспериментально и широко используются в технике. Различные постановки и методы решения задач механодиффузии с возможным учетом других физических полей в последние десятилетия рассматривались в работах как отечественных, так и зарубежных авторов, что говорит об актуальности исследований в данной области [1–4].

С другой стороны, следует отметить, что подавляющее большинство публикаций связано с моделированием стационарных и нестационарных процессов в телах канонической формы: в слое или

полупространстве. В то же время реальные тела имеют конечный размер, поэтому наибольший практический интерес вызывают задачи механодиффузии в балках, пластинах и оболочках, являющихся основными элементами реальных конструкций.

Данной тематике посвящено сравнительно немного публикаций, среди которых можно отметить работу [5], в которой оценивается влияние диффузионных процессов на несущую способность пологой трансверсально-изотропной оболочки. Контактное взаимодействие стержня с упругим полупространством обсуждается в статьях [6, 7]. Публикации [8-10] содержат исследования механодиффузионных процессов в пластинах. Расчет сферических оболочек с учетом диффузии рассмотрен в [11].

В перечисленных работах механодиффузионные процессы являются стационарными, что полезно при изучении установившихся режимов работы различного рода механических систем. Для анализа кратковременных — импульсных — воздействий необходимо использовать нестационарные модели. Так, в публикациях [12-14] моделируются эффекты взаимодействия механического и диффузионного полей, вызванные нестационарным изгибом свободно опертых балок и пластин.

Как известно, граничные условия существенно влияют на подход к решению начально-краевой задачи и сложность его реализации. Например, условия свободного опирания позволяют строить решение в виде рядов по собственным функциям соответствующего упруго-диффузионного оператора. Для консольно-закрепленной балки, которая рассматривается в данной работе, получить такие функции не представляется возможным. В связи с этим применяется метод эквивалентных граничных условий. Суть метода заключается в переходе от исходной задачи к вспомогательной задаче для того же предмета исследования, но с граничными условиями, допускающими представление решения в виде рядов Фурье. Далее выводятся соотношения, связывающие правые части граничных условий для одинаковых параметров обеих задач. Они имеют вид интегральных уравнений Вольтерра 1 -го рода. Система этих уравнений решается численно, с помощью квадратурных формул.

• 2.    Постановка задачи

В работе рассматривается нестационарная задача упруго-диффузионного изгиба консольно-закрепленной однородной изотропной балки Бернулли-Эйлера при действии силы, приложенной к свободному концу (Рис. 1).

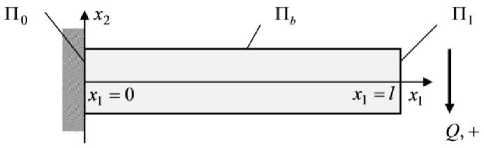
Рис. 1. Иллюстрации к постановке задачи: схема приложенных усилий ( а ) и ориентация координатных осей в поперечном сечении балки ( б)

а

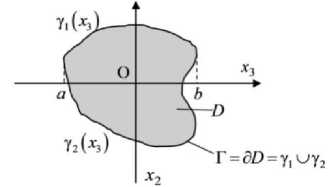
б

Для описания общего случая изгибного деформирования балки используется линейная модель упругодиффузионных процессов в сплошных средах в прямоугольной декартовой системе координат. Если деформируемая среда однородна, уравнения имеют вид [15-18]:

и,^ + F i ,    П ⁽ q ^- J - + Y ⁽ q ’    ( i , ^j = 1,3, q = 1, N ) ,                  (1)

dXj                  dx где точка над символом обозначает производную по времени, ау и J(q’ — компоненты тензора напряжений и вектора диффузионного потока, которые определяются следующим образом :

° -

= С

C jkl

^{д и}к ^{d x}l

N

- z « •• ’ л ¹ • ’ , q = 1

N                       ⁽ t ’

J ( q ’ -_У n( q Ы qt )£П_  .( q )

J = ^ D j g д_х +^ ijkl

^{d 2} u k

5 x_y 5 x,

( q = 1, N ) .

Все величины в (1) и (2) являются безразмерными:

*                     *                                               **

xiuiCt               Cijkl         2

=---, и, =---, Т =---, C =-----, C =----- l       1 l           l        jM   Cm1p

D *( q ’                m(q ’ D *( q ’a*( q ’ n(q ’

)(q ’ =   ij         л( q ’ = _________ij     kl 0         F = p l i        Y(q ’ j      Cl ’ jkl        pRT6Cl     ’     i   Сш! ’

a(q ’ a j lY,(q ’

C

a *^{( q} ’ ^a j

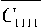
где в качестве характерных масштабов используются длина балки — l , и скорость волны растяжения-сжатия в упругой среде — C . Также приняты обозначения: t — время; x * — прямоугольные декартовы координаты; и * — компоненты вектора перемещений; n ^{( q} ’ = n ^{( q} ’ - n ( ^q ’ — приращение концентрации q -го вещества в составе многокомпонентной однородной среды; n О ^q ’ и n ^{( q} ’ — начальная и актуальная концентрации q -го вещества; Cу_Ы — компоненты тензора упругих постоянных; р — плотность среды; а * ( q ’ — коэффициенты, характеризующие объемное изменение среды за счет диффузии; D₍ * ^{( q} ’ — коэффициенты самодиффузии; R — универсальная газовая постоянная; Т_о — температура среды; m ( ^q ’ — молярная масса q -го вещества; F_t * — плотность массовых сил; Y * ( ^q ’ — плотность объемных источников массопереноса.

Уравнения (1) и (2) включают N независимых компонент, описывающих процесс деформирования многокомпонентной среды, состоящей из N + 1-го вещества. При этом приращение массовой доли N + 1 -го вещества выражается через приращения долей остальных N компонентов среды:

N n( N+1)=-2п( q’, q=1

что обеспечивает выполнение закона сохранения массы :

N + 1 ^ л ' ^q ’ = о.

q = 1

Начально-краевые условия относительно независимых записываются так:

компонент уравнений в общем виде

u - It= 0 = u - 0 , u.L o = ^V- 0 ,

n ⁽ q ’I = n O q ’ I t= 0

u ln = U i , u

n ^{( q} ’I = N ^{( q} ’ ,

1 1

° n L_o= P ^(t > ^{o )} ,

( i , j = 1,3, q = 1, N ) , d G =П и U П,

J ( ^q ’I    = I ( ^q ’   ( t> 0, q = 1, N ) , d G =П U n.

¹П J                V                          '

Здесь: d G — граница области решения задачи G ; n — компоненты единичного вектора внешней нормали к d G ; и ,₀, у ₀, n O q ’ — заданные функции пространственных координат. Далее полагается, что и,₀ = 0, v ,₀ = 0 , у ' ^q ’ = 0 . Величины, стоящие в правых частях граничных условий (5), есть поверхностные кинематические ( U , N ^{( q} ’ ) и динамические ( р , I ^{( q} ’ ) возмущения.

Для построения уравнений изгиба балки предпринимаются действия:

• -    осуществляется переход к вариационной формулировке задачи (1), (2), (4), (5). Согласно вариационному принципу Даламбера, их можно записать в виде следующего вариационного уравнения:

  I

  
  

  dz -j a x j

  
  

  )     N

  F 5 udG + ^J п^{( q} ’
  
  ;            i

  
  

  d J ( q ’

  + —— a x i

  
  

  —

  
  

  Y ^{( q} ’ 5n^{( q} ’ dG + и(° n

  ;          n:

  
  

  — р ) 5 u_tdS +

  
  

N

+ EJK J ⁽ q ’ — 1 ⁽ q ’ ) n - 5n ⁽ q ’ dS = o, ^q = 1 П J

где 5 u — виртуальные перемещения балки, 5n ^{( q} ’ — виртуальные приращения концентраций веществ, образующих материал балки;

• -    формулируются следующие предположения:

• 1)    Область решения задачи — цилиндр G = D х [ 0,1 ] , где D — область, занятая поперечным сечением балки. Граница сечения Г = d D = у, ( х ₃ ) ^У₂ ( Х з ) (см. Рис. 1).

• 2)    Ось O х₃ является центральной осью сечения. В этом случае

Ц x₂dx₂dx₃ = 0.

D

• 3)    Поверхность балки представляется как П = П₀ иП, иП₆ , где П_о — торец при х = 0, И, — торец

при  Xj = 1,  П6  — боковая поверхность. Предполагается, что боковая поверхность свободна от механических нагрузок, то есть

^ j ь = °*

Также считается, что массоперенос через боковую поверхность отсутствует:

J q )|   = °*

¹П b

• 4)    Материал балки изотропен:

C k = X5 j 5 _к1 + ц ( 5 к 5 jl +5₈5 ,_к ) ,   a j ) =5 „ а q ,   D j ) =5 D ,   Л j ) =5 „ 5_йЛ q ,           (10)

где X и ц — обезразмеренные коэффициенты Ламе, 51? — символ Кронекера. При этом, в силу (3),

X + 2ц = 1.

• 5)    С точки зрения процесса массопереноса материал балки — идеальный твердый раствор. В этом случае [15-18]

g⁽ qr )=5 ,     D)^q )g⁽ qr' = £>^{( q} ) =5 D .                                        (11)

g           qr , ij g           ij        ij q .

• 6)    Рассматривается изгиб балки в плоскости O х₃х₂ . Тогда и_к = и_к ( х₁ , х ₂,т ) , при этом ( к = 1,2 ) , и₃ = °, Б_й = ° ( i = 1,3 ) . В этой же плоскости осуществляется массоперенос: ц^{1 q} ) = П q ) ( X , х ₂,т ) ■

• 7)    Поперечные прогибы считаются малыми. Сечения, перпендикулярные оси балки до деформации, остаются плоскими и после деформации (гипотеза плоских сечений). Тогда искомые величины и ( х₁ , х ₂, т ) , и₂ ( х , х₂ ,т ) и n^{( q} ) ( х , х ₂,т ) , линеаризованные по переменной х ₂, могут быть представлены в виде [12-14]:

и 1 ( х 1 , х ₂ , т ) = и ( х 1 , т ) + х ₂ х ( х 1 , т ) ,       и ₂ ( х 1 , х ₂ , т ) = v ( х 1 , т ) + х ₂ v ( х 1 , т ) ,

П^{( q} ) ( х , х 2 , т ) = N q ( х , т ) + х 2 H q (х ,т ) .

• 8)    Вследствие принятой гипотезы Бернулли-Эйлера поперечные сечения после деформации остаются нормальными к изогнутой оси балки. Кроме того, при свободной от нагрузок боковой поверхности можно полагать, что деформации вдоль оси O х ₂, ввиду малости, отсутствуют. Тогда [12, 14] (штрих означает производную по переменной х )

  ди ₂

  £ ₂₂ =---

  д х₂

  
  

  = у = ° ^ V = °,

  
  

  х ( ^х 1 , ^т) = ^- v ' ( ^х 1 , ^т) ,

  
  

а равенства (12) запишутся так:

Uj ( х, х2, т) = и (х,, т)-х^'(х,, т), и2 (х,, х2, т) = v (х,, т), П(q) (х1, х2, т) = Nq (х1, т) + х2Hq (х1, т) .

С учетом (10), (11) и (13) компоненты тензора напряжений и вектора диффузионного потока будут иметь вид:

NN

СТ 11 = ( ^и '- ^х 2 v ")^- Е ^а q ( N q ^{+ х} 2 ^Hq ) ,   ^ 22 = ^X( ^и '- ^х 2 v ")^- Е ^а q ( ^Nq ^{+ х} 2 ^Hq ) ,   ^ 12 = °,

.._          (14)

J 1 ^{( q} ) =- D q ( N q + х 2 H q ) + Л q ( и "- х 2 v^m) ,    J 2 ^q ) =- D q H q -Л q V "  ( q = 1, N ) .

В результате подстановки равенств (7)-(14) в (6) получаются уравнения упруго-диффузионных колебаний балки [12]:

• -    продольных

n( и = и "-Уо, N‘+ --  N = DN:-Ля и" + y-;

qq       q   qqq q=1          FF

• -    поперечных

v-av = VV + У a,H"-q+m,  H = ПН+Л, vIV + —-  — = a.(16)

jj          q   qqq j=1           F                                 J 3

В (15), (16) приняты обозначения: F — площадь поперечного сечения балки; J₃ — момент инерции сечения относительно оси O х ₃; распределенные погонные нагрузки, соответственно, продольная n , момент m и поперечная q ; y ^{( q} ) и z ⁽ q ) — линейные плотности объемных источников массопереноса.

Уравнения (15), (16) дополняются краевыми условиями, которые также вытекают из вариационного уравнения (6). В соответствии с постановкой исходной задачи, математическая модель упругодиффузионного изгиба консоли под действием сосредоточенной нагрузки, приложенной к свободному концу, включает в себя уравнения (16) при m = 0, q = 0 и z ^{( q} ) = 0 и следующие граничные условия:

H l „= 0-   ( DH +Л v ")l  = 0-

4 = 0 = °.    v x = 0 = ⁰

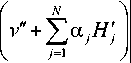
q\x = 0               q Ч 4       ^q    /|x = 1

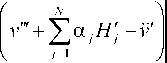
= ^f >2 (^T) .

Начальные условия полагаются нулевыми.

3. Метод решения

Основная проблема заключается в невозможности построения решения поставленной задачи в виде тригонометрических рядов Фурье. Это существенно осложняет обращение преобразований Лапласа, которое также требуется в применяемом подходе. Для преодоления возникающей трудности используется метод эквивалентных граничных условий [17, 18], который заключается в выполнении ряда шагов.

Вначале вместо исходной задачи рассматривается вспомогательная задача (16) с граничными условиями:

v ]   - 0.     v t . 1 = f 2 ( т ) .

x = 0

( D q H q + ^Л q v" )| x = ₀ = У+2.1 ( т ) .    ( D q H q + ^Л , V ')| x = 1 = ^0-

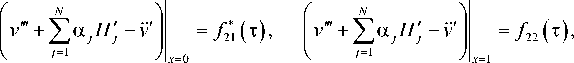
где функции f 2 ( т ) , f ,+₂1(т ) , f ,* ( т ) подлежат определению. С учетом (19) решение приобретает вид [12]:

тт v (x. т) = J^ G12 (x - т-t) fl (t)- G12 (1 - x - т-t) f>2 (t)] dt -j G11 (1 - x - т-t) f 2 (t) dt + 00

N т

+ EJ У p + 2 ( x ^{- т-} t ) У₊ 2-1 ( t ) dt ^-

P = 1 0

тт

Пq (x- т) = J [Gq+1-2 (x- т- t ) f2*1 (t)- Gq+1-2 (1 - x- т- t ) f -2 (t)] dt - J Gq+1-1 (1 - x- т- t ) /12 (t ) dt + 00

N т

+ EJ G q + 1- p + 2 ( x ^{- т-} t ) ^f, 2 + 2.1 ( t ) dt ^-

P = 1 0

где G_mk — поверхностные функции Грина задачи (16), (19), которые являются решениями следующих задач:

..

IVIV

^G ‘ k - a ^G 1 ^k = ^G 1 k ⁺ ^ ^a j^Gj +1, k ,     ^Gj + 1, k = ^Dq^G q₊1, k ^{+ Л} q^G 1 k ;

N

G k + Z « 55 k - G_k j = 1

j=1 (    N)

= 8„8(t), G'\ п=8,,8(т), G* + ?a G ' k -G'=

2k \ ) ~           1 k |^| =0        1 k \   *7        I 1 k               j    j+1,k        1 k I

X j = 0                                                              ^           j = 1                         ^ X j = 1

Gk^ =1 = 0,    ( DqG; +1, k +Л qGk )L 0=5 q+2, k 8(t) ,   (Dq G'q+1, k +Л qGk ^,=

1                                                              X i =0                                                                           I X l =1

Для нахождения функций Грина используется преобразование Лапласа по времени и разложение в тригонометрические ряды Фурье. После применения указанных действий к задаче (21), (22), получается система линейных алгебраических уравнений (индекс L — означает трансформанту Лапласа, Х_и = п n , n = 0,1,2,...):

A (X , , 5 ) GL (X , , 5 )-Xn £ «jGM k (X , , 5 ) = Fk (X , ),    kq+1 (X , , 5 ) G^ k (X , , 5 )-Л q X ' G^c (X , , 5 ) = Fq+1, k (X , ) , j=1

G Lk (») =

⁺ E G mk ( ^X n , ⁵ ) ^{cos X} n^X ,   G mk ( ^X n , ⁵ ) = ² J G mk ( ^X , ⁵ ) ^{cos X} n^X d ^X ,

to

n = 1

^k 1 ( ^X n , 5 ) = ( ^X 2 ⁺ a ) 5 ² + ^X 2

k q + 1 ( X n , 5 ) = 5 + D q X i ,

F 1 k ( X n ) = -2X 2 8 1 k + 28 ₂ k ,     F 1 k (0) =8 ₂ k ,     F q + 1, k ( X n ) = 2X„²Л q 8 1 k - 28 q + 1, k ,     F q + 1, k (0) =-8 q + 1, k .

Решение этой системы находится по формулам Крамера и имеет вид:

G qLC 1,1 ( X n , 5 ) =

g L ( 0, J i = —, a5

GLcK а- P k ^(X n , ⁵ ) ^{G 1} k ^(X n , ⁵ ) = 1^ ’

G + k ( ⁰, 5 ) =-

G q ^L C 1,2 ( X n , 5 ) =

8 q + 2, k

■------------------------------------------------------------------------------------------------ ,

s

P q + 1,2 ( X n , 5 )

2Л q X n

P q + 1,1 ( X n , 5 )

^kq + 1 (^X n , ⁵ )^{+   Q}q (^X n , ⁵ ) ’

G^, p + 2 ( X n , 5 ) =

Q q (^X n , 5 )   ’

'^ qp

^kq + 1 (^X n , ⁵ )

^Pq + 1, p + 2 ^(X n , ⁵ )

Q q (^X n , 5 )   ’

где

N

P (X „, 5 ) = k1 (X „, 5 )n(X „, 5 )-X2X« j ЛjЛj (X „, 5 ),    Qq (X „, 5 ) = kq+1 (X „, 5 ) P (X „, 5 ) , j=1

P 11 ( X n , 5 ) = -2X 2 n ( X „ , 5 ) + X 2 £ a j Л j П j ( X „ , 5 ) ,

^P12 ^(X n , ⁵ ) = ^{2 n(X} n , ⁵ ) ,     ^P1 q + 2 ^(X n , ⁵ ) =  2a q ^X n ^П q ^(X _n , ⁵ ) ,     P q + 1, k ^(X „ , ⁵ ) = ^Л q ^X n^P1 k ^(X n , ⁵ ) ,

NN

n ( X „ , 5 ) = П k q + 1 ( X n , 5 ) ,    П q ( X „ , 5 ) = П k j + 1 ( X n , 5 ) .

j = 1                                                j = 1, j * q

Так как в полученные равенства (23) входят рациональные функции параметра преобразования Лапласа 5 , то их оригиналы находятся с помощью вычетов и таблиц операционного исчисления [19]:

G=k (0, T)   8 T,    Gqc+1, k (0, t) = -8 q+2,kH (T),    Gk (X n, t)= £ A^ (X n) e5 (X" )t , a                                                                    j=1

GF _t(x„ , t ) = 2(Л ^x28_lt-8_ Ae q + 1,Л.       n                     q n             q + ,л.

,- D q X n T

^ 1 ⁽ k ²⁾ ( X n ) =

P 1 k ( X n , 5 j )

N + 3

■ У A?.» ( X n )

I = 1

e^si ^(X n ) ^T

^P '( ^X n , 5 j ) ,

A q + 1, k ( x n ) =

P q + 1, k ( X n , 5 l )

Q q ( x n , 5 i ) .

Здесь:   H ( т)  — функция Хевисайда; s_; ( X_n )    ( j = 1, N + 2 )  — нули многочлена   P ( Х„ , s ) ;

s.;з(\1) = -Dq^2  — дополнительный нуль многочлена  Qq (Х„, s); штрих означает производную по параметру s.

Далее строятся соотношения, связывающие правые части граничных условий обеих задач — исходной и вспомогательной. Так как решение вспомогательной задачи (16), (19) должно удовлетворять граничным условиям исходной задачи для консольно-закрепленной балки (18), то с учетом представлений (20) выражения связи могут быть записаны в виде системы интегральных уравнений Вольтерра 1-го рода [17, 18]:

N + 2 ^т

EJ aij (т-t) y, (t) dt = фДт), j=1 0

где (штрихом обозначается производная по переменной x )

a11 (Т) = G12 (0 Т) ,     a12 (Т) = -G11 С1, Т),     a1,p+2 (Т) = G1,p+2 (0 Т) , a21 (т) = G" (1,т) + £ajGj+1,2 (1,т),    a22 (т) = -G^ (0,т)-£ ajGj +1,1 (0,т), j=1                                                                  j=1

a 2, q + 2 ( т ) = G ,q + 2 ( 1, т ) + Е а ^ + 1, q + 2 ( 1, т ) ,

J = 1

a q + 2,1 ^(т) = ^Gq + 1,2 ^{( 0, т)} ,      a q + 2,2 ^(т) = - ^Gq + 1,1 ^{( 1, т)} ,      a q + 2, p + 2 ^(т) = ^Gq + 1, p + 2 ^{( 0, т)} ,

У 1 ( ^т ) = ^f 21 ( ^т ) ,     У 2 ( ^т ) = Л 2 ( ^т ) , Ур + 2 ( ^т ) = ^fp + 2,1 ( ^т ) ,

Ф 1 ( т ) = J G 12 ( 1, т ^- t ) f 22 ( t ) dt ,    Ф q + 2 ( т ) = J G q + 1,2 ( 1, т ^- t ) f ,2 ( t ) dt ,

о

т

о

Ф2 (T) = J G12 (0 t -T) + Ea JGJ+1,2 (0 Т- t ) f22 ( t ) dt ■ о _

Следует заметить, что ряды Фурье в представлениях для G"_ы , в соответствии с формулами (23), (24), сходятся только в обобщенном смысле, что затрудняет применение для решения системы (25) численных алгоритмов. Для преодоления указанной сложности в (25) выполняется интегрирование по частям. Получается система интегральных уравнений относительно производных д у _у /5т :

N +2 т            5У- (t)

EJAij(т-t) —^rdt=ф(т),   ^O^.-to-EAij(т)yj(0),

J=1 0                  5 t тт-

40) = / aj( t) dt,   Au (т-t )=J ay (5) d ^

При этом функции y - ( 0 ) должны удовлетворять определенным соотношениям. Исходя из условия сопряжения начальных и граничных условий в угловых точках пространственно-временной области рассматриваемых задач, а также с учетом нулевых начальных условий полагается, что y . ( 0 ) = 0 .

Система уравнений (26) решается численно, с помощью квадратурных формул. Для этого область изменения времени т [ 0, T ] разбивается с равномерным шагом h = T^N_ на N_T отрезков, и в точках т„ = mh ( m = 0, N _T) вводятся сеточные функции y^J_m =5 y j ( т m )/5т , A m = A ij ( т _m ) . Каждый из интегралов в (26) при т = т_т заменяется приближенной суммой, соответствующей квадратурной формуле средних прямоугольников:

г           5 УУ, ( t )                                                 m - ¹

J A_l J ( т- 1 ) - j^ dt « hs m - 1/2 + hA ^ y m - 1/2 ,    s m. - 1/2 = E A m - 1 + 1/2 У /- 1/2   ( i , j = 1, n + ² ) ,

0                   ⁵ t                                                              1 = 1

т m-1/2 =т m-12+т m = h I m - D,    т m -1+1/2 =т m -т l -1/2 = h I m - 1 + jl (m = 1,Nt)-

В результате образуется рекуррентная последовательность уравнений ( m >  1 ) :

систем линейных алгебраических

^А У m - 1/2

^Ь m — 1/2 ,

где  Уm—1/2 =(ymm—1/2 )(iV+2)xl  — столбец неизвестных, образом:

а остальные

величины определяются следующим

^A = ^{( A}2 ) ( N + 2 ) x ( N + 2 ) ^{,      Ь} m ^—1/2 = ⁽ b m ^—1/2

) ( N + 2 ) х 1 ’        m — ^{1 1/2}

_ Фi (тm )

—

h

N + 2

E ^ij S m — 1/2 .

J = 1

Ее решение находится по формулам Крамера:

y m — 1/2

А ^J m

~ А

где А = det А , А ^J — определители Крамера для матриц, полученных из матрицы А путем замены J -го столбца столбцом b_{m 1/2} .

Окончательный вид решения исходной задачи находится в результате численного расчета сверток функций Грина вспомогательной задач (21), (22) с функциями, определенными из решения системы уравнений (26). Таким образом, уравнения (20) запишутся так:

т

V ( x , т ) = J

-  /        А f *1 (t)    ~  /            аЛ 2( t)   ~  /            xf * (t)

dt +

G ( x ,т — t )—— — G ( 1 — x ,т — t )---— — G, ,( 1 — x ,т — t )——

¹²               d t        ¹²                   d t        ¹¹                   d t

т

Пq (x, T) = J

^т -N.

+ Jz p + 2 ( x , т— t )          dt ,

0 p = 1                          ^d t

~              x f * (t)   -     ,           Л( 2( t)   -    ,           ^f*( t)

^{G J} q + 1,2 ⁽ x , ^{т —} t ) — ^{G J} q + 1,2 ^{( 1 —} x , ^{т —} t ) —^      ^{G J} q + 1,1 ^{( 1 —} x , ^{т —} t ) ~

dt +

т N

+ Jl ^GG, ..,. 2

₀ p = 1

fp+u (t) dt x, т — t I-----------dt,

v        7    dt

т

<5 mk ( x , ^T ) = J ^Gmk ( x , t ) ^dt .

4. Пример

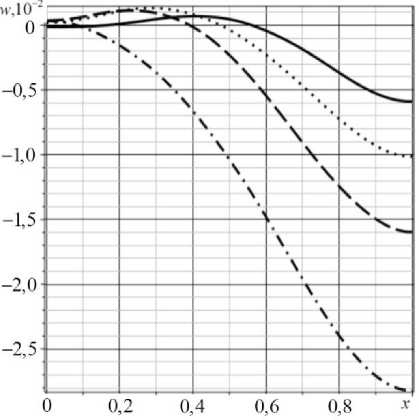
Рис. 2. Прогибы балки v ( x , т ) в разные моменты времени т : 3,3 (сплошная линия); 5 (пунктирная линия); 6,6 (штриховая линия); 10 (штрихпунктирная линия)

Для исследования взаимодействия нестационарных полей (механического и диффузионного) рассмотрена консольно-закрепленная балка длиной l = 1 см с прямоугольным сечением h х b = 0,05 1 х 0,05 1 , изготовленная из 2-компонентного материала, в котором 95% алюминия и 5% меди. В качестве независимого компонента выступает медь [20]. Данные для расчета были следующими (X * , ц * — размерные аналоги упругих постоянных Ламе; верхний индекс 1 указывает на характеристики меди):

X * = 6,93-10¹⁰Н/м², ц * = 2,56 - 10¹⁰Н/м², T = 800 K, р = 2780 кг/м³, 1 = 0,01 м, D * ^{( 1 )} = 6,67 • 10^—14 м²/с, n (1) = 0,05 , а * ^{( 1 )} = 6,14 •Ю ⁷ Дж/кг, m ⁽¹⁾ = 0,064 кг/моль.

Поперечная нагрузка, приложенная к свободному ( x = 1) концу балки, задавалась в виде:

f 22 (т)= H (т).

Численное решение системы (26) и подстановка найденных функций в свертки (28), дает в результате прогибы балки, приведенные на рисунке 2.

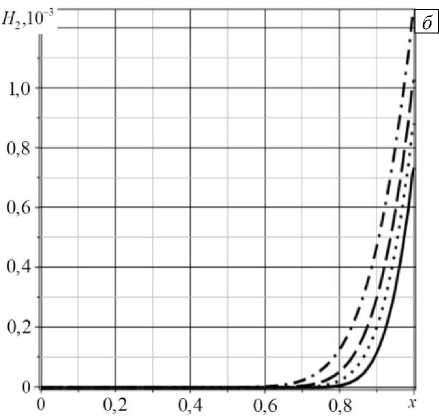
На рисунке 3 показано, как изменяются распределения концентраций меди (Рис. 3 а ) и алюминия (Рис. 3 б ) в результате нестационарного изгиба консольно-закрепленной балки.

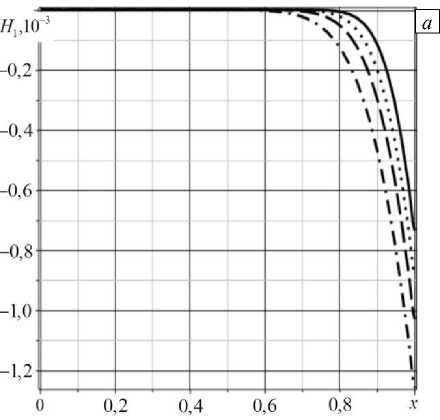
Рис. 3. Линейная плотность приращения концентрации меди ( а ) и алюминия ( б ) в разные моменты времени т : 3,3 - 10¹² (сплошная линия); 5 - 10¹² (пунктирная линия); 6,6 - 10¹² (штриховая линия); 10¹³ (штрихпунктирная линия)