Нестационарный износ двухслойного покрытия с учётом тепловыделения от трения

Одним из путей повышения работоспособности высоконагруженных узлов трения являются разного рода защитные меры, в частности, нанесение двухслойных покрытий, в которых верхний слой обеспечивает антифрикционные свойства, а нижний — несущую способность и демпфирование [1]. Эффективность такой композиции существенно зависит от применяемых материалов, а также от конструкции и соотношения геометрических размеров основных элементов. В настоящее время тонкие двухслойные и многослойные покрытия, в том числе керамические — нитридные [2, 3], оксидные [3], оксинитридные [3], карбидные [5], карбонитридные [6] и другие [7, 8], — предохраняют поверхности трения от разрушения в самых различных областях техники. Такое широкое использование связано с их высокой износостойкостью, которая обуславливается твердостью при высоких температурах, химической

инертностью, жаро- и коррозионной стойкостью. Тонкие керамические покрытия наносятся также на режущий, штамповый инструмент. Нитридные покрытия, являющиеся полупроводниковыми материалами, имеют хорошую перспективу для приложения в современных электронных устройствах.

При отработке технологии создания износостойкого покрытия необходимо, исходя из его термомеханических характеристик, осуществить прогноз эксплуатационных свойств, которые приобретёт защищаемая поверхность. Каждое использование покрытий требует тщательного анализа и баланса предъявляемых, зачастую противоречивых, требований к их эксплуатационным качествам. Наиболее эффективным средством определения оптимальных параметров является математическое моделирование, которое позволяет учесть практически любое количество защитных слоёв, осуществить подбор их физикомеханических, геометрических и других параметров, наилучших с точки зрения износостойкости, минимизации разогрева от трения, недопущения нештатных ситуаций при эксплуатации, таких как термоупругая неустойчивость и резонансные явления. В последнее время появляется все больше работ, посвященных исследованию функционирования покрытий [9–25], в том числе двухслойных [9–15], при наличии тепловыделения от трения без износа [19–22] и с его учётом [23–25]. Однако теоретического исследования в двухслойной композиции свойств компонентов на износ в условиях фрикционного тепловыделения ранее не проводилось, в то время как с величиной температуры на скользящем контакте напрямую связана степень износостойкости деталей машин и инструмента [26].

В настоящей статье оценивается состояние двухслойного покрытия, подвергающегося изнашиванию от взаимодействия с жёстким штампом. Принимаются предположения недеформируемости штампа и его незначительного по сравнению с покрытием износа, что моделирует лабораторные условия проведения испытаний [27]. Процесс изнашивания покрытия сопровождается разогревом от трения. В силу того, что жёсткость нижнего слоя существенно ниже жёсткости подложки, последняя представляется как недеформируемая полуплоскость. Решение соответствующей нестационарной начально-краевой задачи с помощью интегрального преобразования Лапласа по времени сводится к решению системы обыкновенных дифференциальных уравнений в трансформантах [22, 24, 25, 28, 29]. Обращение полученных трансформант осуществляется методами теории функций комплексного переменного по аналогии с работами [22, 25, 28]. Полученное решение контактной задачи позволяет подбирать параметры слоёв покрытия как для повышения его износостойкости, так и минимизации разогрева от трения.

2.    Постановка задачи

Рассматривается задача изнашивания двухслойного покрытия жёстким штампом при скользящем термофрикционном контакте. Штамп в виде жёсткой полуплоскости I с постоянной скоростью V движется по поверхности двухслойного термоупругого покрытия. Верхний слой — А , сцеплен по нижней грани со слоем B , который по своей нижней грани соединён с недеформируемой подложкой II (Рис. 1).

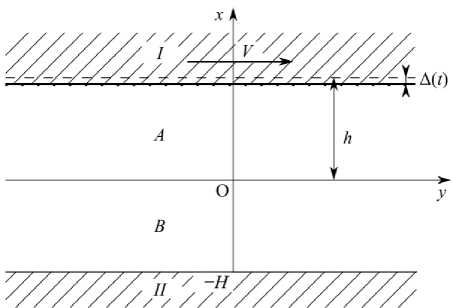
Рис. 1. Схема к постановке задачи

Одновременно с поступательным движением полуплоскость I внедряется в упругое покрытие по нормали к его поверхности. Скольжение            теплоизолированной недеформируемой     полуплоскости     I по поверхности контакта вызывает износ и кулоновское трение, порождающее тепло. Тепловой поток, образующийся за счёт трения на контакте, направлен вглубь двухслойного покрытия. В начальный момент времени смещения и температура в слоях покрытия равны нулю.

Согласно     формулировке     задачи деформирования двухслойного покрытия, все основные физические характеристики упругих слоёв — температура, напряжения, смещения — не зависят от горизонтальной координаты и являются функциями только вертикальной координаты x и времени t . Таким образом, деформирование термоупругого покрытия можно описать системой дифференциальных уравнений плоской задачи теории упругости совместно с уравнением теплопроводности:

1,2                ∂σ1,2

^{∂σ xx} = 0 ,           ^xy = 0 ,

∂x            ∂x

92Tl_JLдT2 - о дx2    к12  д t      ’ t > 0.

Здесь: о^(x, t), о (x, t) — нормальные и касательные напряжения; T(x, t) — температура; к — коэффициент температуропроводности; индексами 1 и 2 обозначены характеристики верхнего A (0 < x < h) и нижнего B (-H < x < 0) слоёв покрытия соответственно.

Связь между напряжениями, смещениями и температурой устанавливают формулы Дюамеля-Неймана [30]:

с

1,2

xx

² 0 1,2 ⁽¹ -V 1.2 ) ^д u 1,2    2 0 1,2 ^{(1 + V} 1,2 )    „

—^,-------^,--^,---^,------- 1— а , ₂ Т

1 - 2v₁₂     д x       1 - 2v₁₂      ’   ¹

1,2         ^{д W} 1,2

о = О,       , xy     1,2  дx

где u ( x , t ) , w ( x , t ) — вертикальные и горизонтальные смещения, ц — модуль сдвига, v — коэффициент Пуассона, а — коэффициент линейного расширения материалов верхнего и нижнего слоёв покрытия. Подставляя (3) в (1), получим уравнения термоупругости в смещениях:

^д u 1,2 _ 1+У1,2      ^{д T} ,2

д x ²    1 - v₁₂  ^1,2   д x ’

д ² W ₂

---= 0

д x ^{2       ,}

t >  0.

Граничные условия для уравнений теплопроводности (2) и термоупругости (4) запишем в следующем виде: - механические

x = h : U1 (h, t) =-А( t) + u w( t), (5) Oxy (h, t) = -f Oxx (h, t) , (6) x = 0: u1 (0, t) = u2 (0, t) ,       cxx (0, t) = cxx (0, t) , (7) W1(0, t) = W2(0, t) ,      °x, (0, t) ^xy (0, t) , (8) x = - H : u2 (-H, t) = 0 , (9) w2 (- H, t) = 0; (10) - температурные x = h : K^Ti^h^ =-Q(t), дx (11) x = 0: T1(0,t) = T2(0,t),    K1        = K2 8TM, дx          дx (12) x = - H : T2(-H, t) = 0, (13) где uw (t) — износ покрытия, Q(t) = -fVо^Дh, t) — количество тепла, образующегося на контакте вследствие трения [19], f— коэффициент трения, А(t) — закон внедрения полуплоскости I в упругое покрытие, K, К2, h, H — коэффициенты теплопроводности и толщины верхнего и нижнего слоёв покрытия соответственно. Для описания износа воспользуемся линейным законом:

t u w( t) = - fVK * J°L(h, t) d T ,

где K* — коэффициент пропорциональности между работой сил трения и количеством удалённого с поверхности контакта материала.

К дифференциальным уравнениям (2), (4) необходимо добавить нулевые начальные условия на смещения uv, w2, u2, w2, температуру T, T2 и закон внедрения А(t):

U ( x ,0) = u ₂( x ,0) = w ( x ,0) = w₂ ( x ,0) = 0,     T ( x ,0) = T ( x ,0) = 0, А (0) = 0 .

Следует заметить, что вертикальные смещения u_{x 2} ( x , t ), нормальные напряжения a²² ( x , t ) и температура T ₂ ( x , t ) в слоях покрытия не зависят от горизонтальных смещений w ₂ ( x , t ). Горизонтальные смещения определяются из второго уравнения в (4), второго уравнения в (3), граничных (6), (8), (10) и начальных условий (15) через нормальные напряжения а*_х ( h , t ).

3.    Метод решения. Основные формулы решения

Решение квазистатической начально-краевой задачи (1)-(15) строится с помощью интегрального преобразования Лапласа [31]. В результате получается система обыкновенных линейных дифференциальных уравнений относительно неизвестных трансформант u L^ ( x , z ), T L ( x , z ), w L₂ ( x , z ). После их нахождения и обращения по Лапласу искомые решения поставленной задачи записываются в виде свёрток Лапласа:

в которых

t z X 1 — V]   V Г . , x p I t — т | 7

T ( x , t ) =;-- 7 I ^А ( т ) f I x ,----- I d т ,

• ^{1 + V а} 1 ^{h J}0          (    t k J

, _x    X M . + xh -¹

• u , ( x , t ) =--

• 1          XM. +1

t

^u 1

t -т 1 x ,------ I d т , .    t к   J

• 1      .       2ц,(1 -v, ) |   A ( t )      r.,       | t -т |    ]

a* ( x , t ) = -  -------— ------- + А ( т ) f  x ,---- d т ,

( 1 - 2 v * ) h (X M * + 1  ^J_o              t _K J J

t m          1 - Vl  V Г . Z . У I t - т I ,

T 2 ( x , t ) = -—¹— 7 А ( т ) / I x ,----I d т ,

• ^{1    +} V ^a i ^h 0         I    t k J

,   ,    M. ( X + xh ^- * )

u 2 ⁽ x ’ t ) =--

XM. + 1

t

^u 2

- H <  x <  0 ,

t -т 1 x ,------ I d т , .    t к   J

• ₂    .   .       2 ц (1 -v, ) |   A ( t )                  I t -т|, ]

a2 (x, t) = -  --------— --------+ А(т) f   x,---- dт , xx          (1 - 2v*) h (XM* +1 J       a2 ( tк J J

t

I                                   I u w( t) = Vkwf А(т) fI —| d т,

0            ( t k J

/ ( x , t ) = —J f a ⁽ x ’ z ) e z dz ,       a = T ₂, u ₂,a,₂,       / ( x , t )

^a            2n i^J_r  t_KR ( z )                           ^{1,2   1,2    1,2         7wV} ’

- H <  x <  0 ,

- H <  x <  0 ,

* J^ z ) e z dz , 2 n i J t к R ( z )

• (16)

• (17)

• (18)

• (19)

• (20)

• (21)

• (22)

• (23)

где Г = { Z ^: - i ” + dt_x , i ” + dt_x } — контур интегрирования, в котором значение d подбирается таким образом, чтобы все изолированные особые точки подынтегральных функций в (16)-(22) лежали левее Г . Подынтегральные функции в (23) задаются формулами

R ( z ) = ( X M * + 1) zr ( h , z ) - V (1 - k _w ) r ( h , z ) +1 —-

,

r ( x , z ) = ch Afzxh ¹ ch JkTx V z + K к.¹² sh Jzxh ¹ sh JkTx V z , N ( x , z ) = V z ( sh 4zxh ch Jk?X V z + K к - ^1/2 ch V zxh sh Jk?X V z ) ,

^X+ xh

N (x, z) = N0 (x, z)--R (z), u1            u1           X M. +1

N a, ( x , z ) = N a, ( x , z ) - ( X M * + 1) ^{- 1} R ( z ) ,

₍ a       ₍ a  M- ( X + xh *) nz X

N (x, z) = N01 (x, z)--- R (z), u2           u2           X M. +1

N ( x , z ) = N 0 ( x , z ) - ( X M * + 1) ^{- 1} R ( z ),

x               I           I   K-      I                   K

N 0 ( x , z ) = I X M. +— I zr ( h , z ) - V I r ( x , z ) + l-- 1 I ch VkX V z--

¹          (         h J              (          (к * L *      J                 к * L *

N0 (x, z) = Vz (sh JKT4zxh 1 ch JK*XVz + ch JK*4zxh 1 sh JK*XVz), xK   x     x

N 0 ( x , z ) = M. I X + — I zr ( h , z )-- V I ch jKTV z — ch VKTXV z + sh VK”V z — sh JKTXV z - 1

²             V     h )           k. L, (            h                         h

N ⁰ ( x , z ) = N ° ( x , z ) = ^zr ( h , z ) ,      N _w ⁽ z ) = r ⁽ h , z ),

t t = —

t K

^х= H ^, h

M. = M , L = L M 2         L 2

h       - ₌ fV « 1 2 ^ 1 (1 + V 1 ) h

K1 ’             K1      1 - 2 v1’

K1

Kt         ,      ^K*         ,     "^^1 2

K2             k2

_{k =} (1 -v , ) K 1 K *

^{w (1} + ^V 1 ) « 1 ^K 1 ’

² 0 1,2 ^{(1    V} 1,2 )

1 - 2 V 1,2

• ,2

1 +2 12.

^{1 -V} 1,2

« 1,2

Таким образом, решение поставленной в разделе 2 задачи свелось к вычислению в (16)-(22) следующих квадратур: T_{x 2}( x , t ), u_{x 2}( x , t ), □!? ( x , t ), u _w ( t ). Использование методов теории функций комплексной переменной для вычисления квадратур позволяет представить решение рассматриваемой задачи в виде сумм по полюсам подынтегральных функций, являющихся нулями функции R ( z ) из (24).

Горизонтальные смещения w, 2(x, t) определяются интегрированием второго уравнения в (4) и с учётом условий (6), (8), (10) выражаются через контактные напряжения а^Сh, t) как w1(x, t) = - f |V(x + HM ^Ox, (h, t ) ,      w2 (x, t ) = - f |V(x + H )axx (h, t) .              (27)

Отметим, что при H = 0 формулы (16)-(18), (22), (27) сводятся к выражениям, полученным ранее другими авторами для случая изнашивания однослойного покрытия (см. [24]), но при условии, что в [24] Bi ^ го , где Bi — число Био.

• 4.    Особые точки подынтегральных функций в комплексной плоскости

Полюсы подынтегральных функций в (16)-(22) совпадают с нулями R ( z ) из (24), за исключением тех нулей R ( z ), которые являются устранимыми особыми точками подынтегральных функций. Для отыскания нулей R ( z ) в комплексной плоскости z = с + i п решается уравнение:

- 1 1 ch JKx V z - —1 = о.

)                   k . L . I

R ( z ) = ( X M . +1) zr ( h , z ) - V (1 - k„ ) r ( h , z ) + —-I Ik . L .

Как видим, нули R ( z ) зависят от r ( x , z ) (см. (25)) и семи безразмерных параметров задачи: V , k_w , X , M, , K, , к., L, , определяемых по формулам (26). При исследовании поведения нулей R ( z ) из (28) при фиксированных значениях k_w , X , M, , K, , к., L, и переменном параметре V , который изменяется от 0 до го , использовался опыт авторов работ [23, 24].

• 5.    Эффективные формулы решения задачи

С учётом поведения подынтегральных функций (23) на бесконечности, их мероморфности в комплексной плоскости и в предположении, что все полюсы Zk ( k = 0,1,2,...) подынтегральных функций в (23) однократные, с помощью методов теории функций комплексного переменного [32] имеем

N ( x.z )

^fa ⁽ x , t ) = Е ^B a ⁽ x ’ ^Z k ^)eX P ^{( Z} k t ) ,      ^B a ⁽ x , z ) = . V-z . ,                              ⁽²⁹⁾

k =0                                           t к ^{R (} z )

где полюсы Zk даются общим списком, упорядоченным по модулю: |Z₀|^|Zi|- ■■■ — |С*| — ■■■ .

Подставляя формулы (29) в (16)-(22), получим новые выражения для решения задачи — в виде рядов по полюсам:

1 _ v   JZ  го

T 1 ( x , t ) = ----¹ — ^ Bt ( x , Z k ) D ( Z k , t ),

0 — x — h ,

1 + V 1 « 1 h k =0    ¹

U1( x, t) = -XM* + xh А( t)-Z B^ (x, Z k ) D(Z k, t) ,     0 - x - h ,(31)

X M. +1       ^0

X2(x, t) = Ь^- V- £ B (x, zk)D(Zk, t),     -H - x - 0 ,(32)

1 + v 1 a , h k = o ²

u2(x,t) = -M' X/ xh 1) А(t)-£B (x,Zk)D(Zk,t),     — H - x - 0 ,(33)

X m. +1

U w( t) = Vw Z Bw(Z k) D (Zk, t),     Bw( -) = -w^,(34)

k = 0                                        t к R ^{( -} )

| t-T | в которых D(-, t) = А(т)ехр -

0            V t к 7

Отметим, что напряжения в рассматриваемой задаче не зависят от вертикальной координаты x , поэтому

^xx2(x,t) = CTxx(t),      -H - - - h, и формула для их вычисления принимает вид:

ст xx ⁽ t ) =

2 ^ 1 (1 -V 1 ) [   A ( t )

(1 - 2vj) h (x M. + 1

да

+ Z B „ ( Z k ) d ( Z k , t ) k = 0

B _T ( - ) =

- _T ( h , - ) t к R '( - )

- H - x - h .     (35)

Формулы (30)–(35) позволяют проанализировать устойчивость решения задачи [22, 24, 25, 33].

В предположении, что функция А ( t ) является ограниченной на t е (0, да ), и при условии существования хотя бы одного полюса Zk ( k = 0,1,2,...) с Re(Z_t) >  0 справедливо:

|да при Im(Zk ) = 0, при Im(Zk) * 0,

lim D (Zk, t) =^ t >да            Iне существует и полученные решения неустойчивы. С механической точки зрения в этом случае наступает термоупругая неустойчивость скользящего контакта [22, 24]. Характер поведения решений задачи термоупругого износа однослойного покрытия при термоупругой неустойчивости рассматривался ранее в [28].

6.    Численные результаты

Численный анализ полученных решений рассматриваемой задачи осуществлялся с помощью формул: (30) — для температуры T ( x , t ), (34) — для износа u _w ( t ), (35) — для напряжений а^ ( t ). Максимальный уровень проседания жёсткой полуплоскости I в упругое покрытие задавался параметром А_о, а закон её внедрения А ( t ), состоящий из активной фазы на временном интервале 0 <  t <  t_E и пассивной фазы на интервале t _E<  t < да , описывался формулой:

А ( t ) = А ₀ ( t _Е ^{- 1} tH ( t _Е- 1 ) + H ( t - 1 _E ) ) ,       t >  0 ,

где t_E — время окончания активного участка внедрения, H ( t ) — функция Хевисайда. Процесс изнашивания покрытия на величину А_о считался завершенным в момент времени t_w , когда u _w ( t _w) = А_о.

Распространённым на практике материалом для износостойкой защиты является нитрид титана (TiN). Современные методы нанесения позволяют создавать под слоем из него слой металлического титана различной толщины [2]. Влияние соотношения толщин верхнего и нижнего слоёв покрытия на характеристики его изнашивания можно видеть на рисунке 2, где даны графики изменения во времени основных характеристик скользящего контакта: напряжений p(t) = -стхг (t) , температуры на контакте с деформирующим элементом T(t) = T (h, t), износа uw (t). Термомеханические параметры материала верхнего слоя A соответствуют нитриду титана: п, =100,4 ГПа, у, = 0,25 , к, = 6,11 -10-6 м2/с, а, = 9,35-10—6 1/К, К =19,2 Вт/(м-К), f=0,84, К*=1,94-10-5 мм3/(Н-м) (значения параметров f и К* взяты из работы [27]); параметры материала нижнего слоя B отвечают титану: ц2 = 44,0 ГПа, v2 = 0,32 , к2 = 8,99-10-6 м2/с, а2 = 8,60-10—6 1/К, К2= 21,9 Вт/(м-К); другие характеристики следующие: скорость скольжения V = 5,0 мм/с, параметры закона внедрения t =10 с, Δ=0,2 мкм, общая толщина покрытия h + H = 20 мкм. На рисунке 2 номера кривых соответствуют различным значениям параметра X, задающего отношение толщин нижнего и верхнего слоёв покрытия:

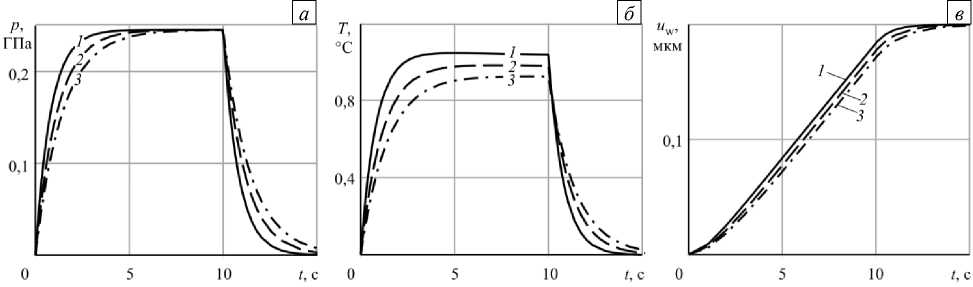
Рис. 2. Основные характеристики скользящего контакта при изнашивании двухслойного покрытия для различных значений параметра X : 0,00 (кривая 1), 0,33 (2), 19,00 (3); контактные давления  p(t) (а), температура на контакте Т(t) (б), износ покрытия uw (t) (в)

В таблице для различных значений толщин верхнего ( h ) и нижнего ( H ) слоёв покрытия приведены значения относительной толщины нижнего слоя X , времени износа покрытия t_w и наибольшей температуры на контакте Т_х * = max Т ( h , t ), t е (0, t _w ]. Рисунок 2 и таблица показывают, что с увеличением толщины нижнего слоя покрытия увеличивается время износа (то есть замедляется изнашивание покрытия) и падает относительная контактная температура Т_х * / Т_о * (то есть уменьшается разогрев от трения на контакте).

Таблица. Значения основных характеристик процесса изнашивания двухслойного покрытия при различных значениях толщин верхнего и нижнего слоёв покрытия

h , мкм	H , мкм	X	t w , с	T x* / Т
20	0	0,00	11,7	1,00
15	5	0,33	12,3	0,97
10	10	1,00	12,8	0,94
5	15	3,00	13,4	0,91
1	19	19,00	13,9	0,88

7.    Заключение

В результате теоретического исследования износостойкости двухслойного покрытия с учётом его разогрева вследствие трения, создаваемого скользящим по его поверхности жёстким штампом, установлена связь параметров процесса с толщиной нижнего слоя. Она влияет:

• -    на износостойкость двухслойного покрытия в целом;

• -    на температуру разогрева контакта слоёв.

Полученное решение контактной задачи может быть использовано для подбора толщины наносимых слоёв с целью улучшения износостойкости и уменьшения разогрева от трения в высоконагруженных узлах.

Работа выполнена при финансовой поддержке РФФИ (проект № 18-57-00015-Бел_а) и БелРФФИ

(проект № Ф18Р-239).