Несуществование решения затухающей системы нелинейных волновых уравнений типа Кирхгофа

Несуществование решения затухающей системы нелинейных волновых уравнений типа Кирхгофа

Автор: Зеннир К., Зитуни С.

Журнал: Владикавказский математический журнал @vmj-ru

Статья в выпуске: 4 т.17, 2015 года.

Бесплатный доступ

Изучается влияние сильного источника на существование решений в пространстве с высоким порядком суммируемости в затухающей системе нелинейных волновых уравнений типа Кирхгофа.

Короткий адрес: https://sciup.org/14318519

IDR: 14318519

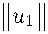
Список литературы Несуществование решения затухающей системы нелинейных волновых уравнений типа Кирхгофа

  • Abdelli M. and Benaissa A. Energy decay of solutions of degenerate Kirchhoff equation with a weak nonlinear dissipation//Nonlinear Analysis.-2008.-Vol. 69.-P. 1999-2008.
  • Agre K. and Rammaha M. A. Systems of nonlinear wave equations with damping and source terms//Diff. Inte. Equ.-2007.-Vol. 19.-P. 1235-1270.
  • Benaissa A., Ouchenane D. and Zennir Kh. Blow up of positive initial-energy solutions to systems of nonlinear wave equations with degenerate damping and source terms//Nonlinear Studies.-2012.-Vol. 19, № 4.-P. 523-535.
  • Benaissa A. and Messaoudi S. A. Blow up of solutions of a nonlinear wave equation//J. Appl. Math.-2002.-Vol. 2(2).-P. 105-108.
  • Benaissa A., Messaoudi S. A. Blow up of solutions for Kirchhoff equation of $q$-Laplacien type with nonlinear dissipation//Colloq. Math.-2002.-94(1).-P. 103-109.
  • Benaissa A., Messaoudi S. A. Blow up of solutions of a quasilinear wave equation with nonlinear dissipation//J. Part. Diff. Eq.-2002.-Vol. 15(3).-P. 61-67.
  • Erhan Piskin and Necat Polat Uniform decay and blow up of solutions for a system of nonlinear higher-order Kirchhoff-type equations with damping and source//Cont. Anal. Appl. Math.-2013.-Vol. 1, № 2.-P. 181-199.
  • Georgiev V. and Todorova G. Existence of a solution of the wave equation with nonlinear damping and source term//J. Diff. Eq.-1994.-Vol. 109.-P. 295-308.
  • Hrusa W. J. and Renardy M. A model equation for viscoelasticity with a strongly singular kernel//SIAM. J. Math. Anal.-1988.-Vol. 19, № 2.
  • Kafini M., Messaoudi S. A blow-up result in a Cauchy viscoelastic problem//Appl. Math. Letters.-2008.-Vol. 21.-P. 549-553.
  • Kirchhoff G. Vorlesungen uber Mechanik. 3rd ed.-Leipzig: Teubner, 1983.
  • Levine H. A. and Serrin J. Global nonexistence theorems for quasilinear evolution equations with dissipation//Archive for Rational Mechanics and Analysis.-1997.-Vol. 37, № 4.-P. 341-361.
  • Levine H. A., Park S. R., and Serrin J. Global existence and global nonexistence of solutions of the Cauchy problem for a nonlinearly damped wave equation//JMAA.-1998.-Vol. 228, № 1.-P. 181-205.
  • Gao Q., Li F., and Wang Y. Blow up of the solution for higher order Kirchhoff type equations with nonlinear dissipation//Cent. Eur. J. Math.-2011.-Vol. 9(3).-P. 686-698.
  • Messaoudi S. Blow up and global existence in a nonlinear viscoelastic wave equation//Maths Nachr.-2003.-Vol. 260.-P. 58-66.
  • Messaoudi S. A. On the control of solutions of a viscoelastic equation//Journal of the Franklin Institute.-2007.-Vol. 344.-P. 765-776.
  • Messaoudi S. A. and Said-Houari B. Global non-existence of solutions of a class of wave equations with non-linear damping and source terms//Math. Meth. Appl. Sci.-2004.-Vol. 27.-P. 1687-1696.
  • Messaoudi S. A. and Said-Houari B. A blow-up result for a higher-order non-linear Kirchhoff -type hyperbolic equation//Appl. Math. Letters.-2007.-Vol. 20.-P. 866-871.
  • Messaoudi S. A. and Said-Houari B. Global nonexistence of positive initial-energy solutions of a system of nonlinear viscoelastic wave equations with damping and source terms//J. Math. Anal. Appl.-2010.-Vol. 365.-P. 277-287.
  • Ouchenane D., Zennir Kh., and Bayoud M. Global nonexistence of solutions of a system of nonlinear viscoelastic wave equations with degenerate damping and source terms//Ukrainian Math. J.-2013.-Vol. 65, № 7.
  • Pohozaev S. I. On a class of quasiunear hyperbolic equations//Mat. Sbornik.-1975.-Vol. 96(138), № 1.
  • Rammaha M. A. and Sawanya Sakuntasathien. Global existence and blow up of solutions to systems of nonlinear wave equations with degenerate damping and source terms//Nonlinear Analysis.-2010.-Vol. 72.-P. 2658-2683.
  • Rammaha M. A. and Sawanya Sakuntasathien. Critically and degenerately damped systems of nonlinear wave equations with source terms//Appl. Anal.-2010.-Vol. 72.-P. 1201-1227.
  • Reed M. Abstract Non Linear Wave Equations//Lect. Notes in Math.-Berlin: Springer-Verlag, 1976.
  • Said-Houari B. Global nonexistence of positive initial-energy solutions of a system of nonlinear wave equations with damping and source terms//Dif. Int. Equ.-2010.-Vol. 23, № 1-2.-P. 79-92.
  • Todorova G. Cauchy problem for a nonlinear wave equation with nonlinear damping and source terms//Comptes Rendus de l'academie des Sciences.-1998.-Ser. 1, Vol. 326, № 2.-P. 191-196.
  • Todorova G. Stable and unstable sets for the Cauchy problem for a nonlinear wave equation with nonlinear damping and source terms//JMAA.-1999.-Vol. 239, № 2.-P. 213-226.
  • Vitillaro E. Global nonexistence theorems for a class of evolution equations with dissipative//Archive for Rational Mechanics and Analysis.-1999.-Vol. 149, № 2.-P. 155-182.
  • Yang Z. Blow up of solutions for a class of nonlinear evolution equations with nonlinear damping and source term//Math. Meth. Ap. Sc.-2002.-Vol. 25, № 10.-P. 825-833.
  • Zennir Kh. Growth of solutions with positive initial energy to system of degeneratly damped wave equations with memory//Lobachevskii J. of Math.-2014.-Vol. 35, № 2.-P. 147-156.
Еще
Статья научная
QR-код для установки приложения SciUp Наведите камеру и скачайте бесплатное приложение SciUp