Нетрадиционные способы составления таблицы очередности игр для проведения соревнований по круговой системе

Спортивные состязания являются неотъемлемой частью жизни профессиональных спортсменов. Наиболее популярны командные игровые виды спорта. Они осуществляются по различным системам проведения соревнований (турниров), в основном по круговой или по олимпийской системе. Существует и смешанная система, когда на разных этапах соревнования проводятся по разным системам.

Олимпийская система (на выбывание) применяется при большом числе участников и ограниченном сроке проведения соревнований [1]. Для ее проведения, согласно поданным заявкам для участия в соревнованиях (турнире), составляется турнирная сетка игр. После жеребьевки команды включаются в сетку в соответствии с полученными номерами. Команда-победитель продолжает борьбу в сле- 68 дующей стадии соревнований (турнира), а проигравшая команда покидает соревнования (турнир).

Для проведения соревнований по круговой системе применяется таблица Бер-гера1. Таблица названа в честь австрийского шахматиста, шахматного теоретика и шахматного композитора Иоганна Непомука Бергера 2.

Таблица Бергера – это таблица очередности игр. Предварительно команды, участвующие в соревнованиях, получают стартовый номер (номер по жеребьевке) и затем по соответствующей таблице определяются пары соперников на каждый тур. Команды, номер которых указан в таблице первым, являются хозяевами поля, или «условными» хозяевами. В интеллектуальных видах спорта (шахматы, шашки) такие команды играют партию белыми. В случае участия в соревнованиях нечетного чис- ла команд в каждом туре одна команда свободна от игры [1].

В случае отсутствия таблицы Бергера возможно использовать другие способы составления таблицы очередности игр3.

Один из способов составления таблицы очередности игр принадлежит К. Брехову. Необходимо начертить круг с отметками в виде черточек, равными количеству участников соревнований (для нечетного числа участников) или округленных до ближайшего нижнего нечетного числа (для четного числа участников) (рис. 1).

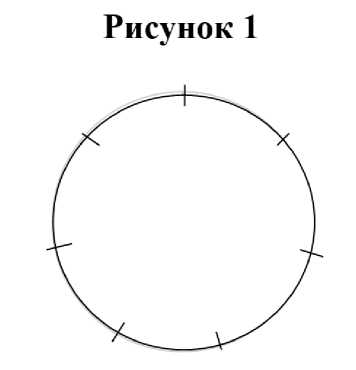
Затем отметки нумеруются по направлению часовой стрелки в возрастающем порядке, начиная с номера «1» (рис. 2).

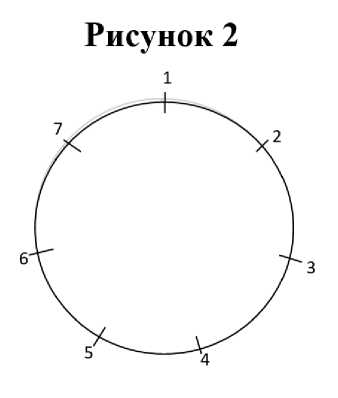
Параллельными линиями соединяются номера: первый порядковый номер с номером «2»; номер «3» с последним порядковым номером; номер «4» с предпоследним порядковым номером и т. д. (рис. 3).

Рисунок 3

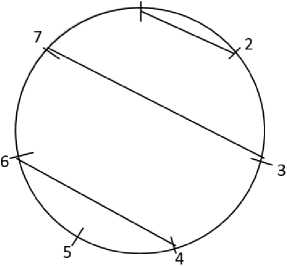
Способ, предложенный К. Бреховым, приводит к нестандартным парам таблицы очередности игр для проведения соревнований по круговой системе.

Для приведения способа К. Брехова к стандартной таблице Бергера необходима ее модернизация: после двух первых действий, предложенных К. Бреховым (рис. 2), количество участников условно делится на две части. В случае нечетного количества участников происходит округление до ближайшего верхнего четного числа, чередованием их из верхней и нижней части, начиная с наименьшего номера. Полученные сведения заносятся в таблицу, где в первый столбец сверху вниз в порядке возрастания заносятся номера туров, начиная с первого, во второй – номера участников (таб. 1).

Данная связка пар номеров является распределением пар участников в пер- 69 вом туре. Номер, оставшийся без пары, остается свободным в данном туре (при нечетном числе участников) или играет с последним порядковым номером равным количеству участников в турнире (при четном числе участников).

В следующем туре первый порядковый номер соединяется параллельной линией с третьим номером, номер «4» – с последним порядковым номером, и так далее до соединения всех номеров параллельными линиями [2].

Общая схема распределения пар участников по турам представлена на рисунке 4.

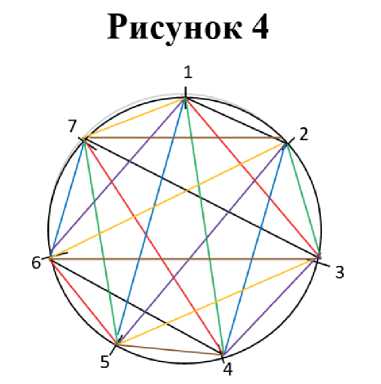
Таблица 1

№ тура	Номер игрока для последнего номера или свободный игрок в туре
1	1 (первый порядковый номер из верхней части)
2	5 (первый порядковый номер из нижней части)
3	2 (второй порядковый номер из верхней части)
4	6 (второй порядковый номер из нижней части)
5	3 (третий порядковый номер из верхней части)
6	7 (третий порядковый номер из нижней части)
7	4 (четвертый порядковый номер из верхней части)

Определяем номер соперника для последнего номера участника (для четного числа участников) или номер свободного участника (для нечетного числа участников) в туре, соответствующему первому столбцу.

После чего с внешней стороны круга рядом с отметкой номером участника ставятся условные фигуры, например, прямоугольной формы с последним номером участника (для четного числа участников) или с номером «0» (для нечетного числа участников) с указанием в скобках номера тура согласно таблице 1.

Условная фигура в данном случае прямоугольной формы соединяется линией с рядом, стоящим номером участника (рис. 5)1.

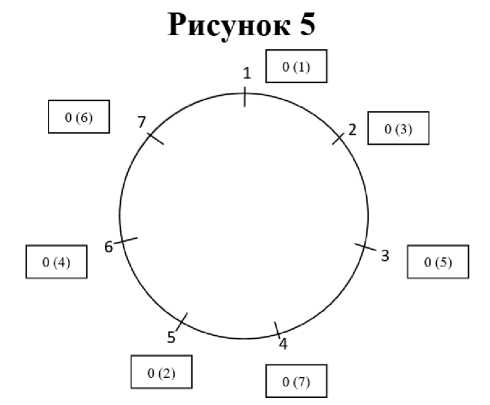
Соседние номера, номера участника, соединенного с условной фигурой, соединяются параллельными линиями. Параллельными линиями соединяются и последующие номера. Так определяются пары участников для данного тура (рис. 6).

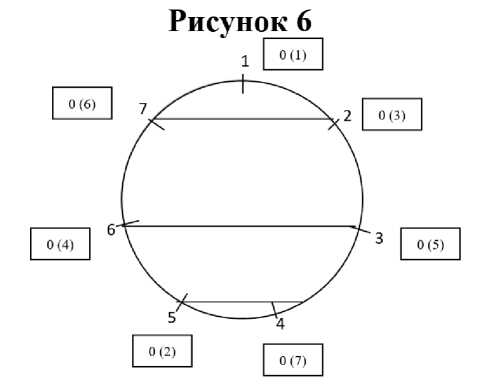
Аналогичным образом происходит распределение пар участников для последующих туров (рис. 7). Модернизированная общая схема распределения пар участников по турам представлена на

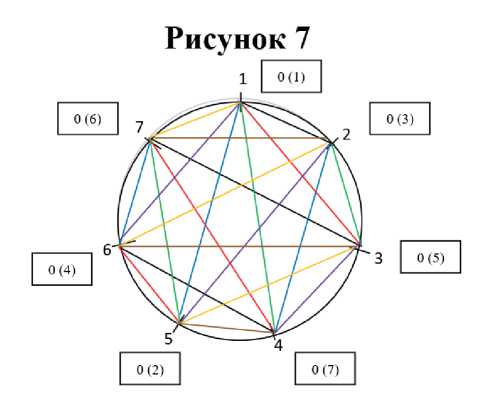
Для определения хозяев поля, или «условных» хозяев (в интеллектуальных видах спорта (шахматы и шашки), такие участники, играют партию белым цветом) необходимо определить сумму номеров участников пары. При четной сумме хозяином поля является участник с наибольшим номером, при нечетной сумме – участник с меньшим номером.           70

Таким образом, предложенный способ составления таблицы очередности игр можно применять на практике для проведения соревнований по круговой системе при отсутствии таблицы Бергера. Данный способ прошел апробацию при проведении соревнований по мини-футболу, волейболу и шахматам в рамках Спартакиады Казанского юридического института МВД России среди переменного состава с 2021 по 2024 год.

В качестве примера представлена стандартная таблица Бергера при 8 участниках (таб. 2).

Таблица 2 . Таблица очередности игр

Туры / пары 1 2 3 4 1 1 – 8 2 – 7 3 – 6 4 – 5 2 8 – 5 6 – 4 7 – 3 1 – 2 3 2 – 8 3 – 1 4 – 7 5 – 6 4 8 – 6 7 – 5 1 – 4 2 – 3 5 3 – 8 4 – 2 5 – 1 6 – 7 6 8 – 7 1 – 6 2 – 5 3 – 4 7 4 – 8 5 – 3 6 – 2 7 – 1 рисунке 7.

• 1    Все рисунки являются авторскими.