Neural Network Recognizes Fruit Fly's Wing Vibration Sound Based on Hilbert-Huang Transform

Fruit fly harms a variety of fruits and vegetables and damages stems of many plants, especially for Drosophila melanogaster , their feeding habits are most widely. Fruit flies of the same species are very similar in morphology, so it is difficult to distinguish them from their external characteristics. The sound of fruit fly contains much biological information that can reflect species-specific. It has great research value that extracting features of biological information from the sound and monitoring ecological behavior of the fruit fly, so that people can take actions of prevention and treatment to improve the level of agricultural production.

Sivinski et al. studied the male Mediterranean fruit fly and the environment and behavior of their calling song, courtship song and mating song produced [1]. Talyn and Dowse further investigated and discovered that the female fruit fly used the pulse song rather than sine song in the species identification and species mating [2]. Mizrach analyzed the Mediterranean fruit fly’s courtship song, and thought that courtship song can be used to lure and kill fruit fly [3]. Geng et al. determined pulse interval of the courtship song in the six species of Drosophila takahashii [4]. Shao et al. studied the courtship song of the Drosophila nasuta subgroup,

* Corresponding author.

measured time-domain model parameters of the pulse song one by one, and conducted power spectrum analysis [5].

Most scholars at home and abroad analyzed fruit fly’s courtship song in time domain, and less people studied fruit fly’s wing vibration sound (shorted for fruit fly’s sound). Fruit fly’s sound is time-varying, but the time-domain characteristics of the signal can not be sufficient to reflect the specificity of fruit fly species. However, Hilbert-Huang Transform has a very good advantage in dealing with time-varying signals [6], and the method have been successfully applied in underwater acoustic signal processing, fault diagnosis and other fields [7-8].

The paper applies Hilbert-Huang Transform to analyze time-frequency characteristics of fruit fly’s sound, then recognizes two different strains of fruit fly in the same species by BP neural network, and obtains a good recognition result.

• 2.    HHT principle

Hilbert - Huang Transform (shorted for HHT) method consists of two parts: Empirical Mode Decomposition (shorted for EMD) and Hilbert spectrum analysis.

In 1998, Huang et al. proposed the empirical mode decomposition method, the method can decompose the original signal adaptively, and get a series of intrinsic mode functions with frequency from high to low, and the intrinsic mode function is shorted for IMF.

Through the EMD process, original signal   x(t) can be decomposed into n -empirical

(C,C,...,C)                  r modes, 1  2     n , and a residue, n , which can be either the mean trend or a con b stant. Therefore, we

x(t)

can express       as follow:

x ( t ) = T C . ( t ) + rn ( t )^.

I = 1

After performing the Hilbert transform on each IMF component and ignore the residue, we get the corresponding instantaneous amplitude and instantaneous frequency. Therefore, the Hilbert time-frequency expression of the original signal can be expressed as follow:

x ( t ) = Re £ 4 ( t ) exp[ i J ю ( t ) dt ] j = 1

In which, ^{Aj ( t )} indicates the instantaneous amplitude of the complex analytic signal of the j th IMF ^{Cj ( t )} , ^{Ю (t} ) indicates the instantaneous frequency of the j th IMF C^{j (} t ). According to the Hilbert time-frequency expression, the signal’s amplitude and the instantaneous frequency are functions of time. By displaying the amplitude in the time-frequency plane, we can get Hilbert spectrum, ^{H( ю} ,t ) , that is, Hilbert-Huang spectrum (shorted for HH spectrum). HH spectrum not only represents accurately the law of the signal amplitude with changes of the time and frequency, but also to some extent, reflects the distribution of the signal energy in different characteristic scales (time or frequency).

Hilbert marginal spectrum can be further defined by HH spectrum:

T

h( ю ) = J H( to , t ) dt

The marginal spectrum offers a measure of total amplitude (or energy) contribution from each frequency value. It represents the cumulated amplitude over the entire data span in a probabilistic sense.

• 3.    Feature extraction of fruit fly’s sound

Experimental fruit fly, Drosophila melanogaster, are two different strains in the same species, which are respectively red eyes, gray body, long wing, straight bristle mutant fruit fly (labeling 18), and white eyes, gray body, long wing, straight bristle mutant fruit fly (labeling 22).

In paper, Characteristic differences of fruit fly’s sound are smaller among the same strains, and the sound of different strains of fruit fly have larger characteristics differences. We select respectively a sound of fruit fly of 18 labeled and fruit fly of 22 labeled, and do EMD and Hilbert transform, then, get the corresponding HH spectrum of the sound of two strains of fruit fly, shown in Fig. 1, brightness of the point in HH spectrum indicates size of the energy. Three effective features have been extracted in this section: (1) the relative energy of low-frequency band, medium-frequency band and high-frequency band of HH spectrum; (2) time-frequency entropy of HH spectrum. (3) the cumulated amplitude value based on marginal spectrum.

• A.    Feature Extraction of the Relative Energy

In HH spectrum, we set the normalized frequency from 0Hz to 0.1Hz as low-frequency band, the normalized frequency from 0.1Hz to 0.4Hz as medium-frequency band, the normalized frequency from 0.4Hz to 0.5Hz as high-frequency band, and define respectively the energy of low-frequency band ,medium-frequency band and high-frequency band as ^{E l} , ^{E m} , ^{E h} .Therefore, the signal’s total energy E is the sum of ^{E l} , ^{E m} , ^{E h} , and the relative energy of low-frequency band is ^{E lr = E l / E} , the relative energy of medium-frequency band is ^{E mr = E m / E} , the relative energy of high-frequency band is ^{Ehr = Eh / E} .

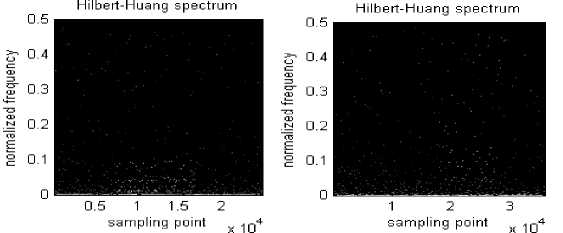
(a) Fruit fly of 18 labeled

(b) Fruit fly of 22 labeled

Fig 1. HH spectrum of the sound of two strains of fruit fly

TABLE I Relative energy of fruit fly’s sound of 18 labeled and fruit fly’s sound of 22 labeled

Relative energy	18 labeled	22 labeled
Low-frequency band	0.4786	0.4339
Medium-frequency band	0.3158	0.3251
High-frequency band	0.2056	0.2410

The energy distribution of low-frequency band is more intensive for the sound of two strains of fruit fly in HH spectrum of Fig. 1. Seen from TABLE I , corresponding to the Fig. 1, the relative energy of low-frequency band of the sound for fruit fly of 18 labeled is higher than the relative energy of low-frequency band of the sound for fruit fly of 22 labeled in HH spectrum, and the relative energy of medium-frequency band and high-frequency band are lower than that of fruit fly of 22 labeled.

• B.    Feature Extraction of Time-frequency Entropy

In information theory, entropy describes the uncertainty of measure. Its mathematical description is as follow: Set the probability of random variable

X(x1, x2,

.,xn)isp(p1,p2,...,pn)

of the probability distribution is defined as:

, then, the information entropy

n

H (P ) = -k£ Pi In Pi i=1

Where, k is an arbitrary constant. If and only if the value of random variable is equal probability, the probability distribution is with the largest uncertainty. Therefore, the probability distribution of the most uncertain has the maximum entropy.

In time-frequency distribution, the energy distribution of the signal is different in different time-frequency bands. Introducing the information entropy to time-frequency distribution, we can describe quantitatively the uniformity of energy changing, and the basic idea of the method is as follow.

We divide the time-frequency plane evenly into N blocks of equal areas. Define the energy of each block as M (1  i,2,-., ^0, entire energy of time-frequency plane is E. So the probability of each time-frequency block

N is q*= Mi' E,

.sq*=1

, use mathematical formula based on information entropy, and the

and * = 1        . Take k ¹

calculation formula of time-frequency entropy is expressed as follow:

N

^s ( q ) =— Z q ln q ■ l = 1

The time-frequency entropy, corresponding to the sound of fruit fly of 18 labeled and 22 labeled in Fig. 1, is showed in TABLE II. Seen from TABLE II, time-frequency entropy of fruit fly of 22 labeled is greater than that of fruit fly of 18 labeled. It indicates that the energy distribution of the sound of fruit fly of 22 labeled in the time-frequency plane is more uniform than that of fruit fly of 18 labeled.

• C.    Feature Extraction of fruit fly’s sound based on marginal spectrum

Marginal spectrum reflects the regulation of amplitude changes with the instantaneous frequency in the whole instantaneous frequency span. Within the range of instantaneous frequency ⁽ ® 1 , ® ² ), we define the cumulated amplitude value of marginal spectrum ^F as follow:

F = Г² h ( ю ) d to                                                                               ⁽⁶⁾

ю

The cumulated amplitude value reflects amplitude distribution of signal within the range corresponding to the instantaneous frequency.

Hilbert marginal spectrums are different for different strains of fruit fly, and the cumulated amplitude values of marginal spectrums have different changes in the same range of the instantaneous frequency. According to experimental analysis, marginal spectrums of the sound of two strains of fruit fly mainly distribute in low-frequency band (0Hz ~ 2000Hz).We obtain marginal spectrums based on the definition of marginal spectrum, as shown in Fig. 2 below, corresponding to HH spectrums of the Fig. 1. Seen from Fig. 2, marginal spectrums of the sound of fruit fly of 18 labeled and 22 labeled concentrate low-frequency band of 0Hz ~ 800Hz, and the differences are larger within 400Hz~800Hz. So we select the frequency range of 400Hz ~ 800Hz and calculate the cumulated amplitude values of marginal spectrum of the sound of two strains of fruit fly, the cumulated amplitude values in 400Hz~800Hz of Fig. 2 are showed in TABLE III

TABLE II Time-frequency entropy of fruit fly’s sound of 18 labeled and fruit fly’s sound of 22 labeled

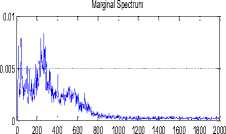
frquency/Hz

(b) Fruit fly of 22 labeled

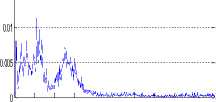
0     200    400    600    800   1000   1200   1400   1600   1800   2000

frquency/Hz

(a) Fruit fly of 18 labeled

Fruit fly type	Time-frequency entropy
18 labeled	1.5539
22 labeled	1.5821

Marginal Spectrum 0.015

Fig 2. Marginal spectrum of the sound of two strains of fruit fly

TABLE III The cumulated amplitude values of marginal spectrum in 400Hz ~ 800Hz of fruit fly’s sound of 18 labeled and fruit fly’s sound of 22 labeled

Fruit fly type	Cumulated amplitude values
18 labeled	0.2575
22 labeled	0.2259

TABLE IV Recognition result of fruit fly of 18 labeled and fruit fly of 22 labeled

Samples and recognition	18 labeled	22 labeled
Training samples	100	100
Testing samples	100	100
Correct recognition samples	86	88
Recognition rate	86%	88%

• 4.    BP neural network

• 5.    Conclusions

The paper applies BP neural network with two hidden layers to recognize the sound of fruit fly of 18 labeled and fruit fly of 22 labeled. The input vector of neural network is the relative energy of HH spectrum, time-frequency entropy and the cumulated amplitude value of marginal spectrum. The input layer is set 5 nodes, the first hidden layer is selected 30 nodes and the second hidden layer is took 15 nodes. The output layer is set two nodes, corresponding to two strains of fruit fly. We select sigmoid function as activation function of each layer and use Levenberg-Marquardt algorithm to train network.

Collecting 200 sound samples of fruit fly of 18 labeled and fruit fly of 22 labeled respectively, of which 100 samples for training set, another 100 samples for testing set, we set the target error of BP network as 0.01, the minimum gradient as ^{10 - 10}.The network converges at the minimum gradient in the 304th step. The recognition result of two strains of fruit fly is showed in TABLE W.

The recognition result demonstrates that the method of the paper can classify fruit fly, and provides new ideas and basis for the identification of different strains of fruit fly.

Fruit fly’s sound contains a wealth of information that can reflect characteristics of different strains of fruit fly in the same species. For the non-stationary of fruit fly’s sound and the advantages of Hilbert-Huang transform in dealing with the non-stationary signal, the paper extracts features that include the relative energy, time-frequency entropy and the cumulated amplitude value of marginal spectrum, then, uses BP neural network to identify two strains of fruit fly, and gets good results. So the method in the paper is feasible and effective. The next work is extracting more effective features for the sound of more different strains of fruit fly through the time-frequency analysis, and classifying a variety of fruit fly and improving recognition rate.

• [1]    J. Sivinski, C. O. Calkins, J. C. Webb. Comparisons of acoustic courtship signals in wild and laboratory reared Mediterranean fruit fly Ceratitis Capitata. Florida Entomol, vol. 72, No. 1, pp. 212-214, 1989.

• [2]    B. C. Talyn, H. B. Dowse. The role of courtship song in sexual selection and species recognition by female Drosophila melanogaster . Animal Behaviour, vol. 68, pp. 1165-1180, 2004.

• [3]    A. Mizrach, A. Hetzroni, M. Mazor, R. W. Mankin, T. Ignat and J. Grinshpun et al. Acoustic trap for female mediterranean fruit flies. American Society of Agricultural Engineers, vol. 48, No. 5, pp. 2017-2022, 2005.

• [4]    Zhencheng Geng, Dingliang Zhu, Yaolai Sun. Study on the courtship song of six species in Drosophila takahashii species subgroup. Acta Genetica Sinica, vol. 16, No. 6, pp. 448-454, 1989.

• [5]    Hongguang Shao, Li Dun, Xianning Zhang, Haijing Yu, Li Xia and Dingliang Zhu et al. Study on the recognition and evolutionary genetics of the courtship song of species in Drosophila nasuta species subgroup. Acta Genetica Sinica, vol. 24, No. 4, pp. 311-321, 1997.

• [6]    N. E. Huang, Zheng Shen, S. R. Long, M. C. Wu, H. H. Shih and Q. Zheng et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A, vol. 454, pp. 903-995, 1998.

• [7]    Wang Feng, Yin Li, Minghong Zhu. Feature extraction and classification of underwater signals based on Hilbert-Huang transform. Applied Acoustics, vol. 26, No. 4, pp. 223 - 230, 2007.

• [8]    Dejie Yu, Zhang Wei, Junsheng Cheng, Yang Yu. Application of time-frequency entropy to gear fault diagnosis based on emd. Journal of Vibration and Shock, vol. 24, No. 5, pp. 26 - 27, 29, 2005.