Неустойчивость решений уравнений Хоффа на графе. Численный эксперимент

Уравнение Хоффа [1]

(A - А₀)щ + u_txx = au + Pu⁵                          (1)

моделирует выпучивание двутавровой балки, находящейся под постоянной нагрузкой. Функция и = и(х, t), (ж, <) € (а, Ь) х R, характеризует отклонение балки от положения и = 0; параметры A, Aq Е R-ь а,Р Е R характеризуют нагрузку и свойства материала балки соответственно. Начально-краевые задачи для уравнения (1) в области (a, b) х R впервые были изучены Н.А. Сидоровым [2] и его учениками [3, 4], причем в [3, 4] был отмечен феномен несущестования решения этих задач при произвольных начальных данных. Изучение множества начальных значений, обеспечивающих существование и единственность решения начально-краевой задачи, было показано в [5]. В [6] показано, что это множество, понимаемое как фазовое пространство уравнения (1), является простым банаховым С°°- многообразием, если ар Е R+- В [7] показано, что если аР Е R-, то фазовое пространство уравнения (1) уже не будет простым многообразием, - оно лежит на сборке Уитни.

Динамику конструкции из двутавровых балок моделируют уравнения Хоффа

(А Xo)ujt 4- Ujtxx — auj + Pv.j,(2)

заданные на конечном связном ориентированном графе G = G(2J, С), где 2J = {Ц} - множество вершин, а (Е = {Е^ - множество ребер, причем каждое ребро Ej имеет длину lj Е R+ и площадь поперечного сечения dj Е R+- В вершинах 23 графа G заданы условия иДОД) = иДО, i) = um(lm,t) = un(ln,t), Ej,Ek E Ea(yi),Em,En E E^^Vi),(3)

' djUj$(O,t^ —      ' dkUkx^lkiip = 0,(4)

E^E^ty^          ЕкеЕУУ)

где через E®^^) обозначено множество ребер с началом (концом) в вершине У, t Е R. Условия (3), (4) обсуждаются, например, в [8]. Нас интересует устойчивость (по Ляпунову)

стационарного решения к = (0,0,..., 0,...) задачи (2) - (4) (см., например, [8]). В [8] было проведено исследование данной задачи при А € [0, Ло]. В результате сформулирована

Теорема 1. (г) При любых а,Р Е ВЦ и А Е [0, Ао) решение О = (0,0,... ,0,...) задачи (2) - (4) асимптотически устойчиво.

(И) При любых а,Р Е R+ а А = Ао решение О = (0,0,... ,0,...) задачи (2) - (4) устойчиво.

Целью данной статьи является проведение численного эксперимента по исследованию неустойчивости стационарного решения и = (0,0,... ,0,...) задачи (2) - (4) в случае, когда А > Ао-

Численный эксперимент

На основе теоретических результатов для подтверждения гипотезы о неустойчивости нулевого решения уравнений Хоффа в системе компьютерной математики Maple 13.0. разработана программа, которая позволяет:

• 1.    По заданным коэффициентам а, ДА, Ао находить приближенное решение для уравнения Хоффа.

• 2.    Получить графическое изображение, которое иллюстрирует неустойчивость нулевого решения при А > Ад.

Для реализации вычислительных алгоритмов программы использовались встроенные функции и стандартные операторы языка программирования Maple 13.0. Для получения графического изображения подключен пакет plots.

Решение задачи (2) - (4) будем искать в виде суммы

т и^ = 52 ^^к, тЕМ,                     (5)

А=1

где {%} - ортонормированное в смысле L^G^ множество собственных функций оператора Штурма - Лиувилля на графе G.

Поскольку обнаружена первая собственная функция оператора Штурма - Лиувилля на графе G

_ 1

/         \ 2

Е^1 (М, \я,ее / при А > Ад можно записать первое приближение решения (2)

и(^ = S^tpi.

Подставим его в (2) и получим уравнение

(А-А0)ДЦ =аДЦ+Д?3Ц).                     (6)

Легко посчитать, что 5(t) = ± /---- “^t —, где С = const.

у —^+е Са

Поскольку нам необходимо провести исследование устойчивости решения (6) в окрестности точки нуль, будем выбирать те постоянные С, для которых |5Ц)| <  е. Например, c№ = ^ + t + c.

Пример 1. Требуется найти численное решение задачи (2) - (4) при заданных коэффициентах а = 5, р = 2, А = 6, Ад = 5 в окрестности (-0,01, 0,01).

П.О. Пивоварова

Результаты приближенного решения задачи (2) - (4) частично приведены в таблице и проиллюстрированы на рисунке.

Таблица

Численное решение уравнения (6) при различных значениях параметров t и С

t	С = 10001,41	С = 10002,41	С = 10003,41
0,1	±0,016486946	±0,016486122	±0,016485298
0,2	±0,027184919	±0,027183559	±0,027182200
0,3	±0,044831741	±0,044829499	±0,044827256
0,4	±0,073966153	±0,073962447	±0,073958742
0,5	±0,122179501	±0,122173357	±0,122167214
0,6	±0,202481359	±0,202471071	±0,202460784
0,7	±0,338640683	±0,338622979	±0,338605277
0,8	±0,581719955	±0,581686939	±0,581653929
0,9	±1,094828649	±1,094747682	±1,094666732
1,012	±19,18107065	±19,04055057	±18,90307561

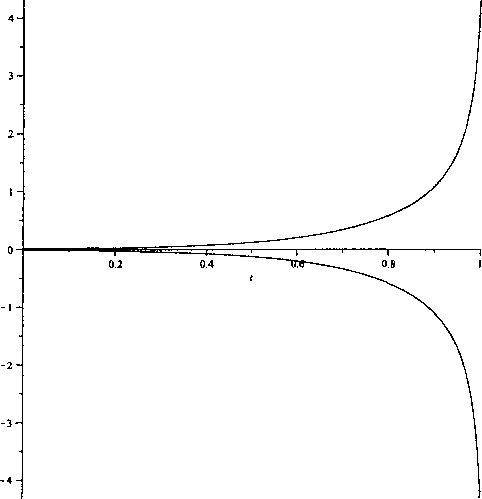
Решения уравнений (6)

при С = 10002,41, С = 10003,41, С = 10004,41, С = 10005,41, С = 10006,41

Замечание 1. Численный эксперимент, проведенный в данной работе, позволяет сделать вывод о неустойчивости нулевого решения задачи (2) - (4) при А > Ло- Поскольку ранее получен результат о устойчивости нулевого решения данной задачи при А € [0, Ао], можно сделать вывод о том что, параметр Ао выступает здесь как предельная нагрузка, при которой конструкция еще устойчива.