New method of crystal material heterogeneity examination

Structure heterogeneity in powder products, for example that of crystal phase and pore distribution, significantly influences their quality and physico-mechanical properties. Among the well known methods of crystal material heterogeneity examination there are metallography of polished sections and X-ray spectroscopy, both intended for qualitative evaluation of phase distribution in products. But these methods are timeconsuming and of no value when one wants to know the degree of heterogeneity or the nature of crystal phase and pore distribution in the bulk of a product.

New method of evaluation of the degree of heterogeneity based on diffractometric analysis of X-ray beam integral intensities surveyed as interference maxima of beam reflections from irradiated samples of different sizes has been developed to assess heterogeneity of phase and pore distribution in the bulk of a crystal or powder material. Thorough analysis of integral intensity dependence on the size of X-ray beam projection on the surface of a sample resulted in the equation permitting to find relative differences between phase concentrations in the samples of different sizes.

New method is mostly advantageous for quantitative evaluation of phase and pore distribution heterogeneity in crystalline, continuous and powder materials as well as for the estimation of powder blending efficiency in multi-phase mixtures. New method compares favourably with other known methods of phase analysis being simple, reliable, permitting to obtain accurate values of phase concentrations and to define the nature of phase and pore distribution both in micro-and macrovolumes of the samples in question.

Apparatus and materials

Experimental investigations on the application of new method of crystal material heterogeneity examination have been carried out with the X-ray apparatus “DRON-2”emitting Cu- K α and Fe- K α radiation [1, 2]. During the experiment both the width and the height of the original beam were varying by “Soller” and collimating slits on the X-ray tube and the counter, respectively, the slits cutting the plane-parallel beam out of X-radiation.

For the experiment, single-phase powders such as calcium aluminates, CaO Al2O3 – CA, CaO 2Al2O3 – CA2, 12CaO 7Al2O3 – C12A7and pressed sintered silicon steel, Fe + 6.68 % Si, were used as well as multi-phase powders made of mixed single-phase powders. Before the experiment calcium aluminates had been atomized by different methods, screened and mixed with a plasticating agent to a putty state and then placed into a quartz cuvette.

S ince t he si li c on st e e l c ontain ing up to 6 . 68 per ce nt of s il ic on wa s e x tre me ly br it tl e at r oom te mpe r a tu r e , the ini t ia l pow der w i t h 130– 150 μ m pa r ti c les ha d be e n pre par e d by a t omi zin g the c a s t s ha ped g r anule s i n the v ib r ating mi ll. T o ob tain t he d isp e rse d powd e r f r ac t ion s wi th l e ss tha n 10 μ m p a r t icle s, the a tomize d powder was sintered in t he open air at 550 °C and atomize d onc e a g a in i n th e v ibr a t ing mill. From t he pre par e d powder s c y li ndr i c a l s a mple s we re p r e s se d und e r th e pr essu r e of 2000 MP a and sint e re d in v a c u um f ur nac e a t the t e mpe ra tu r e o f 1100 °C.

The f in ish e d sa mple s we r e se cur ed on the X-r a y r e fle ct ing g oniome te r per mitt ing t o rotate the s a mple a r oun d it s own a xis , or t he a x i s p e r pendi c ul a r to the p la ne of the r ef lec t ed b e a m, o r th e bot h. Ea c h se par at e c r y stal phase i n th e sample was investigated by X-ray beams with varying wave l engt hs, na m e ly : C A – 2.97 Å and 4.67 Å, CA 2 – 3 . 49 Å and 4 . 44 Å, C 12 A 7 – 4.89 Å and 2.68 Å, Fе + 6.68 % Si – 1 . 42 Å. T o me a sure t he v a lues of int e rf e re nc e ma xi mu m inte g ra l i nt e ns it ies, the pr o f i le s of i nte rf er e n c e lin e s f rom each phase were surveyed step- b y-step at the ang le inter v a l of 0. 01 de g r e e a nd 10 se c e xp osu r e at each step.

Survey conditions

Developing the new method of crystal material heterogeneity examination, the special study has been carried out to determine the influence of beam geometry and survey conditions on the magnitudes of interference maximum integral intensities. For this purpose, the survey of the samples was performed with the help of plane- parallel beam with the provided diaphragm using Bragg – Brentano focusing. “Soller” slits and collimating slits set up on the X-ray tube and the counter confined the incident and the reflected beams in width and height, respectively.

Investigations have shown that it is important to obtain rectangular beam projection with uniform distribution of incident beam energy all over the projection area on the reflecting surface of a sample, so as to increase the effectiveness of the method.

Photographs presented in Fig.1 show that survey conditions strongly influence the intensity of radiation and geometric form of beam projection.

Another important condition is that the rotation of a sample around the axis perpendicular to the plane of beam projection should be of the preset frequency, approximately 1 Hz. Under such rotation the maximum quantity of crystallites forming the whole reciprocal lattice are exposed to the beam, that helps to increase the effectiveness of texture heterogeneity blending in samples.

It should be noted that all the survey conditions mentioned above help to improve the accuracy of quantitative evaluation of interference line integral intensities.

Dependence of relative integral intensity on beam projection size

As a result of experimental investigation, it was found that relative integral intensity of any interference line and the size of plane-parallel beam projection obeyed quadratic dependence (Fig. 2) instead of being directly proportional as many researchers thought. This dependence can be expressed by the following equation:

J h_txb ₀ /J n ₀ xb ₀ = «ф², (1) where J _btxbo is the intensity of interference lines when the width h i of beam projection on the sample surface is varying, and J h _oXbo is the intensity of interference lines when the width h 0 of beam projection and the height b 0 have the base values.

Proportionality factor in Equation (1) is presented by the function а = а(Д^,Д0), (2)

a)

b)

c)

Fig. 1. Photograph of the form of beam projection under different survey conditions: a – with “Soller” slits, when the size of the beam emitted by the X-ray tube is 0.25 x 2 mm and the size of the beam received by the counter is 0.25 x 2 mm; b -with “Soller” slits, when the sizes of the beam are 0.25 x 4 mm and 0.25 x 4 mm, respectively;

c -without “Soller” slits, when the sizes of the beam are 0.25 x 4 mm and 0.28 x 8 mm, respectively

where Δ h is the point beam expansion of the ano de spot, and Д6 is the interference maximum broadening.

If the anode spot point beam expansion falls within the space angle of reciprocal lattice point, then the values of function (2) are close to 1, and if not, then α < 1.

In Fig. 3 the relative integral intensity is plotted against the beam projection size, data being obtained from the experimental investigation of polycrystalline powder samples.

Results of phase heterogeneity magnitude determination

Let us consider the application of the new method to phase heterogeneity magnitude determination by analyzing the three-phase powder mixture containing CA = 15 %, CA 2 = 70% and

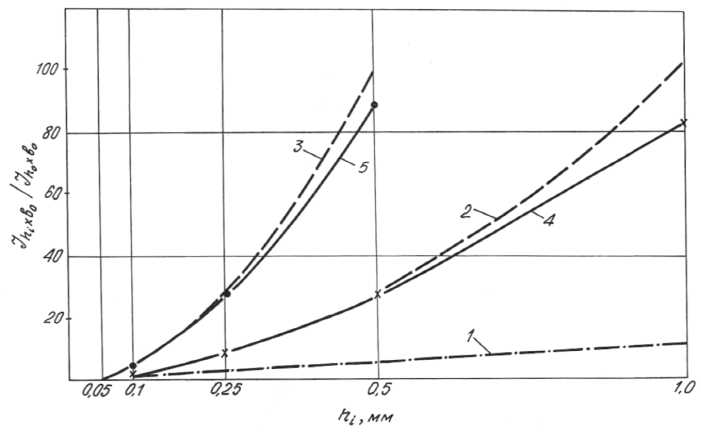
Fig. 2. Plot of the integral intensity J _{h t Xb o} /J _{h o} x _{b o} as a function of beam projection size: 1 – taken from references [3, 4], when h 0 = 0.1 mm; 2– according to the equation (1), when h ₀ = 0.1 mm; 3- according to the equation (1), when h ₀ = 0.05 mm; 4 - experimental, when h ₀ = 0.1 mm; 5 - experimental, when h ₀ = 0.05 mm

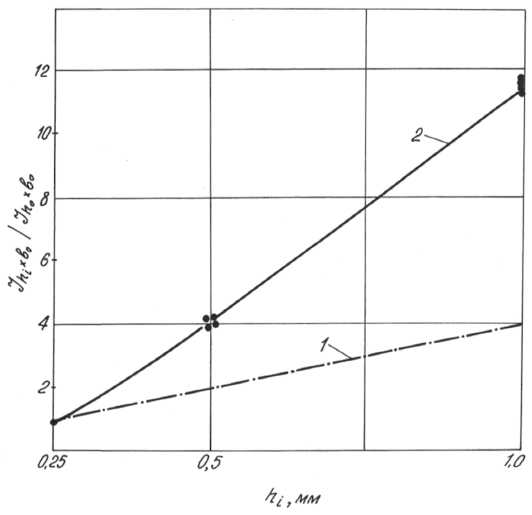
Fig. 3. Plot of the integral intensity J_{h l Xb o}/J _{h o Xb o} as a function of beam projection size h _t for single-phase powders: 1 – taken from references [3, 4]; 2 – experimental, when h ₀ = 0.25 mm

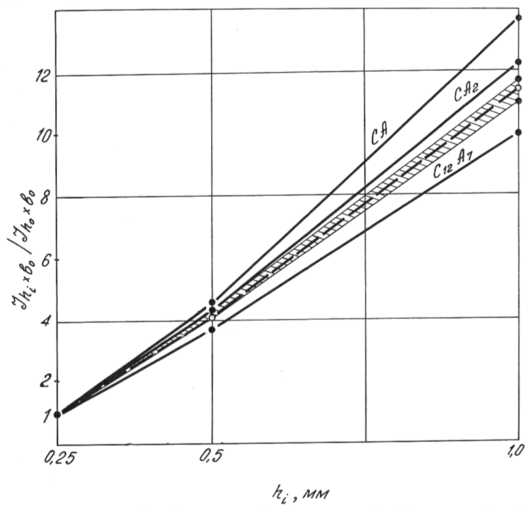
Fig. 4. Plot of the relative integral intensity J_{h l Xb o}/J _{h o Xb o} as a function of beam projection size h i : dotted line refers to powder mixture with uniform phase distribution; shadowed area refers to powder mixture with ±1 % phase heterogeneity; solid line CA corresponds to phase heterogeneity of 4.80 %; solid line CA 2 to phase heterogeneity of 5.25 %; solid line C 12 A 7 to phase heterogeneity of 2.07 %

C 12 A 7 = 15 % calcium aluminates. In Fig. 4 the re lative integral intensity of interference lines is plotted against the width of plane -parallel beam projection derived from the above powder mi x ture examination. The deviation of the curves marked as CA, CA 2 and C 12 A 7 from the base curve (dotted line) shows a non- uniform distrib u tion of the examined crystal phases in the sa mples.

Using the well- known formula for the inte r ference line intensity estimation [3] as the quali tative evaluation of phase distribution heter o geneity in powder samples and varying the width, h i , and the base height, b 0 , of beam projection on the surface of a samp le, we obtain

J h_txb ₀ =J ₀ QaX t h i b ₀ . (3) where /₀ is the density of incident energy at the base height of the beam, Q is the reflectivity of a sample volume unit, X _t is the phase volume fraction exposed to radiation.

When the width of X- ray beam varies from h i to h j , the relative intensity of interference lines can be expressed by the equation

Jhjxbo/Jhtxbo = (тт)2^. (4) l following from Equation (1). The ratio Xj/Xi equals unity if the considered phase is distributed uniformly over the whole sample volume as it is in the case described by the base curve in Fig. 4.

For the sample with non-uniform distribution of the considered phase, the Equation (4) takes the form of

J» l xb o // » o Xb o = (y²(¹+₂ X^l ).

where X 0 is the average phase concentration in homogeneous sample, and Δ Х i is the deviation of phase concentration from its average value in heterogeneous sample.

For the given three phases in the examined powder mixture, relative deviations of concentrations from their average values have been calculated by Equation (5):

CA: ^

X o

C 12 A 7 :

= 0.28; CA₂: ^ 0.075; ² X o

^ = 0.138.

X o

Results of examination of pore distribution heterogeneity

When producing powder articles with the preset porosity, it is necessary most of all to analyze pore distribution heterogeneity. To evaluate the magnitude of pore distribution heterogeneity in samples, pressed and sintered steel powder cylinders containing up to 6.68 percent of silicon were used. Original powders had different fraction compositions which were varied by mixing the normal powder having 130–150 μm fractions with different quantities of dispersed

Porosity heterogeneity in powder samples containing Fe + 6.68 % Si

Table 1

No Samples Original powder fraction composition, % Integral intensity, pulse/s Porosity heterogeneity, % Beam projection size, mm 130–150 μm 10 and less μm 0.25×8 0.50×8 1 100 0 1649 5989 9.2 2 90 10 1721 6431 6.6 3 70 30 1769 6850 3.2 4 50 50 1817 6985 3.9 5 20 80 1841 7047 4.3 Cast Sample 3568 14274 0 phase additions having less than 10 μm fractions. Fraction compositions of the investigated samples are given in Table 1. For comparison, the cast base sample of the same chemical composition was used. All the results concerning the values of interference line integral intensities and pore distribution heterogeneities are also given in Table 1. Analysis of the presented results confirms that the pore distribution heterogeneity is decreasing from 9.2 to 3.2 percent when the content of fine-dispersed fractions in the powder mixture increases from 0 to 30 percent.

Conclusions

• 1.    New X-ray method has been developed to define the heterogeneity of phases and structures in crystal materials using interference maximum integral intensities of different beam projections on the surface of a sample.

• 2.    New technique of diffractometric survey of interference lines has been worked out allowing to achieve the effective blending of texture heterogeneity in a sample and to define qualitative integral intensity values with high degree of reliability and accuracy.

• 3.    Mathematic relationships have been derived to find relative differences between phase

• 4.    New method is advantageous for the evaluation of distribution heterogeneities of pores and phases in crystalline materials as well as for the analysis of the effectiveness of blending for multiphase powder mixtures.

• 5.    No further improvement of the method is necessary to design X-ray tubes with more uniform distribution of the X-radiation energy over the projection area of the original beam.

concentrations in different sample volumes proceeding from X-radiography data.