New P-type and D-type iterative learning control update laws for networked control systems with random data dropouts

For systems that can control an identical work at a limit time in a repetitive manner, iterative learning control (ILC) is an efficient method. In ILC, the information of the previous iteration is used to generate input of the next cycle. Hence, tracking performance improves when the number of iterations increases. The idea of ILC follows from the article [1]. Three essays [2–4] led to further research on ILC. Today, there exists a lot of literature on various topics about ILC, such as [5–15]. ILC is an important field of smart updating law that can be used in practice, for instance, see [16–23].

Besides, network control systems (NCSs) are widely used recently. In NCS, the information can transmit by the communication channels. Therefore, data dropout often occurs in NCSs due to the congestion of network or node failures. The main issue is how good performance can be guaranteed under severe transmission conditions, e.g. data dropouts. For literature about ILC and NCS systems, see the survey [24], which is devoted to ILC for systems with incomplete information.

Note that most of the articles on NCSs, in a way, are not consider the randomness of data dropouts during the proof process of convergence.

In this article, for linear stochastic systems with random data dropout modeled by a Bernoulli random variable, the new P-type and D-type ILC update laws are characterized. We show convergence of the P-type and D-type ILC update laws with random data dropout in the almost sure sense. Randomness of data dropouts is considered. We specify that the convergence conditions of the inputs corresponding to the P-type and D-type ILC update laws for networked control systems are the same. Performance comparison of the P-type and D-type ILC update laws is investigated. In this comparison, we conclude that the P-type ILC update law is more effective than the D-type ILC update law in networked control systems.

The paper is organized as follows. Section 1 gives definition of the system and problem statement. Section 2 presents the P-type ILC update law and its convergence analysis. We study the D-type ILC update law and its convergence analysis in Section 3. In Section 4, we present the illustrative simulation. Finally, Section 5 summarizes the results and draws conclusions.

Let us give some explanations on notations used in the paper. Transposition of a matrix or a vector is denoted by the superscript ^T . We refer to almost sure, infinitely often, independent and identically distributed, with probability one as a.s, i.o, i.i.d and w.p.1, respectively. Finally, ||.|| represents the Euclidean norm.

1.    Definition of System and Problem Statement

Consider the linear system given by the following state-space equations:

X k ( t + 1) = A ( t ) x k ( t ) + B ( t ) u _k ( t ) + p, _k ( t + 1) , y k ( t ) = C (t) X k ( t ) + >Е ( t ) ,

where the index k denotes the number of an iteration, the argument t E [0 , N ] indicates the discrete-time index, x k ( t ) E R ⁿ is the system state, u _k ( t ) E R p is the input signal of the system, and y k ( t ) E R q is the measurement output of the system. The random variables V k ( t ) E R q and ^ _k ( t ) E R n are the measurement and system noises, respectively.

If y d ( t ) , t E [0 , N ] , characterizes the desired output trajectory, then e _k ( t ) = y d ( t ) - y _k ( t ) indicates the tracking error.

In deterministic systems, the general purpose of the control is to construct the ILC algorithm to generate the input such that the output of the system can track the desired output.

In the case of stochastic systems, there exist the measurement and system noises that can not be predicted and eliminated by any algorithm. Therefore, in stochastic systems, we can not expect that y k ( t ) — y d ( t ) ^ 0 V t when k tends to infinity. Hence, in stochastic systems, the control aim is u k ( t ) — u d ( t ) ^ 0 V t when k ^ to .

System (1) is considered under the following assumptions.

A1. As a necessary condition for proving the convergence [25], the matrix C ( t + 1) B ( t ) has the full-column rank Vt.

A2. Since y d ( t ) is realizable, then, for any y d ( t ) , there exist the desired input u d ( t ) and the desired state x _d ( t ) such that

X d ( t + 1) = A ( t ) x d ( t ) + B ( t ) u _d (t) , y d ( t ) = C ( t ) x d ( t ) .

A3. The (i.i.d) sequence {^k(t),k = 1,2,...} is independent of the (i.i.d) sequence {Vk(t),k = 0,1,...}, and both are sequences of white Gaussian noises with zero mean n value such that supkE^^k(t)|2 < to, supkE|Vk(t)|2 < to, lim 1 £ ^k(t)^T(t) = Rt, and n→∞ n k=1              µ

n lim 1 £ Vk(WT(t) = R# a.s, where R* and R# are unknown matrices.

• n →∞ n _{k =1}                            ^µ

A4. The (i.i.d.) sequence of initial states {xk(0)} is such that Exk(0) = xd(0), n lim 1 £ Xk(0)xT(0) = Ro, and supkE|xk(0)||2 < to.

n →∞ ⁿ _{k =1}

Furthermore, { ^ k ( t ) ,k = 0 , 1 ,...}, { x _k (0) ,k = 0 , 1 ,...}, and { ц _к ( t ) ,k = 0 , 1 ,...} are independent of each other.

In this article, without loss of generality, it is assumed that the network exists in the output channel only, and the input channel transmits the data well.

The random data dropout can be simulated with a Bernoulli random variable. For this purpose, a _k ( t ) is introduced as follows:

^a k ^(t) = ^ 0

if y _k ( t ) is well transferred, otherwise.

Let R such that 0 < R <  1 be the probability of successful transfer of the measurement output y k ( t ) for all t and k.

If a k ( t ) = 1 , i.e., y k ( t ) is well transferred, then e _k ( t ) = y d ( t ) — y k ( t ) can be computed for the update. If a k ( t ) = 0 , then no tracking error can be found for the update.

In this article, we present the P-type and D-type ILC update laws for networked control systems. We investigate convergence analysis of the P-type and D-type ILC update laws. This kind of convergence analysis is new. We show that convergence conditions of the inputs related to the P-type and D-type ILC update laws for networked control systems are the same.

2.    P-type ILC Update Law

For discrete-time-varying linear system (1), the P-type ILC update law is as follows:

u k +1 ^(t) = u k ( t + r k G t E k (t + 1) ,

where G t is the learning gain matrix, {r k } is a decreasing sequence that reduces the effect of stochastic noises and satisfies the following conditions:

M       M rk ^ 0,rk > 0,^rk = TO, y^rk < TO. k=1          k=1

Also, { r k } ensures input convergence with zero error in the almost sure sense and also suppresses the effect of stochastic noises when the number of iterations increases.

In (4), we define E k ( t ) as

E k ( t = { 0 k

if a k ( t ) = 1 , if a k ( t ) = 0 .

For a matrix A _mxn , we define the infinity norm ||.| _M as follows:

n

ML

max

1 < i < m

E l a ij l,a ij e A, j =1

where a ij denotes an element of the matrix A .

Now, investigate the convergence analysis of P-type update law (4) by Theorem 1.

Theorem 1. Consider law (4) for updating the input of system (1). If

I I — r k G _t C ( t + 1) B ( t ) l _M <  1 , V I,, then u _k ( t ) ^ u d ( t ) , V t w.p.1, as k ^ to.

Proof. From (4), (6) according to (1), (2), and taking the norm, we have

| A uk +i ( t ) | » < III - r k G t C ( t + 1) B (LL W A u k ( t )L+ + Ь WJIGtllJIC ( t + 1) WJ|B ( t ) W^W A uk ( t ) IL +

+ W r k ILIKIL IK ( t + 1) | » |C ( t + i)WJ| B ( t )WJ|A u k ( t )IL +          _m

+ W r k I»IKILIK ( t + 1) ILWC ( t + 1) ILM ( t ) ILW A x k ( t ) |» +            ^{( 7}

+IK IL IKILIK ( t + 1)IL W C ( t + 1)ILI K ( t + 1)IL+

+ W r k ILIKIL IK ( t + 1)WJK ( t + 1)IL a-s.

According to (1) and (2), we have

«A x k. ( i )IL <  £ ( П | A ( j )IIJ| B WILIIA u k ( i )L+ Ё (й I A ( j HUIE WIL a-s. (8) i =0 j = i +1                                         i =0 j = i

Here П A ( j ) = A ( n ) A ( n - 1) ...A ( i ) , Vn > i and П A ( j ) = I - j = i                                                          j = i

Substituting (8) into (7), we have

| A u- k +i (0 IL <|I - r k G t C ( t +1) B ( t ) I » | A u k (O IL + |r k IIJULIC ( t + 1)IL x x|B ( i ) |J A «k. (OIL + Irk IL |G< ILIE ( t +1)ILI IC ( t +1) I „ |B ( t ) IJ A «k ( t ) IL +

+ |rk ILIIULIE (t^ ILIC ( t+1)ILIIA ( t ) ILE ( .n_iIA ( j ) I.JB ( i)ILx x| A k (0 IL I+ Ir k IL IIULIE ( t +1)IL IC It +1) ILIA ( t)ILx

t t- 1

• *E (П |A ( j ) IL ) IK WIL I+IL IL a     - - ( t +1)ILI IC ( t +1) IL*

• "   ■ ( t + OIL + Ir - 1» a      - . ( t + i)il IK( t + i)IL »-s.

Let us prove that lim | A u _k ( t)|L = 0 . To this end, we use mathematical induction. k →∞        ^∞

Initial step. In (9), let t = 0 :

|A u k ₊ i (0)IL < II I — r k G o C (1) B (0)WJ|A u k (0)| » + |г. | » | G o | » | C (1)ILx x| B (0)| » |A u k (0)|L + I r k ILII G o lLI K (1)|J| C (1)|J| B (0)W » |A u . (0)| » + +|rkIIJIGolUKKILIIC(1)IL ILKILIK(0)IL + IrkIIJIGolLIK(1)l » x    ^{( 7}

x|C (1)||JK (1) IL + |r k IL IIG olLIK (1)IKIK k (1) IL a-s .

Note that |K(1)|L is bounded because a _k (1) is a Bernoulli variable, and its norm is bounded. Also, |K(0)|L , IK(1)IL , and IK(1)IL are bounded because white noises functions K k (0) , K k (1) , and K _k (1) are continuous on [0 , N | . Therefore, concerning lim r _k = k →∞

0 , we conclude that

|r k IL IIG o lLIK (1) I » |C (1)IL l|A (0)ILIK (0)IL ^ 0 w.p.i,

W r k I » |G o | » |a k (1) | » |C (1) | JK(1)IL ^ 0 w.p.i,

W r k W » |G o W » IK (1)IL IK (1)IL ^ 0 w.p.i.

In (i0), Auk (0) is the input error vector, therefore, its norm is bounded. Hence, concerning lim rk = 0, we conclude that k→∞

IrkILIIGolLIL KILL (0)ILIIAuk (0)L ^ 0, ^{| r} k MGoUK ^{(1) |} » ^{| C (1) |}L^{| B (0) |} » ^{| A} u k ⁽⁰⁾ » ^ ⁰ w.p.1 whenk^^.

Let a i = ||I - r k G ₀ C (1) B (0)|| ^ , a i = 0 , i = 2 , 3 , ..., e k = | A u k (0) | _x , and = 0 , under the assumption of Theorem 1, namely, |I — r k G ₀ C (1) B (0) | _x <  1 , and Lemma 1 of the paper [26], from inequality (10), we conclude that lim I A u k (0) | _№ = 0 .

k →∞

Inductive Step. Suppose that lim |Auk(n)|№ = 0 for n = 0,1, ...,t — 1. The purpose k→∞       ∞ is to show that lim ||Auk(n)|№ = 0 for n = t. k→∞

In (9), similar to initial inductive, we have |r k | _M |G _f | _M I a _k ( t + 1) | _x |C ( t +1)11 ^ hk ^(t ■ ^h x ^ ⁰ , w.p.1 ^{and |r} k ILIIGtlLIIO k ^{( t + 1) |}UR k ⁽ t ■ 4 _x 4 0 , w.p.l. Also, t t- 1

note that in |£(П |A(j)IOI4k(i)|x], the number of sum terms is finite because i=0 j=i i = 0,1,...,t, t E |0, N ], where N is the given length of each iteration, hence t t-1

Е(П |A(j ^IJIlMk(i) Ю is bounded. Therefore, i=0 j=i t-1

Ir k I J IG t I JH ( t + 1)I I J IC ( t + 1)L IIA ( t)UE(II(jЮЬ(i)IL] 4 0, w.p.1. i=0 j=i

Taking into account the assumption of induction lim I A u k ( i ) I _x = 0 , Vk, Vi = 0 , 1 , ..., t— k →∞        ^∞

• 1 ,    w.p.1, therefore, we have

Ir k LIG tlL I« k ( t + 1) IJC ( t +1)L IA ( t )L X t - 1 t - 1

^ХЕ(П IM ) IUIB(OILI A u k WIL I 4 0 , w.p.1.

i =0 j = i +1

Since A u k ( t ) is the input error vector, then its norm is bounded. Therefore, since lim r k = o , we conclude that ^Ir k nj G Hji C ⁽ t + ^цладцji^A u kлл ^{4 0} and k →∞

• ^Irk L WGtMok^(t+ ^L^IC(t+ ^1)I^^IB WL ^IAuk WL ^{4 0}w.p.1 ^whenk⁴™.

3.    D-type ILC Update Law

Set ai = II — rkGtC (t + 1)B(t)Ix, a = 0, i = 2, 3, ..., ek = I Auk. (t) Ix, and ^k = 0, taking into account II — rkGtC(t + 1)B(t)Ix < 1 and Lemma 1 of the paper [26], from inequality (9), we conclude that lim I Auk (t)Ix = 0, w.p.1. k→∞       ∞

□

Therefore, P-type ILC update law (4) converge in the almost sure sense. Next section presents the D-type ILC update law and proves its convergence in the almost sure sense.

For system (1), the D-type ILC update law takes the form uk+i(t) = uk (t) + rk Gt |Ek (t + 1) — Ek (t)],                       (11)

where G t is the learning gain matrix, and {r k } is the agent that reduces the effect of stochastic noises as (5). In (11), we indicate E k ( t ) as (6).

Remark 1. Note that this research tries to show that the convergence conditions of the P-type ILC update law and D-type ILC update law for networked control systems are the same, and we present a new way of convergence proof.

Theorem 2. Consider law (11) for updating the input of system (1). If II — r k G t C ( t + 1) B ( t)||_x<  1 , Vt , then u _k ( t ) 4 u _d ( t ) , Vt w.p.1, as k 4 to.

Proof. Due to (6), from (11) we have uk+1(t) — uk (t)+ rkGt [Ek (t+1)-Ek (t)] — uk (t) + rkGt [ak (t+1)ek (t+1) — ak (t)ek (t)]. (12)

Therefore, we have

IIAuwWL A HI - r k G t C ( t + 1) B ( t ) H » H A u k ( t ) I » + llr k I » IGLHC ( t +1)M x||B ( t )||»||A u _fe ( t ) H _ + Hr k LHGtLHa k ( t +1) H _ HC ( t+^LIB ( t ) H _ H ^ U k ( t)IU+ + H r k I » HG tL IL ( t +1)L HC ( t +1)L HA ( t ) H _ Ё( П IW)HJ IB ( i ) IU x i =0 j = i +1

x||A u k ( i )!_MH r k IU H G tL H a k ( t +1)IU H C ( t +1)IU H A ( t )L [ E ( П H A ( j )L)x t - 1 t - 1         i = ⁰ j = i                     (13)

xH^ k ( i )L+ Hr k LH G t HJI a k ( t )L HC ( t )L[ E ( П M(j )IU) Hb LL x i =0 j = i +1

xIAuk(i)I»] + IrkI»IGtI»Iak(t)UCWILE,(П IA(j)I») I^kWIIJ+ + IrkI» HGtL Iak(t + 1)I» IC(t + 1)I» IM + Al» + IrkI» HGtL x x Iak(t + 1)I» I^k(t + 1)L + IrkI» IGtI» Iak(t)I» I^k(t)La.s.

Using mathematical induction and taking into account the proof of Theorem 1, we conclude that lim H A u _k ( t ) I » — 0 , w.p.1.

k ^»                                                            и

Therefore, we investigated the convergence of the D-type ILC update law. Also, we showed that the convergence conditions of both P-type and D-type ILC update laws for networked control systems are the same.

4.    Illustrative Simulations

This section shows an example. We compare performance of the P-type and D-type ILC update laws. The dynamic of a linear system is as follows:

X 1 ( t + 1) — X 1 ( t ) + 0 , 0100 x 2 ( t ) + L 1 ( t + 1) ,

X 2 ( t + 1) — X 2 ( t ) - 1 , 3421 x 2 ( t ) + 0 , 0378 u ( t ) + ^( t + 1) ,             (14)

У(t) — x2(t) + L(t), where x1 (t), x2(t) are the states of the system, u(t) is the input of the system, y(t) is the output of the system. The whole iteration length is 1 s, i.e. N — 100. The desired output is yd(t) — 3(sin(20,) + 1 — cos(20)), 0 A t A 100. The initial input is u0(t) — 0, Vt. Also, Q (t), l2 (t) and l(t) are the system and measurement noises of the system, respectively, that have normal distribution N(0, 0, 022).

Let us illustrate performance of the P-type and D-type ILC update laws. Also, we show the advantage of the P-type ILC update law compared with the D-type ILC update law.

First, we investigate the convergence properties of the D-type ILC update law and the P-type ILC update law. The probability of successful transfer of the output is A0. , i.e. R — 0 , 9 . We consider the learning gain matrix to be L t — 50 , and assume that the agent

( k +10) ■

that reduces the effect of stochastic noises is r _k —

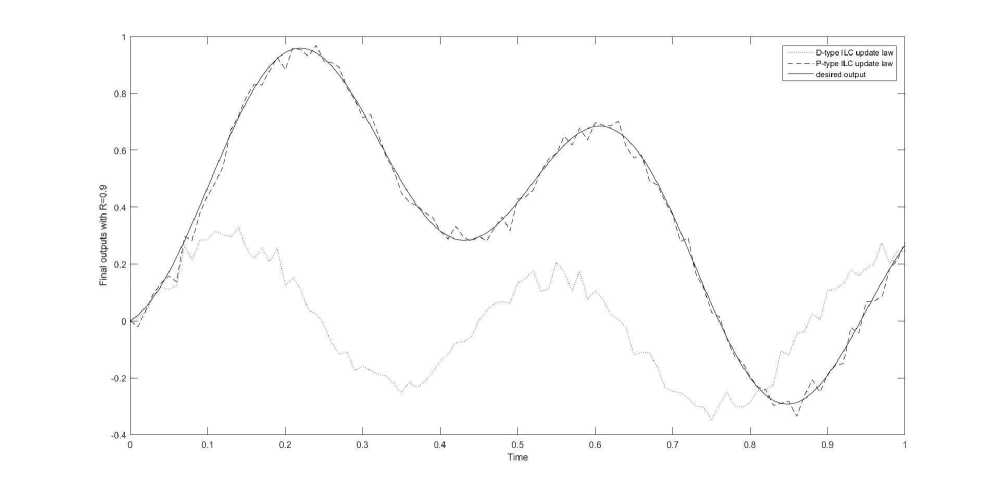
Fig. 1 . Outputs of the P-type and D-type ILC update laws at the final iteration: R=0,9

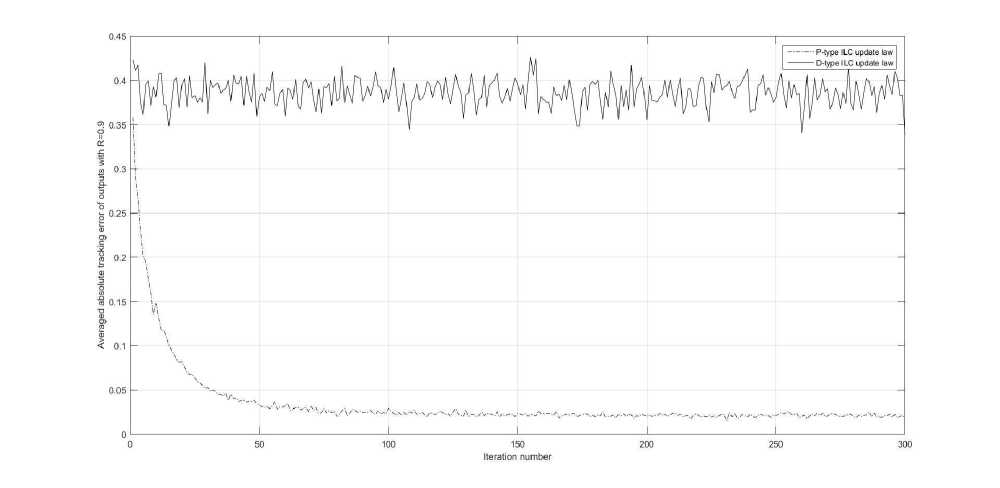
Fig. 2 . The average absolute tracking error of the outputs of the P-type and D-type ILC update laws along the iteration axis, R=0,9

Fig. 1 shows the final outputs of the P-type and D-type ILC update laws, where green, red, and blue curves indicate the desired output, the final outputs of the P-type and D-type ILC update laws, respectively. According to Fig. 1, the curves of the output of the P-type ILC update law and the desired output almost coincide, while the curves of the output of the D-type ILC update law and the desired output do not coincide. Therefore, the P-type ILC update law converges to the desired output when R = 0 , 9 , while the D-type ILC update law can not quickly converge to the desired output when R = 0 , 9 .

We plot the average absolute tracking error along the iteration axis in Fig. 2. The average absolute tracking error is determined by ||ek ||№

(tE lb(t) l jj

N

in the k-th

iteration. Obviously, there exists a significant difference regarding performance between

the two algorithms.

Although the probability of successful transmissions in the output channel is high, performances of the P-type and D-type ILC update laws are different, even if there are no data dropouts. For a more thorough study of the P-type and D-type ILC update laws, we consider different probabilities of data dropout. In order to specify performance of the algorithms with different probabilities of data dropout, we compare the P-type and D-type ILC update laws. We run algorithms in 300 iterations.

We present the average absolute tracking error of the D-type ILC update law concerning different dropout probabilities, R = 0 , 9; 0 , 7; 0 , 5 , and 0 , 3 in Fig. 3. Obviously, under all probabilities of data dropout, the average absolute tracking errors of the D-type ILC update law along the iteration axis are not decreasing almost uniformly, and there exist a lot of error variations.

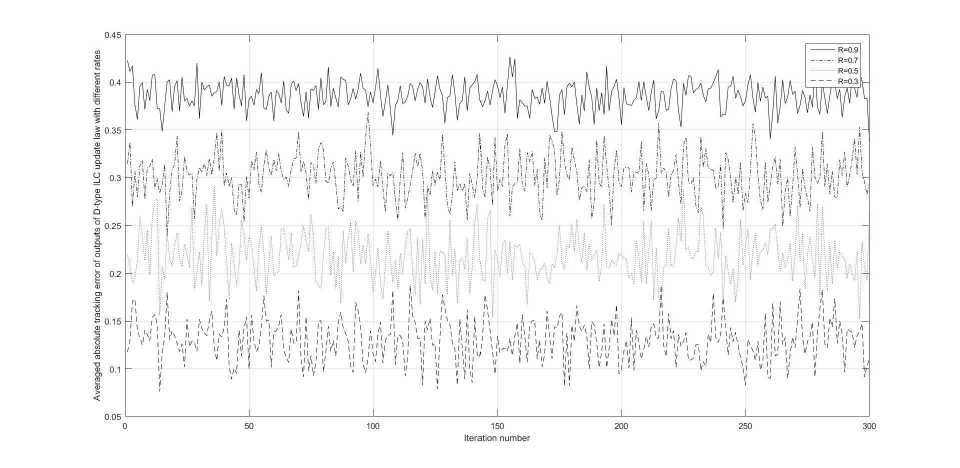
Fig. 3 . The average absolute tracking error of the outputs of the D-type ILC update law with R = 0 , 9; 0 , 7; 0 , 5 and 0 , 3

Finally, the case of the P-type ILC update law is illustrated in Fig. 4. Under different probabilities of data dropout, the average absolute tracking errors of the P-type ILC update law are more overlap than those in the case of the D-type ILC update law, because there exists a small number of error variations in the P-type ILC update law. On the contrary, there are a lot of error variations in the D-type ILC update law.

Conclusion

In this paper, we present new P-type and D-type ILC update laws for stochastic linear systems with random data dropout. We model random data dropouts by a Bernoulli random variable. Also, we investigate the convergence of the P-type and D-type ILC update laws in the almost sure sense. We show that the convergence conditions of the

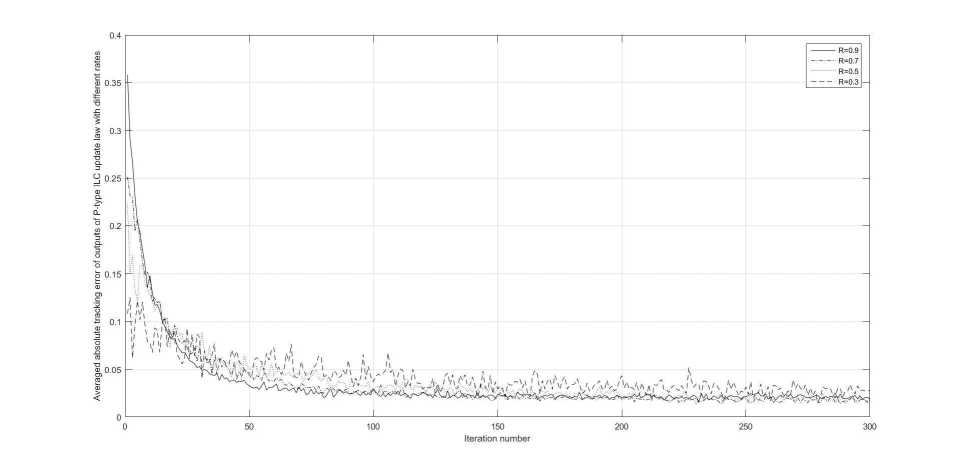
Fig. 4 . The average absolute tracking error of the outputs of the P-type ILC update law with R = 0 , 9; 0 , 7; 0 , 5 and 0 , 3

inputs corresponding to the P-type and D-type ILC update laws for networked control systems are the same. In addition, we investigate performance comparison of the P-type and D-type ILC update laws. In this comparison, we conclude that the P-type ILC update law is more effective than the D-type ILC update law in networked control systems.