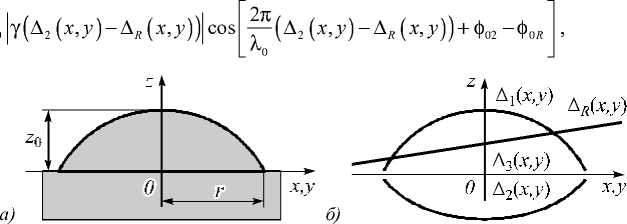
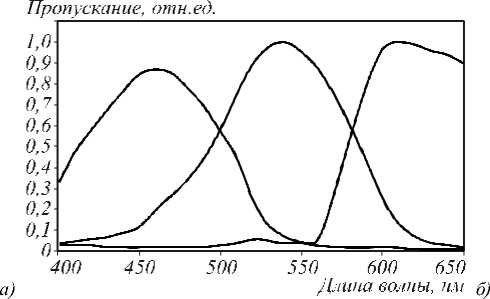
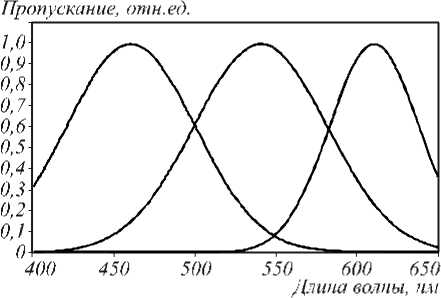
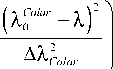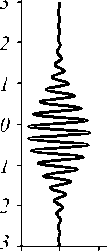Низкокогерентная интерферометрия слоистых структур в полихроматическом свете с цифровой записью и обработкой интерферограмм
Автор: Лычагов Владислав Валерьевич, Рябухо Владимир Петрович, Кальянов Александр Леонтьевич, Смирнов Илья Владимирович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 4 т.34, 2010 года.
Бесплатный доступ
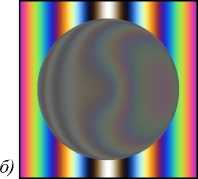
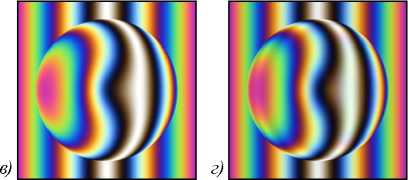
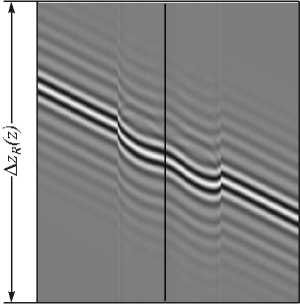
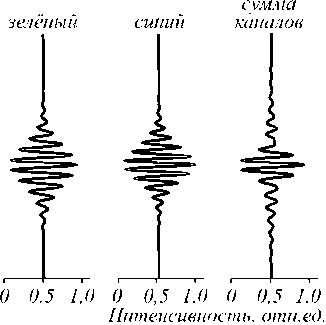
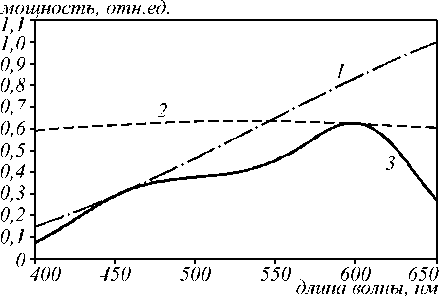
Рассматриваются процессы формирования и цифровой записи интерференционных картин, образующихся в полихроматическом свете при интерференционном контроле микрорельефа поверхности объектов со слоистой объёмной структурой. Получены выражения для распределения интенсивности света в интерференционной картине в зависимости от формы поверхности и структуры объекта с учётом спектральных свойств элементов матричного фотоприёмника. Выполнены численное моделирование интерференционных процессов в полихроматическом свете и экспериментальная запись цифровых интерферограмм микрообъектов в микроинтерферометре Линника с использованием источника белого света. Показаны соответствие рассчитанных и экспериментальных интерферограмм и возможность решения прямой задачи численного моделирования интерференционных картин.
Низкокогерентная интерферометрия, когерентность, тонкие плёнки, цифровая обработка изображений, интерференционная микроскопия
Короткий адрес: https://sciup.org/14058970
IDR: 14058970
Текст научной статьи Низкокогерентная интерферометрия слоистых структур в полихроматическом свете с цифровой записью и обработкой интерферограмм
Явление интерференции достаточно широко используется для исследования формы и микроструктуры слоистых сред. Одним из наиболее эффективных направлений интерференционных измерений можно считать интерферометрию тонких плёнок [1-3]. В отношении традиционных аналоговых способов наблюдения, регистрации и обработки интерферометрических данных в значительной мере разработаны вопросы, касающиеся формирования интерференционных картин тонкими плёнками [2-3], изучены вопросы оптимальных условий освещения контролируемых объектов и наблюдения интерференционных картин, в том числе в поляризованном свете [4].
В связи с развитием цифровых технологий регистрации и обработки оптических сигналов и изображений в последнее время становится актуальным соответствующее развитие описательного аппарата, позволяющего анализировать интерференционные картины в дискретных системах формирования изображений [5-9]. Использование современных цифровых систем регистрации, обработки и визуализации интерференционных картин требует учёта спектральных и пространственных параметров матричных фотодетекторов при качественном и количественном анализе интерферограмм, особенно цветных интерферограмм, формируемых в белом свете.
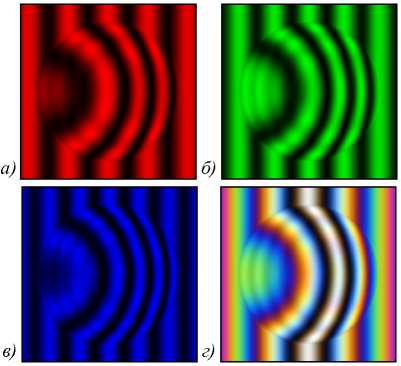
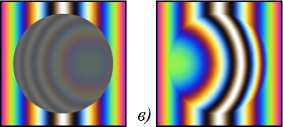
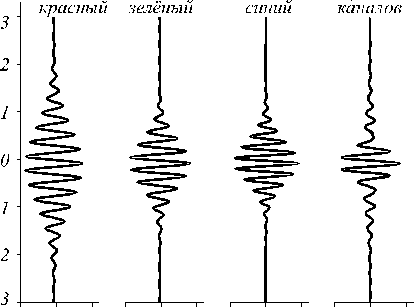
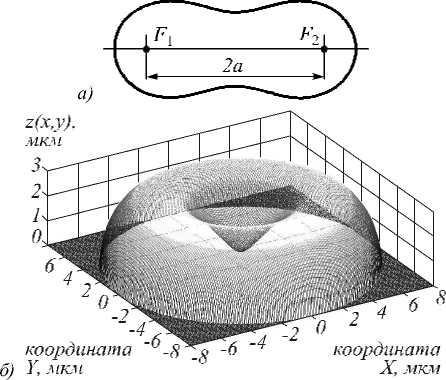
В настоящей работе осуществлена попытка изложить теорию формирования изображения на выходе интерференционного микроскопа с цифровой регистрацией, построенного на базе микроинтерферометра Линника. Рассматриваемая система использовалась нами ранее для исследования внутренней структуры прозрачных слоисты х объектов [10-11] – высушенных капель плазмы биологических жидкостей и эритроцитов в сухом мазке крови. В силу специфики выбранного объекта исследований расшифровка полученны х от них интерферограмм яв- ляется весьма сложной, неоднозначной задачей. Причиной тому служит как сложность пространственной структуры, так и большое число степеней свободы, изначально присущих живым системам и приводящих к значительному изменению их свойств даже при н езначительном изменении исходных параметров. Один из возможных вариантов снятия неопределённости при интерпретации интерферометрических данных – сравнени е экспериментальных интерферограмм с результатом теоретического численного расчёта и выявление общих черт, позволяющих единственно правильным образом классифицировать наблюдаемые в эксперименте сигналы и изображения.
Цель настоящей работы заключалась в получении аналитических выражений для компьютерного моделирования интерференционны х картин в белом свете с учётом спектральных свойств пиксельной структуры регистрирующей матрицы.
Интерференционная микроскопия
Метод интерференционной микроскопии является распространённым и доступным инструментом для исследования оптических свойств и микроструктуры слоистых объектов [10-13]. Микроинтерферометр Линника (рис. 1) служит примером одной из возможных реализаций этого метода. Однако представленная в работе теоретическая модель интерференционного сигнала применима для описания любого интерференционного микроскопа.
В методе интерференционной микроскопии на поле микроскопического изображения объекта накладывается когерентное ему, отражённое от опорного зеркала опорное световое поле. Межд у предметным световым полем и опорным возникает интерференция. Вид интерференционной картины зависит как от характ ера рельефа поверхности прозрачного объекта, так и от его внутренней структуры. Интерферировать с опорным полем может не только волна, отражённая от поверхности объекта, но и волна, отражённая от любой оптической неоднородности внутри самого объекта. Однако в случае, если в структуре объекта присутствуют слои с оптической толщиной меньше половины продольной длины когерентности используемого излучения или сам объект представляет собой тонкую плёнку, интерференционная картина возникает даже в отсутствие опорной волны. Интерферировать будут волны, отражённые от границ слоя или плёнки. В этом случае использование опорной волны существенно усложняет формирующуюся интерференционную картину за счёт одновременной инт ерферен-ции нескольких взаимнокогерентных волн или наложения нескольких интерференционных картин.
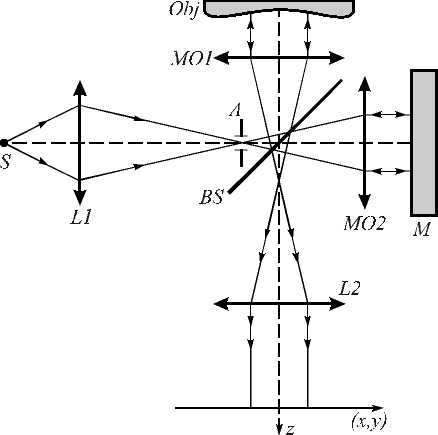
Рис. 1. Оптическая схема микроинтерферометра Линника с цифровой регистрацией сигнала:
S – протяжённый источник белого света,
-
L1, L2 – линзы, A – апертурная диафрагма,
MO1, MO2 – микрообъективы, BS – светоделитель, Obj – объект, M – зеркало
Если объект представляет собой тонкую плёнку с незначительным изменени ем рельефа поверхности, то толщина этой плёнки может быть измерена по цветовой окраске интерференционных полос равной толщины при использовании источника белого света в отсутствие опорного пучка. Однако если объект имеет неоднородную структуру и изменение его оптической толщины превышает половину продольной длины когерентности используемого источника белого света, измерение его геометрических характеристик в такой схеме становится невозможным без использования опорного пучка света.
Одновременное присутстви е в слоистом объекте как тонких слоёв, в которых возникают интерференционные полосы равной толщины, так и относительно толстых слоёв, визуализация которых треб у-ет наличия опорной волны, приводит к необходимости использования универсального инструмента, которым может служить интерференционная микроскопия, и соответствующего теоретического аппарата для послед ующего анализа результатов интерференционного эксперимента.
Формирование интерференционных картин в частично когерентном свете
Белый свет в практических случаях всегда частично когерентен и в пространств енном, и во временном отношениях. Источники белого света имеют протяжённый угловой размер 2 6 , что предопределяет конечный радиус поперечной пространственной когерентности р±~Х0/ 2 6 [14,15], меньший апертуры пучка, и конечную длину продольной пространственной когерентности р„ ~ 2 X 0 /б 2 , где X 0 — длина волны [16,17]. Ширина частотного спектра Ato белого света сравнима с его центральной частотой to 0, Ato ~ to 0, что даёт исключительно малую длину временной когерентности такого оптического поля l c = 2 п с / Ato = X 0 /AX = 1 мкм, где c – скорость света, AX - ширина спектра в шкале длин волн.
Для наблюдения эффектов интерференции в таком свете в интерферометрах с амплитудным делением исходного волнового поля источника необходимо, чтобы разделённые волновые поля накладывались в пространстве на выходе интерферометра с взаимным поперечным пространственным сдвигом ( A x , A y ) << р± , продольным сдвигом A z << р„ и оптической разностью хода A << l c . В этом случае интерферирующие волновые поля возбуждают в каждой точке области их наложения взаимнокогерентные колебания. Если взаимный пространственный сдвиг ( A x , A y , A z ) превышает радиус поперечной или длину продольной пространственной когерентности волнового поля, то колебания становятся взаимно некогерентными и интерференция этих колебаний исчезает. В промежуточном случае имеет место интерференция частично когерентных колебаний.
Интенсивность результирующ его (суммарного) волнового поля в некоторой плоскости наблюдения на выходе интерферометра может быть записана с помощью следующего выражения:
I ( x , y ) = ^| г 1 ( to ) E 0 ( x , y , z , t ) + r ( to ) E 0 ( x -A x , y -A y , z -A z , t -A/ c )| J = r 2 ( to )^ E 0 ( x , y , z , t )| 2^ + r 2 2 ( to )^ E 0 ( x -A x , y -A y , z -A z , t -A/ c )| 2^ + + 2 r 1 ( to ) r 2 ( to ) Re ^ E 0 ( x , y , z , t ) E 0* ( x -A x , y -A y , z -A z , t -A/ c )^ = = r 2 ( to ) 1 0 + r 2 2 ( to ) 1 0 + 2 r 1 ( to ) r 2 ( to ) Re Г ( A x , A y , A z , A ) ,
где r 1 ( to ) и r 2 ( to ) - амплитудные коэффициенты, определяющие изменение исходного поля E 0 ( x , y , z , t ) при его распространении в плечах интерферометра, r ( A x , A y , Az , А ) = ^ E 0 ( x , y , z , t ) х х E 0 * ( x -A x , y -A y , z-Az , t -A/ c )^ - функция пространственно-временной когерентности исходного оптического поля с интенсивностью I 0 в плоскости наблюдения интерференционной картины. В общем случае амплитуда каждой из отражённых волн б удет зависеть от частоты (или длины волны), но, не внося существенных погрешностей, в первом приближении можно считать все коэффициенты отражения константами: r 1 ( to ) = r 1 , r 2 ( to ) = r 2 ит.д.
Требование
(
A
x
,
A
y
)
<<р±
,
A
z
< и A<< lc определяет близкое к максимальному значени е модуля нормированной ф ункции – степени когерентности |y(Ax, Ay, Az, A)|=|r(Ax, Ay, Az, A)| J10 и наблюдение интерференционной картины или сигнала с наибольшим (практически единичным при Г = r22) контрастом полос. В интерферометрии с делением по амплитуде и с использованием протяжённых источников белого света достаточно просто реализовать условия (Ax,Ay)<<р±, Az<<рмдля источников с относительно малыми угловыми размерами 26 и наблюдением интерференции в области пространственной локализации интерференционных полос, где Ax = 0, Ay = 0, Az = 0 . В задачах интерференционного определения параметров микрорельефа поверхности и слоистой структуры объектов область локализации изображения объекта должна пересекаться с областью локализации интерференционных полос. При выполнении условий (Ax, Ay )<<р±, Az<< Рп в функции пространственно-временной когерентности Г (Ax, Ay, Az, A) остаётся только зависимость от разности хода A. Поэтому в уравнении (1) остаётся зависимость интерференционной картины только от функции временной когерентности r(A) волнового поля: I (x, y) = r210 + r210 + 2rx r2 Re r(A) = (2K / (2) = ri210 + r2210 + 2riГ210 |Y(A)| cos I ^“A(x, y) + aI , V % ) где y(A) = r(A)/10 - степень временной когерентности, a = arg Y (A) - 2 nA/ % 0. Уравнение (2) определяет изменение интенсивности в интерференционной картине в зависимости от разности хода A ( x, y) для различных точек плоскости наблюдения ( x, y) . При A > lc взаимная когерентность колебаний складываемых волн нарушается, |y(A)| = 0, и интерференционные полосы имеют практически нулевой контраст. Если исследуется однослойный объект – плёнка на поверхности подложки, то объектное поле состоит из суммы двух волновых полей, отражённых двумя границами раздела сред. Эти поля могут интерферировать, если оптическая толщина слоя nd меньше половины длины временной когерентности, nd< lc/2. Интенсивность возникающей интерференционной картины будет определяться уравнением (2). При большей толщине плёнки необходимо использовать опорную волну – объект исследуют с помощью интерферометра. В этом случае на выходе интерферометра имеет место наложение трёх волн для однослойного объекта, четырёх – для двухслойного и т.д. Анализ интерференции трёх и более волн удобнее проводить с использованием оптической разности хода каждой волны, включая опорное поле, относительно некоторой реальной поверхности, которую можно назвать отсчётной или также опорной. Положение этой поверхности, часто – плоскости, определяется в зависимости от решаемой задачи. В частности, при интерференционном контроле слоистого объекта – плёнки на плоской поверхности подложки, удобно выбрать в качестве отсчётной поверхность подложки. Если стоит задача определения п араметров неоднородности или дефектов поверхности, размеры которых меньше поперечных размеров подложки, можно рассмотреть две независимые области – непосредственно саму область локализации неоднородности (или плёнки) и свободную поверхность подложки. Для этого необходимо ввести в рассмотрение дополнительное поле, отражённое поверхностью подложки. В соответствии с условиями, определёнными выше, оптическая разность хода волны, отражённой от этой поверхности, б удет равна нулю. В этом случае за пределами неоднородности достаточно рассмотреть результат интерференции только двух волн – опорной и отражённой от подложки. Распределение интенсивности в интерференционной картине б удет описываться выражением (2). На рис. 2 схематично показано сечение слоистого объекта – локальной плёнки на подложке, и возможные графики для разностей хода трёх объектных A1 (x, y), A2(x, y) A3 (x, y) и опорной AR (x, y) волн относительно отсчётной плоскости – верхней поверхности подложки. Для каждой из этих волн можно записать опти- ческую разность хода, отсчитываемую от поверхно- сти подложки, в след ующем виде: Ai (x,y) =-2z(x,y) A2(x, y) = -2 z (x, y) + 2 nz (x, y) A3 (x, y )= 0 AR (x, y) = 2ax + 2вy + 2AzR, где A1 (x, у) - оптическая разность хода волны, отражённой от верхней поверхности неоднородности, А2 (x, у) - оптическая разность хода волны, отражённой от поверхности подложки, расположенной под неоднородностью, A3 (x, у) - оптическая разность хода волны, отражённой от поверхности подложки, находящейся за пределами неоднородности, АR (x, у) -разность хода волны, отражённой от опорного зеркала, n - показатель преломления неоднородности, а, в -углы наклона опорного зеркала по отношению к осям x и у, соответственно, 2AzR - начальная разность хода опорной волны, задаваемая продольным смещением опорного зеркала вдоль оптической оси, z ( x, у) – профиль поверхности плёнки. Для волновых полей, участвующих в образовании интерференционной картины, можем записать выражения: Ei (x, у, z, t) = = r exp(iф01) Eо (x,у,z,t-Ai (x,у)/c), E2(x, у, z, t ) = = r exp (iф02) Eо (x, у, z, t -A2 (x, у)/c), E3 (x, у, z, t ) = = r3 exp(iф03) E0 (x,у,z,t), ER (x, у, z, t ) = = rRexP (iфоr ) E0 (x, у,z, t-Ar (x, у)/c), где ф01, ф02, ф03 и ф0R - фазовые сдвиги волн при их отражении от соответствующих поверхностей. В соответствии с вышеоговоренной моделью интерференции волн интенсивность в области локализации неоднородности будет определяться суперпозицией трёх волн: I(x,у) ~/E1 (x,у,z, t) + E2(x,у,z,t) + ER (x,у,z,t)|2^ = r1210+ r2210+ rR210+ +2rir210 I Y(A1 ( x, у )-A2 ( x, у ))| cos +2rirRIc| Y(A1 ( x, у )-AR ( x, у ))| cos ■2^1 ( x, у )-A2 ( x, у )) + ф01 -ф02 . A0 + ■2^1 (x,у)-Ar (x,у)) + ф01 -ф0r .A 0 +2 r2 rRI( Рис. 2. Профиль поверхности исследуемого объ екта (а) и соответствующее ему распределение оптической разности хода волн, отражённых границами раздела (б) а распределение интенсивности вне области локализации неоднородности будет определяться выражением (2), в котором аргумент функции временной когерентности Δ будет представлять собой разность оптических путей ΔR(x,y)-Δ3(x,y)=ΔR(x,y), а постоянный фазовый набег в аргументе косинуса равен ф03- ф0R . В (5) четвёртое слагаемое определяет интерференцию двух объектных волн, отражённы х границами плёнки; пятое слагаемое – интерференцию объектной волны, отражённой верхней поверхностью плёнки, с опорной волной; ш естое слагаемое – интерференцию объектной волны, отражённой нижней поверхностью плёнки, с опорной волной. Модуль степени когерентности |γ(Δ)| в этих слагаемых определяет контраст интерференционных полос. При Δ>lс интерференция соответствующей пары волн исчезает. Для максимума контраста интерференции объектной волны, отражённой верхней поверхностью плёнки, необходимо, чтобы A1 = AR , а для второй поверхности плёнки A2 = AR , что обеспечивается соответствующим продольным положением опорного зеркала интерферометра. С методологической точки зрения выражение (5) показывает, что картину инт ерференции трёх волн можно представить в виде суммы трёх отдельных интерференционных картин, возникающих в результате наложения и интерференции отдельных пар волн. Это важно и для расчёта и компьютерного моделирования интерференционных картин, образующихся при многослойном объекте, когда требуется определить вклад многих слоёв объекта в результирующую картину интерференционных полос. Выражения (2) и (5) позволяют смоделировать интерференционную картину для объекта с заданными оптическими параметрами – толщиной и показателем преломления, в широкополосном излучении и представить эту картину в градациях серого. Для этого необходимо задать среднюю длину волны Х0 и в явном виде выражение для степени времен ной когерентности у(А), которое может быть представлено, в частности, в форме действительной гауссовой функции: у(А) = exp А lc где длина временной когерентности lc определяется шириной спектрального интервала АХ , lc = Х20 /АХ. Для белого света можно принять lc = 1 мкм, Х0 = 0,55 мкм [18]. Спектральное представление уравнения интерференции Для теоретического анализа процессов формирования интерференционных картин в полихроматическом излучении и последующей регистрации в дискретных системах записи изображений особый интерес представляет взаимное влияние спектральных свойств входящих в интерференционную систему элементов. В первую очередь следует учитывать спектральный состав излучения используемого источника и спектральные кривые чувствительности регистрирующей аппаратуры. Влияние этих параметров может быть опосредованно введено в уравнения (2) и (5) путём задания соответствующей функции когерентности Г(А). Второй значимый фактор – необходимость учёта спектральных свойств самого исследуемого объекта, главным образом его дисперсионных свойств, так как в большинстве практически значимых применений исследуемый объект демонстрирует существенную зависимость показателя преломления от частоты зондирующего излучения, что особенно актуально в случае использования широкополосного полихроматического излучения. Во всех упомянутых случаях необходимо использовать спектральное представление интерферирующих полей и самого интерференционного уравнения, позволяющего в явном виде оперировать со спектром излучения источника, спектром пропускания фильтров регистрирующей матрицы фотоприёмников, спектром отражения исслед уемого объекта, его дисперсионной зависимостью и т.д. С использованием спектральных представлений для интерферирующих полей можно записать следующие выражения: Р M У X У E1(t, x, У) = I nrexp (i Ф01) g (o)x 0 x exp icol t — А1 (x, У) c do, P M У X У E2(t, x, y) = I F2exp ( i Ф02 ) g (°)x x exp iol t — А 2 ( x, У ) c do, Eз( t, x, y) = = fr3 exp (iФоз)g(o) exp [iot]do, 0 Г M у x у ER(t, x, У) = rR I , exp ( i Фо R ) g (O)X x exp iol t — А R ( x, У ) c do, где g (o) - амплитудный спектр освещающего поля. Для распределения интенсивности в интерференционном изображении можно записать выражение: lObec (x, y) 'Ez (x, y )| 2^ = ^E 1 (t, x, y) + E2(t, x, y) + ER (t, x, y )|2^ = MM M = J Г12g2 (o) do+ J r22g2 (o) do+ rR2 J g2 (o) do+ 00 0 M +2Re jexp ( i (ф01 —ф02 )) J l 0 r1 r2 g 2 (o) exp i °(А1 ( x, у )—А2 ( x, у )) dor + c I M +2Re ^R exp ( i (ф01 —ф0 R )) J r1 g2(o) exp i o (А1 ( x , y )—АR ( x , y )) do+ M M +2Re j rR exp ( i (ф02 —ф0 R )) J r2 g2 (o) exp i-(А R ( x, y )—А 2 ( x, y )) do[, I _ c _l где угловые скобки … означают усреднение по вре- мени, определяемое конечным временем срабатывания фотоприёмника. Для вывода выражения (8) использовано приближение для дельта-функции Дирака ^ exp [ i (o—o’) t ]^ = 1 T = lim— Г exp Г i (o—o') 11 dt = 2n8(o—o’), T^M T J -I 10 и применено фильтрующее действие этой ф ункци и [19-20]. Выражение (8), также как и (5), показывает, что результирующая картина интерференции многих волн может быть представлена в виде суммы интерференционных картин, возникающих при наложении отдельных пар волновых полей из всей совокупности интерферирующих волн. Принципы моделирования полихроматических интерференционных картин Выражение (8) описывает распределение интенсивности в плоскости регистрации или наблюдения интерференционной картины. Можно сказать, что функция IObbM (x, y) есть непрерывная функция двух непрерывных пространственных переменных x и y . Переменные x и y задают физические координаты в плоскости изображения, а функция lObjec (x, y) и есть само изображение. На практике чаще всего возможна работа не с непрерывным (иначе – аналоговым) изображением, а его цифровым представлением. Отличие цифрового изображения от аналогового заключается в его дискретной структуре. Координаты (x, y) , а следовательно, и сама функция IObbM (x, y) могут принимать не любые, а лишь строго определённые значения [21, 22]. В отношении координат (x, y) принято говорить о пространственной дискретизации изображения, а для функции /Object (x, y) определена операция квантования по уровням. Таким образом, вместо непрерывной функции lObjec (x, y) мы получаем в виде матрицы ограниченный набор значений интенсивности для конечной совокупности пар (x, y) . Однако при работе с цифровым изображением не имеет смысла говорить о физических координатах, а можно оперировать с элементами матрицы изображения и их индексами, принимая в расчёт период дискретизации исходного аналогового изображения. С этой точки зрения правильнее записывать функцию, характеризующую цифровое изображение, как IObbec' (nAx, mAy), где Ax и Ay - период дискретизации по соответствующим координатам, а n и m – индексы элементов матрицы изображения. Тем не менее, в дальнейшем, для простоты изложения, мы будем оперировать с переменными x и y , подразумевая их дискретный характер. Моделирование полихроматической интерференционной картины предусматривает необходимость расчёта и последующей визуализации цветного цифрового изображения. Для описания цвета цифровых изображений используется множество цветовых моделей или пространств [21, 22]. В качестве цветовой модели для расчёта и отображения полихроматической интерференционной картины в белом свете наиболее естественно взять модель RGB в силу того, что цветовое пространство RGB используется в цифровых устройствах регистрации изображений. Согласно этой модели цветное изображение какого-либо объекта состоит из трёх монохромных изображений – цветовых каналов, зарегистрированных при освещении объекта тремя монохроматическими источниками света – красным, зелёным и синим. Полученные в результате три матрицы содержат информацию о количестве того или иного цвета в каждой точке изображения. Цвет этой элементарной точки изображения или пикселя будет определяться соотношением между интенсивностью основных цветов. Смешение основных цветов в равных пропорциях даёт различные градации серого, от белого до чёрного. В действительности объект освещается одним источником белого света, а перед регистрирующей матрицей фотодетекторов расположены цветные светофильтры, при помощи которых и происходит выделение соответствующего спектрального диапазона из всего спектра падающего на матрицу фотодетекторов излучения. Таким образом, для расчёта полихроматической интерференционной картины необходимо рассчитать три числовые матрицы, каждая из которых соответствует изображению интерференционной картины, полученной при прохождении каждого из интерферирующих полей через цветной светофильтр, соответствующий тому или иному основному цвету цветового пространства. Следовательно, в подынтегральное выражение для каждого из интерферирующих полей, заданных уравнениями (7), должен входить множитель, описывающий спектр пропускания светофильтра. Тогда выражение (8) для интенсивности света в интерференционном изображении, получаемом в каждом из цветовых каналов, принимает следующий вид: МММ ^г ( x, y ) = r12 J fColor (to) g 2 (to) d®+ У J fColor (to) gB (to) dto+ r2 J /^ (to) g 2 (to) dto + М М +2Re ) ri r2 exp ( i (ф01 -ф02 )) J f^ (to) g 2 (to) exp i-(Ai ( x, y )-A2 ( x, y )) dto^ + I _ c _l М М +2Re ) ri rR exp ( i (фoi -фоR )) J f^,. (to) g 2 (to) exp i- (Ai ( x, y )-Ar ( x, y )) dto ^ + Inc I М +2Re ■ r2 rR exp ( i (ф02 -ф0R )) J fCoior (to) g2 (to) exp i to(AR ( x, y )- A2 ( x, y )) dto [, Inc I где fcotor (to) — амплитудный спектр пропускания соответствующего цветного фильтра. При моделировании интерференционных картин спектральные характеристики фильтров в шкале длин волн % представлялись в виде гауссовых контуров спектрального пропускания: fCOlOr (to) = exp Color где %о - центральная длина волны спектра про- пускания соответствующего фильтра, 2A%Color - ши- рина спектрального контура пропускания фильтра на уровне 1 e от максимального значения, а % = 2пс/и. Значения XColor и А%Color определялись из спецификации к камере DCU223C производства Thorlabs, ис- Рис. 3. Спектры пропускания цветных фильтров, установленных на матрице камеры (а), и спектры пропускания фильтров, использованные при моделировании и описываемые выражением (11) (б) Табл. 1. Спектральные характеристики фильтров, использованные при моделировании Фильтр Color %0 , нм А% Color , нм красный 610 39 зелёный 540 56 синий 460 58 Интерференционная картина за пределами неод- нородности определяется выражением: l a ( x, y ) = ^ ^ = Гз2 J g2 (®) d®+ rR J g2 (®) d®+ 00 +2Re (rRr3exp (i (фю -ф0r ))x ™ г , пользовавшейся в экспериментальной системе. Спектры пропускания цветных фильтров камеры представлены на рис. 3, а соответствующие значения XColor и А% Color для каждого из фильтров приведены в таблице 1. xJ g2 (® exp i ®(AR (x, У)) d® r0 L c J J для которого распределение интенсивности дом из цветовых каналов б удет иметь вид: ^ Clear 2 2 2 IColor (x, У ) = r3 J fColor (®) g (®) d® + ^ +r2 J fColor (®) g2 (®) d® + +2Re{ rRr3exP ( i (ф03 -ф0 R ))x ™ в каж- ^ XJ f^r (®) g2 (®) exp i-(A R ( x, У )) d® [ . _ c _l Результаты моделирования полихроматических интерференционных картин С использованием уравнений (10) и (13) рассчитывались распределения интенсивности в интерференционном изображении для каждого из трёх цветовых каналов, после чего формировалось результирующее цветное изображение, представляющее собой интерференционную картину в белом свете. Этот процесс последовательно представлен на рис. 4. В качестве функции, описывающей форму поверхности неоднородности, было взято уравнение параболоида вращения: z (x, У ) = z011I, (14) I r) где z0 – максимальная высота неоднородности в точке x = 0, y = 0 , r - радиус неоднородности. Различие в характере зависимости разности хода от координат (x, y) для волны, отражённой от верхней поверхности неоднородности, и волны, отражённой от поверхности подложки под неоднородностью, приводит к изменению направления искривления интерференционных полос при наложении опорной волны, что ясно иллюстрируется рис. 5б и 5в. Выражения (10) и (13) позволяют рассчитать полихроматическую интерференционную картину от исслед уемого объекта как при наличии опорной волны, так и при отсутствии её. Для этого достаточно приравнять нулю коэффициент отражения опорного зеркала rR , оставив при этом н еизменными параметры, отвечающие за геометрию неоднородности – z0 и r , и за её физически е свойства – показатель преломления n . Полученная в результате интерференционная картина (рис. 5а) демонстрирует наличие интерференционных полос при отсутствии опорной волны, являющихся результатом интерференции двух волн, отражённых от верхней и от нижней поверхности неоднородности. Наблюдаемая результирующая интерференционная картина с опорным пучком представляет собой наложение трёх интерференционных картин, приведённых в отдельности на рис. 5. Для расчёта были взяты след ующие параметры: высота неоднородности z0= 500 нм, радиус неоднородности r = 4 мкм, показатель преломления n = 1,6, значения ампли- тудных коэффициентов отражения - r1 = 0,05, r2 = 0,5, r3 = 0,5, rR = 0,8. б) Рис. 4. Формирование цветного изображения интерференционной картины: RGB-компоненты изображения (а)-(в) и результирующее цветное изображение (г) Рис. 5. Составляющие полихроматической интерференционной картины, изображенной на рис. 4г: результат интерференции волн, отражённых от границ неоднородности без участия опорной волны (а); результат интерференции волны, отражённой от верхней границы неоднородности, и опорной волны (б); результат интерференции волны, отражённой от нижней границы неоднородности, и опорной волны (в) В работах [10-11] реализована схема так называемой полнопольной интерференционной микроскопии со сканированием разности хода волн в предметном плече. В модельном численном эксперименте аналогичный механизм сканирования может быть реализован путём изменения разности хода в опорном плече 2AzR (z) в уравнениях (10) и (13). Строго говоря, эти два способа перестройки оптической разности хода в реальном интерферометре не идентичны. При перемещении объекта вдоль оптической оси или при перемещении интерферометра относительно объекта к влиянию на интерференционную картину когерентных свойств полей добавляются эффекты дефокусировки изображения объекта. Однако сказанное справедливо для высокоапертурных систем, при использовании микрообъективов с числовой апертурой NA > 0,65 [23]. В нашем конкретном случае использования системы на базе микроинтерферометра Линника со штатным микрообъективом с числовой апертурой NA = 0,65 указанными эффектами можно пренебречь. В процессе сканирования из трёх составляющих общего изображения, представленных на рис. 5, изменениям будут подвергаться лишь те, в формирова- нии которых участвует опорная волна. Это интерферограммы на рис. 5б и 5в . Изображение, представляющее собой результат взаимной интерференции волн, отражённых двумя границами неоднородности (рис. 5а), будет оставаться постоянным, формируя тем самым дополнительную постоянную составляющую в области локализации неоднородности. При подобном сканировании, посредством перемещения опорного зеркала, или изменения 2AzR (z), при одновременной записи интерферограмм в плоскости (x, y), или их расчёте с использованием уравнений (10) и (13), формируется трехмёрная интерферограмма, сечение которой плоскостью (x, z) изображено на рис. 6а. 2kzR(z), мкм б) Рис. 6. Интерферограмма объекта в плоскости (x,z ), полученная путём сканирования оптической разности хода в опорном плече при изменении 2 Az R ( z ) На этой интерферограмме каждая строка соответствует своему значению 2AzR (z), а сама интерферограмма представ ляет собой сечение оптической структуры исследуемого объекта плоскостью (x, z) , аналогично томографическим срезам, получаемым при сканировании объекта в интерференционном микроскопе. Так как расчёт исходных интерферограмм в плоскости (x, y) выполнялся в цветовом пространстве RGB, то каждая строка рис. 6а представлена в виде суммы цветовых каналов, иначе говоря, характеризует яркостную составляющую цветного изображения. Для примера на рис. 6б приведено сечение интерферограммы вертикальной линией, обозначенной на рис. 6а, отдельно по каждому цветовому каналу и по сумме цв етовых каналов. Экспериментальная полихроматическая интерферометрия эритроцитов крови Для интерферограмм на рис. 4-6 в качестве примера для описания формы поверхности неоднородности было использовано уравнение параболоида. Вместо него можно использовать любое выражение, удовлетворительно описывающее поверхность реального объекта, исслед уемого в интерференционном эксперименте. Метод интерференционной микроскопии широко используется для исследования биологических объектов, в частности, отдельных клеток, которые, в определённом смысле, могут рассматриваться как прозрачные, слоистые объекты или тонкие плёнки. Такими объектами могут служить эритроциты в тонком мазке крови. На рис. 7 приведено микроскопическое изображение фрагмента мазка крови с содержащимися в нём одиночными эритроцитами на различных подложках с высокоот-ражающей (рис. 7а-е) и стеклянной (рис. 7ж-л) поверхностями при отсутствии (рис. 7а, в, д, ж, и, л) и при наложении (рис. 7б, з, г, е, к, м) опорной волны. д) е) л) м) Рис. 7. Микроскопические интерференционные изображения фрагмента мазка крови на высокоотражающей (а)-(е) и стеклянной (ж)-(м) поверхностях При использовании подложки с высокоотра-жающей поверхностью формируются в отсутствие опорного пучка интерференционные изображения с более высоким контрастом интерференционных полос и более высоким цветовым контрастом ин- терференционного изображения, чем при использовании стеклянной поверхности. Это обусловлено достаточно большой интенсивностью световой волны, отражённой от нижней поверхности эритроцита, совпадающей с поверхностью подложки. Уравнением, достаточно точно описывающим двояковогнутую форму эритроцита, служит уравнение поверхности, полученной в результате вращения двумерной фигуры, известной как овалы Кассини [24], пример которой приведён на рис. 8а, а на рис. 8б представлен пример трёхмерной поверхности. Рис. 8. Овалы Кассини на двумерной плоскости (а) и трёхмерная поверхность (б), образованная вращением Уравнение поверхности, образованной вращением овалов Кассини, может быть задано в виде: z (X, y) = = ±^aa2(x2+ y2) + c4- a2- x2- y2, где знак «–» соответствует участку поверхности, лежащ ему в области отрицательных значений z , поэтому, чтобы получить форму поверхности, изображённую на рис. 8б, достаточно взять положительную часть уравнения (15). Смысл параметра a ясен из рис. 8а, а параметр c2 определяет произведение расстояний от любой точки поверхности до точек F1 и F2 . Чтобы получить форму поверхности аналогичную изображённой на рис. 8, параметры a и c должны удовлетворять неравенству a < c < a-\T2 . Следует заметить, что форма поверхности, описываемая выражением (15), является лишь одной из известных форм эритроцитов, характерной для здоровой клетки в свободном потоке. Для эритроцита в сухом мазке крови данная модель неприменима, однако она достаточно хорошо описывает поведение во времени осаждённого на поверхность эритроцита в только что нанесённом мазке крови, что подтверждается наблюдением изменения интерференционной окраски изображений эритроцитов на высокоотражающей подложке (рис. 7д-е). В течение 10-15 минут после нанесения его форма изменяется и принимает уплощённый вид (7а-г, 7ж-м). После этого основную долю поверх- ности клетки можно рассматривать как тонкую плёнку с незначительной вариацией толщины. На рис. 9 представлены полихроматические интерферограммы, рассчитанные для формы неоднородности, заданной положительной частью формулы (15) и изображённой на рис. 8б. По аналогии со случаем параболоида на рисунке приведены интер- ферограммы, полученные как с участием опорной волны, так и без неё при интерференции волн, отражённых верхней и нижней границами неоднородности. На рис. 10 представлен в градациях серого двумерный поперечный скан по глубине объекта и одномерный скан вдоль выделенной линии, обозначенной на рис. 10а. Рис. 9. Составляющие полихроматической интерференционной картины (а)-(в), интерференционная картина от неоднородности, форма поверхности которой задана уравнением (15) (г) 2AzK(z), мкм ^ присный б) Рис. 10. Интерферограмма объекта в плоскости (x,z ), полученная путём сканирования оптической разности хода в опорном плече при изменении 2AzR (z) Обсуждение и заключение В большинстве практических случаев регистрируемое изображен ие интерференционной картины имеет сложную структуру, расшифровка которой треб ует знания априорной информации. К примеру, анализ интерферограмм на рис. 4 и 9 показывает, что в структуре объекта присутствуют две отражающие границы разного знака кривизны поверхности. При этом возникает неопределённость при интерпретации интерферограммы – какая система полос соответствует той или иной отражающей поверхности. В идеализированных случаях, приведённых на рис. 4 и 9, система невозмущённых интерференционных полос за пределами неоднородности и априорное знание коэффициентов отражения каждой из границ плёнки позволяет сделать однозначный вывод о том, что менее контрастная систем а полос возникает в результате интерференции опорной волны с волной, отражённой от верхней поверхности плёнки, тогда как более контрастная система полос является результатом интерференци и опорной волны с волной, отражённой от нижней границы плёнки. При сравнении интерферограмм реальных объектов на рис. 7 и рассчитанных теоретически интерференционных картин на рис. 4в и 9г можно выявить ряд общих черт в картине распределения ин-терферен ционных цветов по поверхности исследуемого объекта, положения и характера ис кривления центральной полосы, контраста интерференционных полос. Достаточно простая геометрическая модель поверхности объекта, записанная в виде уравнения (14) или (15), позволяет достичь удовлетворительной степени соответствия экспериментальных и теоретических интерферограмм. В этом можно убедиться, сравнив попарно рис. 7з и 4г, 7е и 9г. В настоящей работе используется спектральное представление интерферирующих полей и самого интерференционного уравнения. Такой подход, в отличие от непосредственного задания функции когерентности, позволяет учитывать при анализе интерферограмм спектральные свойства как самого объекта, так и интерференционной системы, при помощи которой он исслед уется. Как правило, говоря о разрешающей способности интерференционных методов визуализации структуры объектов, подразумевают длину временной когерентности осве- щающего объект излучения. При этом чаще всего не учитываются кривые спектральной чувствительности регистрирующих элементов, или спектры пропускания светофильтров. В то время как именно спектральные свойства регистрирующ ей аппаратуры оказывают доминирующее влияние на когерентные свойства оптических полей, так как спектр излучения большинства тепловых источников света значительно шире кривой спектральной чувствительности детекторов излучения. При моделировании интерферограмм на рис. 4 и 9 амплитудный спектр излучения источника g (to), как и спектр цветных светофильтров, представлялся в виде гауссова контура (11), где X0ource = 535 нм, а AX source = 500 нм, изображённого на рис. 11 пунктирной линией. Рис. 11. Спектры излучения лампы накаливания (1), модельного источника (2) и эффективный спектр источника (3) при регистрации с использованием RGB-матрицы Штриховой линией обозначен спектр излучения лампы накаливания, использованной в интерференционном микроскопе. Оба этих графика показывают, что эффективная ширина спектра интерферирующих полей б удет определяться спектром пропускания цветных светофильтров (рис. 3), установленных перед светоч увствительными элементами цифровой камеры. Рис. 6б наглядно показывает различие межд у импульсами когерентности, зарегистрированными в различных цветовых каналах цифровой матрицы. Очевидно, что ширина импульса когерентности будет определяться шириной спектрального контура пропускания соответствующего светофильтра (рис. 3, табл. 1). Полуширина импульса когерентности, определяемого совокупным влиянием спектров пропускания всех трёх фильтров и получаемого как яркостная компонента RGB-изображения (рис. 6б), для параметров, использованных при моделировании в рамках настоящей работы, на уровне 1 e от максимального составила = 0,6 мкм. Несложно рассчитать, воспользовавшись соотношением Винера-Хинчина, что результирующая функция когерентности соответствует спектральной кривой, изображённой на рис. 11 сплош- ной линией , ширина которой на уровне 1 e составляет = 220 нм, что значительно меньше ширины спектра излучения источника, использованного при моделировании. Спектр излучения, изображённы й на рис. 11 сплошной линией, может быть расценен как эквивалентный (или эффективный) спектр излучения источника. Изложенные выше суждения и расчёты показывают необходимость использования соответствующих теоретических представлений и математического аппарата для ан ализа и интерпретации полихроматических интерферограмм с целью учёта особенностей цифровых устройств регистрации изображений. В ст атье представлен теоретический подход, учитывающий такие особенности метода интерференционной микроскопии, как наложение нескольких интерференционных картин, возникновение интерференционных картин как при наложении опорной волны, так и в тонком слое или плёнке внутри объекта, изменение спектрального состава интерферирующих полей, а следовательно, и когерентных свойств этих полей при прохождении их через светофильтры цветных цифровых камер. Являясь более общим, нежели частное решение через функцию временной когерентности (выражения (2) и (5)), такой подход представляется более гибким инструментом, позволяющим эффективно решать прямую задачу моделирования интерференционных картин, наблюдаемых в интерференционном микроскопе. Уравнения (10) и (13), полученные для частного случая тонкой плёнки с двумя отражающими границами, расположенной на подложке, легко масштабируются до любого количества слоёв и отражающих границ. Результирующая интерферограмма в общем случае б удет представлять собой результат некогерентного сложения элементарных интерференционных картин от двух волн, отражённы х парами границ слоистого объекта. Особенности регистрации цветны х интерференционных картин в цифровых системах требуют тщательного исследования, поскольку даже предварительные результаты, изложенные в данной работе, указывают на существенное влияние на когерентны е свойства оптических полей спектральных свойств регистрирующей аппаратуры. В настоящей статье изложены теоретические основы для подобного рода исследований и приведён пример их практического применения. Исследования проведены в рамках выполнения аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы (2009-2010 годы)» и государственного контракта № 02.740.11.0879. Авторы выражают свою благодарность за плодотворное обсуждение и помощь в подготовке экспериментального материала Д.В. Лякину, О.А. Перепелицыной, Л.И. Малиновой и А.А. Пайзиев у.