Non-linear filtering of chaotic signal in the presence of noise
Автор: Kazimirov A.N., Telezhkin V.F.
Рубрика: Краткие сообщения
Статья в выпуске: 3 т.18, 2018 года.
Бесплатный доступ
The creation of radio engineering systems based on the effects of stochastic and chaotic dynamic is a promising direction. The task of developing such systems must be oriented toward using the results of theoretical studies of processes in nonlinear radiophysical systems. The subject of this study is the nonlinear filtering of a mixture of chaotic oscillations and noise based on the stochastic resonance effect occurring in a bistable system with the aim of isolating the information chaotic signal. Usually, noise is considered to be “white”, and the signal is narrow-banded. As a bistable system, a Schmitt trigger can be used. For narrowband signals, the stochastic resonance effect has been studied in sufficient detail theoretically, for broadband information signals, applied research is insufficient. The stochastic resonance effect is a phenomenon in which the response of a nonlinear system to a weak external signal amplifies with increasing noise intensity to some optimal value. In the study of radio engineering systems, chaotic oscillations can be used as information systems. Theoretical basis for research of information processing systems in radio engineering systems using chaotic signals is research in the field of nonlinear radiophysics. Of particular importance in this case is the selection of solutions at the model level, in particular, based on the results of circuit simulation of practically realized devices on the existing element base.
Stochastic resonance, chaotic dynamics, bistable system, schmitt trigger, nonlineardynamical system, optimal noise level, nonlinear filter, spectral analysis of the investigated oscillations
Короткий адрес: https://sciup.org/147232194
IDR: 147232194 | УДК: 612.17 | DOI: 10.14529/ctcr180314
Текст краткого сообщения Non-linear filtering of chaotic signal in the presence of noise
-
1. Introduction
-
2. Modelling
Development of radio technical systems based on the effects of stochastic and chaotic speaker is promising. The task of developing such systems it is necessary to focus on using the results of theoretical research of processes in nonlinear radiophysical systems. To describe the dynamics of such systems are used nonlinear differential equations of Lorenz or Ressler model type [1, 2] are mainly used to describe the dynamics of such systems. Currently, to generate chaotic signals are used by models on the basis of the generator Chua [3, 4], logistic map, TENT-dimensional display and two dimensional display of Hannon [5–9], three or more high-dimensional mappings display Richter [10–14], the generator of the Van der Pol nonlinear feedback [15].
The subject of this research is the nonlinear filtering of a mixture of chaotic oscillations and noise on the basis of the effect of stochastic resonance occurring in a bistable system, with the objective of allocating the information of a chaotic signal. Usually believe the noise is “white”, and the signal is narrowband. As a bistable system can be applied Schmitt trigger. In this formulation, the effect of stochastic resonance is investigated completely enough in theory. The effect of stochastic resonance is a phenomenon in which the response of a nonlinear system to a weak external signal increases with the increase of the noise intensity up to a certain optimum value. The real-time information signals have a certain frequency band, taking into account current trends on the use of complex modulation schemes and the extension band signals to transmit information, it is necessary to consider the phenomenon of stochastic resonance in application to such signals. When you use the phenomenon of stochastic resonance in a bistable nonlinear dynamical system, the conditions for enhancing weak information signal as a result of its interaction with noise. For the simulation of a real information signal (speech, music) can be used of the chaotic oscillation. Chaos, presented in the form of time sequence data is viewed as a manifestation of a deterministic dynamics, albeit complex, typical for nonlinear systems. From a modern point of view of chaotic and stochastic oscillations can be identified by various methods. Nonlinear dy- namic systems exhibiting chaotic dynamics, and under the influence of noise is studied in theoretical terms. There are applied research in nonlinear filtering, but they are dedicated to the signals with the classical modes. To bring the theoretical research at the level of mathematical models for practical use in radio engineering systems, for example, the effect of stochastic resonance for signal extraction from additive mixture of signal and noise is a challenge for further research. In most of the studies have noted the potential use of the effect of stochastic resonance to enhance the relationship of signal power to noise power. Are invited to explore these processes in the applied aspect, the program circuit simulation Multisim. Previously, the results of mathematical modeling were presented at the previous conference [16].
In Multisim assembled generator of chaotic oscillations of nonlinear filter based on the bistable system, the Schmitt trigger, the noise source is an internal generator “thermal_noise”. What is happening, in such a system, processes are observed and analyzed using the virtual instruments. In Fig. 1 a model diagram of the entire device is shown. Generation of chaotic oscillations is a transistor oscillator with a resonant system, ladder type. Schmitt trigger and other auxiliary devices are assembled on operational amplifiers.
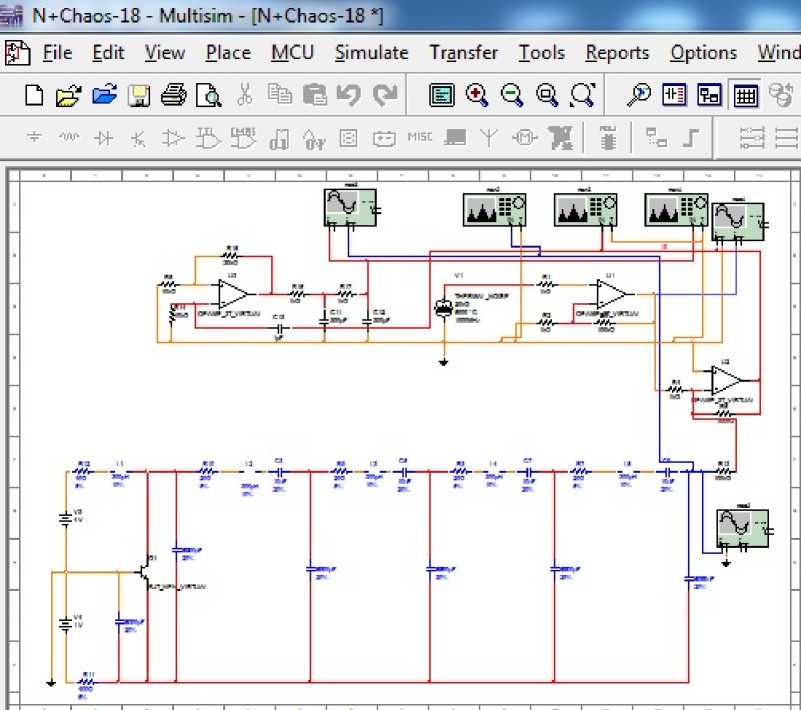
Fig. 1
In Fig. 2 an example of the entire device is shown, the processes are displayed on the monitors virtual devices. Top left are the waveforms of the input and output passed through the nonlinear filter of fluctuations. Below, respectively, the implementation of noise and signal with added noise. Right, top to bottom, respectively, the spectrum of the signal with added noise, the spectrum of the signal and the spectrum of fluctuations at the output of the nonlinear filter. The parameters of all three spectrum analyzers are the same [17].
In the absence of noise the signal level is insufficient to switch the Schmitt trigger, so the output signal of the nonlinear filter (Fig. 3).
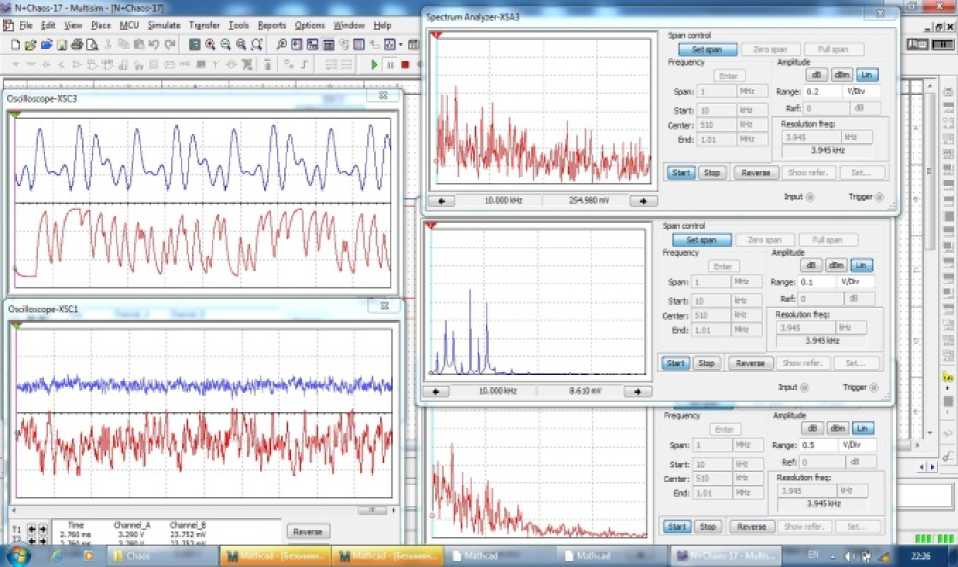
Fig. 2
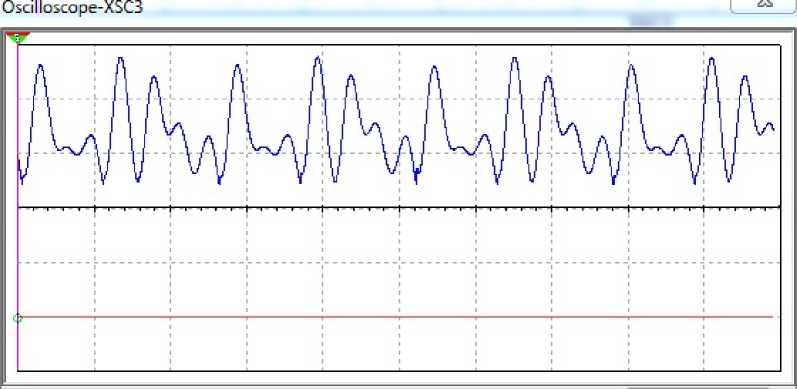
Fig. 3
The spectrum of chaotic oscillations (envelope spectrum) at the output of the transistor oscillator is shown in Fig. 4.
In Fig. 5 the spectrum of the noise added to the chaotic oscillation is shown.
A mixture of chaotic oscillations and noise, and separate the “noise path” is shown in Fig. 6.
Switching of the Schmitt trigger begins to happen, but the noise level is still far from optimal and the dynamics of the process at the output of the nonlinear filter does not match the signal, chaotic oscillation at the input (Fig. 7).
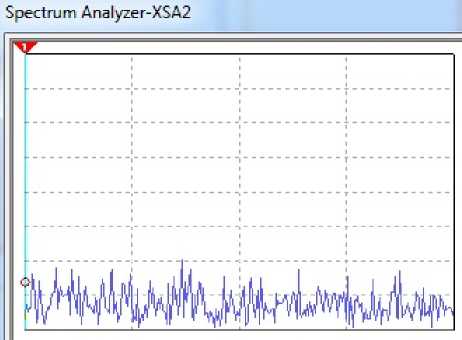
Fig. 5
Spectrum Analyzer-XSA2
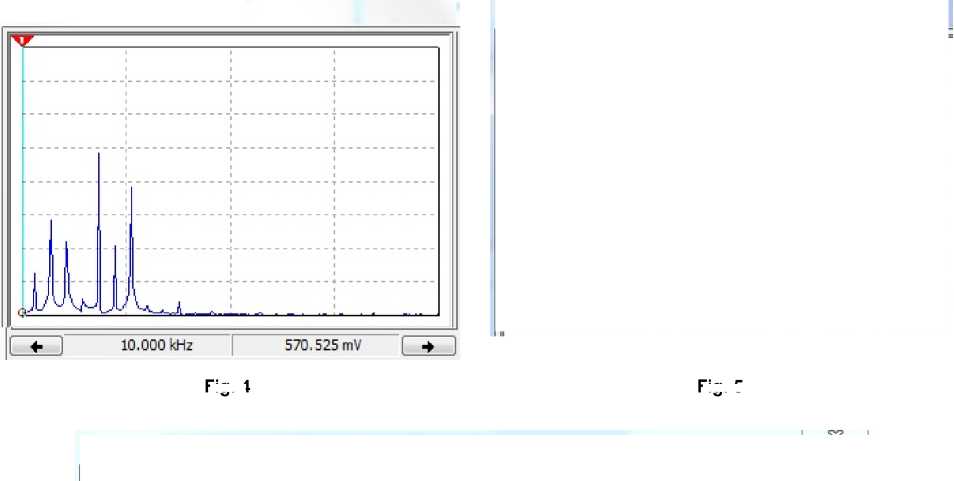
Fig. 4
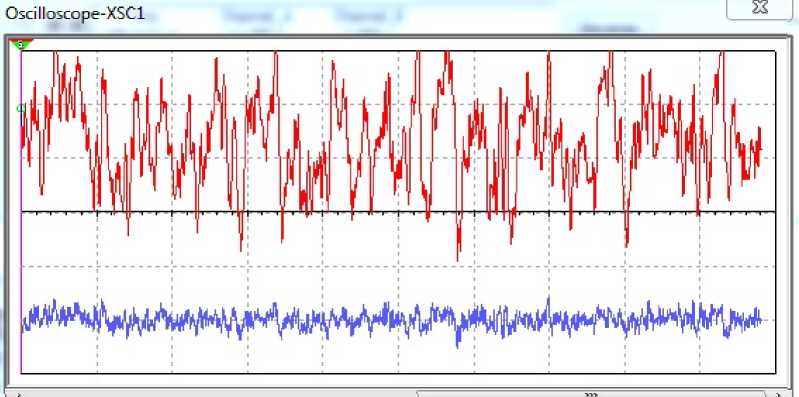

Fig. 6
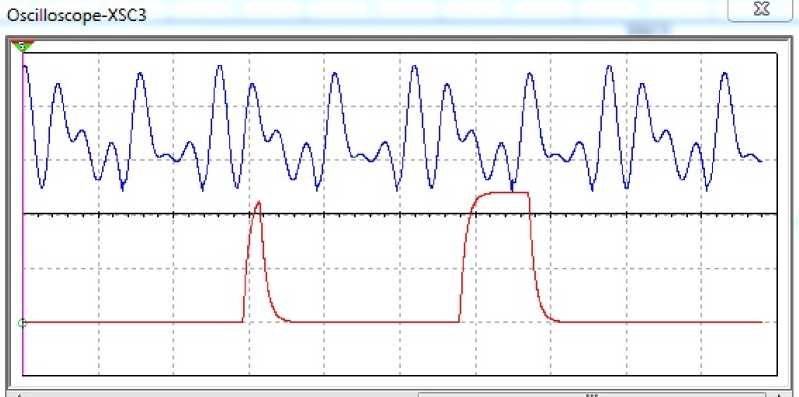
Fig. 7
If the noise level increases and becomes close to the optimum, then input signal and its spectrum appear quite noisy (Fig. 8 and 9).
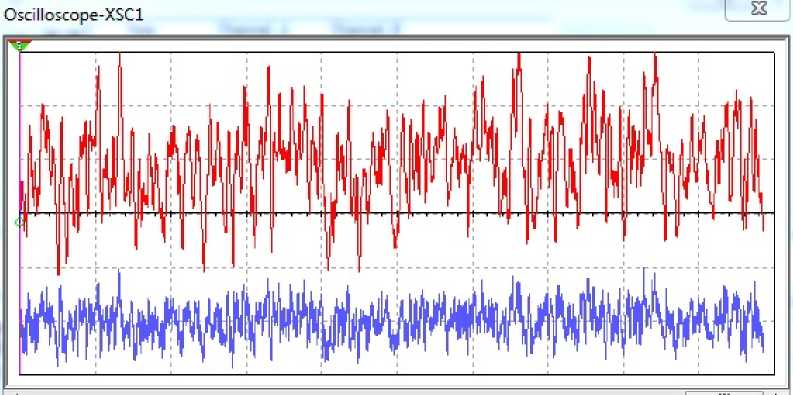
Fig. 8
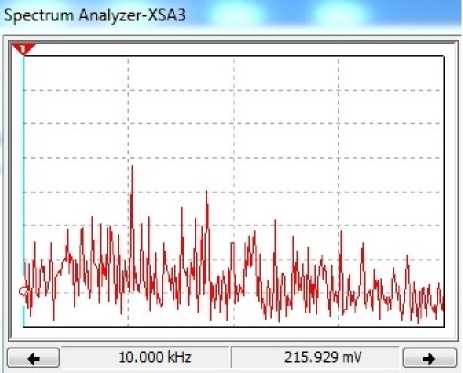
Fig. 9
The input oscillation and the oscillation output of the Schmitt trigger for this case is shown in Fig. 10.
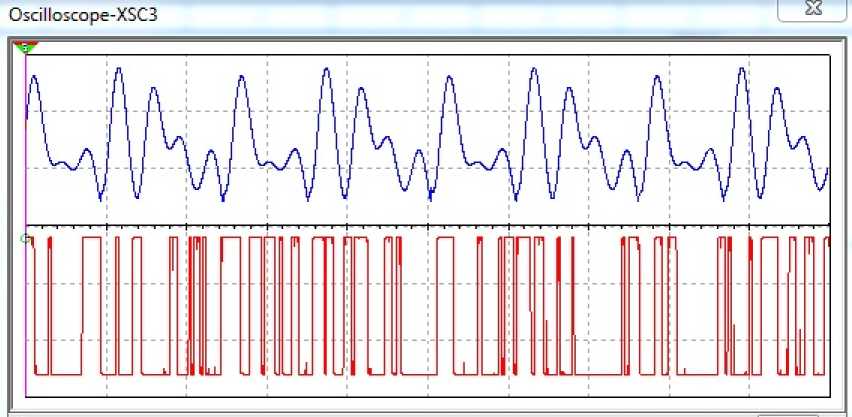
Fig. 10
In the case of optimal noise spectrum of the input fluctuations (additive mixture of chaotic oscillations and noise) is shown in Fig. 11, and the chaotic oscillation and the oscillation at the output of the nonlinear filter – in Fig. 12. The spectrum of output fluctuations, respectively, is in Fig. 13.
Spectrum Analyzer-XSAl
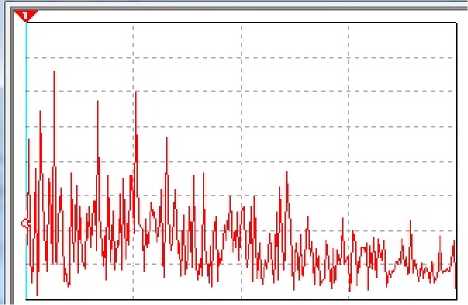
Fig. 11
Osci I Iosco pe-XSC3
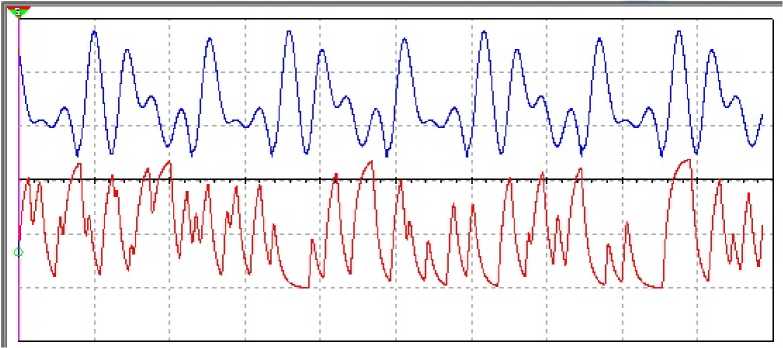
Fig. 12
Spectrum Analyzer-XSAl
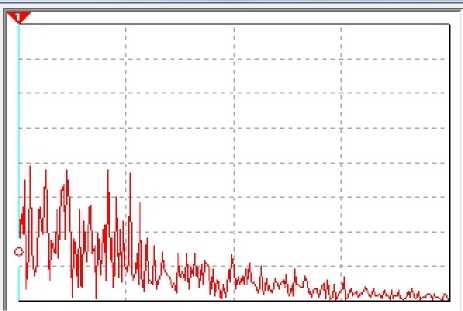
Fig. 13
With increasing noise levels above the optimum in Fig. 14 shows the original chaotic oscillation and the oscillation at the output of the nonlinear filter. The spectrum of output oscillations is in Fig. 15.
In the spectrum of the output oscillations increases the level of high frequency components and the whole dynamics of the output process less corresponds to the original chaotic oscillation.
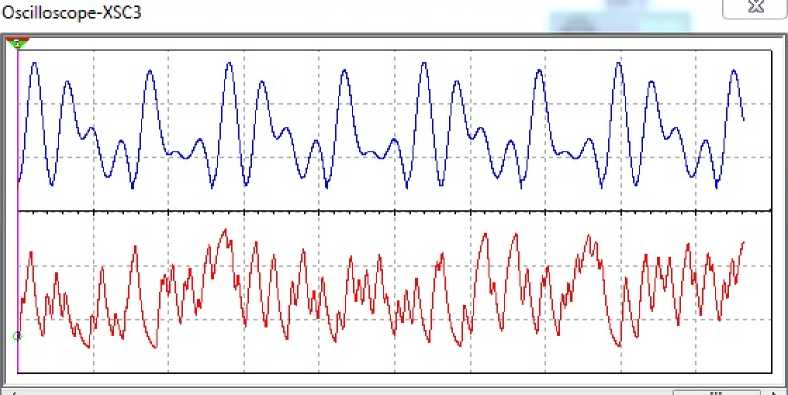
Fig. 14
Spectrum Analyzer-XSA2
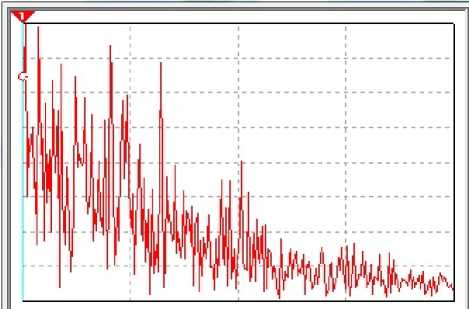
Fig. 15
Studies have shown the possibility of separating complex signal from its mixture with noise. Circuit simulation reduces the time of study compared to the theoretical research and then will quickly move to the physical implementation of the device.
Список литературы Non-linear filtering of chaotic signal in the presence of noise
- Lorenz, E.N. Deterministic Nonperiodic flow / E.N. Lorenz // J. Atmos. Sci. - 1963. - Vol. 20. - Р. 130-133.
- Rossler, O.E. An Equation for Continuous Chaos / O.E. Rossler // Phys. Lett. A. - 1976. - Vol. 57A, 5. - Р. 397-398.
- Matsumoto, T. A Chaotic Attractor from Chua's Circuit / T. Matsumoto // IEEE Trans. Circuits Syst.. - 1984. - Vol. CAS-31. - Р. 1055-1058.
- Zlong, G.-Q., Ayrom F. Experimental Confirmation of Chaos from Chua's Circuit / G.-Q. Zlong, F. Ayrom // Int. J. Circuit Theory Appl. - 1985. - Vol. 13. - Р. 93-98.
- "Crossroad Area - Spring Area" Transition (I) Parameter Plane Representation / J. Carcasses, C. Mira, M. Bosch et al. // International Journal of Bifurcation and Chaos. - 1991. - Vol. 1, no. 1. - Р. 183-196.
- "Crossroad Area - Spring Area" Transition (II). Foliated Parametric Representation / J. Carcasses, C. Mira, M. Bosch et al. // International Journal of Bifurcation and Chaos. - 1991. - Vol. 1, no. 2. - Р. 339-348.
- Elhadj, Z. A Minimal 2-Dquadratic Map with Quasi-periodic Route to Chaos / Z. Elhadj, J.C. Sprott // International Journal of Bifurcation and Chaos. - 2008. - No. 5. - Р. 1567-1577.
- DOI: 10.1142/S021812740802118X
- Froeschlé, С. Analysis of the Chaotic Behaviour of Orbits Diffusing along the Arnold Web / С. Froeschlé, E. Lega, M. Guzzo // Celestial Mechanics and Dynamical Astronomy. - 2006. - Vol. 95, iss. 1-4. - Р. 141-153.
- DOI: 10.1007/s10569-006-9004-2
- Guzzo, M. First Numerical Evidence of Global Arnold Diffusion in Quasi-Integrable Systems / M. Guzzo, E. Lega, С. Froeschlé // Discrete and Continuous DynamicalSystems - Series B. - 2005. - Vol. 5, no. 3. - Р. 687-698.
- DOI: 10.3934/dcdsb.2005.5.687
- Richter, H. The Generalized Henon Maps: Examples for Higher-Dimensional Chaos / H. Richter // International Journal of Bifurcation and Chaos. - 2002. - Vol. 12, no. 6. - Р. 1371-1384.
- DOI: 10.1142/s0218127402005121
- Richter, H. On a Family of Maps with Multiple Chaotic Attractors / H. Richter // Chaos, Solitons & Fractals. - 2008. - Vol. 36, no. 3, Р. 559-571.
- DOI: 10.1016/j.chaos.2007.07.089
- Classification of Three-Dimensional Quadratic Diffeomorphisms with Constant Jacobian / Z. Elhadj, J.C. Sprott // Frontiers of Physics in China. - 2009. - Vol. 4, no. 1. - Р. 111-121.
- DOI: 10.1007/s11467-009-0005-y
- Kaneko, K. Doubling of Torus / K. Kaneko // Progress of Theoretical Physics. - 1983. - Vol. 69, no. 6. - Р. 1806-1810.
- DOI: 10.1143/ptp.69.1806
- Stagliano, J. Doubling Bifurcations of Destroyed T2 Tori / J. Stagliano, Jr. Wersingera, E. Slaminkab // Physica D. - 1996. - Vol. 92, no. 3-4. - Р. 164-177.
- DOI: 10.1016/0167-2789(95)00273-1
- Beck, C. Thermodynamics of Chaotic Systems / C. Beck, F. Schlogl. - Cambridge: Cambridge Univ. Press, 1993. - 461 p.
- Казимиров, А.Н. Генератор сверхширокополосного фрактального сигнала для радиотехнических систем связи / А.Н. Казимиров, В.Ф. Тележкин // Доклады 16-й Международной конференции «Цифровая обработка сигналов и их применение» (DSPA-2014). - М., 2013. - Т. 1. - С. 401-404.
- Домбровский, А.Н. Стохастический резонанс и фильтрация сигналов в нелинейной системе второго порядка / А.Н. Домбровский, С.А. Решетняк // Радиотехника. - 2007. - № 9. - С. 19-25.


