Non-linear model of the damping process in a system with a two-mass pendulum absorber

Published Online January 2019 in MECS

In the previous article of the authors [1], a mathematical model of the process of suppression of forced vibrations of a vibration protection system using a two-mass pendulum absorber was constructed. The mathematical model was presented in the form of two nonlinear equations, which were linearized for the subsequent numerical investigation in a linear formulation. The numerical analysis of dynamic effects in a linear system has shown [1] that the level of dynamic effects on the carrier bodies can be significantly reduced in the region of resonance frequencies. However, the optimum tuning of the absorber's parameters is possible only in the presence of the amplitude-frequency characteristic (AFC) of the system under investigation in a nonlinear setting. Its absence restrains the introduction of the proposed absorbers into the practice of vibration protection of load-bearing objects. Thus, the determination of the frequency response of the system under consideration in a nonlinear formulation and its use for tuning the absorber is an actual theoretical and practical task.

• II.    Formulation of the Problem

The forced vibrations of a damping system of coupled solids "a carrier body - a two-mass pendulum absorber" under the influence of external harmonic action are considered. Fig. 1 shows a general view of the vibration protection system under consideration. The description of all components of the system and their technical purpose are given in the previous article of the authors [1], we do not mention them here. In the meanwhile, the advantages of the proposed pendulum absorbers in front of the traditional damping devices were noted. In this article, the study will be conducted without imposing restrictions on the angles of the deviation of the axis of the pendulum from the vertical. The purpose of the work is therefore formulated below.

The aim of this work is to analyze construction of the equations of the frequency response of the vibration protection system and to determine of the optimal tuning parameters for a two-mass pendulum absorber in a nonlinear setting .

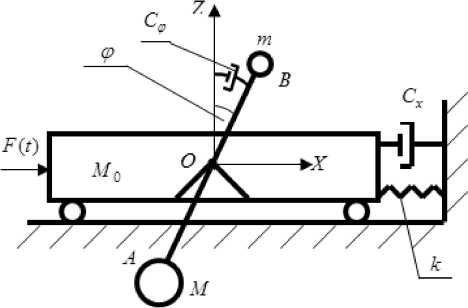
Fig.1. Damping system with a two-mass pendulum absorber under the influence of external harmonic excitation F(t)

• III.    Constrution of the Equations of Frequency Response in Nonlinear Formulation

In [1], nonlinear differential equations of motion of the system were obtained in this form:

(1 + V + д ) Х 0 + 2 n x x 0 + 6 0 x₀ +

+ p ( ф ²sin ^ - ^ cos ^ ) = F ₀ sin( m t )         (1)

x ₀cos 3 = qф + 2 п_фф + g sin ф ,          (2)

where v = M/M ₀ ; д = m/M ₀ ; F₀ = F ₀ / M ₀ ; 6 2 = kM ₀ ; 2 n_x = CjM ₀ ; A = ML - ml ; p = A/ M ₀ ; S = MI? + ml ²; q = ^A ; 2 п_ф = С_ф /A.

The structure of these equations completely corresponds to the structure of the equations obtained in the fundamental monographs [2, 3], in which one of the authors explored in detail the kinematics and dynamics of the roller absorbers of forced oscillations. Therefore, we use the approach developed in this study [3].

We expand the trigonometric functions in the Taylor series and keep two terms of the corresponding series for each function. After this, the obtained two-term segments of the series into equations (1) – (2) is substituted. As a result, it turns out:

use the Ritz averaging method [4 – 6]. This method is based on the assumption that the average value of the virtual work, which is performed during the motion of all the elements of the system in one period, the final outcome is zero.

When using the Ritz averaging method, it is believed that an approximate solution of forced oscillations of a mechanical system for each independent coordinate X j ( t ) can be represented as a finite series:

n

^X j ( t ) = £ A j vi( t ) ,               ⁽⁵⁾

i I where ^i - are some basic time functions that are selected from the condition of the problem and the specifics of the system; Aij - weight coefficients, which are determined from the condition that the average value of virtual work for one period of oscillations is zero.

Usually, for an approximate steady-state solution, the problems are limited to one or two terms of the series (5). In this paper, for each independent generalized coordinate, the following functions are suggested:

x₀(t ) = A ^ 1 ( t ) + A ₂ ^ ₂ ( t ) = A sin( 6 t - a ) ,     (6)

3 ( t ) = B ^ 1 ( t ) + B 2 V 2 ( t ) = B sin( 6 t - в ),     (7)

where ^ 1 ( t ) = sin ( to t ) и ^ ₂ ( t ) = cos ( to t ) .

After substituting expressions (6) and (7) into equations (3) and (4), a system of nonlinear algebraic equation is obtained:

2 n_xA to cos( to t - a ) - (1 + v + д ) б²A sin( 6 t - a ) +

+ A to 2 sin( 6 t - a ) +

+ pB ³ 6²

.   B ² . _2/ ,                   _ 2z ,       ,

1--sin²( 6 t - в ) sin( 6 t - e )cos²( 6 t - в ) +

21 B ²    ₂         1              -

+ pB to² 1 - — sin² ( to t - в ) sin( 6 t - в ) = F ₀ sin( 6 t ),

2           ^ф

⁽¹ + ^V + Д ) ^x 0 + ² n x x ₀ + 6 2 ^x 0 ⁺ p V- —

3 2

—

—

(   3 ²1               .

■ p 1 - — ф = F ₀sin ( ro t ) ,

. 2.,. x l b ²._2/. „а

A ro sin( to t - a ) 1--sin ( m t - в ) =

I ²              J

= qBm² sin( m t - в ) - 2 n ₃ B m cos( m t - в ) -

—

„I,     B ² . 2/        ,, I • ,

• gB 1--sin²( ® t - в ) sin( ® t - в ).

^x 0 ¹ -^ = Ч Ф ^{+ 2 п} ф Ф ⁺ g 3

з A

_ 3

,

The paper considers steady-state oscillations of the system. When constructing the equations of the frequency response of the damping system under consideration, we

To transform equations (8) and (9) in the following way, it multiplies these equations first by sin( m t ) and integrate them on the interval from 0 to 2 n . Then it carries out the same integration after multiplying these equations by cos( m t ) . After the corresponding

transformations, four algebraic equations are obtained:

sin( a — в ) =

( to 0 — (1 + v + ^ ) to ²) A cos a + 2 n x A to sin a +

pB to cos в 1

B ²

B 4 1

—

= F o^.

2 n x A to cos a — ( to 0 — (1 + v + ^ ) to ²) A sin a —

2 n ^ B

4 fl B ²1

A to 1

I ⁸ J

The next step - multiply equation (12) on cos в and equation (13) - in sin в , then add the value received. The result is:

— pB to¹ sin в 1 —

B ²

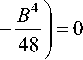
2I ³           . ¹ • n /

A to cos a — AB to I -cos a + — sin в sin( a — в )

B g - qa?--— cos(a — в) = —-—/-------

A to ² 1 — 1 + ³ B ² |

I      8 J

= B cos в q^¹

^— g

+ B 1

— 2 n ^ B to sin в •

Transformations of equations (18) and (19) will have the first equation that links the amplitude A and B :

I 1                      3

A to ² sin a + AB ² to ² - cos( a — в ) — sin a

I 4              8

= B sin в q to¹

—

gB ^{2 1 g +}T

+ 2 n ^ B to cos в .    (13)

B ^(2 n ^T ( B ))² + ( T 2 ( B , to ) T 3 ( B ))² to ² T 1 ( B ) T 3 ( B )

where T 1 ( B ) = 1 — ³ B ² ;   T 2 < B , to ) = g — q to ² — gB- ;

To construct equations (10) – (13), the following intermediate formulas ( y = tot ) are used:

2 n

J sin^{2 n + 1} ( y — в ) sin ( y ) d y = cos в * J ( n + 1 ) ,   (14)

2 n

J sin^{2 n + 1} ( y — в ) cos ( y ) d y = — sin в * J ( n + 1 ) ,  (15)

2 n

J sin(y — a)sin2n (y — в)sinydy = sin в sin (в — a) J (n) + cos (2в — a) J (n +1),   (16)

2 n

J sin(y — a)sin2n (y — в)cosydy = sin(в — a)cosвJ(n) — sin(2в — a) J(n +1) ,   (17)

where J ( n ) =

/ sin² n ( x ) dx = 2 x ^L3 - ⁵ '-( ² n ^— 1 )

J       ^V                     2 ⁿn !

After this, the problem is raised by eliminating unnecessary variables B , a , в and determining the functional dependence of the amplitude A is the steadystate forced oscillations of the carrier body on frequency to .

Multiply equation (12) on sin в and equation (13) -by cos в then subtract the second. As a result, the following equation is obtained:

T 3 ( B ) = 1 — —; 0 ( B , to ) = 8

—ад ^T ( B ^{to )}

T 3 ( B )         to ² T , ( B )

Next step – find the second algebraic equation that relates the amplitude A and B . Raise squared equations (10) and (11), and then add them. Use equation (18) and (19) at intermediate transformations (not given). As a result, we obtain the required equation:

A =

Fo 2 — T52 (B, to) — 2 B T5 (B, to) * 0( B, to) Q2(to) + (2 nxto)2             , where T4(B) = 1 — — — — ; T5

8   48

Q ( to ) = to 0 — (1 + v + ^ ) to ² .

After extracting the amplitude A of the carrier body with equations (20) and (21), we obtain nonlinear algebraic equation with respect to a given implicit function B = B ( to ) in this general form:

Ф ( B ( to ), to ) = 0.                 (22)

The exact solution of the equations of (22) related B = B ( to ) cannot be found, but they can be solved on the basis of approximate numerical methods in the right frequency range. After setting depending B = B ( to ) on the numerical formula (21), it is finally determined by the desired amplitude-frequency characteristic A = A ( to ) damping system with a non-linear tuning pendulum absorber.

To obtain the frequency response of a damping system in a linear formulation [1], it is supposed to be presented in equations (20) – (21):

Ψ ₁( B ) = Ψ ₃( B ) = Ψ ₄( B ) = 1 and Ψ ₂ ( B , ω ) = g - q ω ².

• IV.    Results of Numerical Analisis

For illustration, it fulfils a numerical experiment for three cases: for a damping system with an absorber, it takes into account the nonlinearity in Fig.2; it shows a damping system with an absorber without regard for nonlinearity in Fig.3; it shows a system without an absorber in Fig.4. The parameters of the system and the level of external influence were chosen for practical reasons: L = 2,0 m ; l = 1,5 m ; µ ₀ = 0,03 ; ν = 0,05 ; ω = 1,5 rad / s ; n = 0,45 m / s ; n = 0,03 s ^{- 1}  ;

ϕ x

F ₀ = 0,003 g . The first four parameters were determined for the damping system without regard for nonlinearity following the known methods [6 – 8] and [1], the last two parameters are in accordance with the regulatory documents of the construction industry [9, 10].

Comparing the maximum values of amplitudes for each AFC, the following can be noted. The maximum amplitude for the frequency response of the system, taking into account the nonlinearity (Fig.2), it is 2.35 times smaller than the maximum amplitude for the frequency response of the system without an absorber (Fig.4). With the same parameters, the maximum amplitude on the AFC graph of the system in the linear formulation of the problem (Fig. 3) is 2.56 times smaller than the maximum amplitude for the frequency response of the system without an absorber (Fig. 4).

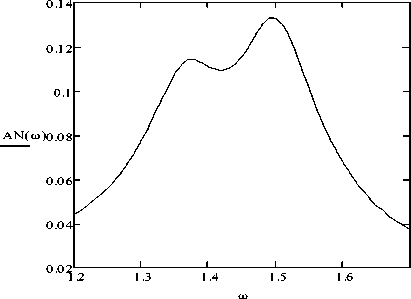
Fig.2. AFC of the damping system with a two-mass pendulum absorber taking into account the nonlinearities

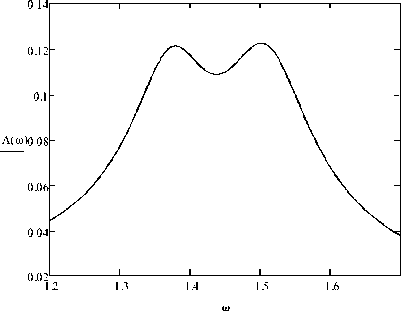
Fig.3. AFC of the damping system with a two-mass pendulum absorber in a linear setting

The presented results of dynamic calculations quantitatively and qualitatively confirm the existing experimental data on a significant decrease on the level of maximum amplitudes when using absorbers on high-rise structures such as aerial masts and TV towers [11, 12].

In addition, it can be noted that the maximum amplitudes on the curves of the amplitude-frequency characteristic (Fig. 2 and Fig. 3) also differ by a factor of 1.09, with a larger amplitude for the system, in which nonlinearities are taken into account in the model. Thus, the optimal tuning of the parameters of the vibration protection system without taking into account its nonlinearities leads to an underestimation of the real maximum amplitude of the forced oscillations of the carrier body. At the same time, for the selected parameters, if the graph of the frequency response of the system for a problem in a linear formulation has a symmetrical form (Fig. 3), which indicates its optimal tuning, then the frequency response of the system in a nonlinear formulation does not have this symmetry (Fig. 2). This indicates that the system parameters are not optimal when the nonlinearities are taken into account. Therefore, the optimal tuning of the system within the framework of the linear model is not optimal within the framework of the nonlinear model. Proceeding from this, it is necessary to develop an appropriate method for determining the optimum tuning parameters of absorbers of this design, which the nonlinearities of the system should be taken into account for the study.

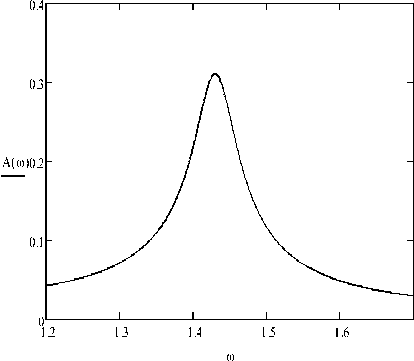
Fig.4. AFC of a mechanical system without an absorber

• V.    С ONCLUSIONS

The proposed system of vibration suppression of forced oscillations of a bearing body allows to significantly reduce the level of vibration amplitudes, and thus to exclude the possibility of the appearance of resonance phenomena in a mechanical system [13]. This conclusion is quantitatively and qualitatively confirmed by existing experimental data on a significant decrease in the maximum amplitudes when using absorbers in this design. The noted result is achieved due to the optimal tuning of the absorber parameters by the corresponding frequencies of the natural oscillations of the specific carrier body. Adjustment of the natural frequency of a two-mass absorber with the help of optimal selection and adjustment of its four main parameters. In addition, in order to implement the optimum tuning of the absorber, it is necessary to introduce a regulated damping element with a variable coefficient of viscous resistance. At the same time, the operating range of natural frequencies (from 0 to 15 rad / s) of such absorbers is wider than in single-mass pendulum damper.

The results of the numerical experiment show a difference between the maximum values of the amplitudes of the carrier body in the linear and nonlinear models. At the same time, there is the larger amplitude for the system, in the model of which nonlinearities are taken into account. Thus, the optimal tuning of the parameters of the vibration protection system without taking into account its nonlinearities leads to an underestimation of the real maximum amplitude of the forced oscillations of the carrier body [14].

Therefore, the development of a methodology for the optimal tuning of the parameters of the proposed absorbers in a nonlinear formulation remains an individual actual practical and theoretical problem.

The results of this research can be used by developers and designers of vibration dampers for forced oscillations of high-rise structures and other extended objects while developing their design solutions.