Non-polynomial Spline Difference Schemes for Solving Second-order Hyperbolic Equations

Published Online August 2011 in MECS

We consider the following second-order hyperbolic equation d2 u

=     + f ( x , t ), 0 <  x <  1, t >  0, (1)

о t subject to initial conditions

u(x,0) = g 1 (x), 0 < x < 1,

^ufe0) = g2 (x), 0 < x < 1,

о t and boundary conditions

u ( 0, t ) = f , ( 1 ), u ( 1, t ) = f 2 ( x ), t >  0 . (4)

The above equations occur frequently in many fields of applied science and engineering; see [1,2,4,6,7] for example Recently, the finite difference schemes for

Eq,(1)were proposed in [3]with the truncation error being o(k2 + hp ) ,where p = 1,2, and k and h denote the mesh parameters for x and t , respectively. Very recently, Rashidinia et al . [5] developed a class of methods based on non-polynomial cubic spline and the truncation error was improved to

o(k2 + h2) and o(k2 + h4 ). They claimed that their schemes are unconditionally stable.

In this paper, we shall first point out that Rashidinia et al .’s schemes are in fact conditionally stable only. Then to improve both the accuracy and the stability of their methods, a new class of spline methods is proposed for Eq. (1) by using a non-polynomial cubic spline function approximation in space direction and finite difference approximation in time direction.

II THE CONDITIONALLY STABILITY OF SPLINE METHODS IN [5]

Let A be a partition of the interval 0 < x < 1 ,which divides[0,1] into N subinterval with the uniform step length h = — .Let K > 0 be the time direction. The N grid points (i,j) are given by xi = ih, i = 0(1)N ,and ti = jk,j = 0,1,2,-... Let u be the approximate value.

In [5], an approximation for Eq. (1)was developed in which the derivative with respect to time is replaced by a finite difference approximation and the derivative with respect to space is replaced by the non-polynomial cubic spline function approximation. Denote du (xi, tj)

^ux ⁽ x i , t j ) = -----------,             ⁽⁵⁾

оx

UxxX^Xi , t, ) = xx j

d ² u ( x i , t j )

6 x ²

where j = 1(1) N — 1.

u t ( ^xi , t j) =

d u ( x i , t j ) d 1

Substituting Eqs.(13)-(14) into (15),they finally obtained the following schemes

/ x    a ² u ⁽ x i , t j )

u,, I x,, t,) =-------- tt i j                    2

^utt ^{( x}i , t j ) =

^{u ( x}i , t j + 1 ^{)— 2 u ( x}i , t j ^{)+ u ( x}i , t j - 1 )

k ²                     ,(9)

+ o ( k ² )

a u /—1 ¹ + 2 p u^{j + 1} + a u^j j1

— ( 2 a + r ) u_i — 1 — ( 4 в — 2 r ^u^ j —

( 2 a + r ) u_i^j _{+ 1} + a u^j i z ! + 2 p u^{j — 1}

j — 1       2 j            j j

^{+ a u}i + 1 = ^k ( P f i — 1 ⁺ 2 P J i ^{+ a} J i + 1 ),

where j = 0,1,2,. „ , i = 1(1) N — 1,

⁵ ;⁽ x i , t j' ⁾= M i + ^o( h ² ) ,      (10)

r = k ²/ h ², a =

_w_ _v sin ( w )

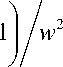
where 5 _д( x , t ) and M^J i are defined in[5].

and

At the gird point ( x i , t j ) ,the given differential equation

(1) was discretized as utt (xi, tj) = Uxx (xi, tj)+ f(xi, tj).     (11)

By putting Eqs.(5)-(11) into Eq.(11),Eq.(11) because

P

^{w cos ( w} ) ' sin ( w ) _v

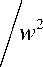
as defined in[5].To achieve the accuracy order

O ( k ² + h ² )

of their schemes,the parameters a

^{u ( x}i , t j + 1 ^{)— 2 u ( x}i , t j ^{)+ u ( x}i , t j - 1 )

k ²

+ O ( k ² )

, (12)

and P were chosen satisfy a + P = 2 .

= M ' + O ( h ²) + f ( x i , t j )

and by neglecting the truncation error, equation leads to

the

above

The authors in [5] claimed that the stability for the difference schemes (16) are unconditionally stable. However, that is not true. In fact, by applying the root condition [9] to the Eq.(21) in [5], a necessary and

sufficient condition for k| <  1 is that

u j + i _- 2 u j ₊ u j - 1

-—ki—— = Mi + f ^j .

Q >  0, Q — ф + v >  0, Q + ф + у >  0 , (17)

Similarly, the following equations hold

M + ^j 1

uM - ^{2 U} + 1 ⁺ uu 2

^j f + 1

M

- 1

Ui-1 — 2 u j _ 1 + u^ k ²

-

f — 1 -

where Q , ф and у are defined in [5].Eq.(17) is equivalent to

Q = a e ^iS + 2 p + a e ^— i⁶ >  0, V ^ e [ 0,2 ^ ],     (18)

Q — ф + у = ( 4 a + r ) e i⁶            _r

Z x z \ V 6 e [ 0,2 n ], (19)

+ ( 8 P — 2 r ) + ( 4 a + r ) e ^— i⁶ >  0,

In [5],the following non-polynomial cubic spline relation was given

^ui + 2 ^{— 2 u}j ^{+ u}j — 1

= h2( aM_i+ , + 2 P Mj + a M J,

Q — ф + у = 2 r ( 1 — cos 6 ) >  0, V 6 e [ 0,2 n ], (20)

Where

a + p = 2             (21)

From Eqs.(18-21),we can get

2 a <  --- ¹—- , V 0 g [ 0,2 п ],     (22)

1 - cos O

( 8 a + 2 r ) <--------- , V O g [ 0,2 n . ] (23)

1 - cos 0

That is,

1   11

a < — • min ------- = —    (24)

2 ° е^[о^{,2 п} ] 1 - cos O 4

r <  min--4 a = 1 - 4 a (25)

^{O G} [ ^{o,2 n} ] 1 - cos O

Therefore Rashidinia et al.’methods[5] are conditionally stable only.

III NEW NON-POLYNOMIAL CUBIC SPLINE METHODS

To obtain some difference schemes with a better stability and accuracy, we can modify scheme (13) into u.+1 - 2ujj + ujj-1

k ²                                     (26)

= a M j +1 + 2в M j + a, M j-1 + f/, 1i                     1i 1i i where a1, P1 are parameters,satisfying a1 + P1 = 2.

Then similar to Eqs.(13-14),we obtain

( a ₂ - a ₁ r )( u^J j + + u j /) + (2 Д + 2 a ₁ r ) u /⁺¹

= (2Дr + 2a2)(ui+ + ui-1) + de -4^1r)ui j-1  111 -Ц_Г?Й jlni-W-1

(^Z 1 r Ca 2 )( u i + 1     u i - 1 ) (2 в 2   2^Z 1 r ) u .

+ k ^{2[ a} 1 ^a 2 ^{( f (} xi - 1 , t j и ) + ^{f (} x - 1 , t j - 1 ))

+ 2 a 2 P i f ( x- 1 , j + 2 a в ( f ( x., t j + 1 )

+ f ( x . , t j - 1 )) + 4 в 1 P 2 f ( x , t j )

^{1 a} 1 ^a 2^{( f (} x . + , t j + 1 ) ^{1 f (} x . + 1 , t j - 1 ))

+ 2a 2 Pi f (x.+1, t7)], where r = k2/ h2,.’ = 1(1)(N - 1), j = 1,2, l, and a2 and P2 are parameters defined in [5].

By choosing suitable values of parameters a^ P^ a2 and P2 ,we ontain various numerical Methods to solve the hyperbolic equation (1).The truncation error and stability analysis of these methods are given in Section 4.

IV TRUNCATION ERROR AND STABILITY ANALYSIS OF THE PRESENT METHODS

Expanding Eq.(27) in Taylor series in terms of u ( x , t_j ) and its derivatives, we obtain the truncation error

T.j = (2a1 + 2в1) -у - (2a 2 + 2Д) -у dxd

• 1             ₂ 6 ⁴ u ₂ d ⁴ u

+ -^ + Д) h — - a 2 h+

• 6            dxd

  - , 2 5 4 u     1               2 d 4 u d 1 k     2.2 A ( a 2 + в 2 ) k -4 d x t    6               d t 1    /    , n M 4 d6 u --( a + в ) h —r+ 180 1     1      d x 6 1          ли d 6 u ( a 2 a r ) h 12 2     1       d x 4 d t 2 , 1 /                     06 u , +-- ( a - a. r ) k —-+—. 180               d t 6

  (28)

• 1 )    If we choose a 1 + P 1 = у and a ₂ + P ₂ = у in (27), we get a scheme of O ( k ² + h ² ) .

• 2 )    If we choose a ₁ + в ₁ = у , a ₂ + P ₂ = у and a ₂ = 1/2 in (27),we get a scheme of O ( k ² + h ⁴) .

• 3 )    If we choose a ₁ + P ₁ = у a ₂ + P ₂ = у and a ₂ = 12 in (27), we get a scheme of O ( k ⁴ + h ² ) .

• 4 )    If we choose

a ₁ + P ₁ = у a ₂ + в ₂ = у , a ₁ = 112 and a ₂ = 112 in

(27),we get a scheme of O( k ⁴ + h ⁴ ).

For various values of parameter a ₁ , a ₂ , P ₁ , P ₂ and

/, the truncation errors may now be obtained. Now we analyze the stability of the scheme (27 ).We assume that solution of (27) at the gird point (Xi, t j) is of the form

0 <  a 1

1          1     1 — 4 a

< — ,0 <  a < — , r < -----²

4       2 4     1 — 4 a 1

.

M = P^ ⁶ ,          (29)

0 <  a 1

< —

1 4 a

, a > -,—²

² 4 4 a

1     1 — 4 a

- <  r < -----²

1 — 4 a ₁

.

Where I= V — 1, 9 is real and £ is, in general,

complex. Substituting (29) into (27), we obtain a characteristic equation

A ^ ² + B ^ + C = 0 ,       (30)

a > —, a

1     1 — 4 a

> —, r < -----²

4     1 — 4 a ₁

.

By

V choosing

A CLASS OF METHODS suitable values of parameters

Where

a_v a 2 , в в ₂

and / , we obtain the following a class

of methods:

A = C = ( a ₂ — a 1 / )cos 9 + в ₂ + a 1 / ,   (31)

1) If we choose a = 0, в = —, a =^— and

1         1 2 2 6

B = — 2Д / cos 9 — 2 a 2 cos 9 — 2 в ₂ + 2 в 1 / . (32)

p 2 = 3 in (27), we get formula of Rashidinia et al. [5]

By applying the root condition [9] to Eq.(30), a necessary and sufficient condition for | ^ <  1 is that A >  0, A + B — C >  0, and A — B + C >  0. From Eqs.(31-32), a 1 + в 1 = у and a ₂ + в ₂ = ₂,^w e have

A + B + C = 2 / (1 — cos 9 ),      (33)

A — C = 0,                    (34)

A — B + C = (2 a ₂ — a 1 / + в/ ) cos 9 + a/ — в 1 / .

Noticing that A + B + C >  0, if / >  0, V 9 e [ 0,2 n ] , we obtain from Eqs. (31) and (35) that

( a ₂ — a 1 / ) cos 9 + в ₂ + a 1 / >  0, V9 e [ 0,2 n ],(36)

with truncation error of 0( k ² + h 2 ) , which

conditionally stable for 0 <  / <  3 .

2) For a = a = ^— and p = p = — in (27),

1      2 6          1      2 3

obtain the conditionally stable

accuracy 0( k ² + h ²) , and 0( k ⁴ + h 4 )

is

we

formula

of

with / = 1 .

• 3)    For a, = —, в = —, a = — and

• ¹    6 ¹ 3 ² 12

(27), we get formula

of 0( k ² + h 4 ) , which

for 0 <  / <  2 .

4) For the choice a ₁ =

в 2 =

with truncation

is conditionally

(2 a 2 — a 1 / + Д / )cos 9             (37)

+ 2 в ₂ + a 1 / — в 1 / >  0, V9 e [ 0,2 n ],

where a 1 + в 1 = -2 and a ₂ + в ₂ = 2 .Hence, we deduce that the scheme (27) is unconditionally stable if

— >  a > — and a < ^_ , and the scheme (27) is

2      1 4        2 4

conditionally stable if

in error

stable

0, в = —, a = — and

1    2 2    12

P ₂ = 12 in (27), we get formula Rashidinia et al.[5]

with truncation error of 0( k ² + h 4 ) , which is

conditionally stable for 0 <  / <  3 .

5) If we choose a = ^_, p = ^_, a 1 3 1 6 2

= — and

в = —

2    12

in (27), we arrive at the unconditionally stable scheme with accuracy 0(k2 + h4) .

6) For a1 = a2 = 12 and p1 = p2 = 12 in (27), we obtain formula of accuracy 0(k4 + h4), which is conditionally stable for 0 < Y < 1.

VI NUMERICAL EXAMPLE AND DISCUSSION

Example: Consider the hyperbolic equation (1) with the initial boundary value conditions (2-4) in

which f1 (t) = f 2(t) = 1 , g 1 (x) = sin(nx) + 1 and g2 (X) = 0 . The average relative error percentage (AREP) is tabulated in Table 1-4 at t = 2.0 with Y = 1 / 3,0.4,2 / 3,1 . The exact solution u(x, t)

and the solution at the first time level u ( x , k ) are respectively given by

u(x, t) = 1 + sin nx cos nt, and

k2

^{u ( x} , k ) = g 1 ^{( X} ) ⁺ kg 2 ^{( X} ) ⁺ — g 1 xx ^{( X} )

.

+ -g 2xx (x) + 0(k 4)

Table 1. The observed average relative error in present methods ( r = 1/3)

( a 1 , p 1, a 2 , p 2^	h = — 16	h = — 32	h = — 64	h = — 128
(1/6,1/3,1/6,1/3)	1.76E(-4)	4.84E(-5)	5.15E(-6)	3.76E(-7)
(1/6,1/3,1/12,5/12)	9.81E(-5)	2.48E(-5)	2.62E(-6)	1.91E(-7)
(1/3,1/6,1/12,5/12)	3.11E(-4)	7.56E(-5)	7.93E(-6)	5.77E(-7)
(1/12,5/12,1/12,5/12)	4.86E(-7)	3.16E(-8)	8.36E(-10)	1.52E(-11)
(0,1/2,1/6,1/3)[5]	3.27E(-4)	9.51E(-5)	1.02E(-5)	7.46E(-7)
(0,1/2,1/12,5/12)[5]	9.08E(-5)	2.44E(-5)	2.59E(-6)	1.89E(-7)

Table 2. The observed average relative error in present methods ( r = 1/4)

( a 1 , P 1 , a 2 , P 2 )	h = — 16	h = — 32	h = — 64	h = — 128
(1/6,1/3,1/6,1/3)	2.48E(-4)	1.04E(-5)	2.78E(-6)	7.09E(-7)
(1/6,1/3,1/12,5/12)	1.77E(-4)	7.68E(-6)	1.90E(-6)	4.76E(-7)
(1/3,1/6,1/12,5/12)	5.58E(-6)	2.48E(-5)	5.82E(-6)	1.43E(-6)
(1/12,5/12,1/12,5/12)	1.82E(-6)	7.46E(-9)	4.75E(-10)	3.00E(-11)
(0,1/2,1/6,1/3)[5]	3.83E(-3)	-	-	-
(0,1/2,1/12,5/12)[5]	4.44E(-4)	7.06E(-6)	1.86E(-6)	4.73E(-7)

Table 3. The observed average relative error in present methods ( r = 2/3)

( a x , Д ,^, Д)	h = — 16	h = — 32	h = — 64	h = — 128
(1/6,1/3,1/6,1/3)	5.66E(-5)	1.54E(-5)	3.99E(-6)	3.53E(-7)
(1/6,1/3,1/12,5/12)	1.33E(-4)	3.21E(-5)	8.06E(-6)	7.11E(-7)
(1/3,1/6,1/12,5/12)	4.71E(-4)	1.01E(-4)	2.45E(-5)	2.15E(-6)
(1/12,5/12,1/12,5/12)	1.92E(-7)	1.26E(-8)	8.05E(-10)	1.78E(-11)
(0,1/2,1/6,1/3)[5]	-	-	-	-
(0,1/2,1/12,5/12)[5]	1.07E(-4)	3.05E(-5)	7.96E(-6)	7.05E(-7)

Table 4. The observed average relative error in present methods ( r = 1)

(av p x , « 2 , P 2 )	h = — 16	h = — 32	h = — 64	h = — 128
(1/6,1/3,1/6,1/3)	1.17E(-16)	1.18E(-15)	5.28E(-15)	1.45E(-14)
(1/6,1/3,1/12,5/12)	2.83E(-5)	1.90E(-6)	1.23E(-7)	7.97E(-9)
(1/3,1/6,1/12,5/12)	2.52E(-4)	1.70E(-5)	1.10E(-6)	7.01E(-8)
(1/12,5/12,1/12,5/12)	1.17E(-16)	1.18E(-15)	5.28E(-15)	1.45E(-14)
(0,1/2,1/6,1/3)[5]	-	-	-	-
(0,1/2,1/12,5/12)[5]	-	-	-	-

It can be seen from Table 1-4 that the results by the present method with accuracy O ( k ⁴ + h 4 ) is much better than that obtained by method in [5], and the schemes in [5] are conditionally stable only.

Acknowledgements

The first author is supported by the Natural Science Foundation of the Anhui Higher Education of China(KJ2011B112).