Nonlinear interaction of the axion field with dynamic aether and Su(2) symmetric gauge field in the anisotropic universe

In the recent papers [1,2] we have formulated the general relativistic theory of nonlinear interaction between pseudoscalar (axion) field, SU(N) symmetric Yang-Mills field and color aether. This theory has been applied to the model, which describes evolution of the anisotropic early Universe in that era, when two phase transitions have just been realized. The first (hypothetical) event was the spontaneous polarization of the color aether, i.e., the event that resulted in the lining up of the SU(N) symmetric vector field multiplet U 。 along the timelike unit vector field U ' attributed to the canonic dynamic aether velocity four-vector [3]. From the mathematical point of view, we considered the relation U ( 。 ) = q ( ° ) U', where q ( 。 ) is the co-vector in the group space, and the subscript ( q ) runs in the range (1,...,N² - 1). The second phase transition, which was assumed in [1,2], could be the parallelization of the Yang-Mills potentials Am) in the group space, ie, A^) = Q ( ^a)A_m. This procedure makes the gauge field quasi-Abelian. In the presented paper we assume that the first phase transition has already taken place, but the second has not yet. In other words, the novelty of this work is that the gauge field is considered to

*The work was supported by the Russian Science Foundation (Grant No 21-12-00130)

be non-Abelian. Also, we consider now the SU(2) gauge group, and we study the non-Abelian SU(2) symmetric analog of the axionically induced generation of the electric field in the magnetized medium (see [4-6] for details).

The paper is organized as follows. In Section 1 we present the theory formalism. In Section 2 we apply this formalism to the Bianchi-I spacetime model, we obtain the model evolutionary equations and formulate the preliminary results of analysis.

• 1.    The formalism

We use the following total action functional:

s = / d%E { ： [ Я+2А+А &《) U ^> -»+JC 欲由 力 _ги^Ь 爪步] +

• + 4 或守 + 4 sin фf 那) 守+ 1% М 。 )-00 ▽* 0 ]} .          (1.1)

Here R is the Ric ci scalar, Л is the cosmological constant, 呂 = 8ttG is the Einstein constant (c = 1), ф describes the pseudoscalar (axion) field; V (ф) is the potential of the axion field. The potential V (ф) is chosen to be of the periodic form V(ф) = 2m^ (1- cos ф). The constant % is reciprocal to the coupling constant of the axion-gluon interactions g^G, i ・ e., 9 ag = 亡. For the multiplet of parallel vector fields the term (U ^ ) U 邸 ) 一 1) transforms into (U ^m U_m- 1) thus providing the vector U ' io be timelike and unit. The constitutive tensor 〈 ；：/ is considered to contain four coupling constants:

心狙)=G(a)(b)仁 1力gm” +C2g，mg” +Сзд，"gm]十 q(a)q(b)C4U'U勺加.

The gauge covariant derivative L)_mU^ can now be reduced to

力mU”a)三 q(a)VmUn + g/(al}{c^q(c)Un .

The t erm ： sin фҒ^ * ”' fj ； ” in the act ion funct ional (1.1) is t he nonlinear periodic generalizat ion of t he term 麺凡 *^ ) 々 *” introduced by Peccei and Quinn [7]. The Yang-Mills field strength tensors f*” and its dual are standardly expressed as follows:

• f*” = V*齒)-V/*) + g/(a^A^A^c), *f'*(a) = 2产sf/sa).(1.4)

Variation with respect to A(a) gives the axionically extended Yang-Mills equations

力* [% +。瓏]=-%/2。)限0*需力*U” .

Keeping in mind three details: first, for the SU(2) symmetry the group constants coincide with the Levi-CiviLa symbols / ( a )⑹( c ) = ^(a)(b)(c)- secomL £ (。)(与(。)气。©)©) = 用般 一用 巧‘： 11 山'工 we work with the Landau-type gauge conditions A* ) U* = 0, we obtain

• Vkflk(a) + gfb^A^f'*(c) = -f(^v*0 - g2C1A'(b)[瑞-q(a)q(b)] .

• 2.    SU(2) model on the Bianchi-I platform

For the illustration, we consider the Bianchi-I anisotropic homogeneous spacetime with the metric

曲2 =必2 — a2(t)d^2 — b2(t)dy2 — c2⑴dz2 .(1.7)

А

v*U” = v”U* = 1g*”,   &三。 *VkU' = 0, ө ⑴ 三 VkU^k = — +^b + -.       ( i.s )

2                                                  q b c

For the illustration of the suggested idea, we consider the class of homogeneous spacetimes with the metric df2 = dt2 - q2(。"/2 - b2«)dg2 - c2«)dz2 .

(2.1)

Generally, this metric describes the Bianchi-I model. When a(t)=b(t)=c(t) we obtain the Friedmann type model. We assume that all the unknown model state functions inherit the spacetime symmetry and depend on the cosmological time only.

In the model with SU(2) symmetry we deal with the triplet of four-vectors A ，) (12 unknown functions). Using the analogs of the Landau gauge / 昭 )U % = 0 we reduce the number of unknown functions to nine. Also, keeping in mind that all the state functions have to depend on the cosmological time only, we are plunging into a new paradigm. In the U(l) symmetric models attributed to the electromagnetic theory we introduced a static magnetic field B q = F12 = const using the nonhomogeneous potentials Л2 = 《 B q /¹, A i = — | B q t². In the SU(2) symmetric model with /胃⑴ we have principally another possibility. We consider the SU(2) symmetric analog of the magnetic field to have the structure F( ， (t) = —g, ；； A2¹ ) (t)A1² ) (t). Assuming that the analog of the magnetic field can produce the analog of the electric field, we have to introduce the potential A,³ ) and thus the electric type term F03) =艰) A33 ) . Also, we consider that q (。)=，如 In other words, our ansatz is that in the model under consideration we can operate with three independent potentials A2¹) (t), A ，) (t) and A33) ( t) ^： the corresponding six non-vanishing Yang-Mills field components are

p(。)_ x(a)0(2) p(。)_X(。)0⑴ ?7(。)_ x(a)0⑶ f 01 — °(2) a1 , f 02 — °(1) A2 ， f 03 — °(3) A3 , f段=-9瑞A21)A12) ,  M3°= 9瑞A12)a33),瓚=-9噌逸以33) .        (2.2)

For this non-Abelian gauge field configuration the equations (1.6) gives three nontrivial equations:

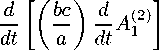
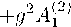
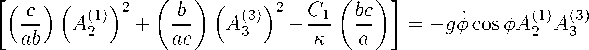
- R ( ^ac )] = - gjcos 0 ^A 1 ^{2) a} 3 ³⁾ ,

d   ac  d dt    b   dt

dt      力 3[ + 9 ² a 3 ³⁾ [( ： ) ( A1² ) )² + (bC —] = -… a 1 ²⁾ a 2 】) .23)

The master equation for the axion field can be now reduced to

富 + 5 [i°g^{( abc )}] 監+從 ^{sin 0} = ( ^^ ) dt [ ^{a 12) a 21) a 33)} ] .            ( 2 」)

The format of this note does not allow us to analyze in detail the equation for the aether velocity four-vector U'. We can only confirm that there exist the solution U'= 品 t 。 the corresponding equation (see [1,2] for details). When we deal with the gravity field equations, we obtain analogs of the equations derived and analyzed in [1,2].

Conclusion

The set of four equations (2.3), (2.4), derived above, describes the SU(2) symmetric model of interaction of the axion and non-Abelian gauge fields. Clearly, when the product A ，) a2" is nonvanishing and thus one deals with the SU(2) analog of the magnetic field 斗 3 ) = 0, the axion field creates the source in the right-hand side of the equation for A33), i.e., the SU(2) analog of the electric field F03 inevitably appears. The profiles of the corresponding solutions will be analyzed in the next work.