Nonlinear viscosity algorithm with perturbation for non-expansive multi-valued mappings

Throughout the paper unless otherwise stated, H denotes a real Hilbert space, we denote the norm and inner product of H by ( .,. ) and norm ||-H , respectively. The set C ( C being a nonempty closed convex subset of H ) is called proximinal if for each x G H , there exists an element y G C such that | x — y | = d(x, C) , where d(x, C) = inf {| x — z | : z G C } . Let CB(D) , K(C ) and P(C ) be the families of nonempty closed bounded subsets, nonempty compact subsets, and nonempty proximinal bounded subsets of C , respectively. The Hausdorff metric on CB (C ) is defined by

H (A, B) = max

< sup d(x, B), x∈A

sup y∈B

d ( y, A ) ,

A,B G CB(C ).

A multi-valued mapping T : C ^ 2 ^C is said to be nonexpansive if H(Tx,Ty) ^ | x — y | for all x, y G C . An element p G C is called a fixed point of T : C ^ 2 ^C if p G Tp . The fixed points set of T is denoted by Fix (T) .

The problem of finding a common element of the set of solutions of equilibrium problems and the set of fixed points for single-valued mappings in the framework of Hilbert spaces

has been intensively studied by many authors, for instance, see [1–5] and the references cited therein.

Ceng et al. [6], introduced the following generalized equilibrium problem with perturbation: Find x* G C such that f (x*,y) + ((A + B)x*,y - x*) > 0 (Vy G C),                   (1.1)

where A,B : C ^ H are nonlinear mappings and f : C x C ^ R is a bifunction. The problem (1.1) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, Nash equilibrium problems in noncooperative games and others [1, 4, 5, 7, 8].

In 2016, Azhini and Taherian [9], motivated by [6, 10], proposed the following iteration process for finding a common element of the set of solutions of variational inequality (1.1) and the set of common fixed points of infinitely many nonexpansive mappings { S _n } of C into itself and proved the strong convergence of the sequence generated by this iteration process to an element of F ( Pc S) = П П=1 F ( Pc S n ) .

^F(u n ,^{y) +} ( ^{(M +} N^)x n , ^{y —} u n ) ⁺ ~^{( y —} u n , u n ^— x n ) ^ ^{0 ( V y G} C ^),

Xn+1 = enPcf (xn) + YnXn + ^nPcSn[anZ + (1 — an)un] (Vn G N), where en + Yn + ^n = 1.

In 2019, Sahebi et al. [11] by intuition from [12–15] considered a general viscosity iterative algorithm for finding a common element of the set general equilibrium problem system and the set of fixed points of a nonexpansive semigroup in a Hilbert space as follows:

^u n,i — T r ni i ^(x n

T ni ^ i X n ),

w n

k

= k Eu n,i , i =1

(1.2)

X n+1 = a n Yf (x n ) + e n Bx n + ((1

— 6 n )I — e n B - a n A) S- s n T(s)W n ds. ⁿ 0

They proved that, the sequence generated by this algorithm under the certain conditions imposed on parameters strongly convergence to a common solution of general equilibrium problem system.

Many authors have shown the existence of fixed points of multi-valued mappings in Hilbert spaces (see [16–19]). The study of multi-valued mappings is much more complicated and difficult than that of single-valued mappings.

In this paper, motivated by the research going on in this direction, we introduce the iterative algorithm for finding a common element of the set of fixed point of a nonexpansive multi-valued mapping in a real Hilbert space. Some strong convergence theorems and lemmas of the proposed algorithm are proven under new techniques and some mild assumption on the control conditions. Finally, some numerical examples that show the efficiency and implementation of our algorithm are presented.

The paper is structured as follows. In Section 2, we collect some lemmas, which are essential to prove our main results. In Section 3, we introduce a new algorithm for finding a common element of the set of fixed point of a nonexpansive set-valued mapping in a real Hilbert space. Then, we establish and prove the strong convergence theorem under some proper conditions. In Section 4, we also give some numerical examples to support our main theorem.

2.    Preliminaries

Let H be a Hilbert space and C be a nonempty closed and convex subset of H . For each point x G H , there exists a unique nearest point of C , denote by Pc x , such that ||x — Pc x | ^ ||x — y | for all y G C . Pc is called the metric projection of H onto C . It is well known that Pc is nonexpansive mapping. Also, a mapping M : C ^ H is said to be monotone, if

( Mx — My,x — y ) >  0 ( V x,y G C ).

M is called α -inverse-strongly-monotone if there exist a positive real number α such that

( Mx — My,x — y ) >  a ^ Mx — My | 2 ( V x,y G C ).

It is obvious that any α -inverse-strongly-monotone mapping M is monotone and Lipschitz continuous.

Recall that a mapping T : H ^ H is said to be firmly nonexpansive if

( Tx — Ty,x — y ) >  ||Tx — Ty l 2 ( V x,y G H ).

It is also known that H satisfies Opial’s condition [20], i.e., for any sequence {xn} with xn ⇀ x, the inequality liminf |xn — x| < liminf |xn — y|                        (2.1)

n→∞         n→∞ holds for every y G H with y = x. The following lemmas will be used for proving the convergence result of this paper in the sequel.

Lemma 2.1 [21] . Let C be a nonempty and weakly compact subset of a Banach space E with the Opial condition and T : C ^ K (E) a nonexpansive mapping. Then I — T is demiclosed.

Lemma 2.2 [22] . The following inequality holds in real space H:

| x + y l < 11x11 2 + 2 ( y,x + y ) ( V x,y G H ).

Lemma 2.3 [23] . Let C be a closed and convex subset of a real Hilbert space H. Let T : C ^ CB(C ) be a nonexpansive multi-valued map with Fix(T ) = 0 , and Tp = { p } for each p G Fix(T ) . Then Fix(T ) is a closed and convex subset of C.

Lemma 2.4 [24] . Let F : C x C ^ R be a bifunction satisfying Assumption 2.1 and let T F be defined as in Lemma 2.5 , for r >  0 . Let x,y G H and t, s >  0 . Then,

T F y — T _t ^F x | ^ | x — y l +

s — t

s

lI T F y — y | .

Lemma 2.5 [25] . Let C be a nonempty, closed convex subset of H and let F : C x C ^ R be a bifunction satisfying Assumption 2.1 . Then for r >  0 and x G H, there exists z G C such that F (z, y) + 1 ( y — z,z — x ) ^ 0 for all y G C. Further define

_{T r} F _x

= (z G C : F(z,y) + ¹ ( y r

—

z, z

—

x ) >  0^

( V y G C )

for all r >  0 and x G H . Then, the following hold: (i) T _r ^F is single-valued.

• (ii)    T _r ^F is firmly nonexpansive, i. e.,

|| T rF (x) ^— T F ⁽y) | ^C ( T F (x) ^— T F ⁽y),x ^— y ) ( V x,y ^E H).

• (iii)    Fix(T f ) = EP(F ) .

• (iv)    EP(F ) is compact and convex.

Lemma 2.6 [26] . Assume that B is a strong positive linear bounded self adjoint operator on a Hilbert space H with coefficient Y > 0 and 0 < p C ||B||- ¹ . Then ||I — pB || C 1 — PY -

Lemma 2.7 [27, 28] . Let C be a closed and convex subset of a real Hilbert space H and let Pc be the metric projection from H onto C. Given x E H and z E C. Then z = Pc x if and only if

( x — z, y — z ) C 0 ( V y E C ).

Lemma 2.8 [29] . Let { x _n } and { y _n } be bounded sequences in a Banach space X and { в _п } be a sequence in [0,1] with 0 < liminf n ,^ в _п C limsup n^^ в _п <  1 - Suppose x n+i = (1 — e n )y n + e n x n for all integers n ^ 0 and limsup _n ^_TO ( | y n₊i — y n| — | x n+i — x n| ) C 0 . Then lmin ,_x ||y n — x n| = 0 .

Lemma 2.9 [10] . Let F : C x C ^ R be a bifunction satisfying Assumption 2.1 and let T F be defined as in Lemma 2.5 , for r >  0 . Let x E H and s,t >  0 . Then,

\\ t ₈ ^F x — i f x | ² C s — tT F (x) — T FF (x),T F (x) — x ) .

Lemma 2.10 [30] . Let { a n } be a sequence of nonnegative real numbers such that a n+i C (1 — a _n )a _n + 6 _n , n ^ 0, where a n is a sequence in (0,1) and 6 _n is a sequence in R such that

• ⁽ⁱ⁾    ^ n =i ^a n = ^ro ;

• (ii)    limsup n^^ aO n ^{C 0 or S} n =i ^d n <  ”.

Then lim n ._x a n = 0 .

Assumption 2.1. Let F : C x C ^ R be a bifunction satisfying the following assumptions:

• 1.    F(x,x) > 0 (Vx E C);

• 2.    F is monotone, i.e., F(x,y) + F(y,x) C 0 (V x E C);

• 3.    F is upper hemicontinuouse, i. e., for each x,y,z E C,

3.    A Nonlinear Iterative Algorithm

limsup F (tz + (1 — t)x,y) C F (x,y). t^G

For each x E C fixed, the function x ^ F (x,y) is convex and lower semicontinuous.

Let C be a nonempty closed convex subset of real Hilbert space H . Let F : C x C ^ R be a bifunction satisfying Assumption 2.1. Let M , N be two a -inverse strongly monotone and β -inverse strongly monotone mappings from C into H , respectively. Recall that the set of all solutions of problem (1.1) is denoted by GEPP, i. e.

GEPP = (x E C : F (x,y) + ( (M + N )x,y — x ) >  0 ( V y E C )}.

Let T be a nonexpansive multi-valued mapping on C into K(H) such that 0 = Fix(T) П GEPP = 0. Also f : C ^ H be a a-contraction mapping and A, B be a strongly positive bounded linear self adjoint operators on H with coefficient Y1 > 0 and Y2 > 0 respectively such that 0 < y < Y1 < y + a, Y1 C II AH C 1 and ||BH = Y2-

Algorithm 3.1. For given x q G C arbitrary, let the sequence { x _n } be generated by:

Г U n = T F (x n — r n (M + N )x n );

(3.1)

[ xn+1 = anYf (xn) + en Bxn + ((1 — Cn)1 — enB — anA)zn, where zn G Tun such that ||zn+i — znH C H(Tun+i,Tun)-

Let { a n }, { в _п }, { e _n } are sequences in (0,1) , { r _n } C [r, to ) with r > 0 satisfied the following conditions:

(C1) lim n^^ a n = 0 , Е^ = to ;

^(C2) limsup n^^ ^e n = 1;

(C3) lim n^^ | r _{n +}i — r n | = 0, liminf n ^^ r _n > 0, 0 < b < r n <  a < 2min { a,e }.

Lemma 3.1. Let p G 0 . Then the sequence { x _n } generated by Algorithm 3.1 is bounded.

• <1 We may assume without loss of generality that a n C (1 — e n — в п Ц В H ) H A H - 1 ■ Since A and B are linear bounded self adjoint operators, we have

||AH = sup{|(Ax,x)| : x G H, HxH = 1}, ЦВЦ = sup{|(Bx,x)| : x G H, HxH = 1} observe that

(((1 — e n )I — e n B — a n Ax,x) = (1 — 6 n ) ( x,x ) — e n ( Bx,x ) — a n ( Ax,x ) ^ ^{1 — e} n ^{— e} n ^H B ^{H — a} n H ^A H ^ ⁰¹

Therefore, (1 — e _n )I — e n B — a _n A is positive. Then, by strong positivity of A and B , we get

^{H (1 — e} n )I ^{— e} n ^{B — a} n A ^H = ^suP {((^{(1 — e} n )I ^{— e} n B ^{— a} n A ^ ^x, x ) ^{x G H}, H x H = ¹ j"

= sup |(1 — e _n ) ( x, x ) — e n ( Bx, x ) — a n ( Ax, x ) : x G H, H x H = 11

(3.2)

(3.3)

^{C 1 — e} n ^{— e} n Y 2 ^{— a} n Y 1 ^{C 1 — e} n Y 2 ^{— a} n Y 1 -

Let p G 0 := Fix (T) П GEPP. Since p G GEPP, from [4, Theorem 3.1] we have

H u n — p H ² C H x n — p H ² + r n (r n — 2a) H Mx n — Mp H ² +r n (r n — 2/3) H Nx n — Np H ² C H x n — p H ² .

Then ||u _n — p || C ||x _n — p||. We obtain

||x n+i - p W = || a n Yf (x n ) + в п Вх п + ((1 - e n )I — в п В — a n A)z n — p ^ C a nh f (x n ) - Ap \ + в п \ Вх п - Bp \ + E n | p | + ^ ((1 — E n )I — в п В — a n A^ H z n — p \\

^{C a} n (\ Y^{f (}x n ) ^— Yf(p) H ⁺ \ Y^f(p) ^— NW) ^{+          —} Bp \ ^{+ E} n \ p \

+(1 — e n Y 2 — a n Y i )d(z n , Tp)

C a n Ya \ x n — p \ + anhf(p) — Ap \ + e n Y 2 ^ X n — p W + a n | p |

+(1 — в п Y 2 — a n Y i )H (Tu n ,Tp)

C anYa\xn — p\ + anhf(p) — Ap\ + 0nY2\Ixn. — pW + an|p|

+(1 — e n Y 2 — a n Y i ) | u n — p \\

^{C (1 — (}Y i ^— Y^a)a n ^{) | x} n ^— p \\ ^{+ a} n ^{( |} p \ ⁺ \ Y^f(p) ^— apID

. J и и \ Y^{f (}p) ^— NW ⁺ IMI 1

C max { |xn — p\,------=}

I                Yi — YaJ

J и и W Yf (p) — Ap W + IM 1

... C max { |xo — p\,------=V

Y i — Ya

Hence { x n } is bounded. This implies that the sequences { u _n } , { z _n } and { f(x n ) } are bounded. >

Lemma 3.2. The following properties are satisfying for the Algorithm 3.1 .

P1. li^m n^^ ^{| x} n+i x n \ — 0 .

P2. lim n ,^ ^W x n t n \   0 .

P3. lim n^^ W Mx n — Mp W = 0 and lim n^^ | Nx n — Np | — 0 .

P4. lim n ,^ ^W x n u n \    0 .

• <1 P1: We have

^W u n+i ^— u n \ = ^{| T} r _{n +} l ^(x n+i ^— r n+i ^{(M + N )x} n+i ) ^— T r n ^(x n ^— r n ^{(M + N )x} n ) ¹

• < ^ (x n+i — r n+i (M + N )x n+i ) — (x n — r n (M + N )x n ) ^

• ⁺    +------- ^{|| T} r _{n +} i ^(x n+i ^— r n + i ^{(M + N )x} n + i ) ^{— (x} n+i ^— r n + i ^{(M + N )x} n + i ^{) |}

r n+i        ⁺

C ^W x n+i ^— x n \ ⁺ | r n+i ^— r n | ^{W (M + N )(x} n+i ^— x n ) ^{W +} --- +------- ^ n+i ,   ⁽3.5)

rn+i where CTn+i - SUPnGN ||Trn+1 (xn+i — rn+i(M + N)xn+i) — (xn+i — rn+i(M + N)xn+i)|.

Setting xn+i — enxn + (1 — en)en, then we have an+iYf (xn+i)+ en+iBxn+i + ((1 — £n+i)I — en+iB — an+iA)zn+i —En+ixn+i en+i — en =----------------------------------:-----------------------------------------

• ^{1    —} C n+i

^a n Y^{f (x} n ) ^{+ e} n ^Bx n ^{+ ((1 —} E n )^{1 — e} n ^{B — a} n ^A)z n ^— E n x n ^{1 — E} n

.. ^an⁺ⁱ (Yf(x n+i ) — Az n+i ) + .. ^an (Az n — Yf(x n )) ^{1 — E} n+i                        ^{1 — E} n

+ / e n+i \1 —E n+i + ( A" — V 1 — E n

1 E ^B (x n+i x n ) + (z n+i z n ) ^ B (z n+i Z n ) + f..                   ) (x n x n+i ). 1 - E n +1                   1 - E n 1 - E n +1

Using (3.5), we have

lkn+1 - e n| <  1 ^an ⁺¹ \b f (x n+1 ) — Az n+1 ^ + —^an— ^ Yf (x n ) — AZ n^ ^{1 — E} n +1                         ^{1 — E} n

^{+ |} z n + 1 ^{— Z} n || ⁺

<

+ ^e n+1

^{1 — E} n +1

в п       в п +1

^{1 — E} n   ^{1 — E} n +1

—

β n

^{1 — E} n

ll^{B || x} n+1 ^— x n ¹

+

^e n+1

1 — E _n +1

a n +1

^{1 — E} n +1

hf ⁽x n+1 )

+

^e n+1

^{1 — E} n+1

+ H (Tu n +1 ,Tu n ) +

+

—

| B || z n+1 — Z n | +

^{1 — E} n +1

^— Az n +1 ^ + ^a n Ц 7/ ⁽x n )

^{1 — E} n

ǫ _n

^{1 — E} n

^{— Az} n ¹1

| X n+1 — X n |

—

β n

^{1 — E} n

β n

—

1 —

ǫ _n

IIB ^{|| x} n+1 ^— x n|

^e n+1

^{1 — E} n+1

| B | H (Tu n+1 ,Tu n )

^E n+1

^{1 — E} n + 1

ǫ _n

—

^{1 — E} n

| X n+1 — X n |

< T~n— ^f( x n+1) ^— Az n+1 ^{1 +} .. ^an ¹¹ Y^{f (}x n ) ^— Az n ¹ 1 — E _n +1                          1 — E _n

+

^e n+1

1 — E _n +1

—

β n

1 — E _n

^{| B || x} n+1 ^— x n h

^{+ |} u n + 1 ^— u n h ⁺

+

e n      e n+1

^{1 — E} n    ^{1 — E} n + 1

^E n +1

1 — E _n +1

ǫ _n

—

1 — E _n

||B||||U n+1 — U n h

| X n+1 — X n |

< -. ^a n ⁺¹ h^f (x n+1 ) ^— Az n+1 ^ ⁺ .. ^an ¹¹ Yf ⁽x n ) ^— Az n ^ 1 — E _n +1                          1 — E _n

β n

1 — E _n

+ | r n+1 — r n | r n+1

^{| x} n+1 ^— x n ^ ^{+ | x} n+1 ^— x n ^ ⁺ | r n+1 ^— r n | ^{|| (M +} N ^)(x n+1 ^— x n ) ¹

e n       e n+1 _

1--1--------- Y2 llxn+1 ^—

1 — E _n    1 — E _n +1

X n | + | r n+1 — Г п |

X ^{|| (M +} N ⁾⁽x n+1 ^— x n ) ^{1 +}

| r n+1 ^— r n |

^ n + 1 I r n+1

+

^E n+1

^{1 — E} n+1

ǫ _n

which implies

^{| e} n+1 ^— e n h ^— llxn+1

X n | <

a n+1

+

α n

+

β n

ǫ _n

ǫ _n

hf (x n ) — AZ n | +

^E n+1

e n+1

β n

^E n+1

ǫ _n

—

1 — E _n

^{| x} n+1 x n ^ l

AZ n+1 |

| X n+1 — X n |

^{+ | r} n+1 ^— r n | ^{|| (M +} N ^)(x n+1

x n

| r n+1 — Г п |

r n+1

^ n + 1

+

e n+1

^E n+1

Y 2 ^|X n+1 — X n | + | r n+1

| r n+1 ^— r n

r n+1

CT n+1^

+

r n | | (M + N )(x n+1

x n ^{) |}

^E n+1

ǫ _n

^E n+1

ǫ _n

||^xn+1     x n^ -

Hence, it follows by conditions (C1)–(C4) that limsup (len+1 — enl — lxn+1 — xnl) < 0.

n→∞

From (3.6) and Lemma 2.8, we get limn ,^ |en — xnl = 0, and then lim lxn+1 — xn| = lim (1 — 6n)len — xnl = 0.

n→∞

P2: We can write

I x n ^— z n l ^ ||^xn+1 ^— x n ¹ + ^{| a} n Yf^(x n ) + ^e n Bx n ^{+ ((1 — C} n )I ^{— e} n B ^{— a} n ^A)z n ^— z n l

^ llx n+1 ^— x n ^{1 + a} n ^ Yf ^(x n ) ^— Az n ! ⁺ B    ^— Bz ^l ⁺ C n h z n h

• < l x n+1 — X n l + a n l Yf (x n ) — AZ n l + e n Y 2 | X n — Z n l + £п|Ы|.

Then

(1 — e n Y 2 ) | x n — Z n ll < l x n+1 — X n l + a nh f(x n ) — AZ n l + C n l z n II-

Therefore lxn —Znl <

<

----1— llxn +1 ^— xn^{1 +    a}n 5 ||Y^{f (x}n) ^— AM ^{+    6}n _ ||zn ^l

1 — e n Y 2                1 — e n e                  1 — e n Y 2

----1— llxn+1 ^— x n| ^{+    a}n - ( H Yf ⁽x n ) ^— AM ^{+ | z} n II) .

^{1 — e} n Y 2                ^{1 — e} n Y 2

Since an ^ 0, ||xn+1 — xnl ^ 0 and (C2) we obtain lim lxn — Znl = 0. n→∞

(3.8)

(3.9)

P3: From (3.3), we have llxn+1 — pl2 = 11 anYf(xn) + enBxn + ((1 — Cn)I — enB — anA)zn — p^

= 11 ^a n (^Yf ^(x n ) ^— A^{p) + e} n ^(Bx n ^{— Bp) + ((1 —} C n )^{1 — e} n B ^{— a} n A^)(z n ^{— p) —} C n p ^

^ ll ^{((1 — C} n ^{)I — e} n ^{B — a} n A^)(z n ^{— p) + e} n ^(Bx n ^{— Bp) — C} n ^p ^

+ 2( a n (Yf (x n ) — Ap), X n+1 — p)

^ ^( 1 — e n Y 2 — a n Y 1 ) d(Z n ,Tp) + e n l B ll X n — Z n l + C n l p l)

+ 2a n (_ Yf (x n ) — Ap,X n+1 — p ) < (( 1 — e n Y 2 — a n Y 1 ) H(Tu n ,Tp) +e n l B ll x n — Z n l + C n l p l) + 2a n < Yf (x n ) — Ap,x n+1 — p ) < C( 1 — e n Y 2 — a n Y 1 )l u n — p l + e n l B ll x n — Z n l + C n l p l)

+ 2a n n ) — Ap, x n+1 — p)

= ( 1 ^{— e} n ^Y 2 ^{— a} n ^Y 1 ) ^{l u} n ^{— p l} 2 ⁺ (^e n ) ^{2 l B l} 2 ^{l x} n ^— z n h 2 ^{+ (c} n ^{) 2 | p | 2 + 2} ( 1 ^{— e} n ^Y 2 ^{— a} n ^Y 1 ) ^e n h ^B hh u n ^— p hh x n ^— z n h

+ 2(1 — e n Y 2 — a n Y 1) C n l p ll u n — p l + 2e n C n l B ll p ll x n — Z n l +2a n Yff (x n ) — Ap, x n+1 — p)

C ( 1 - в п Y 2 - a n Y 1 ) 2 (||x n - p H ² + r n (r n - 2a) ^ Mx n - Mp | 2

+ r n (rn. - 2e )|| Nx n - Np | 2 ) + (в п ) ² П В П 2 П х п - Z n H 2 + (^e n ) ² H p H ²

⁺ 2 ( 1 — ^e n ^Y 2 ^{- a} n ^Y 1 ) ^e n | |B H h u n ^- pllllx n ^- z n h

+ 2 ( 1 - в п Y 2 - a n Y 1 ) ^e n H p HH U n - p H + 2в п б п | В HH p HH x n - Z n H

+ 2a n ^f (x n ) - Ap, x n+1 - p) C H x n - p H ² + (e n Y 2 + a n Y 1) H x n - p H 2

+ ( 1 - e n Y 2 - a n Y i ) 2 ( r n (r n - 2a) H Mx n - Mp | ² + r n (r n - 2e )|| Nx n - Np|| ² )

^{+ (e} n )2 ||B1 12 ||^xn ^{- Z} n ^{| 2 + (e} n ) ²||^pl| ^{2 + 2} ( 1 ^{- e} n ^Y 2 ^{- a} n ^Y 1 ) ^e n ^H B ^HH u n ^{- p HH} x n ^{- Z} n ^H

+ 2(1 - e n Y 2 - a n Y 1) e n H p HH U n - pH + 2e n 6 n | B HH p HH x n - Z n H

+ 2a n ( Yf (x n ) - Ap,X n+i - p ) .

By (C3), we can write

( 1 - e n Y 2 - a n Y 1 ) ² ( r n (2a - r n ) | Mx n - Mp | 2 + r n (2e - r n ) | Nx n - Np H 2 ) C H x n - p H ² - H x n+1 - p H ² + ( e n Y 2 + a n Y i ) 2 H x n - p H ² + (e n ) ² | B H ² H x n - Z n H ² + (a n ) ² H p H ² + 2(1 - e n Y 2 - a n Y 1) e n H B HH u n - p HH x n - Z n H + 2(1 - e n Y 2 - a n Y 1) a n H p HH u n - p H + 2e n 6 n | B HH p HH x n - Z n H + 2a n n ) - Ap,X n+1 -^p)

^C ( ^H x n ^{- p H + H} x n+1 ^{- p |} ) ^H x n ^- x n+1 ^{H +} ( ^e n ^Y 2 ^{+ a} n ^Y 1 ) ^H x n ^{- p H} 2 ^{+ (e} n ^{) 2 | B H} 2 ^{H x} n ^- z n ^{| 2 + (a} n ^{) 2}||^p||^{2 + 2} ( 1 ^{- e} n ^Y 2 ^{- a} n ^Y 1 ) ^e n ^{| B HH} u n ^{- p HH} x n ^- z n ^H

+ 2(1 - e n Y 2 - a n Y 1) a n H p HH u n - p H + 2e n 6 n H ^B HH p HH X n - Z n H

+ 2a n (Yf (x n ) - Ap,X n+1 - p¹).

By a n ^ 0 , H x n+1 - x _n | ^ 0 and ||x _n - Z _n | ^ 0 , then we obtain ||Mx _n - Mp H ^ 0 and ||Nx _n - Np | ^ 0 as n ^ to .

P4: Since p G 0 , we can obtain

^H u n ^{- p H} 2 C ^H x n ^{- p H} 2 ^{- H} u n ^- x n ^{| 2 + 2r} n ^H u n ^- x n ^H ( ^{| Mx} n ^{- Mp H + H} N^x n ^{- Np H} ) •

It follows from (3.9) that

H x n+1 - p H ² C ( 1 - e n Y 2 - a n Y 1 ) ² | U n - p H ² + (e n ) ² | B H ² H x n - Z n H ² + (^e n )² HpH ²

^{+ 2} ( 1 ^{- e} n ^Y 2 ^{- a} n ^Y 1 ) ^e n ||B^H ||u n ^{- p |H}x n ^{- Z} n ^H

+ 2 ( 1 - e n Y 2 - a n Y 1 ) e n | p HH U n - p H + 2e n 6 n | B HH p HH x n - Z n H

+ 2a n( Yf (x n ) - Ap, x n+1 - p¹)

^C ( 1 ^{- e} n ^Y 2 ^{- a} n ^Y 1 ) (^H x n ^{- p H} 2 ^{- H} u n ^- x n ^{| 2}

+2r n | u n - x n H(H Mx n - Mp H + H Nx n - Np H)) + (e n ) ² H B l|²H x n - Z n H ²

^{+ (6} n ^{) 2}||^p||^{2 + 2} ( 1 ^{- e} n ^Y 2 ^{- a} n ^Y 1 ) ^e n ^{| B HH} u n ^{- p HH} x n ^{- Z} n ^H

+ 2(1 - e n Y 2 - a n Y 1) e n H p HH U n - p H + 2e n 6 n | B HH p HH x n - Z n H

+2a n( Yf (x n ) - Ap, x n+1 - p).

Therefore

( 1 - в п Y 2 - a n Y 1 ) ² ^ U n - X n ^ ² C ||x n - p H ² - l|x n+1 - pH ² + ( в п 7 2 + a n Y 1 ) 2 ^ X n - p|| ² + 2r n ( 1 - e n Y 2 - a n Y 1 ) ² | u n - X n \ ( \ MX n - Mp ^ + | NX n - Np |) + (в п ) ² | B | ² | x n - Z n l ²

⁺ (⁶ n ) ^{2 | p | 2 + 2} ( 1 ^{- e} n ^Y 2 ^{- a} n ^Y 1 )     B ^{|| u} n ^{- p || x} n ^- z n \

+ 2(1 - e n Y 2 - a n Y 1) 6 n H p || U n - p ^ + 2в п 6 п|| В||||р||||Х п - z^

+ 2a n( Yf (X n ) - AP, X n+1 - P>

C (| x n - p | + | X n+1 - p |)| x n - X n+1 | + (e n Y 2 + a n Y 1 ) ² | X n - p | ²

+ 2r n ( 1 - e n Y 2 - a n Y 1 ) ² | U n - X nK ^ MX n - Mp | + | NX n - Np | ) + (e n ) ² | B | ² | X n - Z n | ² +(^e n ) ² | p | ² + 2(1 - e n Y 2 - a n Y 1 )e n | B || u n - p^X n - Z n |

+ 2 ( 1 - e n Y 2 - a n Y 1 ) 6 n | p || U n - p | + 2e n 6 n|| B||||p||||X n - z n| + 2a n (X n ) - Ap,X n+1 - p\

Since an ^ 0, ||xn+1 - xn| ^ 0, |Mxn - Mp| ^ 0, |Nxn - Np| ^ 0 and |xn - zn| ^ 0 as n ^ to and we obtain lim |xn - un| = 0.                                (3.10)

n→∞

Using (3.8) and (3.10), we obtain | z _n - u n ! C | z _n - x n ! + | x _n - u n ! ^ 0 , as n ^ to . Then lmi n ,_x | z n - u n| = 0 . ▻

4.    Strong Convergence Algorithm

Theorem 4.1. The Algorithm defined by (3.1) convergence strongly to z E Fix(T ) П GEPP, which is a unique solution in of the variational inequality ( (Yf - A)z, У - z ) C 0 for all y E 0 .

• <1 Let s = P q . We get

^{| s(I -} A ⁺ Yf ^{)(x) - s(I -} A ⁺ Yf⁾⁽У^{) | C} ll(I ^- A ⁺ Yf ^{)(x) - (I -} A ⁺ Yf⁾⁽У^{) |}

^C III ^- A ^{|| x -} y ^ ⁺ Yf^{(x) - f}(y^l ^{C (1 -} Y 1 ^{) | x -} y h ⁺ Y^{a | x -} y h

= ^{(1 - (}Y 1 ^- Y^{a)) | x -} y ^ .

Then s(I - A + Yf ) is a contraction mapping from H into itself. Therefore by Banach contraction principle, there exists z E H such that z = s(I - A + Yf )z = P Fix ( T ) п ерр ( 1 - A + Yf )z .

We show that ((Yf - A)z,xn - z) C 0. To show this inequality, we choose a subsequence {xni} of {xn} such that limsup ((Yf - A)z,Xn - z( = lim ((Yf - A)z,Xni - z(-             (4.1)

n→∞                  ^{i →∞}

Since { x n i } is bounded, there exists a subsequence { x ni. } of { x n i } which converges weakly to some w E C . Without loss of generality, we can assume that x n i ^ w . Now, we prove that w E Fix (S) П GEPP. Let us first show that w E Fix (S) . From | x _n - u _n | ^ 0 , we obtain u n i ^ w . On the other hand lim n ,^ | z _n - u _n | = 0 and by Lemma 2.1, I - T is demiclosed at 0 . Thus, we obtain w E Fix (T) . We show that w E GEPP. Since u _n = T r n (x _n - r _n (M + N )x _n ) . we have

^F(u n , ^{y) +} ( ^{(M + N )x} n , ^{y -} u n ( ⁺ ~^y) ^- u n , u n ^{- x} n ( ^ ⁰ ( V ^{y E} C)•

It follows from the monotonicity of F that

((M + N )x n ,y

u n

( ⁺ 7" ( y r _n

u n , u n

x n

) >  F(y,u n ( V y E C )

which implies that

((M + N )xn ,y

r

u n i

) + — r n i

y r u n _i

, u n _i

r

x n i

) >  F(y,u n ) ( V y E C ).

Let ut = ty + (1 — t)w for all t E (0,1]. Since y E C and w E C, we get ut E C. It follows that ut r uni,

(M + N)u_t) >  (ut

u n i ^,

(M + N )u t ( — ( u t

u n i ^,

(M + N )xn^

r

u t

r

u n i ,

u n i

r

x n i

r n i

^ + F (u t ,u n ) = ( u t

r

u n i ,

(M + N)u t r (M + N)u_ni)

+ u t

r

u n i ,

(M + N )u_ni

r

^{(M + N)x}n₄ ( — ^^ut

r

u n i ,

u n i

r

x n i

r n i

^ + F (u t ,u n i )

Since 11 u n i

r

x n i

= u t r u n _i

+ u _t r u _{n i}

r

, M u t

, M u n i

u t

r

r

r

Mu n _i + u t

Mx ni) + (u t

u n i ^,

u n i

r

x n i

r n i

r

r

u n _i

u n i

, Nu t

, N u n i

r

Nu n i

r

^Nx n i )

|| ^ 0 , we have ||Mu _n i

r

^ ^{+ F(u} t , u n i ) •

Mx n i || ^ 0 and ||Nu n i

r

Nx n i II ^ 0 .

Further from monotonically of M and N , we obtain ut r uni

, M u t

r

Mun) >  0,

u t r u n _i

, N u t

r

Nun) >  0,

so as i ^ to from Assumption 2.1, we have (u _t

r

w, (M + N)u_t) >  F(u t ,w) .

Therefore

0 = F(u t , u t ) <  tF(u t , y) + (1 r t)F(u t , w)

< tF(ut, y) + (1 r t)(ut r w, (M + N)ut) < tF(ut, y) + (1 r t)t(y r w, (M + N)ut), then 0 < F(ut,y) + (1 r t)(y r w, (M + N)ut).

Letting t ^ 0 , we obtain 0 <  F(w, y) + ( y r w, (M + N)w ) . This implies that w E GEPP.

Now from Lemma 2.7, we have lim sup ((Yf r A)z, Xn r z) < limsup (Qff r A)z, xni n→∞                   i→∞ r z) = ((Yf r A)z, w r z) < 0. (4.2)

Now we prove that x _n is strongly convergence to z .

It follows from (3.3) that

||x n+1 - z ^ ² = “ n( ff (x n ) - Az, x n+1 - z^ + вп(Bx n - Bz, x n+1 - z)

• ^- € n ( ^z, x n +1 ^- z ^ + ^((1 ^{- e} n )I ^- 3 n ^{B - a} n ^A ) ^(z n ^- z)>x n+1 ^{- z}^

C a n (y ( f (x n ) - f (z),X n+1 - z ) + Ы' (z) - Az,X n+1 - z)) + P nW || x n - z || x n+1 - z |

• ^{- 6} n ^{| z |} \x n+1 ^{- z} \ ⁺ II^{(1 - e} n )I ^- B ^{- a} n ^{A |} ||^z n ^{- z} W 11x n+1 ^{- z} \

C a n (y ( f (x n ) - f (z),X n +1 - z ) + ( ff (z) - Az,X n+1 - z)) + P n W B || x n - z || x n+1 - z \

• ^{- e} n ^{| z || x} n+1 ^{- z} W ⁺ IK^{1 - e} n )I ^- 3 n ^{B - a} n ^{A | d(z} n ^{,Tz) | x} n+1 ^{- z} \

C a n (y ( f (x n ) - f (z),X n +1 - z ) + ( Yf (z) - Az,X n+1 - z)) + в^Б || x n - z || X n+1 - z \

• ^{- e} n ^{| z || x} n+1 ^{- z} W ⁺ IK^{1 - e} n )I ^- 3 n ^{B - a} n ^A \ H (Tu n , ^Tz) llx n+1 ^{- z} \

C a n aY \ x n - z \ ||x n+1 - z \ + a n Yff (z) - Az, x n+1 - z) + в л вН^ - z H ||x n+1 - z \

^{- e} n|| ^{z |}| ^{| x} n+1 ^{- z} \ ^{+ (1 - e} n Y 2 ^{- a} n f 1 ) ^{| x} n ^{- z} \ 11 x n+1 ^{- z} \

= (1 - a n (Y 1 - af)) | x n - z || x n+1 - z \ - 6 n|| z||||x n+1 - z \ + a n Yff (z) - Az, x n+1 - z) C   ^a n ^{(Y 1} — (| x n - z | ² + | x n+1 - z | ² )- 6 n | z || x n+1 - z||+a n ( ff (z) - Az,x n+1 - z ) C ¹— ^a n 2 — | x n - z | ² + 2||x n+1 - z | ² - 6 n | z || x n+1 - z | + a n ( Yf (z) - Az,x n+1 - z(.

This implies that

2 ^{| x} n+1 ^{- z | 2} C ( 1 ^{- a} n ^(Y 1 ^{- a}Y) ) ^{| x} n ^{- z | 2 + | x} n+1 ^{- z | 2} - 2a n | z || x n+1 - z | + 2a n (f( (z) - Az,x n+1 - z>.

Then

||x n+1 - z | ² C (1 - a n (f 1 - af)) | x n - z | ² - 2a _n | z || x _{n +}1 - z | ^{+ 2a} n ( f^{f (z) - Az}, x n + 1 ^{- z} ^ = ^{(1 -} k n ) ^{| x} n ^{- z | 2 + 2a} n l n ,

(4.3)

where k n = a n (f 1 - af) and l n = (ff(z) - Az, x n+1 - z> - | z || x n+1 - z | .

Since lim _n ^^ a n = 0 and X n=Q a _n = to , it is easy to see that lim _n ^^ k _n = 0 , X n=o k _n = ^TO and limsup n^^ l _n C 0. Hence, from (4.2) and (4.3) and Lemma 2.10, we deduce that x _n ^ z , where z = P @ (I - A + ff )z . >

Remark 4.1. Putting A = B = M = N = 0 , f = 1, we obtain methods introduced in [31, Theorem 3.1].

5.    Numerical Examples

In this section, we give some examples and numerical results for supporting our main theorem.

All the numerical results have been produced in Matlab 2017 on a Linux workstation with a 3.8 GHZ Intel annex processor and 8 Gb of memory.

Example 5.1. Let H = R , the set of all real numbers, with the inner product defined by ( x,y ) = xy for all x,y G R , and induced usual norm | . | . Let C = [0, 2] ; let F : C x C ^ R be defined by F(x,y) = (x - 4)(y - x) for all x,y G C ; let M, N : C ^ H be defined by M(x) = x and N(x) = 2x for all x G C , such that <5 = 2 and в = 3 respectively, and let for each x G R , we define f (x) = 8 x , A(x) = 2x , B(x) = 3 x and

T J

Tx =

{ x } ,     0 C x C 1;

{ 2 } ,     1 C 2.

Then there exist unique sequences {xn} C R and {un} C C generated by the iterative schemes un = TF (xn - rn(M + N)xn);

(4.4)

x n +1 = (8П ⁺ 3П 2) x n ⁺ (G "  2^ 2 1-3)I "  П 2 B — П^A)^{Zn,         (}4.⁵⁾

where a n = n , в п = n2 , ^ n = 2^2—3 and r n = 1 . Then { x n } converges to { 1 } E Fix (T) n GEPP.

It is easy to prove that the bifunction F satisfy the Assumption 2.1. Further, f is contraction mapping with constant a = 5 and A is a strongly positive bounded linear operator with constant Y 1 = 1 on R . Therefore, we can choose 7 = 1 which satisfies 0 <  y <  ^Y 1 < Y + 01 . Furthermore, it is easy to observe that Fix (T) = [0,1] and GEPP = { 1 } . Hence Fix (T) П GEPP = { 1 } = 0 . After simplification, schemes (4.6) and (4.7) reduce to u _n = 2 — x n .

_      \{2 — X n } , 0 ^ U n ^ 1 or (1 ^ X n ^ 2);

Tu _n =

({ 2} ,      1 n ^ 2 or (0 <  X n < 1).

If z _n = 2 — x _n for x _n E [1, 2] , we have

X n +1 ⁼

17    2

- ^{1 +} 8n ⁺ 3П 2 ⁺

2П 2 ¹—3) x n ^{+ 2}G -

1         1     2

2n ² — 3   3n ²    n

If z _n = 2 for x _n E [0,1) , we have

X n +1 ⁼

(±+ 1 V + 1Л — 8n   3n ²        2

2n ² — 3

1 3n ²

-)■ n

Following the proof of Theorem 4.1, we obtain that { x _n } , { u _n } converges strongly to w = { 1 } E Fix (T) П GEPP as n ^ to .

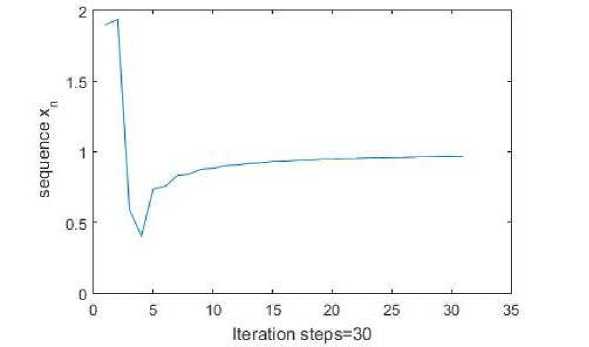
Fig. 1. The graph of { x _n } with initial value x 1 = 1 .

Example 5.2. Let H = R , the set of all real numbers, with the inner product defined by ( x, y ) = xy for all x,y E R , and induced usual norm | . | . Let C = [ — 1, 3] ; let F : C x C ^ R be defined by F (x, y) = x(y — x) for all x,y E C ; let M,N : C ^ H be defined by M (x) = 2x and N (x) = 3x for all x E C , such that <5 = 3 and в = 4 respectively, and let for each x E R , we define f (x) = 6 x , A(x) = X , B(x) = 10 x and

J{ X } ,    0 < x <  3;

({0 } ,       — 1 ^ x ^ 0.

Then there exist unique sequences {xn} C R and {un} C C generated by the iterative schemes un = TF(xn — rn(M + N)xn); (4.6)

^x n ⁺¹ = (Xn ⁺ юХиХ^x n ⁺ (0 - n²)I - (Xi) ² B ^— XA) z n ^{, (4}-⁷⁾ where a n = ^= , в п = (_п-1₁) 2 , ^€ n = n 2 and r n = 1 + n • Then {x n } converges to {0} G Fix (T) П GEPP.

It is easy to prove that the bifunction F satisfy the Assumption 2.1. Further, f is contraction mapping with constant a = 5 and A is a strongly positive bounded linear operator with constant Y 1 = 1 on R . Therefore, we can choose y = 2 which satisfies 0 < Y <  Y1 < Y + a • Furthermore, it is easy to observe that Fix (T) = { 0 } and GEPP = { 0 } . Hence Fix (T) П GEPP = { 0 } = 0 . After simplification, schemes (4.6) and (4.7) reduce to

/ — 4n — 5

V 2n + 1

x n ^,

u n

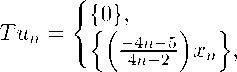
— 15 <  u _n < 0 or (0 < x n <  3);

0 <  u _n ^ 2 or ( — 1 <  x n <  0).

If Zn = 4n+25 Xn for Xn G [—1, 0], we have xn-1 =

(3V n ⁺ 10(n + 1)²) ^{X n +} 0

—

n ²

10(n + 1) ²

—

1 2 V n

X

— 4n — 5

4n + 2

x n ^.

If zn = 0 for xn G (0, 3], we have xn-1 =

(1 +

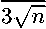
10(n + 1) ²

)

x n ^.

Following the proof of Theorem 4.1, we obtain that { x _n } , { u _n } converges strongly to w = { 0 } G Fix (T) П GEPP as n ^ to .

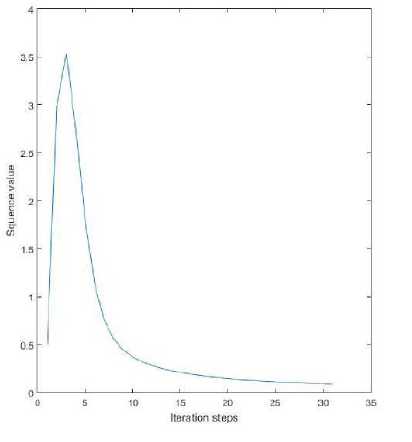
Fig. 2. The graph of { x _n } with initial value x i = 1 .

Acknowledgments. The author would like to thanks the referees for their remarks that helped us very much in revising the paper.