Нормированные системы и их применение к построению решений дифференциальных уравнений дробного порядка

Введение. В настоящей работе мы рассмотрим операторный метод построения решений дифференциальных уравнений дробного порядка. Данный метод основан на построении нормированных систем относительно операторов дробного дифференцирования. Метод нормированных систем был введен в работе [1] для построения точных решений уравнения Гельмгольца и полигармонического уравнения. В дальнейшем метод нормированных систем использовался для решения задачи Коши для обыкновенных дифференциальных уравнений с постоянными коэффициентами [2], для построения полиномиальных решений задачи Дирихле для бигармоническо-го и полигармонического уравнения [3–5], а также при построении решений дифференциальных уравнений, связанных с операторами Данкла [6, 7].

Пусть L ₁ и L ₂ – линейные операторы, действующие из функционального пространства X в X : L k X с X , k = 1,2, и пусть функции из X определены в области Qc R ⁿ . Обозначим N 0 = N и { 0 ] . Приведем определение нормированных систем [1].

Определение 1. Последовательность функций { f_k ( x ): k е N 0 , f_k ( x ) е X } называется f -нормированной относительно ( L 1 , L 2 ) в области Q , имеющей основание f ₀( x ), если везде в этой области

L i f о ( x ) = f ( x), L i fk ( x ) = L 2 fk - 1 ( x), k е N .

Систему функций f -нормированную относительно ( L 1 , I ) , I -единичный оператор будем называть f -нормированной относительно оператора L ₁ , т.е.

L i f о ( x ) = f ( x ), L i f_k ( x ) = f k - i ( x ), k е N .

Если f ( x ) = 0, то систему функций { f_k ( x ): k е N ₀, f_k ( x ) е X } назовем просто нормированной.

Основные свойства системы функций f -нормированной относительно ( L q , L ₂ ) в области Q изложены в работе [8]. Приведем некоторые из них

Свойство 1. Пусть система функций {fk (x): k е Nо} является f -нормированной относительно (L^,L2) в Q с основанием f0(x). Тогда функциональный ряд u (x) = £ fk (x), x еQ                                 (i)

k = 0

является формальным решением уравнения

• ( L q - L 2 ) u ( x ) = f ( x ), x еQ .                                   (2)

Свойство 2 . Если операторы L ^ и L 2 коммутируют, а система функций { f k ( x ): k е N ₀ } является f -нормированной относительно оператора L ₁ в Ω, то формальное решение уравнения (2) можно записать в виде ^

• У ( x ) = £ L 2 fk ( x ), x еQ .                               (3)

k = 0

Свойство 3. Пусть операторы L1 и L2 коммутируют, а система функций {fk (x): к е N0} яв ляется f -нормированной относительно оператора L1 в Q. Тогда система функций

^

Фк (x) = Z n=к

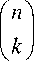
СТf ( x ), x е Q ,

n

У k )

n !

к !( n - к )!

является f -нормированной относительно оператора L 1 - L ₂ в Q.

Построение нормированных систем для некоторых классов операторов

В этом пункте мы приведем методику построения нормированных систем для некоторых классов операторов.

Определение 2. Оператор D p называется обобщенно-однородным порядка в относительно переменной t , если

D p t ^M = Ср, У^p , t >  0                                 (5)

где в , це R ,0 < в < ц , С р^ — постоянные.

Умножим равенство (5) с двух сторон на одночлен t ^{- ц + в} . Тогда С р_ц = t ^{- ц + в} D в t ^ц . Пусть s е R и к одночлену t ^{p k + 5} можно применить оператор D p . Рассмотрим коэффициенты

С ( в , s , i ) = П ( t ^{- p k - 5 + в} D p t ^{в k + 5} ) , i >  1, С ( в , s ,0) = 1. к =1^{v               в} j

Для коэффициентов С ( в , s , i ) имеет место равенство

С ( в , s , i )

( t ^{- в к - s} D _в t ^{в k + p + s} )

С ( в , s , i + 1)

Замечание 1. При определении коэффициентов С (в, s, i) для удобства мы приняли С (в, s ,0) = 1. В конкретных случаях операторов С (в, s ,0) можно выбрать произвольным обра- зом.

Рассмотрим систему функций

tPi-vs fi(t) = С (в, s ,i)

.

Лемма 1. Пусть Dp является обобщенно-однородным оператором порядка в относительно переменной t и для некоторых s е {s1, s2,

...,

^s m ^}, ^s j ^е R , j = ¹,^2,

...

, m выполняется равенство

D p t ^s = 0. Тогда система функций (7) является 0 - нормированной относительно оператора D p .

Доказательство . По определению оператора D p имеем D p / " = ( t ^{- ц + в} D в t ^ц ) t ^{ц - в} . Тогда

D p f ) ( t ) = 0 и для всех s е { s 1 , s ₂,

...

, s m }, s j е R и i >  1 выполняется равенство

D_Bt ^p i ^{+ s}

D p f ' ( t ) = т в тх

С ( в , s , I )

( t ^{- в+в - s} D _в t ^в i ^{+ s} )

С ( в , s , i )

, P i + s - в t .

Далее в силу равенства (6) имеем

( t ^{- в + в - s} D _в t ^{в i + s} )

С ( в , s , i )         С ( в , s , i - 1),

i >  1. Следовательно,

t ^p i ^{- 1} ) ^{+ s}

Dpfi ( t ) =    —— = fi - 1 ( t ). Лемма доказана.

С ( в , s , i - 1)

Рассмотрим функцию

^

ysp (t)=z %-p i=p

^ i \ t Pi + s

I---------- , p е N ₀ .

У p ) С ( в , s , i )

Справедливы следующие утверждения.

Математика

Теорема 1. Пусть p = 0, ряд (8) сходится и к нему можно почленно применять оператор D p .

Если существует значение параметра s , при которых выполняется равенство

( t-^e - ^{s + e} D _e t ^e i ^{+ s} )|

= 0,

то функции y_{s 0} ( t ) при всех таких значениях параметра s удовлетворяют уравнению

В р У ( t ) = Л ( t ).                                      (9)

Теорема 2. Пусть ряд (8) сходится и к нему можно почленно применять оператор Dp. Если существует значение параметра s, при которых выполняется равенство

(t ~ в-s+eDete+s )| = 0, то функции ys p (t) при всех таких значениях параметра s, и для всех p = 0,1, n-1 удовлетво-

ряют уравнению

( D e ^{- Л} ) y ⁽ t ) = 0.

Доказательство этих теорем следует из утверждения леммы 1 и свойств нормированных систем.

Пример. Для любого а >  0 следующее выражение

t

J ^a u ( t ) =-----j ( t - т ) ^{а - 1} u ( т )d T

Г ( а ) 0

называется оператором интегрирования порядка а в смысле Римана-Лиувилля [9].

Пусть m -1 < а< у< m,m = 1,2,.... Рассмотрим дифференциальный оператор дробного поряд- ка следующего вида

m

D'-' u ( t ) = J ^Y-а —J^m чу ( t ). dt ^m

Отметим, что для некоторых частных значений параметра у мы получаем известные операторы дробного дифференцирования. Так в случае у = а имеем D “’“ u ( t ) = RL D ^a - оператор дифференцирования порядка а в смысле Римана-Лиувилля, в случае у = m получаем, что D ^{а ,} m u ( t ) = _CD ^а - оператор Капуто, а в случае у = в ( m - а ) + в ,0 <  в <  1 имеем D^u ( t ) = J ^{в ( m -а} ) — J ^{(1 - в )( m -а} ) u ( t ) - оператор Хилфера [8].

dt ^m

Непосредственным вычислением можно показать, что оператор D ^⁷ удовлетворяет следующим равенствам

D^t⁸ = 0, s = у - 1, у - 2,..., у - m , и D ^^ t ^ = ^{Г ( ц +} 1) t ^ц-а , ц >  m - 1.

Г(ц +1 - а)

Следовательно, D ^{a , Y} является обобщенно-однородным оператором порядка а .

Из утверждений теорем 1 и 2 вытекают следующее.

Следствие 1 . Пусть m - 1 <  а < у <  m , m = 1,2,..., s = у - 1, у - 2,..., у - m . Тогда функции

~ а ' + s

У ( t ) = У Л---t------ ^s    t0 Г ( а к + s + 1)

являются линейно независимыми решениями дифференциального уравнения дробного порядка D ^a ’ ^Y y ( t ) - Л у ( t ) = 0, t >  0.                                   (11)

Следствие 2. Пусть m -1 < а < у < m, m = 1,2,..., s = у -1, у - 2,...,у - m. Тогда для всех значе ний s = у - 1,у - 2,..., у - m и p = 0,1,..., n -1 функции

^ y s.p ( t ) = Z Л - ^p i = p

I \       ta i + s

p) Г(ак + s +1)

являются линейно независимыми решениями дифференциального уравнения дробного порядка

( D " ^у - Я ) n y ( t ) = 0, t >  0.

Функцию ys (t) из (10) можно представить в виде yk (t) = tY- kEaу- k+1(Яt"), k = 1,2,..., m,

∞ zi где E„ RZz) = V-------- в ’ 2 r(ai + в)

- функция типа Миттаг-Леффлера [9]. Так как Ea ^(z) является целой функцией, то отсюда легко получить сходимость рядов из представлений (10) и (12).

Отметим, что фундаментальные решения уравнения (11) в случае у = в(m - ") + в,0 < в < 1, т.е. для уравнения с оператором Хилфера, были построены в работе [10].

3. Построение нормированных систем для неоднородного уравнения

Теперь приведем пример f -нормированной системы относительно оператора D" и по- строим решение неоднородного уравнения

( D " - Л ) n y ( t ) = f ( t ), t >  0

Пусть E"^,t ) = 2 Я ^p [ i 1    t "   , p = 0,1,....

,         i = p     ( p J Г ⁽ г а + a )

Рассмотрим следующую функцию

У р ( f )( t ) = j ( t - T ) ^{a - 1} E P a ( -Я (t - т ) " ) f ( t ) d T .

Теорема 3. Пусть m -1 < a< у< m, m = 1,2,.... Тогда функции yp(f)(t),p = 0,1,... образуют f -нормированную систему относительно оператора D" ,у - Я, то есть справедливы равенства

( D " ’ ^у - Я ) y 0 ( f )( t ) = f ( t ), ( D " ’ ^у - Я ) y p ( f )( t ) = f p - 1 ( t ), p >  1

Доказательство. В случае p = 0 имеем E^ ( - Я ( t - т ) " ) = E _aa ( - Я ( t - т ) " ). Тогда равенство (15) для случая p = 0 доказывается, как и в случае оператора Римана - Лиувилля [8].

Пусть p > 1. Применяя к функции yp (f) (t) оператор Jm у, имеем tτ

J m " p ( f )( t ) = ,         (( t - т ) ^m -^Y ' J ( T - 4 ) " ^{- 1} E p „ ( ЯТ - 4 ) " ) f ( 4 ) d { d r =

r ^{( m -} у Н         0

tt

=           f f ( 4 )J( t - T ) m - ^{Y 1} <  T - 4 ) " ¹ E^{P p} a ( Я ( т - 4 ) " ) d r d i .

r ^{( m} - y ) ^     4

Используя представление функции E"p a, для внутреннего интеграла получим t                                                         ”      i--p — "г+а+"+m-Y-1

J( t - T ) m - ^{Y - 1} ( T - 4 ) "^{- 1} E^p„( Я ( т - 4 ) " ) d T = Г ( m - Y ) X    1 ^Я_Г/t ^{4 )}---------

?                    ’                       pZAP ) ^r ( " i + "  + m - у )

ξ                                                        i = p

Тогда

t

J m -^Y y, ( f )( t ) = j ( t - 4 ) ■ -^{Y 1} E p , ( Я ( t - 4 ) " ) f ( 4 ) d 4 .

Далее, m-1

d—j ^{m -Y} f ( t ) = dt m - 1        p

rm -1 t       ^ \ i i - p/, " i +i + " + m -у -1

dn^V ( 4 ) 2 i 1 M^^-4---- dt ^m 0     _z t p ( p ) Г ( " г + a + m - у )

t∞ f i 1 (t - 4)"i+"-у d4. vp J Г("г + a +1 - у)

= j f ( 4 ) 2 X i^p

0        i = p

Математика

И наконец, применяя к последнему выражению оператор Jγ-α после элементарных выкла- док, получим

Значит,

Тогда

t _∞

- JX

0 i = p - 1

m                  t ∞

J ^Y-" d m J m ^-Y y_r ( f )( t ) = J X jp ^{- 1)} dt                      0 j = p - 1

t,    -

D ^aY y p ( f )( t ) = J X ^ - ⁽ p ) 0 _ i = p - 1

t _∞

D ^aYy_p ( f )( t ) — y p - 1 ( f )( t ) = J X

0 i = p - 1

i  ) 2 ^{i - ( p - 1)} ( t - ^ ) ^{a i + a - 1}

(p - 1)     r(ai + a)

j + 1

I

I p )

( t _{- ξ} ) α j + α - 1 Γ ( α j + α )

f ( ξ ) d ξ .

'i + A (t - ^gi+a-1 v p ) r(ai + a)

f ( ξ ) d ξ

i - ( p - 1)         α i + α - 1

i +1| ^ t. ^).-----f (^)d§ —

^ p )    r(ai + a)

t _∞

-f ( ^ ) ^ = 4 x 0 1 = p <  p

( i ) Г ^p ( t - ^ ) ^{a i + a - 1}

Γ(αi + α)

f ( ξ ) d ξ = λ f p ( t )

Таким образом,

Dα,γyp(f)(t)-yp-1(f)(t)=λyp(f)(t), то есть при всех значениях p = 1, 2,... выполняются равенства

( D ^{α , γ} - λ ) y p ( f )( t ) = y p - 1 ( f )( t ).

Теорема доказана.