Новая порядковая структура действительных симметричных (2*2)-матриц

Теория пространств с сильной порядковой единицей, построенная Е. М. Альфсеном и Ф. В. Шульцем [1], близка к теории операторных алгебр. Эрмитовы части C ^∗ -, W ^∗ -алгебр, а также йордановых банаховых алгебр являются примерами пространств с порядковой единицей.

Если K — компактное выпуклое множество в некотором локально выпуклом пространстве, то A b (K) — пространство всех ограниченных аффинных функций также является пространством с порядковой единицей.

Классификационная теория пространств с порядковой единицей хорошо развита [2], однако не построены примеры пространств типа I n (n > 2), отличных от выше перечисленных алгебр. В настоящей работе построена операторная реализация пространств с порядковой единицей типа I 2 .

Как известно, собственные значения оператора определенного в конечномерном гильбертовом пространстве играют очень важную роль. Так, например, имеют место утверждения:

• 1)    если все собственные значения действительны, то оператор самосопряжен;

• 2)    если все собственные значения положительны, то оператор положителен (этот факт эквивалентен понятию положительной определенности оператора) ;

• 3)    если все собственные значения самосопряженного оператора лежат в множестве { — 1; 1 } , то оператор является унитарным;

• 4)    если все собственные значения положительного оператора лежат в множестве { 0; 1 } , то оператор является проектором;

• 5)    порядковая норма и норма оператора совпадают и равны модулю наибольшего собственного значения оператора.

Все эти понятия согласованы с алгебраической структурой B(H ) — алгебры ограниченных операторов в конечномерном гильбертовом пространстве H . Например, произведение двух положительных, коммутирующих элементов — положительный элемент.

В пространстве с порядковой единицей нет, вообще говоря, операции умножения.

Пусть p >  1. Введем следующие определения.

Определение 1. Для T = ^ a b ^

G M 2 ( R ) sa определим следующие числа:

A i = 2 (a + c + ( | 2b | ^p + | a —

c | ^p ) ^p) ,   A 2 = 2 (a + c — ( | 2b | ^p + | a — c | ^p ) ^p)

и назовем их p-собственными значениями матрицы T .

При p = 2 эти числа совпадают с обычными собственными значениями матрицы T :

^ 1’2 = 2 (a + c ± P | 2b | 2 + | a

-

c | ² .

Определение 2. Матрицу T = деленной, если A i,2 >  0, т. е.

ab bc ^∈

M 2 ( R ) sa назовем p-положительно опре-

I

a + a +

c + (|2b|p c — (|2b|p

+ | a

+ | a

-

-

c | ^p ) ¹ >  0, c | ^p ) ¹ >  0.

В этом случае будем писать T >p

θ, где θ — нулевая матрица.

Если T — p-положительно определенная матрица, то легко показать, что a >  0 и c >  0.

При p = 2, в силу (2) имеем a + c >  0 и (a + c) ² >  (2b) 2 + (a — c) ² . Отсюда ac > b² . Это означает, что T >  0 в обычном смысле.

т               f 4 1 \

Пример 1. Пусть T = I 12 ) и p >  1. Находим p-собственные значения Ai^:

11   11

4 + 2 + 2 • 2 p =6 + 2 • 2 p > 0, 4 + 2 — 2 • 2 p =6 — 2 • 2 p > 0.

Значит, T — p-положительно определенная матрица.

Пример 2. Матрица

T =

2 3 + 1

2 3 —

p-положительно определенная для всех p >  3, но неположительно определенная в обычном смысле.

Заметим, что произвольная положительно определенная матрица будет p-положительно определенной для всех p >  2. Это вытекает из известного неравенства: (a ² +b ² ) 2 >  (a ^p + b p ) ^p для всех p >  2 и a,b G R ⁺ .

Через M _p ⁺ обозначим множество p-положительно определенных матриц.

Лемма 1 . M + является конусом в пространстве M 2 ( R ) _sa .

CПустьT=(a b)”S=( т. е. имеем

a 1

b 1

b 1

c 1

— p -положительно определенные матрицы,

I

a + c +( | 2b | ^p a + c — ( | 2b | ^p

+ | a

+ | а

-

-

c | ^p ) ^p >  0, c | ^p ) ^p >  0

и

I

a 1 + c 1 + ( | 2 b 1 | ^p + | a 1 a 1 + c 1 — ( | 2 b 1 | ^p + | a 1

-

-

c i | ^p ) p >  0, c i | ^p ) ^p >  0.

Нужно установить соотношения

T + S >p 9; AT >p 9 при A >  0; M _p ⁺ П ( — M _p ⁺ ) = { 0 } .

Так как T + S =

/ a + a _i V b + b l

b + b i c + c i

, то мы должны доказать, что имеют место нера-

венства a + ai + c + ci + (|2(b + bi) |p + |a + ai — c — ci |p)p > 0,

a + a i + c + c i — (1 2(b + b i ) | p + | a + a i — c — c i | p ) p >  0.

Первое неравенство очевидно, так как все слагаемые положительны в силу условий леммы. Второе равносильно неравенству a + ai + c + ci > (|2(b + bi)|p + |a + ai — c — ci|p)p .

Из положительности T и S имеем a + ai + c + ci > (|2b|p + |a — c|p) 1 + (|2bi|p + |ai — ci|p)p .

В силу неравенства Минковского, выполнено

( | 2(b + b i ) | p + | a — c + a i — c i | p ) p 6 ( | 2b | p + | a — c | p ) p + ( | 2b i | p + | a i — c i | p ) 1 .

Из двух последних неравенств вытекает T + S >p 6.

Если А >  0, то очевидно, что AT >p 6.

Пусть M + П ( — M p ) = { 6 } . Тогда для ненулевого элемента T этого множества неравенства T >p 6 и — T >p 6 выполняются одновременно. Из них имеем, что a + c >  0 и a + c 6 0, т. е. a + c = 0, а также | 2b | p + | a — c | p = 0, из которого следует, что 2b = 0 и a — c = 0. Следовательно, a = b = c = 0, т. е. T = 6. B

Как обычно, с помощью конуса M p+ определяется порядок в M 2 ( R ) _sa , который назовем p-порядком : T > _p S, если T — S > _р 6.

Определение 3. Проективной единицей (аналог проектора) назовем p-положительно определенную матрицу, если все ее p-собственные значения лежат в множестве { 0; 1 } .

Это определение согласовано с теорией пространств с порядковой единицей [1].

Лемма 2. Проективными единицами в M2(R)sa являются единичная матрица E, нулевая матрица θ и матрицы, имеющие вид и = 1Г + t it\ )’                        (3)

2 t 1—t где числа t и t0 удовлетворяют условию |t|p + |t0|р = 1.

ab bc

<1 Пусть p-собственные значения матрицы U = лежат в множестве {0; 1}.

Если предположить, что A i = А 2 , то из определений 1 и 2 имеем A i = 1, А 2 = 0, т. е.

2 (a + c + ( | 2b | ^p + | a — c | ^p ) ^p ) = 1 и

- (a + c — ( | 2b | ^p + | a — c | ^p )?) = 0.

Отсюда вытекает, что a + c = 1, |2b|p + |a — c|p = 1.

Введем следующие обозначения: a — c = t, 2b = t ⁰ . Тогда имеем, что | t | ^p + | t ⁰ | ^p = 1 и a = 2 (1 + t), c = 2 (1 — t), b = 2 1 ⁰ . Следовательно, U имеет вид (3).

Если Ai = A2 = 1, то из (1) вытекает a + c — 2, a — c — 0,  2b — 0, т. е. a = 1, c = 1, b = 0. Значит, U = E. Если Ai = А2 = 0, то имеем a + c = 0, a — c = 0, 2b = 0.

Отсюда a = 0, c = 0, b = 0. Значит, U = 0. B

Очевидно, что если U — проективная единица, то матрица

U 0 = E — U = 2( - t

- t ⁰

1 + t

)

также будет проективной единицей.

Множество проективных единиц в M 2 ( R ) sa обозначим через P .

Лемма 3 . Множество P является ортомодулярной решеткой с нулем θ и единицей E, т. е. логикой относительно p-порядка и ортодополнения (4) .

C Очевидно. B

Все элементы P , отличные от θ и E , являются атомами (минимальными элементами) логики P . Оказывается, что любую матрицу T Е M 2 ( R ) sa можно разложить по атомам.

Лемма 4 . Для каждой симметричной матрицы T существуют атомы U T , U _T ⁰ и числа α, β такие, что имеет место разложение:

T = aUT + eUTr •                              (5)

C t и t0

Предположим, что для симметричной матрицы T =

ab bc

существуют

с условием | t | p + | t ⁰ | p = 1, определяющие Ut , UT , и числа а, в такие, что

числа имеет

место разложение (5). Подставляя данные в (5) и переходя к поэлементным равенствам,

приходим к системе a + в = a + c,

< (a — в )t = a — c, (a — в )t 0 = 2b.

Можно считать, что sgn t = sgn(a — c) и sgn t ⁰ = sgn(2b). В противном случае (t, t ⁰ ) заменим на ( — t, — t ⁰ ) (это приведет лишь к тому, что Ut и U^ поменяются местами).

Если k = | (a — в) -1 | , то из последних двух равенств системы (6) выводим t = k(a — c), t ⁰ = k(2b) для некоторого положительного числа k. Так как | t | p + | t ⁰ | p = 1, то k p ( | 2b | + | a - c | ^p ) = 1, и находим

( | 2b | + | a — c | p ) p

Тем самым можно найти t и t ⁰ , а из первых двух уравнений системы (6) выразить α и β :

a - c                    2 b

1 ,                                                          1 ;

(|2b| + |a — c|p) p            (|2b| + |a — c|p) p a = - (a + c + (|2b|p + |a — c|p)P

в = 2 (a + c — ( | 2b | ^p + | a — c | ^p ) ^p ) . B

Из полученного разложения T вытекает следующая лемма.

Лемма 5 . Конус Mp является порождающим в пространстве M 2 ( R ) _sa , т. е. M 2 ( R ) sa = M p - M p

Разложение (5) показывает естественность введения определения 2, так как в определении p-порядка требуется положительность коэффициентов в (5), которое можно рассматривать как «спектральное разложение» матрицы. Эти коэффициенты и есть p-собственные значения матрицы.

Пространства M 2 ( R ) _sa с новым p-порядком обозначим через Mp ( R ) _sa .

Лемма 6. Отображение T → kT kp, определенное равенством kTkp    2 (|a + c| + (|2b|p + |a — c|p)p) ,                              (7)

является нормой в Mp( R ) _sa .

C 1. Если k T k _p = 0, то a + c = 0, 2b = 0 и a — c = 0. Следовательно, a = b = c = 0, т. е. T = 0.

• 2.    k AT ||_p = | A | k T ||_p для любого A G R — очевидно.

• 3.    Пусть ^T =( ab) и S =( £

  — произвольные матрицы. Тогда

  
  

k T + S k p = | a + a i + c + c i | + ( | 2(b + b i ) | ^p + | a + a i — c — c 1 | ^p ) ^p

• 6 | a + c | + | a i + c i | + ( | 2b | ^p + | a — c | ^p ) ^p + ( | 2b i | + | a i — c i | ^p ) ^p = k T k p + ||S k p . B

Нетрудно заметить, что если T G Mp ( R ) _sa имеет разложение T = aUr + виТ , то k T k p = max {| a | , | в |} .

В силу единственности разложения (5) можно определить модуль матрицы T :

| T | = 2 | a + c + ( | 2b | ^p + | a — c | ^p ) ^p | Ut + | a + c — ( | 2b | ^p + | a — c | ^p ) ¹ | U_T .        (8)

Как обычно, с помощью следа матрицы определяется L ₁ -норма в M_p( R ) _sa .

Лемма 7 . Отображение T → k T k 1 , определенное равенством

||T k i = tr( | T | ) = 2 ( | a + c + ( | 2b | ^p + | a — c | ^p ) 1 | + | a + c — ( | 2b | ^p + | a — c | ^p ) ^p | )

= max | | a + c | , ( | 2b | ^p + | a — c | ^p ) 1 j , (9)

является нормой в M _p ² ( R ) sa .

• C Доказательство аналогично доказательству леммы 6. B

Нетрудно заметить, что если T G Mp ( R ) _sa имеет разложение T = aUr + вЦр, то k T k i = | a | + | в | .

Напомним некоторые понятия из теории пространств с порядковой единицей [1, 3].

Определение 4. Порядковой единицей в упорядоченном векторном пространстве A называется такой положительный элемент e , что для любого a ∈ A , - λe 6 a 6 λe , при некотором A > 0.

Определение 5. Пространством с порядковой единицей называется упорядоченное нормированное пространство с порядковой единицей e, порядок на котором архимедов (= (Vn G N) na 6 e ^ a 6 0) и норма определяется по формуле kak = inf {A > 0 : —Ae 6 a 6 Ae}.

Эту норму называют порядковой нормой.

Определение 6. Норму, определенную в M p 2 ( R ) _sa с помощью p-порядка, назовем p-порядковой нормой.

Несложной проверкой доказывается следующая

Лемма 8 . Единичная матрица E будет p-порядковой единицей в M p 2 ( R ) _sa и норма, определенная в лемме 6, совпадает с p -порядковой нормой.

Пусть p и q — такие числа, что p + q = 1. Через M q ( R ) _sa обозначим пространство M 2 ( R ) sa с q-порядком.

Теорема 1. Пространства (MpR).^, , || • ||_p) c p-порядковой нормой и (Мц^^, , || • ||i) c L 1 -нормой находятся в отделимой, порядковой и нормированной двойственности относительно линейной формы h T, S i = tr(TS) .

• <1 Пусть

T =( a by S =( a¹ $ h M 2 (Ru

Тогда tr(TS) = aa 1 + 2bb 1 + cc 1 .

Если h T,S i = tr(TS ) = 0 для всех S , то при a = a i , b = b i , c = c i имеем, что a ² + 2b ² + c ² = 0, значит, T = 0.

Проверим, что если для T Е Mp2(R)sa верно hT,S) > 0 при всех S Е Mq, то T >p 0. Сначала рассмотрим случай проективных единиц. Пусть тт _ 1 ( 1 + t t0 А р                 1 С 1 + s s р

U =2^  t0   1 - t ) Е Mp(R)sa,  V =2^ s0   1 - s ) Е Mq (R)sa’ где \t\p + \t0\p = 1, |s|q + \s0\q = 1. Тогда tr(UV) = ^ £(1 + t)(1 + s) + 2t's0 + (1 — t)(1 — s)] = 2 (1 + ts + t's0)-        (10)

В силу неравенства \ ts + t ⁰ s ⁰ \ 6 ( \ t \ ^p + \ t ⁰ \ ^p )( \ s \ q + \ s ⁰ | q ) = 1, имеем, что 1+ ts + t ⁰ s ⁰ >  0. Значит, tr(UV) >  0.

Так как произвольный элемент S Е M²( R ) _sa имеет разложение S = 6Vs + yVS и S >_q 0 лишь в том случае, когда 6 >  0 и y >  0, то достаточно проверить выполнение неравенства tr(TS) >  0 для всех проективных единиц S = V Е M²( R ) _sa .

Пусть T Е M p2 ( R ) _sa имеет разложение T = aUT + ви Т . Тогда T > _p 0 равносильно a >  0, в >  0.

Предположим tr(TV) = a tr(U _T V) + в tr(U T V) >  0 для любой проективной единицы V Е M²( R ) _sa . Это означает

2a(1 + ts + t ⁰ s ⁰ ) + 2в(1 — ts — ts ⁰ ) >  0.                      (11)

В силу произвольности V можно считать s = |tt P и s ⁰ = |t 00P в (11) и имеем, что a >  0.

Аналогично, полагая s = —\t\^p /t и s ⁰ = —| t ⁰ l^p /t ⁰ имеем, что в >  0.

Точно таким же путем доказывается, что будет выполнено условие: для любого S ∈ M, 2 ( R ) _sa из h T, S i >  0, T Е M, + , вытекает S > _q 0.

Теперь докажем, что имеют место утверждения:

\h T,S i\ 6 | T | p | S | i ,   T Е Mp 2 (R)sa,  S Е Mq(R)s,;

k T k p = sup {|( T,S )| : ( V S E Mq(R)sa) k S k i 6 1};

k S k i = sup © |h T,S i| : ( V T E M _p ² ( R ) sa ) k T k p 6 1}.

Из (10) вытекает, что 0 6 h U, V i 6 1 для всех проективных единиц U E Mp(R) _sa и V E M²( R ) sa .

Пусть T E M²( R ) _sa и T = aUr + виТ — его разложение. Тогда k T k p = max {| a | , | в |} , по определению. В силу вышесказанного, в равенстве |( T, V i| = | a h U r , V i + в h UT , V il можно выбрать V E M²( R ) _sa так, чтобы в правой части остался max {| a | , | в |} .

Пусть теперь T E M²( R ) _sa , S E M²( R ) _sa — произвольные и T = aU + ви 0 , S = 5V + yV ⁰ . Тогда

|h T, S i| = | a^U, V i + aY h U, V 0 i + e^U 0 , V i + eY h U 0 , V 0 i|

= ^ | ab(1 + ts + t s ) + aY(1 — ts — t s ) + в^(1 — ts — t s ) + eY(1 + ts + t s ) |

6 2( | a^ | (1 + ts + t ⁰ s ⁰ ) + | aY | (1 — ts — t ⁰ s ⁰ ) + | eY | (1 — ts — t ⁰ s ⁰ ) + | eY | (1 + ts + t ⁰ s ⁰ ))

6 2 max {| a | , | в |} [ | ^ | (1 + ts + t ⁰ s ⁰ ) + | y | (1 — ts — t ⁰ s ⁰ ) + | 5 | (1 — ts — t ⁰ s ⁰ )

^{+ |} Y ^{| (1+ ts +} t ⁰ s ^{0 )}] =^{max {| a |} , ^{| e |} ( |} 5 | ⁺ | Y | ) = k ^T k p k ^S k i . B

Как сказано выше, из того, что логика P атомична и ее единичный элемент E есть сумма только двух ортогональных U и U ⁰ следует, что пространство с порядковой единицей M²( R ) _sa имеет тип I ₂ [2]. Так как разложение (5) есть ортогональное разложение матрицы T , то пространства M _p ² ( R ) _sa и M _q ² ( R ) _sa находятся в спектральной двойственности [3].

Итак, доказана следующая

Теорема 2. Пространство Mp ( R ) _sa является спектральным пространством с порядковой единицей типа I ₂ относительно р-порядка.

Так как разложение (5) в M²( R ) _sa ортогонально, т. е. является «спектральным разложением», то можно определить любую степень матрицы, возводя в эту степень, коэффициенты разложения. Например, рассмотрим «квадрат»:

/ у \ (2)                                                       2

T ⁽²⁾ = ( a Ь) =4 (a- + c + ( | 2b | ^p + | a — c | ^p )^p) U r

1 /                        Y 2

+ 4 (a + c — ( | 2b | ^p + | a — c | ^p ) p) UT .

Подставляя в эту формулу значения Ur и UT = E — Ur из леммы 4 после некоторых выкладок имеем

_T (2) = 2 [

4 У

3a ² + 2ac — c ² + ( | 2b | ^p + | a — c | ^p ) ^p        4b(a + c)

4b(a + c)         — a ² + 2ac + 3c ² + ( | 2b | ^p + | a — c | ^p ) ^p

.

Этот «квадрат» действительно есть обобщение обычного квадрата, так как при р = 2 T ⁽²⁾ = T ² , т. е. новый «квадрат» совпадает с квадратом в обычном смысле при р = 2.

Насколько разные эти квадраты для р = 2, показывает следующий факт.

Известно [4], что пространство M ₂ ( R ) _sa с помощью обычного квадрата превращается в JB-алгебру, так как верно равенство (C * -свойство нормы): k T ² k = k T ||² (T E M ₂ ( R ) _sa ). Здесь k · k — операторная норма матрицы.

Это равенство не имеет место для p-порядковой нормы, а именно, существуют элементы T £ M²(R) _sa , для которых k T ² ||_р = k T k p.

Непосредственным вычислением можно показать, что равенство H T ² k p = k T k p (T £ M p² ( R ) _s a ) равносильно следующему

( | 2b | ^p + | a - c | ^p ) ^p = ( | 2b | ² + | a - c | ² ) ²

для всех a, b, c £ R , которое верно только при p = 2. Это означает, что M²( R ) _sa нельзя превратить в JB-алгебру при p = 2.

Но надо отметить, что и в этом случае (с новым «квадратом») верно соответствующее равенство:

k T ⁽²⁾ k p = k T k p , T £ M p² ( R ) sa .

Из этого следует, что p-порядковая структура M p2 ( R ) _sa очень близка к алгебраической структуре M 2 ( R ) sa .

Например, имеет место, следующее простое

Утверждение 1. Матрица T £ M²( R ) _sa является проективной единицей тогда и только тогда, когда T ¹² = T.

C Легко проверить, что U ⁽²⁾ = U для всех проективных единиц. Пусть T ⁽²⁾ = T .В силу (12) это означает, что

3a ² + 2ac - c ² + ( | 2b | ^p + | a - c | ^p ) ^p = 4a, b(a + c) = b,

- a ² + 2ac + 3c ² + ( | 2b | ^p + | a - c | ^p ) ² = 4c.

Из второго уравнения имеем a + c = 1. Учитывая это и сложив два остальных, имеем ( | 2b | ^p + | a - c | ^p ) ^p = 1. B

Аналогичными рассуждениями, как и при доказательстве леммы 2, получим, что T — проективная единица.

Определение 4. Симметричную матрицу назовем симметрией (или самосопряженной унитарной матрицей), если все ее p-собственные значения лежат в множестве ^{{- 1; 1 }} .

Лемма 9 . Симметриями в M²( R ) _sa являются единичная матрица E, - E и матрицы, имеющиe вид

^S = (t o - t),                                  -³

где числа t и t ⁰ удовлетворяют условию | t | ^p + | t ⁰ | ^p = 1 .

C Доказательство аналогично доказательству леммы 2. B

Нетрудно проверяется, что S ⁽²⁾ = E для всех симметрий S .

Пространство с порядковой единицей M p2 ( R ) _sa обладает свойством «положительного квадратного корня»:

Для каждой p-положительно определенной матрицы T £ M p2 ( R ) _sa существует p-положительно определенная матрица S £ Mp ( R ) _sa такая, что S ⁽²⁾ = T.

Этот «квадратный корень» обозначим через S = (2V T . Таким образом мы получаем более простую формулу для определения модуля матрицы, чем в (9):

| T | = ( p/T ?²) , T £ Mp 2 ( R ) sa .

Теорема 3. Пусть T — p -положительно определенная матрица и λ 1 , λ 2 — ее p -собственные значения. Тогда ее квадратный корень вычисляется по формуле

(w = 1

к

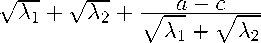
2b

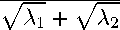
<1 Предположим,

xy yz

такая, что

стему уравнений:

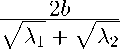
V a 1 + V a 2

-

\

(a — c)

T a1 + Va2 /

что существует p-положительно определенная матрица S =

S (2) = T . Тогда x + z >  0 и, в силу (12), имеем следующую си-

3x ² + 2xz — z ² + ( | 2y | ^p + | x — z | ^p ) ² = 4a,

< y(x + z) = b,

_— x ² + 2xz + 3z ² + ( | 2y | ^p + | x — z | ^p ) ^p = 4c.

Решая эту систему получим требуемое. B