Новая теория тяготения, осцилляции звезд и 11-летний цикл активности Солнца

• A.    Введение

В работах [1, 2, 3, 4, 5, 6] была предложена новая теория электромагнитных и гравитационных полей, основанная на принципе материальности физического трехмерного пространства в форме трехмерной гиперповерхности V ³ в объемлющем четырехмерном евклидовом пространстве W 4 . Материальные объекты, такие как элементарные частицы, в этой теории связываются с геометрическими и топологическими структурами. В частности, электрический заряд связывается с экстремумами функции высоты гиперповерхности V 3 , вложенной в W ⁴ , а величина электрического заряда представляется целым числом, равным эйлеровой характеристике специальным образом выделенных на V ³ областей с границей. Частицы с барионным зарядом в этой теории представляются топологическими ручками типа ручек Уилера, а сам барионный заряд оказывается равным числу ручек Уилера, “вклеенных” в область пространства, соответствующую данной частице. Поля в данной теории ассоциируются с полями маркеров частиц гиперповерхности V ³ (лагранжевыми переменными), а исходные уравнения, которым они удовлетворяют, появляются в теории в виде тождеств, которым удовлетворяют некоторые комбинации маркерных полей и их производных.

Необходимость в создании новой теории полей и частиц, которая бы включала в себя все основные теории современной физики в обновленном виде, такие, как теория тяготения, электромагнетизм и квантовая теория, обсуждалась в работах [3, 5, 6]. В кратком изложении основное требование к новой теории сводится к первому принципу материальности:

Принцип 1. Любой объект физической теории, наделенный измеримыми физическими свойствами, должен являться материальным объектом.

В противоположность этому пространство-время и Специальной (СТО) и Общей (ОТО) теорий относительности, являются нематериальными объектами, но при этом наделяются физическими свойствами, способными влиять на движение материальных тел в экспериментах. Например, в ОТО пространство-время наделяется свойством кривизны, которое, фактически, определяет свойства поля тяготения. В новой теории все поля и свойства частиц связываются с маркерными полями (лагранжевыми переменными), что гарантирует их материальность.

Применение данной новой теории в упрощенном виде для описания строения и динамики звезд ( в частности, звездных осцилляций) было изложено в работах [7, 8, 9, 10]. В этих работах на основе использования маркерных полей и их связи с полем тяготения была построена теория динамического равновесия звезд и других астрофизических объектов. В частности, была предложена модель автомодельных осцилляций звезд, в том числе модель осцилляций Солнца, объясняющая 11-летние колебания солнечной активности.

В данной работе обсуждается общая идеология использования новой теории тяготения в задачах описания динамического равновесия звезд и их автомодельных осцилляций. Приводятся уточняющие модель соотношения, касающиеся структуры зонального потока, а также теплового режима в звездах, которые сказываются на осцилляциях светимости звезд, а также диаграммы период-светимость.

• B.    Маркерные тождества и поле тяготения в классической физике

Основным общим положением новой теории является постулат, что трехмерное физическое пространство является гладкой гиперповерхностью V ³ общего вида, вложенной в евклидово пространство четырех измерений W 4 . Описание геометрии такой гиперповерхности в каждый момент времени 力 строится с помощью одного уравнения:

u =尸(x,力)， где 尸(x, t) - функция высоты, x = (x1, т2, x3) - декартовы координаты на выделенной в W4 трехмерной гиперплоскости Р3, играющей роль системы отсчета, и u - ортогональная декартова координата к Р3 в W4 (см. рис. 1). Таким образом, нематериальное евклидово пространство W4 вместе с вложенной в него гладкой гиперповерхностью V3 представляет базовый уровень материальности. Следующий уровень материальности - это геометрические и топологические структуры V3 как гиперповерхности.

Описание материальных объектов опирается на второй принцип материальности:

Принцип 2 . Любое физически измеримое свойство материальных объектов должно выражаться через свойства маркерных полей (лагранжевых переменных) £ ° ( 丁,之,± ) , а = 1 , 2 , 3, связанных с материальными точками этого объекта, которые по определению удовлетворяют уравнению переноса:

де ^а     де ^а     де ^а      де ^а

+ "击 + 。再 + %

三建 + (V, V ) е ^а = 0,

Q = 1,2, 3.

(B.1)

Здесь и далее везде будем использовать правило суммирования по повторяющемуся индексу.

Поскольку гиперповерхность V3 является материальным объектом, то сама функция высоты 尸(x, t) как величина, характеризующая физические свойства, также выражается через маркерные поля еа. В каждой области V3 е V3, ограниченной изоповерхностью 尸(x, t), должно выполняться соотношение:

尸=Jo + ；|e|2, |e|2 = (e1)2 + (e2)2 + (e3)2, где e = (e1, e2, e3) - радиус-вектор в пространстве маркеров, £ = +1 в случае, если в точке с |e|2 = 0 尸 достигает максимума и £ = —1 - если минимума. J0 - значение 尸 в точке |e|2 = 0 (см. [1, 2, 4, 6]).

• B.1.    Плотность массы

Система (B.1) допускает дифференциальное тождество, которое можно записать в следующем виде:

"+ д^ ( ”丿 | ) ⁺ ^ (加丿 | ) ⁺ ^ ( W | ) 三丿 卜 + ^{div( v |} J | )=^{0 ,}            ( В.2 )

где функция | J | - якобиан преобразования от координат z,r в координаты e 1 ,e ² пространства значений маркеров:

| J | = | det J | .                                                    (B.3)

Здесь

J

号 ^e 1

学 ^e 2

33 ^e y ^e z

(B.4)

Уравнение (B.2) является стандартным уравнением теории маркеров в лагранжевом подходе в классической гидродинамике и представляет собой уравнение сохранения числа частиц. Как и в классической гидродинамике любая функция:

夕 = 〃 o M (e 1 ,e ² ,e ³ ) | J | , (B.5)

где 从 (e ¹ , e ² , e ³ ) - произвольная безразмерная дифференцируемая функция маркеров, может быть отождествлена с плотностью массы вещества, поскольку она автоматически удовлетворяет закону сохранения массы:

p _t + div( u p) = 0. (B.6)

Здесь и далее масштабный коэффициент М 。 имеет размерность массы. В этом случае (B.2) эквивалентно уравнению неразрывности. Физический смысл безразмерной функции 从 ( e ) состоит в том, что она определяет относительную массивность каждой отдельной точки среды, связанной с маркерами e = (e ¹ , e ² , e ³ ). Величина | J | представляет собой плотность маркеров, т.е. плотность числа точек гиперповерхности V ³ в окрестности точки с координатами х .

В рассматриваемой теории p - это плотность массы материи, из которой состоит сама гиперповерхность V 3 . Вещество, которое является предметом описания классической физики и квантовой теории и которая фигурирует в качестве материи в СТО и ОТО, является геометрическими и топологическими элементами структуры V 3 . Например, как уже упоминалось, частицы с барионным зарядом связываются с областями V 3 , содержащими топологические ручки Уилера (см. [2, 4, 6]). Обоснование такой связи и общие принципы описания электрического заряда и строения частиц с помощью топологии V ³ содержатся в работах [2, 4, 6].

• B.2.    Уравнение Пуассона и маркеры

Описание гравитационных и электромагнитных полей, параметры которых в силу второго принципа материальности должны выражаться через функции e ° ( x ,t), а = 1,2, 3, строится на основе двух дифференциальных тождеств, первое из которых имеет вид дифференциального закона Кулона для точечного заряда в маркерных переменных:

а второе имеет следующий вид:

de    de¹   de ²    de ³

=+4= 3.

乙 de ^a   de ¹    de ²    de ³

а =1

(B.8)

Переходя в этих тождествах к физическим координатам x , получаем форму этих тождеств, которую можно использовать для отождествления с электрическим полем и полем тяготения. В физических координатах тождеству (B.7) можно придать такой вид

div D = 4тт | J | 8( e ),

(B.9)

где поле

P ，=丄 e 。竺

“    | e | ³ de 。

(B.10)

отождествляется с фундаментальным полем электрической индукции. Тождество же (B.8) представляется в форме:

div g = 4^G P ( e )p,

(B.11)

где G - постоянная тяготения Ньютона, а поле с компонентами:

47r                8т, ⁷

g ⁷ = ₁3- G ^ ( e ) | J | e 。— + ^otW] ⁷

(B.12)

отождествляется с полем напряженности поля тяготения с точностью до некоторого поля, дивергенция от которого равна нулю. Функция P ( e ) имеет следующий вид:

Р

1 + - e 。

d ln 从 de 。

(B.13)

Эта функция является атрибутом поля тяготения в случае, если массивность 从 ( e ) точек V ³ меняется от точки к точке и может рассматриваться как параметр “скрытой” массы, поскольку в уравнение Пуассона (B.11) входит в виде множителя вместе с постоянной тяготения G. Поэтому G _eff = G P ( e ) можно рассматривать как эффективную “постоянную” тяготения. С другой стороны, оставляя постоянную тяготения неизменной, можно функцию 夕 eff = 夕 Р = 夕 + p D рассматривать как эффективную плотность материи, а величину p D как плотность скрытой массы или темной материи.

Далее в данной статье все внимание будет обращено на поле тяготения и не будем касаться вопросов, связанных с фундаментальным электромагнитным полем. Описание этого поля и его свойств можно найти в [1, 2, 4, 6]. Нас же будет интересовать поле g и его связь с динамикой астрофизических объектов в классическом приближении.

• C.    Переход к непрерывной среде классической механики

Для описания процессов, протекающих на масштабах астрофизических объектов, таких, как звезды, не относящиеся сейчас к релятивистским объектам (нейтронные звезды, черные дыры и т.п.), достаточно использовать законы классической механики. Поэтому теория фундаментальных полей, кратко изложенная в предыдущем разделе, должна быть редуцирована, чтобы ее выводы привести в соответствие с основными положениями классической механики.

Процедура приведения общей схемы новой теории к классической сводится к двум шагам. Первый состоит в отождествлении трехмерной гиперплоскости Р3 е W4 с плоским пространством классической механики. Второй шаг - это отождествление топологических структур, например, ручек Уилера, соответствующих барионам, с точками непрерывной среды, заполняющей пространство. Аналогичное отождествление возможно и для других частиц, например, электронов. Последнее можно сделать в силу малости размеров топологических структур типа ручек Уилера и других элементарных частиц по сравнению с расстояниями классической теории. Таким образом мы получаем мир классической механики. Переход к уравнениям Ньютона и уравнениям квантовой теории описан в работах [1, 2, 4, 6]. Наиболее существенным дополнением, которое остается в классической механике после такого перехода, - это описание поля тяготения с помощью маркерных полей, которое является универсальным как для новой теории, так и для классической.

Последним не “классическим” элементом редуцируемой теории является наличие в ней изменяющейся в пространстве функции 从 ( e ) массивности частиц среды. Эта функция не связана ни с представлением о неевклидовом пространстве в форме гиперповерхности V ³ е W 4 , ни с топологическими свойствами частиц. Вообще говоря, эта функция должна быть элементом классической теории тяготения для непрерывных самогравитирующих сред, которые представляют собой смесь частиц различной массы. Однако в классической механике эта функция не используется, хотя в большинстве астрофизических объектов присутствуют химические элементы с различным массовым числом. Эта же функция должна была бы появиться в теории строения и эволюции галактик и космологии, поскольку в моделях этих теорий в качестве элементов среды выступают сами звезды. Поскольку звезды существенно различаются по массам, то эффекты скрытой массы, связанные с изменениями 从 ( e ) в пространстве, должны иметь существенное значение, что, по всей видимости, обнаруживается в эксперименте в форме темной материи. В настоящей работе эти важные аспекты динамики различных астрофизических объектов не будут обсуждаться, поскольку в качестве примера того, как работает редуцированная теория тяготения, будет описана модель осцилляций звезд типа Солнца. Для звезд типа Солнца изменчивость 从 ( e ) в пространстве не играет существенной роли, поскольку такие звезды в основном состоят из водорода с относительно небольшой примесью гелия. Поэтому далее в данной работе мы будем полагать 从 ( e ) = 1, что соответствует Р = 0. Покажем как такой подход приводит к новым выводам в рамках классической механики, в том числе, позволяет описать 11-летний цикл солнечной активности.

C.1. Уравнения динамики самогравитирующего газа

Рассмотрим движение самогравитирующего газа как непрерывной среды вблизи области с повышенной плотностью массы. Будем полагать, что система обладает цилиндрической симметрией, так, что все параметры среды не зависят от азимутального угла. В такой области имеется центр, в котором плотность достигает своего максимума и убывает некоторым образом при удалении от этого центра. В этот максимум поместим начало цилиндрической системы координат. Будем предполагать, что поток газа имеет зональную составляющую с осью вращения, совпадающей с осью N цилиндрической системы координат. В этом случае уравнения движения газа и уравнения гравитационного поля можно записать в такой форме:

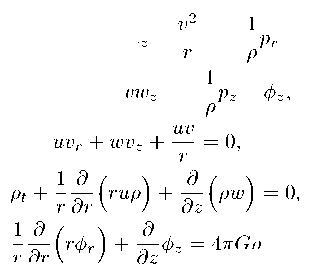
丁

- 0 之

P

+ uu _r + wv _z + — = 0

丁

4?rGp,

仅 于 + UW _r + 仅仅 N

(C.1)

(C.2)

(C.3)

К этой системе необходимо добавить уравнение состояния, которое близко к уравнению идеального газа:

∘ p = — pT.

∘

Здесь А - универсальная газовая постоянная, 4 g - молярная масса газа, T - абсолютная температура. Полагая, что процесс переноса плазмы в звездах является глобально адиабатическим, т.е. энтропия не меняется вдоль линий тока, приходим (см. Приложение 1 и [9]) к следующему общему уравнению состояния:

p = Ke ^s/c - р ⁷ ,

(C.5)

где 6 - энтропия, c _v - молярная теплоемкость при постоянном объеме и 7 - показатель адиабаты. Параметр К связан с состоянием газа при какой-то выделенной температуре.

C.2. Динамика маркеров, плотность вещества и уравнение состояния

При наличии цилиндрической симметрии для описания полей достаточно двух маркерных полей e ^a ( r, z, t ) , q = 1, 2, которые теперь принимают следующий вид:

де ^а     де ^а      де ^а

(C.6)

(C.7)

at      дг       az — ‘    — ‘ .

Уравнение сохранения числа частиц будет иметь такой вид:

曙 + дГ (〃|J\) + Ž (刨 J О =0, где функция | J| - якобиан преобразования от координат z,r в координаты е1, е2 пространства значений маркеров, аналогичная (B.3), но с матрицей:

J

^е 1

^е г

'N 2

'N

е-

е:

(C.8)

Соответственно, плотность массы в общем случае будет выглядеть так :

P = M o M ( e )\ J | /r,

(C.9)

где 从 ( e ) - массивность частиц среды, которая теперь может быть связана с массовым числом ядер атомов среды в случае неоднородного химического состава газа, М о - масштабный коэффициент, имеющий размерность массы. В этом случае (C.7) эквивалентно уравнению неразрывности (C.2) в цилиндрической системе координат. Как было указано выше, в данной работе далее будем полагать 从 ( e ) = 1.

Полагая, что тепловые процессы в звезде являются квази-адиабатическими, для функции плотности энтропии 6 имеем соотношение 6 = S( e ) + 6 0 (t), где S( e ) - часть энтропии, переносимая без изменений вдоль линий тока, зависящая только от маркеров, а 6 ° (t) - часть энтропии, изменяющаяся глобально со временем. В результате уравнение состояния можно записать в таком виде:

P = К S ( е )ст(і)р ⁷ ,

(C.10)

где S = exp(S( e )/c _v ) и a(t) = exp б 。« )/%. Теперь для абсолютной температуры имеем следующее выражение:

T = K 0 a ( t ) S ( e )p7T.

(C.11)

C.3. Уравнение Пуассона для самогравитирующего газа

Уравнение Пуассона в цилиндрической системе координат теперь появляется из формального тождества:

^ ²^ де ^а    де ¹ де ²

2^ деа   де1 + де2    , а=1

которое приводит к такому уравнению для | J | :

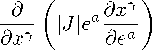
2 | j | .

(C.13)

Введем векторное поле K с компонентами:

К ⁷

士仗, b =1

T =1, ^{2 ,}

(C.14)

Как и в [9], компоненты напряженности поля тяготения д & , а = 1,2 можно представить в виде:

-勿 Т 9 1 == - 2^ 0 1 j | К 1 - 1%,

- 0 z Т   = - ^1^ 0 | J | К ² + ； 必 ,                    (C.15)

Отсюда находим, что компоненты напряженности гравитационного поля тождественно удовлетворяют уравнению Пуассона:

( C9 i ) + ^-( 9 2 )= 4 ^Gp.                               (C.16)

丁 or       oz

• D.    Параметры среды и потока в автомодельных переменных

Гидродинамический поток в моделях статического равновесия звезд отсутствует. В теории динамического равновесия поток существует и состоит из радиального потока с компонентами:

и = H ("r = а £, w = F ("z = b&

(D.1)

и зонального со скоростью з = v ( r, z,^ ) . В случае выбора радиального потока в форме (D.1), что аналогично закону Хаббла в космологии, маркерные функции е ^а = e ^a ( r, z, 力) являются произвольными функциями двух автомодельных переменных :

€ = r/а ⑴， С = z/6 ⑴，                                ( D.2)

т.е.:

e ^a = £ ^a (€,C) а =1,2.

Функции а = а« ) и b = b« ) называются масштабными факторами, а функции:

- параметрами Хаббла. Из (D.1) следует:

где:

а _

H = -, F а

b b

(D.3)

du   du   du    du

=后 + u^T + w才=а€, d力   也    dr    dz dw dw dw dw / =丽+ "丽+w3l =k

(D.4)

Плотность среды в автомодельные переменных будет иметь такой вид:

Mo   ° p =-⑴2 b⑴厶(€,С'

U (€< ) |       det 纭纪

8   ，，       戈受

(D.5)

(D.6)

∘

Функцию R (£<) в дальнейшем будем называть коэффициентом плотности. Из этого следует:

I J | K 1 = ： (u 嘗 т² 11 ) = ； Q ( g'C ，

I лк ² = - ：( £ ¹ ^ - 唄 ) = :d ( g ， c ・

Функции /С і и 心 удовлетворяют в силу (C.16) уравнению:

gd^ ⁽d + д^ 心=胃外

(D.7)

(D.8)

Используя теперь соотношения (C.10) и (C.11), получаем следующее представление для давления и абсолютной температуры:

о 7                                                о 7 ^{- 1}

Р = М 7 KS (g ， Q 。⑴ a ^{- 2 7} 6 ^{- 7} R , Т = М 7 K 0 。⑴$ ( e )e ^{- 2 ( 7 - 1)} & — ^{7 +1} R = П ⑴丁 ( e ) ，    ( D.9)

где:

о 7 — 1

丁 (g ， C= S (g ， Q R 怎 0 ， П&) = Ко ₍ 7(і)М₍ 7 ^{- 1} _а ^{- 2} ( ^{7 - 1)} ₆ ^{- 7 +1} .

Функцию Т = Т (£，《) будем называть коэффициентом температуры.

В терминах маркерных полей e ^a ( r, z ， 力) выражается и зональная компонента скорости потока.

Третье уравнение системы (C.1) в такой форме:

d d д

(丽+"而+他不)£ = 0

где £ = п ( г, z ， t ) r - удельная плотность момента импульса среды. Отсюда следует, что функция £ (〃 z ， 力) является функцией маркеров £ = £ ( е ¹ ， е ² ) и следовательно :

£("

(D.10)

r

Это соотношение позволяет замкнуть описание динамики газа в терминах маркерных полей.

• E.    Коэффициент энтропии

Одним из важных элементов модели, изложенной в [9], является появление в уравнениях модели пространственного распределения плотности и температуры коэффициента энтропии S ( g ， 《) . Обычно при моделировании структуры и эволюции звезд для замыкания уравнений динамики их дополняют уравнением выделения энергии ядерным источником в центральной области звезд. Однако область выделения занимает относительно малый объем звезды, а во всех остальных ее слоях происходит перенос тепла и излучения с помощью различного рода механизмов. Дополнительное уравнение энерговыделения в силу сделанных предположений будет сводиться к уравнению для функции S ( g ， С ) для заданных коэффициентов непрозрачности вещества звезды и функции энерговыделения. Обе последние функции обычно выражаются через степенные функции температуры и плотности среды и носят, как правило, модельный характер, поскольку все коэффициенты этих функций установить с помощью лабораторных исследований невозможно. Поэтому в их записи остаются всегда не до конца точно известные параметры, которые устанавливаются с помощью подгонки под реальные наблюдательные данные. В силу этого в работе [9] был предложен другой подход для определения функции S ( g ， С ) .

Вместо того, чтобы решать уравнение энерговыделения для отыскания функции S ( e ) , которое все равно требует определенной подгонки, в работе [9] было предложено сразу представить S ( e )

∘

как функцию плотности среды R или температуры Т . В этой работе предлагалось представлять функцию S ( g ， С ) в следующем виде:

о °

S = Я о R ，

(E.1)

где параметр 8 подгонялся под определенные характеристики распределения температуры и плотности в пространстве. Такой подход подробно описан в [9].

Результатом такого подхода является то, что вследствие квази-адиабатичности процессов в условиях динамического равновесия и при учете потоков тепла в звезде, формулы для давления и температуры (D.9), принимают форму эффективных адиабат с показателем Т е// = 7 + 8. Фактически это означает, что потоки тепла оставляют процесс адиабатическим и только меняют его показатель. Этот факт может играть очень важную роль в строении звезд, поскольку при определенных условиях может приводить к потере устойчивости звезды при нестандартных условиях. Как было показано в [9] подгонка параметра 8 для Солнца приводит к такому наилучшему значению 8, при котором 7 е// — 6/5 при 7 = 5/3. Следует отметить, что значение 7 = 6/5 выделено в теории Лейна-Эмдена тем, что плотность и температура нигде не обращаются в ноль.

Таким образом, использование (E.1) или иной более общей модели такого типа приводит с одной стороны к упрощению процедур подгонки результатов моделирования, а с другой указывает на возможные существенные изменения во взглядах на условия устойчивости звезд, особенно вместе с общей идеей динамического, а не статического их равновесия.

• F.    Уравнения в автомодельных переменных

Полученные соотношения, описывающие параметры среды и потока в автомодельных переменных, позволяют теперь записать уравнения динамики в этих же переменных. Следуя работе [9], будем полагать далее b = 。 ( 力 ).Это упрощение необходимо для возможности разделить переменные в уравнениях динамики в автомодельных переменных. В этом случае уравнения динамики принимают такой вид:

&g -

一四^Ž(s 方7) - *(心 + 2)， q3£3       Q 忘然、 /     @2         £  ，

叫 ^ ( s 月 ⁷ ) - 丁 C) R

(F.1)

Для разделения переменных теперь необходимо потребовать выполнения следующих условий:

£ ² =仆)，

田=出 0 亿， 0 + a ^-1 ⑴ N ( g ， Q.

(F.2)

где 九 ( £，《 ),W o (£ ， C) и N( £，《 )-некоторые вспомогательные функции, требующие уточнения. Для функции П«), которая содержит одну произвольную пока функцию о«), более общим требованием, чем в [9], для возможности разделения переменных является формальное представление:

0 = 。1 ⑴ + 02 ⑴/a⑴，n = nі(^) + n2«)， nі =k001上)й7-%-3(7-1)，

П 2 = K o 0 2 ⑴ Ч ^{7 -}%-* ^{7 - 1} ) ^{- 1} ，

(F.3)

где функции о і«) и 0 2«) определяются из условия разделения переменных. Потребуем выполнения следующих условий для функций Пі«) и П2«):

а Пі ⑴ 2ttGM o @ ² П2 ⑴ 2ttGM o

К °№ 2 。 1 ⑴ a ^{4 - 3 7} = Q = const;

4 万 G

К°№ 2 0 2 ⑴ a ^{3 - 3 7} = Q 2 = const;

4 万 G

(F.4)

П

”0 ( Q i + 2 )

2 冗 GQ i 4 o

-a2

(1+*).

Из последнего соотношения следует, что отношение 。 丁 = Q 2 /Q 1 имеет размерность длины. В результате подстановки соотношений (F.2) и (F.4) в (F.1) приходим к уравнениям для пространственного распределения зонального потока:

学) - 2^^GM 0 (!t^+j ^ е 頁 ⁷ )) = 〃&

2nGM° ( 1    -         云 7 )) =“ •

(F.5)

и для распределения плотности среды вместе с компонентами вектора /С ] и 心 :

Л € + Q 1 友( S 月 ⁷ ) + 心一； Ф о ,с = 0 ,

(F.6)

Л 《 +

Q 1   ( S 頁 ⁷ ) + 心 + j % ， g = 0.

Уравнение эволюции в этом случае будет иметь такой вид:

a ² &  — - = 2^GM ₀ A, Q

(F.7)

в точности совпадающее с аналогичным уравнением из работы [9]. Важным является то обстоятельство, что уравнение автомодельной эволюции со временем остается неизменным по отношению к работе [9]. Это означает, что все основные выводы, сделанные в [9], остаются в силе и после уточнений модели в данной работе.

G. Пространственное распределение плотности и параметров зонального потока

Комбинируя уравнения (F.6) и (F.5), а затем исключая из уравнений для зонального потока перекрестным дифференцированием функцию N, получаем уравнение для функции 九 ：

1 д %&с     Г1 д (j д / о ⁷ Л d /1 д / о ⁷ Л!

j 沃飞「- " 2 [j 灰灰 Ox )丿+氏 ^^R )丿] = ^3- ,

где " 2 = 2 冗 GM 0 Q 2 .

Аналогично, исключая из уравнений (F.6) функцию W°, приходим к модифицированному ∘ уравнению Лейна - Эмдена для функции 冗：

∘

》 + x +

Q1 [ 1 Midj (sx⁷)) +1 ( 41 (sx⁷))] =0.         ( G.2 )

X             X

Параметр A = 3Л/2 называется (см. [9]) параметром динамического равновесия . Отличием этого уравнения от аналогичного уравнения в работе [9] является наличие множителя Р . Как уже отмечалось, эта функция фактически произвольна и определяется начальным распределением массивности частиц в пространстве в момент перехода звезды в режим автомодельных осцилляций. Кроме этого, при медленном изменении химического состава звезды за счет ядерных реакций эта функция также должна медленно меняться.

Комбинируя уравнения (G.1) и (G.2), в результате получаем уравнение для 九 ( £,《 ) ：

1 д_ (丄、_ jdj=

3— — 7 ( A+ X ),

(G.3)

где для сокращения записи введено обозначение:

7 = 4 冗 GM 0 Q 2 /Q 1 = 4^GM o a _T .

(G.4)

Уравнение (G.3) обобщает аналогичное соотношение в работе [9]. Интегрируя это уравнение

(G.3), получаем следующее обобщенное выражение для 九 ( £,《 ) ：

Һ =()-》 7 卜 4 - 7€ 2 / R g 恋 + M& 先 2 ,                (G.5)

где 历(《 )-постоянная интегрирования по g, зависящая произвольным образом от 《 .Последнее соотношение эквивалентно распределению зональной скорости следующего вида:

0 = Q — 1 4 = а — 1 У (g,C,

(G.6)

где

V =

\

(-2~ - "В ^g 2 - )/ R ^g " ^g + 历(&方).

(G.7)

∘                          ∘∘        ∘

Исходя из условия ограниченности R на оси вращения и полагая lim R=R o ( 《 ),где R o ( 《 )- х— 0

некоторые ограниченные функции переменной 《 ,находим, что при b o ( 《 ) 三 0, локальная угловая скорость потока ® = va - 1 /g на оси вращения будет иметь конечное значение:

з。 © = !吧3 = !吧总 q-2 lim

(^ - ")) - )^{g -}2 / R 3^g = a ^-2 ⑴ j (3^ ^- ")) ― )Rо © • 0

Введение функции R o ( 《 )обусловлено тем, что граничное условие R (0) = 1 в чистом виде имеет место только в сферическом приближении (см. [9]). В общем же случае плотность может меняться на оси вращения в зависимости от 《 ,оставаясь ограниченной величиной. Из последнего соотношения следует, что в данной работе решается проблема бесконечной угловой скорости вращения на оси N в обновленном варианте разделения переменных, которая имелась в работе [9]. Вместе с тем, в плоскости экватора при 《 =0 соотношение (G.5) переходит в точности в соотношение для Һ из работы [9]:

九=~2^ g4 + Һо.

Из (G.7) получаем следующее выражение:

Һо = h(go, 0) = (3^ - Л7^ g4 -)g0 / R gdg •(G.9)

Параметр h o , согласно [9], является важным параметром для оценок периода осцилляций Солнца. Поскольку соотношение (G.8) не изменяется по сравнению с работой [9], то все дальнейшие выкладки и оценки из этой работ остаются в силе. Также неизменным по сравнению с аналогичным уравнением в [9] остается уравнение (G.2). Поэтому анализ пространственного распределения плотности, приведенный в [9], не требует дополнительного анализа здесь.

Отметим лишь некоторые, наиболее важные элементы этой новой модели строения звезд, которые изменяют некоторые установившиеся в этой теории представления.

• H.    Параметр динамического равновесия

Уравнение (G.2) можно рассматривать как обобщенное уравнение Лейна-Эмдена (LEm), хорошо известное в астрофизике, как уравнение звездных политроп [11, 12]. Существенным отличием

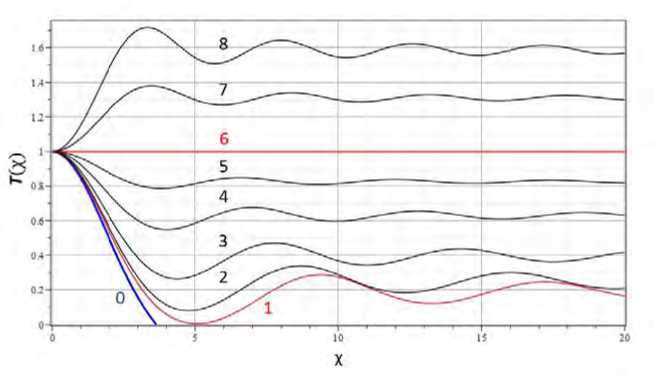
Рис. 1. Зависимости Т = Т ( х ): 0 - А = 0, 1 - А = - 0 . 0851, 2- А = - 0 . 125, 3 - А = - 0 . 25, 4 - А = - 0 . 5, 5 - А = - 0 . 75, 6 - А = - 1, , 7- А = - 1 . 5, 7- А = - 2 . 0

(G.2) от уравнения LEm является наличие ненулевого параметра А, который в [9] был назван параметром динамического равновесия. Роль этого параметра в рассматриваемой теории строения звезд крайне важна, поскольку решает проблему отрицательных или мнимых значений плотности массы в теории звездных политроп. Эту проблему иллюстрируют графики на рис. 1. На этих графиках приведены кривые распределения температуры в звездах с показателем политропы п = 3/2 (одноатомный газ 7 = 5/3) и однородным показателем энтропии S (£<) = 1 для различных значений параметра динамического равновесия А. График температуры представлен в приближении радиальной симметрии относительно радиальной координаты х = ， £ ² + С 2 . Из представленного графика видно, что кривая с А = 0 (синяя кривая с номером 0), что соответствует классическому уравнению LEm [11, 12], пересекает ось абсцисс в некоторой точке х о , после которой решение становится комплексным. Это означает, что такая модель становится совершенно нефизичной при X > Х о . Обычно значение х о отождествляется с радиусом звезды, область не физических значений просто игнорируется. Поэтому считается, что обращение в ноль плотности на некотром расстоянии от центра звезды плотности, является хорошим граничным условием, хотя и не совсем точным. В большинстве простых моделей, но более общих, чем модель Лейна-Эмдена, заранее считается, что плотность должна обращаться в ноль на некотором расстоянии от центра звезды. Это расстояние признается радиусом звезды. За пределами этого радиуса строится другая модель, описывающая, по возможности, фотосферу и корону звезд.

В отличие от этого, остальные кривые на рис. (1) с А < 0 демонстрируют другое поведение. Как было показано в [9], начиная с некоторого критического значения параметра динамического равновесия А, равного для п = 3/2 значению А t - 0.851 (красная кривая под номером 1), кривые вообще не пересекают ось абсцисс так, что температура и плотность всюду остаются положительными и ограниченными функциями. Последнее указывает на то, что такие модели имеют физический смысл на всем расстоянии от центра звезды. Более того, появление максимума температуры (и плотности), следующего за ее первым минимумом, который надо рассматривать как реальный радиус звезды (минимум температуры в фотосфере), указывает на естественное объяснение известного максимума температуры в короне Солнца.

Следует отметить, что при втором критическом значении А = -1.0 решение с граничным условием Т(0) = 1 при всех показателях политропы п при S = 1 одно и то же Т = 1. Это напоминает космологические решения, для которых плотность остается всюду постоянной. При этом поведение масштабного фактора будет описываться уравнением, близким к уравнению для масштабного фактора в космологии Фридмана [13]. Уравнение для масштабного фактора в мо- дели Фридмана не содержит слагаемого, связанного с зональным потоком или,другими словами, вращения структуры вокруг оси г.

Кривые со значениями А < — 1 (кривые с номерами 7 и 8) имеют минимум в центре структуры. По сути такие структуры можно рассматривать как модели войдов [14]. Такие структуры могут появляться и быть достаточно устойчивыми за счет радиального потока Хаббла из их центра и наличия зонального потока. Такие структуры могут появляться после взрыва массивных звезд или других объектов.

Из этого анализа следует, что введение параметра динамического равновесия в теорию звездных политроп решает целый ряд проблем и делает эти модели гораздо более жизнеспособными, чем считалось ранее.

• I.    Модель 11-летних осцилляций Солнца

Работоспособность предложенной модели была доказана в работе [9], где было показано, что звезды с параметрами Солнца из стандартной модели последнего, вытекает период осцилляций близкий к наблюдаемому 11-летнему циклу солнечной активности. Этот результат является прямым следствием того, что рассматриваемые модели строятся на основе представления компонент поля тяготения с помощью поля маркеров (B.12) и общей идеи динамического равновесия звезд, а не строго статического. Именно эти идеи и приводят к уравнению для масштабного фактора (F.7), которое имеет при определенных условиях замкнутые фазовые траектории, которые и описывают осцилляции звезд. Сами соотношения (B.12) и (C.15) являются следствием связи между материальной структурой пространства, как гиперповерхности V ³ е W 4 , но могут интерпретироваться в рамках классической механики как формальные соотношения, позволяющие специальным образом представить компоненты поля тяготения.

Чтобы дать общее представление о модели осцилляций звезд в динамическом равновесии, кратко опишем основную схему исследований, в результате которых в [9] было дано объяснение 11-летнему циклу солнечных осцилляций. Анализ осцилляций звезд сводится к анализу уравнения (F.7) для заданных параметров звезды. Как и в работе [9] уравнение (F.7) приведем к виду динамической системы в безразмерной форме:

|| = Т-3 +sign(" ),-2, £ = у,(I.1)

Здесь:

T = 。/。 0 , у = 方 0 C/a 0 , 丁 = 〃方 0 ,

Постоянные а о и 力 о определяются следующим образом: где

4^GMo—

〃 =---о А, Q0 =从/|〃 |, 力 о =

Динамическая система (I.1) имеет интеграл движения:

у- + sign。) - + 与=E,

• 2           т

который аналогичен интегралу энергии частицы, совершающей одномерное движение в потенциальном поле сил.

Для моделей с ^ < 0 (А < 0) все траектории динамической системы (I.1) для — 0.5 < E < 0 являются замкнутыми, а траектории c E > 0 асимптотически стремятся к точкам (т = а , у = 土 2EE ) при t т ±а (см. Рис.1 c). Из (I.3) следует, что фазовые траектории для — 0.5 < E < 0 пересекают ось абсцисс при значениях безразмерной координаты, равной:

.

(I.4)

T =

±   1 ± V2E +1

Параметр	Значение
Радиус R q	7 • 10 8 [см]
Экваториальная скорость 。 ①	2 • 10 5 [см/с]
Показатель адиабаты 7	5/3 (Одноатомный газ)
Плотность в центре р ө	150 [г/см 3 ]
Температура в центре T q	- 15 • 10 6 [K]

Таблица 1. Основные параметры Солнца.

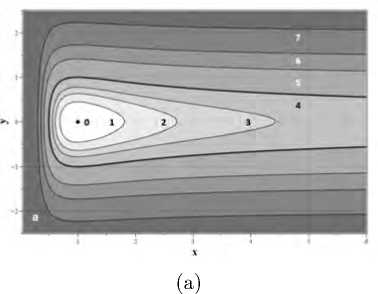
Рис. 2. Фазовые траектории динамической системы (I.1) (a) для 0 - Е = - 0 . 5, 1 - Е = - 0 . 4, 2 - Е = - 0 . 3, 3 - Е = - 0 . 2, 4 - Е = 0 . 0, 5 - Е = 0 . 5, 6 - Е = 1 . 0, 7 - Е = 2 . 0; (b) для начальных значений ( с (0) = 0 . 9 , д (0) = 0) и ( с (0) = 0 . 6 ,д (0) = 0)

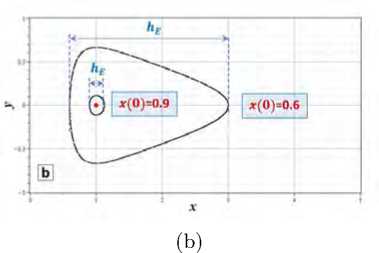
Точка > соответствует максимальному сжатию структуры, а точка х - - максимальному расширению. Размах колебаний 九 石 = | х — - х + 1 в случае осцилляций определяется следующим образом:

九 石 = | х — — х + |

71 —ЭД 闵

(I.5)

Для Е = 0 х - = а , а при Е > 0 эта точка лежит в отрицательной области значений х - < 0, но траектории в полуплоскости х < 0 не имеют физического смысла.

Период колебаний Р е газодинамического объекта, соответствующий определенному значению параметра Е, вычисляется в соответствии со следующей формулой:

X -

^Р Е = ²/

xdx          7Т ， 2

(I.6)

- 2Ех ² + 2хF — 2 | Е | з / 2 ^х +

Как следует из этого соотношения при Е т 0 период колебаний стремится к бесконечности.

Типичные фазовые траектории системы (I.1) представлены на рис. (2).

В работе [9] приведена методика определения параметров модели, исходя из набора основных параметров звезды. В качестве таких параметров взяты следующие параметры: радиус звезды А * , плотность в центре звезды р * = р(0), температура в центре звезды 7 * , скорость зонального потока на экваторе звезды 。 * и показатель политропы 7. Для Солнца эти параметры приведены в Таб. 1.

Дополнительным подгоночным параметром модели, кроме параметра 8 в (E.1), был параметр 九 о , а точнее параметр £ :

е = 1 — %x0 / ( uq& ) ² ・

Эти параметры связаны со скоростью зонального потока. Параметры в этом соотношении определены в Таб. 1 и Таб. 2. На графиках на рис. 3(a,b) приведены зависимости периода осцилляций и

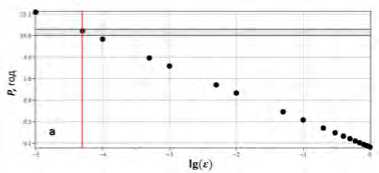
(a)

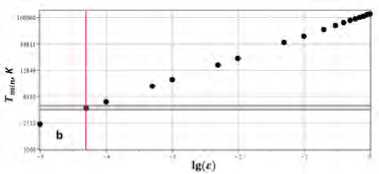
(b)

Рис. 3. Зависимость периода осцилляций Р ( Е ) (a) и T min (b) от з

температуры в фотосфере от параметра £. Фактически, подгонка по параметру £ не является по сути подгонкой, поскольку, определяет сразу два параметра модели. Следовательно выбор одного из них автоматически должен приводить к выбору второго. Из графиков (3) следует, что период осцилляций примерно 11 лет соответствует наблюдаемой реально в фотосфере Солнца температуре примерно 4500K ° . Что указывает на реальную работоспособность данной модели.

Как показано в работе [9] наилучшей моделью для Солнца является модель со следующими значениями параметров модели, которые были получены с помощью численных расчетов:

Параметр	Значение
Показатель энтропии 8	-- 7/15
Эффективный показатель адиабаты 7 ’ (с учетом потока тепла)	- 6/5
Р ( Е * )	— 11.03 [год]
工	-- 7.788 • 10 - 12
Х 0	- 13537
X i	- 132000
V min	- 6 • 10 - 3
T min — 1Tmiп Т ®	- 4500 [K]
Tm.ax	- 0.00717
T m.ax = V maq ^ ®	- 101000 [K]
£	- 6 • 10 - 5

Таб. 2. Параметры наилучшей модели для Солнца

∘

Распределение коэффициентов температуры Т , плотности R и энтропии S , соответствующие наилучшей модели, представлены на рис. 4(a,b,c).

Таким образом, модель, основанная на приведении новой теории тяготения к условиям классической физики тяготения дает хорошее согласие с экспериментальными данными в отношении осцилляции звезд типа Солнца. Можно предполагать, что она пригодна для описния и звезд других классов, например, цефеид, хотя для подтверждения такого вывода необходимы дополнительные исследования.

J. Диаграмма период-светимость

Одним из способов доказательства того, что данная модель пригодна для описания переменных звезд, в том числе и цефеид, может являться сравнение вычисляемой в рамках модели аналитической диаграммы период-светимость с реальными данными. В работе [9] было показано, что диаграмма период-светимость, соответствующая соотношению (I.6) и (D.9) при условии Q 2 = 0

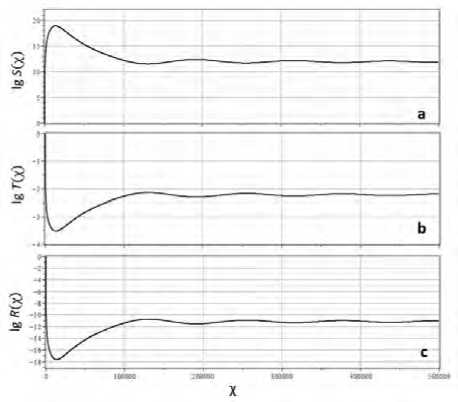
Рис. 4. Распределение параметров среды для наилучшей модели. (A) Коэффициенты энтропии lg( S ) (a), температуры lg( T ) (b) и плотности lg ( R ) (c)

имеет вид:

Здесь L _max

- светимость

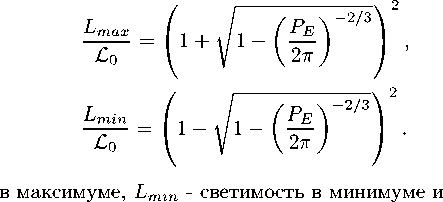
£ о = 4s ( ⁴ 丁 GM ；() - 1 ) J a -² 丁 4 (x0).

(J.1)

(J.2)

Постоянная £ ° является масштабным множителем, содержащим неизвестный изначально параметр о 。 , который можно определить из реальных наблюдений 丄 但 ax и L _min . Следует отметить, что предложенная модель осцилляций не опирается на классический подход, который был предложен в работах [15, 16, 17], и который связывал осцилляции звезд с ионизацией верхних слоев звезды, содержащих гелий. Исходя из основных идей подхода, основанного на новой теории тяготения, осцилляции, аналогичные солнечным с той или иной амплитудой, но при других параметрах должны возникать в звездах любых типов, в том числе и массивных звездах на поздних стадиях эволюции.

В данной работе по аналогии с [9] можно показать, что в случае Q 2 = 0 формула для диаграммы период-светимость имеет более общую форму:

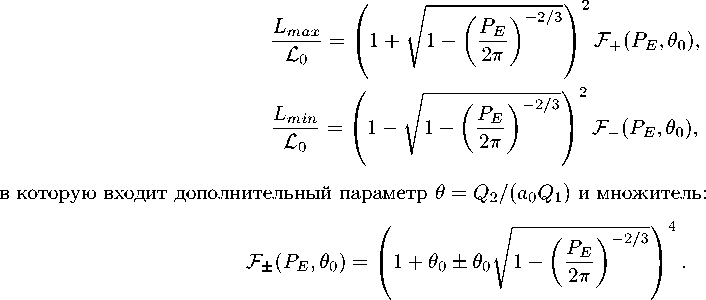
(J.3)

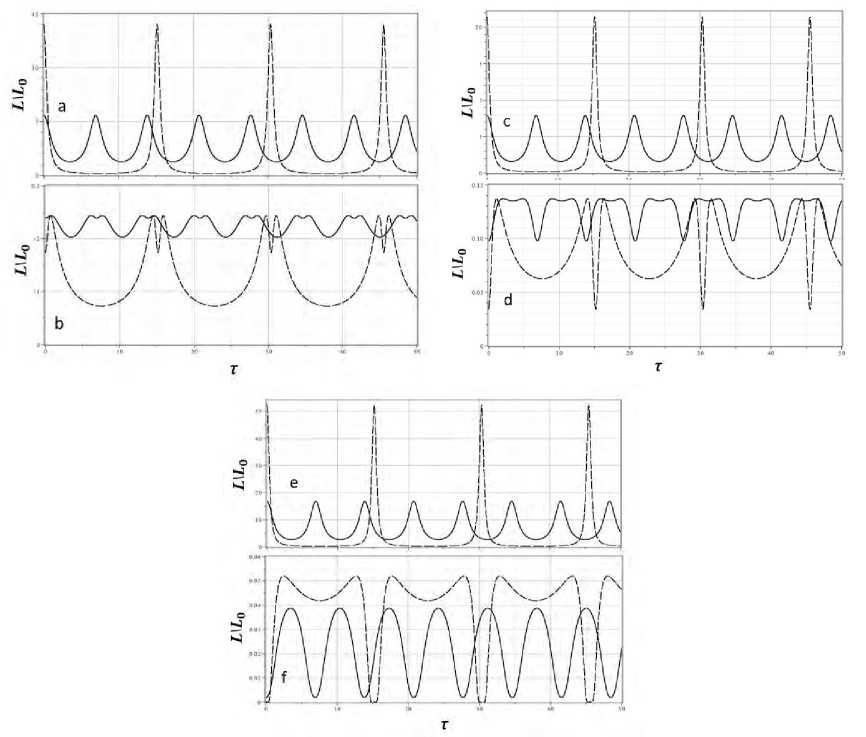
Рис. 5. Изменения относительной светимости для фазовых траекторий на рис. 2b: (a) Ө о = 0 . 3, (b) Ө о = - 0 . 3, (c) Ө о = 0 . 4,(d) Ө о = - 0 . 4,(e) Ө о = 0 . 65, (f) Ө о = - 0 . 65

При этом характер осцилляций светимости переменных звезд, находящихся в динамическом равновесии, усложняется. На рис. 5(a,b,с,d) представлены графики осцилляций относительной светимости (J.2), соответствующие фазовым кривым на рис. 2c (с теми же обозначениями кривых, соответствующих разным начальным условиям) для четырех значений параметра 9 ° , как положительных (5(a,с)), так и отрицательных (5(b,d)).

Как видно из графиков на рис. 5, при отрицательных значениях параметра 9 ° кривые блеска усложняются. Для некоторых типов цефеид в реальности имеются нестандартные детали кривой блеска. Некоторые типичные кривые блеска на примере конкретных цефеид приведены на рис. 6.

Сравнение кривых на рис. 5 и 6 показывает, что для определенного класса цефеид (типа FF-Орла) предлагаемая модель вполне способна описывать кривую блеска, а значит, и диаграмму период-светимость. Для цефеид второго типа (8-Цефея) модель должна быть подстроена под несимметричный характер кривой блеска. Вид кривой блеска на 6b близок к изменениям не радиуса звезды (переменная 十⑴ ) ， с изменениями которого связана оценка светимости (J.3), а с изменениями переменной д (。 , которая описывает скорость изменения радиуса звезды. Т.е. в формулу для светимости необходимо включить некоторые эффекты изменения скорости радиуса (кривая лучевых скоростей) на саму светимость. Это требует дополнительных исследований.

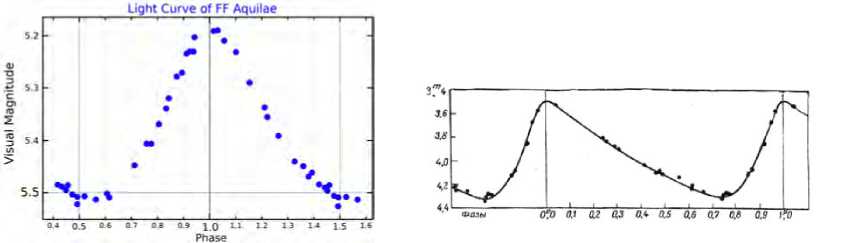
a

b

Рис. 6. Кривые блеска FF-Орла (a) [18] и 6 -Цефея (b) [19]

K. Заключение

Как было показано в данной работе [9], новая теория тяготения при ее редукции к классической для условий структуры звезд дает новые результаты, вполне согласующиеся с реальными данными. В первую очередь это относится к возможности физически адекватно описать плотность и температуру как внутри звезд, так и за их пределами. Это достигается появлением в теории понятия динамического равновесия звезд и других астрофизических объектов. В условиях динамического равновесия звезды могут эволюционировать, но так, что в специальных автомодельных переменных их структура остается неизменной. В уравнениях пространственного строения звезд и их эволюции в рамках данной модели появляется важный параметр - параметр динамического равновесия. Именно наличие этого параметра приводит к новым элементам теории структуры и эволюции звезд, которые согласуются с наблюдениями. Для пространственного распределения этот параметр позволяет строить модели, в которых всюду плотность и температура являются неотрицательными величинами и возникают пространственные дополнительные максимумы и минимумы температуры и плотности, сопоставимые с изменениями этих параметров в короне. В модели эволюции звезд этот параметр является ключевым, поскольку обеспечивает появление фазовых замкнутых траекторий, т.е. нелинейных осцилляций большой амплитуды, в противовес стандартному подходу анализа малых колебаний.

Дополнительные нововедения в работе [9], с одной стороны, позволили упростить анализ модели (например, соотношение (E.1)), а с другой, позволили получить новые элементы описания звезд (например, аналитические соотношения для кривых блеска (J.3) и аналитических диаграмм период-светимость). Все это указывает не только на работоспособность модели осцилляций звезд, но и может служить подтверждением исходных положений новой теории тяготения или, в более общем понимании, теории топологической теории фундаментальных полей [1, 2, 3, 4, 5, 6].