Новые Биядерные арильные соединения сурьмы
Автор: Шарутин В.В.
Журнал: Вестник Южно-Уральского государственного университета. Серия: Химия @vestnik-susu-chemistry
Рубрика: Химия элементоорганических соединений
Статья в выпуске: 1 т.17, 2025 года.
Бесплатный доступ
Методом рентгеноструктурного анализа (РСА) определено строение пяти биядерных арильных соединений сурьмы (Ar3SbX)2O [Ar = 3-FC6H4, X = OC(O)CF2Br (1), Ar = 4-FC6H4, X = OC6H2Br3-2,4,6 ∙ 0,5C8H18 (2), Ar = 4-MeC6H4, X = OC(O)CH2Cl (3), Ar = 4-MeC6H4, X = OC(O)CH2Br (4), Ar = Ph, X = OC(O)C6HF4 (5)], РСА которых проводили на автоматическом четырехкружном дифрактометре D8 Quest Bruker (Мо Kα-излучение, λ = 0,71073 Å, графитовый монохроматор) при 293 К. Кристаллы (1) C40H24O5F10Br2Sb2, M 1177,91; сингония моноклинная, группа симметрии C2/c; параметры ячейки: a = 24,808(9), b = 10,837(3), c = 32,215(10) Å; β = 96,711(19)°, V = 8601(5) Å3; Z = 8; rвыч = 1,819 г/см3; 2q 5,74-68,08 град.; всего отражений 95957; независимых отражений 14384; число уточняемых параметров 532; Rint = 0,0898; GOOF 1,771; R1 = 0,1705, wR2 = 0,4519; остаточная электронная плотность (max/min); 2,34/-4,78 e/Å3], (2) C52H37O3F6Br6Sb2 M 1546,78; сингония триклинная, группа симметрии P-1; параметры ячейки: a = 12,325(5), b = 13,749(6), c = 17,774(8) Å; a = 83,259(16), β = 80,26(3), g = 65,894(15) град., V = 2706(2) Å3, Z = 2; rвыч = 1,898 г/см3; 2q 6,06-59,14 град.; всего отражений 144892; независимых отражений 15098; число уточняемых параметров 623; Rint = 0,0646; GOOF 1,010; R1 = 0,0379, wR2 = 0,0791; остаточная электронная плотность (max/min); 0,92/-1,45 e/Å3], (3) C69H69O7,5Cl3Sb3, M 1489,84; сингония триклинная, группа симметрии P-1; параметры ячейки: a = 10,474(7), b = 11,179(6), c = 29,736(14) Å; a = 88,899(18)°, β = 82,542(19)°, g = 76,22(3)°; V = 3353(3) Å3, Z = 2; rвыч = 1,476 г/см3; 2q 5,56-51,62 град.; всего отражений 65830; независимых отражений 12738; число уточняемых параметров 754; Rint = 0,0510; GOOF 1,037; R1 = 0,0383, wR2 = 0,0803; остаточная электронная плотность (max/min): 0,83/-1,13 e/Å3], (4) C69H69O7,5Br3Sb3, M 1623,22; сингония триклинная, группа симметрии P-1; параметры ячейки: a = 10,585(7), b = 11,255(7), c = 29,712(18) Å; a = 88,41(3)°, β = 82,43(3)°, g = 75,01(3)°; V = 3389(4) Å3, Z = 2; rвыч = 1,591 г/см3; 2q 5,58-33,64 град.; всего отражений 14830; независимых отражений 3789; число уточняемых параметров 754; Rint = 0,0327; GOOF 1,049; R1 = 0,0354, wR2 = 0,0852; остаточная электронная плотность (max/min): 0,76/-0,93 e/Å3], (5) C450H288F72O45Sb18, M 9974,83; сингония триклинная, группа симметрии P-1; параметры ячейки: a = 12,045(12), b = 24,31(3), c = 36,66(4) Å; a = 101,75(5)°, β = 98,50(3)°, g = 98,52(5)°; V = 10216(19) Å3, Z = 1; rвыч = 1,6213 г/см3; 2q 5,6-40,58 град.; всего отражений 99411; независимых отражений 19647; число уточняемых параметров 2519; Rint = 0,0516; GOOF 1,099; R1 = 0,0576, wR2 = 0,1076; остаточная электронная плотность (max/min): 1,78/-1,26 e/Å3].
Строение, биядерный, арильный, соединение, сурьма, рентгеноструктурный анализ
Короткий адрес: https://sciup.org/147248048
IDR: 147248048 | УДК: 546.865 | DOI: 10.14529/chem250108
Текст научной статьи Новые Биядерные арильные соединения сурьмы
К настоящему времени методом рентгеноструктурного анализа установлено строение широкого ряда комплексов сурьмы общей формулы (Ar3SbX)2O (Х = Hlg, NO3, OC(O)R, OR, OSO2R и другие электроотрицательные группы), атомы сурьмы в которых имеют искаженную тригонально-бипирамидальную координацию с мостиковым атомом кислорода и монодентатным лигандом Х в аксиальных положениях, а в экваториальной плоскости располагаются арильные заместители [1–34]. Некоторые молекулы (Ar3SbX)2O являются центросимметричными (центр симметрии – мостиковый атом кислорода), в других – два фрагмента Ar3SbX несколько отличаются друг от друга. Искажение тригонально-бипирамидальной конфигурации молекул проявляется в отклонении валентных углов от теоретических значений и выходе атомов сурьмы из экваториальной плоскости к мостиковому атому кислорода. Расстояния Sb-X в р-оксопроизводных (Ar3SbX)2O значительно меньше аналогичных связей в соединениях общей формулы Ar4SbX и немного больше, чем в соединениях Ar3SbX2. Длины связей между атомами сурьмы и мостиковым атомом кислорода Sb–Oмост меньше суммы ковалентных радиусов атомов сурьмы и кислорода (2,07 Å [35]). Основное различие в геометрии молекул этих соединений заключается в строении фрагмента Sb–O–Sb. В большинстве случаев фрагменты имеют угловую форму и лишь иногда – линейную. Величина угла SbOSb, который изменяется от 130 до 180°, и причины, вызывающие его изменение, являются предметом дискуссии в работах последних лет. В настоящей работе проанализированы основные геометрические параметры неизвестных ранее молекул указанного типа 1–5 (Ar3SbX)2O (Ar = 3-FC6H4, X = OC(O)CF2Br (1), Ar = 4-FC6H4, X = OC6H2Br3-2,4,6 ∙ 0,5C8H18 (2), Ar = 4-MeC6H4, X = OC(O)CH2Cl (3), Ar = 4-MeC6H4, X = OC(O)CH2Br (4), Ar = Ph, X = OC(O)C6HF4 (5).
Экспериментальная часть
В работе использовали органические соединения производства фирмы Alfa Aesar, cоединения 1 - 5 получали по реакции окислительного присоединения, описанной в монографии [4].
РСА кристаллов 1-5 проведен на дифрактометре D8 Quest фирмы Bruker (MoKα-излучение, λ = 0,71073 Å, графитовый монохроматор) при 296(2) К. Сбор, редактирование данных и уточнение параметров элементарной ячейки, а также учет поглощения проведены по программам SMART и SAINT-Plus [36]. Все расчеты по определению и уточнению структуры выполнены по программам SHELXL/PC [37] и OLEX2 [38]. Структуры определены прямым методом и уточнены методом наименьших квадратов в анизотропном приближении для неводородных атомов. Основные кристаллографические данные и результаты уточнения структур 1-5 приведены в табл. 1, основные длины связей и валентные углы - в табл. 2. Полные таблицы координат атомов, длин связей и валентных углов депонированы в Кембриджском банке структурных данных (№ 2233179 (1), № 2183340 (2), № 2233088 (3), № 2233180 (4), № 2217274 (5); ; .
Кристаллографические данные, параметры эксперимента и уточнения структур 1 - 5
Таблица 1
|
Параметр |
1 |
2 |
3 |
4 |
5 |
|
Формула |
C 40 H 24 O 5 F 10 Br 2 Sb 2 |
C 52 H 37 O 3 F 6 Br 6 Sb 2 |
C 69 H 69 O 7,5 Cl 3 Sb 3 |
C 69 H 69 O 7,5 Br 3 Sb 3 |
C 450 H 288 F 72 O 45 Sb 1 8 |
|
М |
1177,91 |
1546,78 |
1489,84 |
1623,22 |
9974,83 |
|
Сингония |
Моноклинная |
Триклинная |
Триклинная |
Триклинная |
Триклинная |
|
Пр. группа |
C 2/ c |
P– 1 |
P –1 |
P –1 |
P –1 |
|
a , Å |
24,808(9) |
12,325(5) |
10,474(7) |
10,585(7) |
12,045(12) |
|
b, Å |
10,837(3) |
13,749(6) |
11,179(6) |
11,255(7) |
24,31(3) |
|
c, Å |
32,215(10) |
17,774(8) |
29,736(14) |
29,712(18) |
36,66(4) |
|
α, град. |
90,00 |
83,259(16) |
88,899(18) |
88,41(3) |
101,75(5) |
|
β, град. |
96,711(19) |
80,26(3) |
82,542(19) |
82,43(3) |
98,50(3) |
|
γ, град. |
90,00 |
65,894(15) |
76,22(3) |
75,01(3) |
98,52(5) |
|
V , Å3 |
8601(5) |
2706(2) |
3353(3) |
3389(4) |
10216(19) |
|
Z |
8 |
2 |
2 |
2 |
1 |
|
ρ (выч.), г/см3 |
1,819 |
1,898 |
1,476 |
1,591 |
1,6213 |
|
–1 µ , мм |
3,199 |
5,489 |
1,370 |
3,006 |
1,269 |
|
F (000) |
4528,0 |
1478,0 |
1494,0 |
1602,0 |
4906,1 |
|
Размер кристалла (мм) |
0,36×0,34×0,18 |
0,29×0,15×0,06 |
0,42×0,2×0,09 |
0,35×0,3×0,1 |
0,31×0,21×0,06 |
|
Область сбора данных по 2 θ , град. |
5,74–68,08 |
6,06–59,14 |
5,56–51,62 |
5,58–33,64 |
5,6–40,58 |
|
Интервалы индексов отражений |
–37 ≤ h ≤ 35, –15 ≤ k ≤ 15, –48 ≤ l ≤ 49 |
–17 ≤ h ≤ 17, –18 ≤ k ≤ 19, –24 ≤ l ≤ 24 |
–12 ≤ h ≤ 12, –13 ≤ k ≤ 13, –36 ≤ l ≤ 36 |
–8 ≤ h ≤ 8, –9 ≤ k ≤ 9, –24 ≤ l ≤ 24 |
–11 ≤ h ≤ 11, –23 ≤ k ≤ 23, –35 ≤ l ≤ 35 |
|
Измерено отражений |
95957 |
144892 |
65830 |
14830 |
99411 |
|
Независимых отражений |
14384 |
15098 |
12738 |
3789 |
19647 |
|
Переменных уточнения |
532 |
623 |
754 |
754 |
2519 |
|
GOOF |
1,771 |
1,010 |
1,037 |
1,049 |
1,099 |
Окончание табл. 1
|
Параметр |
1 |
2 |
3 |
4 |
5 |
|
R -факторы по F 2 > 2 σ ( F 2) |
R 1 = 0,1705, wR 2 = 0,4519 |
R 1 = 0,0379, wR 2 = 0,0791 |
R 1 = 0,0383, wR 2 = 0,0803 |
R 1 = 0,0354, wR 2 = 0,0852 |
R 1 = 0,0576, wR 2 = 0,1076 |
|
R -факторы по всем отражениям |
R 1 = 0,2303, wR 2 = 0,4788 |
R 1 = 0,0681, wR 2 = 0,0888 |
R 1 = 0,0549, wR 2 = 0,0861 |
R 1 = 0,0413, wR 2 = 0,0888 |
R 1 = 0,0925, wR 2 = 0,1310 |
|
Остаточная электронная плотность (min/max), e /Å3 |
2,34/–4,78 |
0,92/–1,45 |
0,83/–1,13 |
0,76/–0,93 |
1,78/–1,26 |
Таблица 2
|
Связь |
d , Å |
Угол |
\ ω, град. |
|
|
1 |
||||
|
Sb1–O3 |
1,979(9) |
O3‒Sb1‒O1 |
177,0(4) |
|
|
Sb1–O1 |
2,208(10) |
O3‒Sb2‒O4 |
179,2(4) |
|
|
Sb1–C21 |
2,096(13) |
C21‒Sb1‒C1 |
116,9(6) |
|
|
Sb1–C11 |
2,087(14) |
C11‒Sb1‒C21 |
112,5(5) |
|
|
Sb1–C1 |
2,121(12) |
C11‒Sb1‒C1 |
129,5(5) |
|
|
Sb2–O3 |
1,939(9) |
O3‒Sb2‒O4 |
179,2(4) |
|
|
Sb2–C31 |
2,111(14) |
C31‒Sb2‒C411 |
120,2(5) |
|
|
Sb2–C411 |
2,129(13) |
C31‒Sb2‒C511 |
113,0(5) |
|
|
Sb2–C511 |
2,122(12) |
C511‒Sb2‒C411 |
125,3(5) |
|
|
Sb2–O4 |
2,197(11) |
Sb2‒O3‒Sb1 |
144,5(5) |
|
|
Преобразования симметрии: 1 +X, - 1+Y, +Z; 2 |
+X, 1+Y, +Z |
|||
|
2 |
||||
|
Sb2–O1 |
1,971(2) |
O1‒Sb2‒O3 |
176,59(10) |
|
|
Sb2–O3 |
2,147(2) |
C31‒Sb2‒C51 |
111,73(13) |
|
|
Sb2–C51 |
2,112(3) |
C31‒Sb2‒C41 |
129,60(13) |
|
|
Sb2–C31 |
2,107(3) |
C41‒Sb2‒C51 |
118,31(14) |
|
|
Sb2–C41 |
2,110(3) |
O1‒Sb1‒O2 |
176,38(9) |
|
|
Sb1–O1 |
1,982(2) |
C11‒Sb1‒C21 |
117,24(13) |
|
|
Sb1–O2 |
2,159(2) |
C11‒Sb1‒C1 |
124,05(13) |
|
|
Sb1–C11 |
2,110(3) |
C21‒Sb1‒C1 |
117,86(13) |
|
|
Sb1–C21 |
2,112(3) |
Sb2‒O1‒Sb1 |
152,12(14) |
|
|
Sb1–C1 |
2,114(3) |
O1‒Sb1‒C11 |
89,30(11) |
|
|
Преобразования симметрии: 1 2 - X, - Y, 1 - Z |
||||
|
3 |
||||
|
Sb2–O1 |
1,993(3) |
O1‒Sb2‒O4 |
178,63(10) |
|
|
Sb2–O4 |
2,176(3) |
C41‒Sb2‒C51 |
120,37(15) |
|
|
Sb2–C41 |
2,103(4) |
C41‒Sb2‒C31 |
125,75(15) |
|
|
Sb2–C51 |
2,113(4) |
C31‒Sb2‒C51 |
112,68(15) |
|
|
Sb2–C31 |
2,108(4) |
O1‒Sb1‒O2 |
177,65(10) |
|
|
Sb1–O1 |
1,971(3) |
C1‒Sb1‒C11 |
123,82(15) |
|
|
Sb1–O2 |
2,193(3) |
C21‒Sb1‒C11 |
120,22(14) |
|
|
Sb1–C11 |
2,123(4) |
C21‒Sb1‒C1 |
115,00(15) |
|
|
Sb1–C1 |
2,114(4) |
O6‒Sb3‒O7 |
174,89(13) |
|
|
Sb1–C21 |
2,114(4) |
C71‒Sb3‒C81 |
115,3(2) |
|
|
Sb3–O6 |
1,9589(9) |
C61‒Sb3‒C81 |
119,2(2) |
|
|
Sb3–O7 |
2,200(5) |
C61‒Sb3‒C71 |
124,7(2) |
|
|
Sb3–C81 |
2,117(5) |
Sb1‒O1‒Sb2 |
139,88(14) |
|
|
Sb3–C71 |
2,115(5) |
Sb3‒O6‒Sb31 |
179,998(2) |
|
|
Sb3–C61 |
2,108(5) |
C68‒O7‒Sb3 |
132,5(6) |
|
|
O6–Sb31 |
1,9589(9) |
C8‒O2‒Sb1 |
125,5(3) |
|
|
Преобразования симметрии: 1 1 - X, 1 - Y, 1 - Z |
||||
Продолжение табл. 2
|
Связь 1 d , Å \ |
Угол 1 ω, град. |
||
|
4 |
|||
|
Sb1–O1 |
1,994(6) |
O1‒Sb1‒O2 |
179,0(3) |
|
Sb1–O2 |
2,184(8) |
C1‒Sb1‒C11 |
124,7(6) |
|
Sb1–C1 |
2,096(11) |
C1‒Sb1‒C21 |
112,9(6) |
|
Sb1–C11 |
2,121(11) |
C11‒Sb1‒C21 |
121,2(6) |
|
Sb1–C21 |
2,127(10) |
O1‒Sb2‒O4 |
178,1(3) |
|
Sb2–O1 |
1,973(6) |
C51‒Sb2‒C31 |
119,2(6) |
|
Sb2–O4 |
2,199(8) |
C51‒Sb2‒C41 |
114,6(6) |
|
Sb2–C51 |
2,096(11) |
C41‒Sb2‒C31 |
125,0(4) |
|
Sb2–C31 |
2,125(11) |
O6‒Sb3‒O7 |
175,2(4) |
|
Sb2–C41 |
2,102(11) |
C71‒Sb3‒C61 |
124,3(9) |
|
Sb3–O6 |
1,9561(13) |
C81‒Sb3‒C61 |
115,7(9) |
|
Sb3–C61 |
2,107(14) |
C81‒Sb3‒C71 |
118,7(8) |
|
Sb3–O7 |
2,259(13) |
Sb2‒O1‒Sb1 |
139,8(3) |
|
Sb3–C71 |
2,086(16) |
Sb31‒O6‒Sb3 |
179,999(1) |
|
Sb3–C81 |
2,070(15) |
O4‒C38‒C39 |
114,1(13) |
|
O6–Sb31 |
1,9560(13) |
O5‒C38‒O4 |
126,9(12) |
|
Преобразования симметрии: 1 1 - X, 2 - Y, 1 - Z |
|||
|
5 |
|||
|
Sb1–O1 |
1,958(7) |
O1‒Sb1‒O2 |
177,6(3) |
|
Sb1–O2 |
2,190(8) |
C11‒Sb1‒C21 |
115,3(6) |
|
Sb1–C11 |
2,106(12) |
C1‒Sb1‒C11 |
128,2(5) |
|
Sb1–C1 |
2,102(11) |
C1‒Sb1‒C21 |
115,4(6) |
|
Sb1–C21 |
2,108(12) |
O1‒Sb2‒O4 |
177,9(3) |
|
Sb2–O1 |
1,983(7) |
C31‒Sb2‒C51 |
115,7(5) |
|
Sb2–O4 |
2,180(8) |
C41‒Sb2‒C51 |
126,2(5) |
|
Sb2–C51 |
2,138(12) |
C41‒Sb2‒C31 |
117,6(5) |
|
Sb2–C31 |
2,092(12) |
O6‒Sb3‒O7 |
176,7(3) |
|
Sb2–C41 |
2,089(13) |
C81‒Sb3‒C101 |
115,9(5) |
|
Sb3–O6 |
1,967(7) |
C91‒Sb3‒C81 |
117,6(5) |
|
Sb3–O7 |
2,178(8) |
C91‒Sb3‒C101 |
125,8(5) |
|
Sb3–C81 |
2,089(11) |
O11‒Sb5‒O12 |
177,2(3) |
|
Sb3–C91 |
2,087(13) |
C181‒Sb5‒C171 |
114,6(5) |
|
Sb3–C101 |
2,126(14) |
C181‒Sb5‒C161 |
126,1(5) |
|
Sb5–O12 |
2,193(7) |
C171‒Sb5‒C161 |
118,3(5) |
|
Sb5–O11 |
1,957(8) |
O6‒Sb4‒O9 |
177,2(3) |
|
Sb5–C181 |
2,102(12) |
C131‒Sb4‒C111 |
113,9(4) |
|
Sb5–O171 |
2,104(12) |
C131‒Sb4‒C121 |
115,6(4) |
|
Sb5–O161 |
2,109(13) |
C111‒Sb4‒C121 |
129,7(5) |
|
Sb4–O6 |
1,984(7) |
O11‒Sb6‒O14 |
177,9(3) |
|
Sb4–O9 |
2,181(7) |
C191‒Sb6‒C211 |
117,1(6) |
|
Sb4–C131 |
2,092(6) |
C201‒Sb6‒C191 |
114,7(6) |
|
Sb4–C111 |
2,104(12) |
C201‒Sb6‒C211 |
127,0(6) |
|
Sb4–C121 |
2,105(11) |
O16‒Sb8‒O19 |
177,6(4) |
|
Sb6–O14 |
2,177(8) |
C281‒Sb8‒C291 |
116,4(6) |
|
Sb6–O11 |
1,985(8) |
C281‒Sb8‒C271 |
124,8(4) |
|
Sb6–C191 |
2,074(7) |
C291‒Sb8‒C271 |
117,9(6) |
|
Sb6–C211 |
2,093(14) |
O16‒Sb7‒O17 |
178,3(4) |
|
Sb6–C201 |
2,047(14) |
C251‒Sb7‒C261 |
115,3(6) |
|
Sb8–O19 |
2,176(8) |
C251‒Sb7‒C241 |
118,2(7) |
|
Sb8–O16 |
1,985(8) |
C261‒Sb7‒C241 |
125,4(6) |
|
Sb8–C281 |
2,063(11) |
O21‒Sb9‒O22 |
175,5(2) |
|
Sb8–C291 |
2,074(12) |
C341‒Sb9‒C331 |
116,3(5) |
|
Sb8–C271 |
2,091(8) |
C341‒Sb9‒C321 |
111,0(8) |
|
Sb7–O17 |
2,178(8) |
C331‒Sb9‒C321 |
132,6(8) |
Окончание табл. 2
|
Связь |
d , Å |
Угол |
ω, град. |
|
Sb7–O16 |
1,937(8) |
O21 - Sb9 - C341 |
91,7(4) |
|
Sb7–C251 |
2,096(8) |
O21 - Sb9 - C331 |
90,2(3) |
|
Sb7–C261 |
2,097(13) |
O21 - Sb9 - C321 |
90,5(7) |
|
Sb7–C241 |
2,104(17) |
O22 - Sb9 - C341 |
84,2(4) |
|
Sb9–O22 |
2,171(9) |
Sb9‒O21‒Sb91 |
180,00 |
|
Sb9–O21 |
1,9466(17) |
Sb1‒O1‒Sb2 |
148,1(4) |
|
Sb9–C341 |
2,060(11) |
Sb3‒O6‒Sb4 |
147,3(4) |
|
Sb9–C331 |
2,090(9) |
Sb7‒O16‒Sb8 |
157,7(5) |
|
Sb9–C321 |
2,117(19) |
Sb5‒O11‒Sb6 |
152,0(4) |
Обсуждение результатов
Одними из наиболее изученных производных пятивалентной сурьмы являются биядерные соединения [Ar 3 SbOC(O)R] 2 O [1 - 34], основное различие геометрии молекул которых заключается в строении фрагмента Sb–O–Sb. В большинстве случаев фрагменты имеют угловую форму и лишь иногда линейную. Также известны кристаллы, в ячейках которых одновременно присутствуют молекулы (Ar 3 SbX) 2 O (Ar = Ph, p-Tol; X = CH 2 Cl, CH 2 Br) с угловым и линейным центральными фрагментами [39]. Факторы, влияющие на величину угла при мостиковом атоме кислорода, не выяснены, и нельзя спрогнозировать, линейную или угловую форму будет иметь фрагмент Sb–O–Sb той или другой молекулы, однако исследование структур данного типа может позволить определить какие-либо закономерности в производных указанного типа. В настоящей работе синтезированы и кристаллографически охарактеризованы пять неизвестных ранее биядерных арильных соединений сурьмы, представляющих интерес для получения иных сурьмаорганиче-ских производных. Известно, что кристаллы подавляющего большинства ковалентных сурьмаор-ганических соединений содержат один или два типа кристаллографически независимых молекул [40]. Однако в некоторых случаях число типов кристаллографически независимых молекул кристалле может быть больше, как, например, в кристалле трис (4- N,N -диметиламинофенил)сурьмы с четырьмя типами кристаллографически независимых молекул [41].
По данным РСА следует, что кристаллы комплексов 1 - 5 состоят из биядерных молекул с угловым фрагментом Sb-O-Sb (рис. 1 - 5), причем в кристаллах присутствуют: 1) один тип кристаллографически независимых молекул с углами SbOSb 144,5(5) ° для 1 и 152,12(14) ° для 2 , 2) два типа кристаллографически независимых молекул с углами SbOSb 139,88(14) ° и 179,998(2) ° для 3, 139,8(3) ° и 179,999(1) ° для 4 , 3) пять типов кристаллографически независимых молекул с разными значениями угла SbOSb [147,3(4) ° , 148,1(4) ° , 152,0(4) ° , 157,7(5) ° , 180,00 ° ] для 5 .
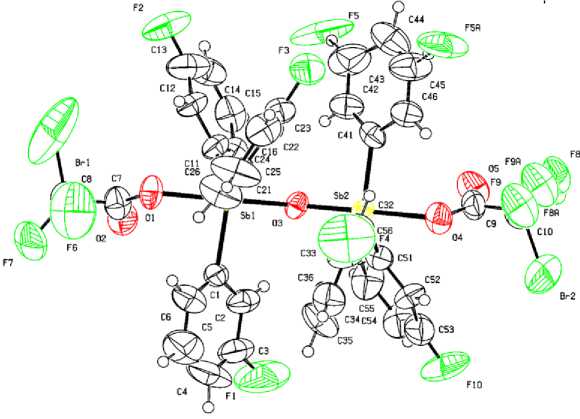
Рис. 1. Общий вид комплекса 1
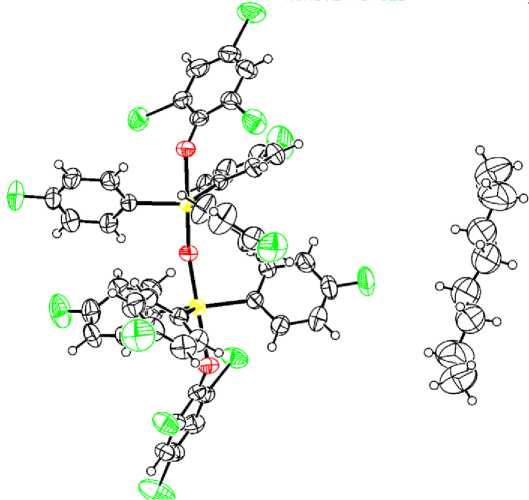
Рис. 2. Общий вид комплекса 2
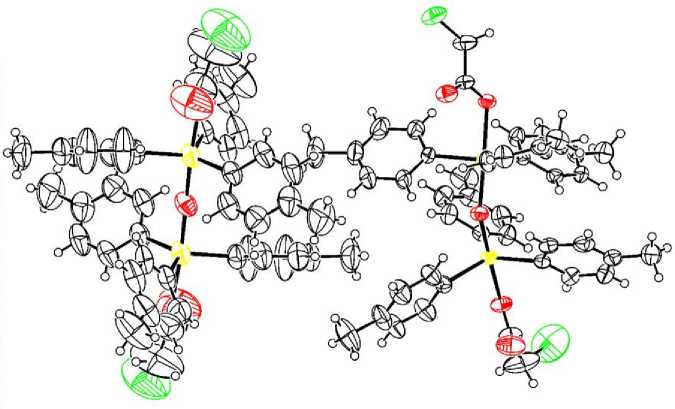
Рис. 3. Общий вид комплекса 3
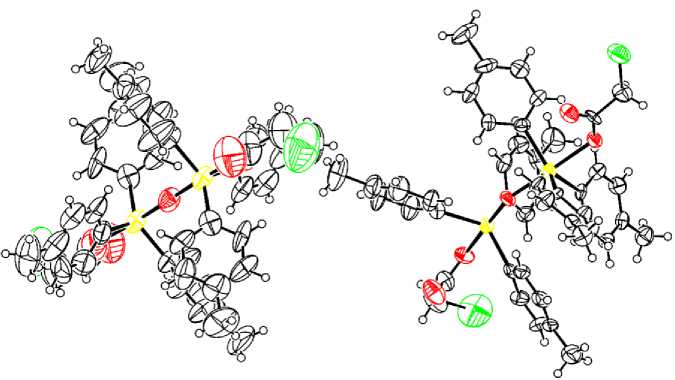
Рис. 4. Общий вид комплекса 4
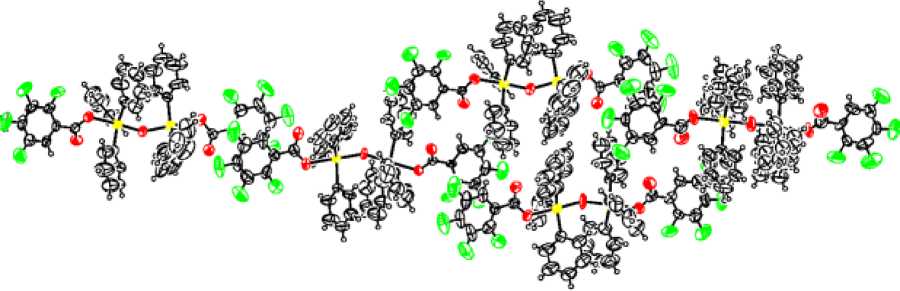
Рис. 5. Общий вид комплекса 5
Длины связей и значения валентных углов в структурах соединений 1 - 5 близки к наблюдаемым в аналогичных известных структурах [4].
Выводы
Методом рентгеноструктурного анализа определено строение пяти биядерных арильных соединений сурьмы, в кристаллах которых присутствуют: 1) один тип кристаллографически независимых молекул с углами SbOSb 144,5(5) ° для 1 и 152,12(14) ° для 2 , 2) два типа кристаллографически независимых молекул с углами SbOSb 139,88(14) ° и 179,998(2) ° для 3, 139,8(3) ° и 179,999(1) ° для 4 , 3) пять типов кристаллографически независимых молекул с разными значениями угла SbOSb [147,3(4) ° , 148,1(4) ° , 152,0(4) ° , 157,7(5) ° , 180,00 ° ] для 5 .


