Новые гиперболические модели многокомпонентных гетерогенных сред

Односкоростные модели многокомпонентной среды используются при моделировании волновых процессов во вспененных жидкостях и полимерах [1], в пузырьковых жидкостях [2], для локализации контактных поверхностей в многожидкостной гидродинамике [3]. Включение в уравнения смеси сил вязкого трения и теплопроводности расширяет сферу приложения модели и дает возможность проводить расчеты течений, например, углеводородных смесей, биологических жидкостей и т.д. В литературе, помимо использованной в настоящей работе модели односкоростной смеси из [4], имеются и другие гиперболические модели, описывающие течения бинарных смесей (см. [5-7]), которые, в отличие от [4], не распространяются на. случай с произвольным числом фракций в смеси.

Если при рассмотрении явления распространения тепла, в односкоростных гетерогенных средах воспользоваться законом Фурье, то тепловые волны будут перемещаться с бесконечными скоростями. Если же вместо закона. Фурье применить закон Максвелла. - Каттанео [8-9], учитывающий релаксацию теплового потока, то движение волн происходит с конечными скоростями, что в свою очередь связано с принадлежностью системы уравнений к гиперболическому типу [10].

Включение сил вязкого трения в уравнения модели односкоростной многокомпонентной среды из [4] также приводит к появлению волн с бесконечно большими скоростями распространения. В настоящей работе представлена, модель среды, свободная от этого парадокса, в которой по аналогии с подходом Максвелла. - Каттанео в теплопередаче также учтена, релаксация вязких напряжений.

Вязкие напряжения вводятся в уравнения модели односкоростной многокомпонентной среды из [4] на. уровне смеси в целом, которые по виду совпадают с газодинамическими. В газовой динамике широко используется упрощенная формула, для расчета, вязких напряжений [11], которая для одномерных течений имеет вид

∂u

σ = µ_∂x,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ где р - коэффициент вязкости. Но применение этого соотношения приводит к потере гиперболичности исходной системы уравнений. Чтобы остаться в рамках гиперболической системы, вместо выражения (1) предлагается использовать соотношение

( дт + и^т ) + ^а = 4т ⁽²⁾ ∂t ∂x ∂x

Подобный прием впервые использовался в теплопередаче для исключения парадокса, связанного с бесконечной скоростью распространения тепловых волн. С точки зрения физики это означает, что силы вязкости начинают действовать не мгновенно, а в прошествии времени релаксации т_а.

Отметим также, что уравнение (2) есть упрощенный вариант реологического выражения для жидкости Максвелла [12]. С этой точки зрения смесь в целом может рассматриваться как вязкоупругая среда. Для вязкоупругих жидкостей время релаксации может быть найдено из соотношения т_а = p/G, где G - модуль упругости смеси.

При рассмотрении многоскоростных сред в работе использовалась модель гетерогенной среды из [13], основанная на законах сохранения. Особенность этой модели состоит в том, что в ней вводится такое состояние среды как смесь в целом, характеризуемая осреднен-ными значениями скорости, плотности и т.д., уравнения для которых по виду совпадают с газодинамическими. К этим уравнениям добавляются соотношения, выражающие законы сохранения для отдельных компонентов смеси. Давление полагалось общим для всех фракций смеси.

В настоящей работе использована модификация модели из [13], учитывающая вязкие и теплопроводящие свойства смеси.

1.    Гиперболическая модель односкоростнойвязкой теплопроводной среды

Рассмотрим n-компонентную смесь с первыми m сжимаемыми фракциями [4], в уравнения которой включены эффекты вязкости и теплопроводности

∂

τW

∂t ∂ W ("д Т ⁺

∂ρ dt + div(р u) = 0,

^p(^{E +} 2 ^{| u} l '²)

( u •V )w) + x VT + W = 0 ,

+ div р

∂ u

^p[at ^{+ (u   )u}]

( ^{E +} 2 ^{| u}l

+ V ( p — a ) = F ,

² + p

-

σ

ρ

u + W = F • u ,

∂αiρ_i ⁰ ∂t

Т" ^дт+ + ( u ^ V ) ^a) — ^ div ( u ) + ^a = 0; n

+ div ( aip ⁰u) = ^Sik Jik, k =1

^{P i      +(u} • ^{V ) £}")

+

n

αip

δik Jik

ρ

-

ρi

n

= Д Sik Qik k=1

k =1

n

-

( Ei - 2 l u 12) Ё Sik Jk,

n

k =1

daj .   ,    .    1 A_

7 + div ( aj u ) = V Sik Jjk, j ∂t                  ρj ⁰ _{k =1}

(di ^{+ (u} ^ ^V ) ^p 0

г = 1 ,..., it i — 1;

= m + 1 ,... ,n.

Поведение сжимаемых фракций описывается калорическими уравнениями состояния Ei = Ei(p,р0), поэтому выражение для удельной внутренней энергии смеси, учитывая равенства 52n=i ai = 1, р = 52n=i Pi, может быть записано как е = е (р, p ,a 1 ,р 0,.. .,am-1 ,рm— 1, am+1,.. .,an).

Среднюю температуру определим в соответствии с формулой

n

T = ^ a-Ti, i=1

где T- - локальная температура г-й фракции, которая находится из термического уравнения состояния T- = T- ( p,р ?). Формулу (5) перепишем так

T = T ( р, p, a 1 ,р 0 , ... ,am— 1 ,р m- 1 , am +1 , ... ,a_Tl ) .

Можно показать, что система уравнений (3) при отсутствии массовых сил, фазовых и химических превращений для одномерных плоских течений приводится к виду

др   Ip    l“      l“ l“  1 Ip

∂t   u∂x   ρ∂x    ,  ∂t   u∂x   ρ∂x

-

|? + “i T + рс 2 du + H^W =0 ' ∂t ∂x ∂x     ∂x

1 да

= 0 , ρ∂x

где

∂W ∂t

∂ρ_i ⁰ ∂t

кр =

∂W

⁺ “

∂x

∂ρ ⁰

+ u i-∂x

χ ∂T τW ∂ρ,

+ k др + k дР + v1 (k .^ + k 0 др? ρ ∂x    p ∂x          i ∂x ρi ∂x i=1

∂σ ∂σ

It ⁺ “ix

-

µ ∂u  σ

Ta lx   Тст ’

n

+k j=m+1

∂αj

α j ∂x

+ W =0

^TW        (7)

0  ∂u     ∂αi    ∂αi∂u

+ PгGi"^EГ" =0 ,     + “ "я--+ a- (1 — G- фд^- = 0 , г = 1 ,...,?/г — 1;

i   ∂x      ∂t      ∂x∂x

-Е ^ + u^j + aj -u = 0 , j = m + 1 ,..., n,

∂t     ∂x∂x

χ ∂T       χ ∂T        χ ∂T kp = tw др1  ка 1 = tw la 1'  kp 1 = tw др?'

...,

kα n

χ ∂T τW ∂αn .

Соответствующие выражения для H, G- и адиабатической скорости звука

с имеют вид

н = ¹ Г ^1е +      ^1е - / ^1е - \ ¹ /

ρ ∂p   _{i =1} ∂p ∂ρ_i ⁰

αi ∂ε    ∂ε

- 1

с =

p-σ

ρ

-

∂ε ρ_∂ρ

-

ρ_i ⁰ ∂αi ∂ρ_i ⁰

_ m^{- 1} Г Р__Эе_ ( pE i ) ^- _{i =1} ρ i ⁰ ∂ρ i ⁰ ∂ρ i ⁰

,

1     -1 (К i  р0 IW    р0

¹ + “< (1 - p (< р ?)² эе о ) ^- 1)]

-

-

∂εi ^{ρ c 2} ∂p ^,

n

Е «j ^з j=m+1

р I" Эе + m y¹ dEi ( pEi, ) ¹ ( ^р др ⁺ i =1 др у dpi / у

^α i ∂ε

ρ _i ⁰ ∂α i

_- ∂ε ∂ρ _i ⁰

.

Систему уравнений (7) перепишем в векторной форме

⁸"U +A ^dU = S ' ∂t ∂x

где

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

U = ( р, u, p, ст, р °,	,α 1 ,	... , ρm - 1 , αm - 1 , αm +1 , ...	,an, W )T
S = (0 ,	0 , 0 ,	-ст / тст, ... , 0 , -W / TW )т ,

u		ρ	0	0	0	0	...     0	0	0      ...	0	0
	0	u	1 /Р	- 1 /р	0	0	...     0	0	0      ...	0	0
	0	ρc 2	u	0	0	0	...     0	0	0      ...	0	H
	0	- ^/тст	0	u	0	0	...     0	0	0      ...	0	0
	0	ρ 01 G 1	0	0	u	0	...     0	0	0      ...	0	0
	0	a 1(1 - G 1)	0	0	0	0	...     0	0	0      ...	0	0
A =	... 0	... ρ 0 m- 1 G m - 1	... 0	... 0	... 0	... u	...     ... ...          0	... 0	...     ... 0      ...	... 0	... 0
	0	am- 1(1 - Gm- 1)	0	0	0	0	...     u	0	0      ...	0	0
	0	αm +1	0	0	0	0	...     0	u	0      ...	0	0
	... 0	... αn	... 0	... 0	... u	... 0	...     ... ...     0	... 0	...     ... 0      ...	... u	... 0
	kρ	0	kp	0	kρ 01	kα 1	... kρ 0 m- 1	kα m - 1	α m +1     . . .	kα n	u

Здесь Т - оператор транспонирования. Характеристическое уравнение системы (7) имеет вид

[ е - ( и — С 1)] [ е - ( u - c 2)] ( С - u ) n + m ² [ С - ( u + c 2)] [ С - ( u + c 1)] = 0 ,          (9)

где е = dx/dt- Значения скоростей c 1 и c2 рассчитываются по формулам c1

2 {с ² + ш 2+ kpH + Z} ,

c 2

X^ K +^+ZHHZZ^,

где ш 2=- К-, ρτ σ ,

Z =

с 4+ H kp (2 c 2+2 ш ²+ k_pH ) + 4I k_p +—

m- 1                                n

^ (kp0PiGi + kaia(1 -Gi)) + ^ kaj “i i=1                              j=m+1

Корни характеристического уравнения (9) - действительные числа. Кроме того, матрицу A можно представить в виде

A = И ^- 1ЛИ ,

поэтому система (7) гиперболическая. Отметим, что система (7) к дивергентному виду не приводится.

Для бинарной смеси идеального газа с несжимаемой второй составляющей газодинамическая часть системы уравнений (7) имеет вид

™ с = ^ ^ (^

d^p + и⁸/ + p-u = 0 , ∂t ∂x ∂x

H =

γ- 1

α

∂u

∂u

1 д ( p — ст )

-t ⁺ u-x ⁺-

ρ

-p + u-p + pc 2 -u + H-W =0, ∂t ∂x ∂x ∂x да да (1 — a) -u =0, ∂x

д t ⁺ udx

-

α

∂x

= 0 ,

(П)

объемная доля газа в смеси. Выражение для закона Фурье

с тепловой релаксацией, учитывая соотношение T = T ( р,р,а ) , перепишем как

∂W   ∂W    ∂p   ∂ρ   ∂α W

∂t   ^u ∂x     ^p ∂x    ^ρ ∂x    ^α ∂x          ^,

τW

где

kp =

χ ∂T

τW ∂ρ,

kp =

χ ∂T

τW ∂p,

kα

χ ∂T

τW ∂α.

где

Систему (2), (11) и (12)

U =

представим в векторной форме (8), в которой

(

V

ρ

u

p

σ

α

W

\

/

, А =

u

ρ

u

ρc ²

1 /Р

-

1 /Р

(

\

u

H

-ρω ²

u

,

S =

-

σ

.

V

α

-

u

kρ

kp

kα

u

/

V

-

W / TW /

Матрица А имеет шесть действительиых собственных значений: u ± с 1 ,

u,

u,

u

± c 2

^{с 1}=Д

с ² + ш ² + kpH +

У с ⁴ + H [ kp [2(

с ² + ш 2) + kpH ] + 4 ^Рр

-

с 2 =

с ² + ш ² + kpH

-

У с ⁴ + H [ kp [2(

с ² + ш ²) + kpH ] + 4 ^ kp

-

Отметим, что с 1 определяет скорость распространения газодинамических возмущений,

а с 2

тепловых. Соответствующие матрицы Q

и Л в представлении (10)

имеют вид

Q =

-

k ρ

c 1

k ρ

c 1

-

k ρ

c 2

k ρ

c 2

V

Л =

V

2 c

ρ _H ¹

c ² ₁ ρ_H

2 ^c

ρ _H ²

2 c

ρ _H ²

-

-

-

-

kp

kp

kp

kp

-

c 1

H

c 1

H

-

c 2

H

c 2

H

— f cl — kA c1 H - kp f cl   kA c1 H - kp

1 ( H — kp )

( H

-

-

-

kp

-

k _α

c 1

k α

c 1

-

k α

c 2

k _α

c 2

c 2

u

0 0 - c 1	0 0		0		ρ - α- 1 ρω 2 α- 1 0 \
			1 0	0
	0	0
0	и + с 1	0	0	0	0
0	0     и	- c 2	0	0	0
0	0	0	и + с 2	0	0
0	0	0	0	u	0
0	0	0	0	0	u

.

/

,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Подробнее рассмотрим пузырьковую жидкость. Без потери точности можно считать, что температура несжимаемой фракции постоянна, т.е. T 2 = const, поскольку ее доля в смеси значительна. Это предположение снимается при учете сжимаемости жидкости. Выражение для средней температуры (5) дает

T =

_α 2 _p

^{[ р — р 0(1 — а )]} R

⁺⁽¹ — ^а ) T о ,

где T о - начальная температура среды, R - газовая постоянная. С использованием (16) коэффициенты кр, кр и к_а, которые входят в соотношения (14), принимают вид:

кр =

—

α ² χp

^TW ^[ Р ^— Р 2⁽¹

_α 2 _χ

— а )]² R^-

kα

kp    t w [ р — р 0(1 — а )] R,

. X / ^аР ⁽2 р ^{+ а}р ⁰⁾    _ T \

^TW U Р — Р 2(1 — а )]² R °/ ■

В частности, для водно-воздушной смеси при нормальных условиях и объемной доле газовой составляющей а = 0,1 ( р *2=1000 кг/м³), значения скоростей с i, с 2 и с равны 39,38, 2,06 и 39,44 м/с соответственно. В расчетах коэффициент теплопроводности смеси определялся из выражения

X =- (Р1X1 + Р2X2) -ρ где X 1 =2- 58 х 10~2 I<г-м (с3 К) - для воздуха. X2 = 60, 2 х 10_2 i<г-м (с3 К) - для воды, а коэффициент tw =10 с [14]. Вязкость смеси полагалась равной вязкости жидкости ц = 10~3 кг/(м с), т,= 0,1 с. Значения определяющих параметров гетерогенной смеси, в отличие от «чистых» газов, сутпествешю зависят от коэ<])<])ипиепта тепловой релаксации tw 11 в меньшей степени от ц и т,.

2.    Модель многоскоростной вязкой теплопроводной среды

Для бинарной смеси с объемной долей идеального газа а и несжимаемой второй составляющей уравнения многоскоростной модели из [13], в которой дополнительно учтены вязкостные и теплопроводящие свойства смеси, принимают вид где

∂p dt ⁺

∂ρ ∂ρ ∂u     ∂u di + «аХ + РаХ = 0’  ай

∂α аХ + *

∂u u∂x

1 д ( р — ст )

ρ

∂x

= 0 -

*ap + рс ² а* + Ha =0 - т, (% + .#) ∂ x ∂x ∂ x           ∂t ∂x

∂W    ∂p   ∂ρ   ∂α  W

∂W

s

∂t ∂α д x

σ

∂u

⁺ ° = ^цаХ-

W

∂x     ^p ∂x    ^ρ ∂x    ^α ∂x τW ^,

c

∂u s — (1 — а ) аХ	=0 - а* + * s ∂t	∂u s ∂x	1 Эр (ааа ρ s ∂ x ∂ x
/ Y ( Р — 0 )	н-Y — 1	G =	p
αρ ,	H          - α		(1 — а ) р s -
кр = XdT-	кр = x?T-	ка =	χ ∂T .

= S,

τW

τW

τW

Характеристическое уравнение системы (18) определяется из соотношения

	t-u	-р	0	0	0	0	0
	0	t-u	- 1 /р	1 /р	0	0	0
	0	-рс 2	t-u	0	-H	0	0
	0	µ/τσ	0	t-u	0	0	0	= 0 ,
	- kp	0	- kp	0	t - u	- ka	0
	0	0	0	0	0	t - us	1 - а
	0	0	- 1 / рs	0	0	G	t - us
или, раскрывая определитель,			получим

А ( С ) = [( ^-u s)2 - (1 - а ) G ] ( ^-u )5+

⁺ { (--- р^ --[⁽ ^-u s )2 - ⁽¹ - ^а ) G ] ( с ² + kpH + р| -^} ⁽ ^-u )3⁺

+ { H ^[( - s)² - (1 - а ) G ^] ( £* - kp ) - ^{Р (1} -,“>k ^a H } ( t-u ) = 0 .

Выписать аналитические выражения для всех корней уравнения (19) не удается. Однако, если в выражении (19) положить к_а = 0, то оно преобразуется к виду

А 1(t) = (t-u) [(t-us)2 - (1 - а)G] Х х [(t-u)4 - (с2 + kpH+^ (t-u)2 - (kp - ^ h] = 0,            (-0)

корни которого u, и ± с 1, и ± с2, us ± с3, где с2 =

c 1

-Д

с ² + ш ² + kpH +

с ⁴ + H ( kp [2( с ² + ш 2) + kpH ] + 4 kp

) ,

vTp+ " 2+

kpH -V

с ⁴ + H ( kp [2( c ² + ш 2) + kpH ] + 4 kp

) ,

Отметим, что для газожидкостных систем условие к_а = 0 практически не меняет вид характеристического полинома, что видно из рис. 1, где приведены зависимости А ( t ) и А i( t ) для водно-воздушной смеси с параметрами: а = 0 , 9, T о = 293 К, р ⁰ = 1 , 19 кг/м³, у =1,4, р _s =1000 кг м³. х = 2 , 58 х 10 ^{_ 2} i<г - м (с³ К). х s = 60 , 2 х 10 ^{_ 2} i<г - м (с³ К). t w = 10 ^{_ 2} с. р = 0,01 кг/(м с), т_а =0,1 с. С точностью до графического представления полиномы (19) и (20) совпадают. Для других многокомпонентных систем условие к_а = 0 может оказаться неприемлемым, в этом случае корни характеристического уравнения необходимо определять численно из (19).

3.    Автомодельные решения

Решение системы (7) будем искать в виде р = р(t), u = u(t) Р = Р(t), a = a(t), W = W(t), р0 = р^t) ai = ai (t) Pj = Pj (t) г4е t = x - Dt- При учете соотношений d    d dt       d    d    d dt   d

∂t   dξ ∂t       dξ ,   ∂x   dξ ∂x   dξ ,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

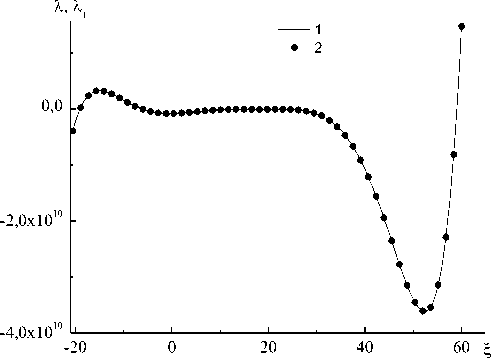
Рис. 1. Зависимости А(£ ) и A ₁( £ ) (кривые 1 и 2) для водно-воздушной смеси

система (7) приводится к

системе обыкновенных дифференциальных уравнений:

dρ du

⁽ u - D ' dp ⁺ pd« = ⁰

dW dρ

^{( u - D} )   ⁺ kp i

(и - D)   + 1 ip- dξ ρ dξ

Д m- 1 /

+ kp ip + e ( k. .

-

1 °^- = 0 ,  ( и - D ) dp + pc 2 du + HdK =0 ,

ρ dξ               dξ dξ dξ

riai      rip ⁰ A ^e      da₃

^^{+ k p} 0    ⁺ j = m +1 ^kj ®d

+ К = 0 , τW

( и - D ) i-

-

n “и a        , d dp 0     пи dti

— + - =0,  (и - D)p + p0GiЛ7 = 0, dξ        dξ

τσ dξ

τσ

(и - D) dai + а (1 - О,) du =0, dξ             dξ dα du

^{( и} - D ) nt ⁺ а т₆ = 0 , ' =

i. = 1 ,..., n i - 1;

m + 1 ,..., n.

В частности, для бинарной смеси идеального газа соответствующая система уравнений запишется как

с несжимаемой второй составляющей

( u - D ) £ + Pc ² iu + H- =0 , dξ dξ dξ

-

1 ia

= 0 , ρ dξ

( и - D ) “К + kp is + kp ip + k. ^ + - =0 , dξ dξ     dξ dξ τW

( и - D ) i^- - A“ ^u + ^- =0 ,  ( и - D ) OU - (1 - a ) “^и =0 .

dξ   τσ dξ τσ                dξ          dξ

-

Систему (22) перепишем в удобном для интегрирования виде

где

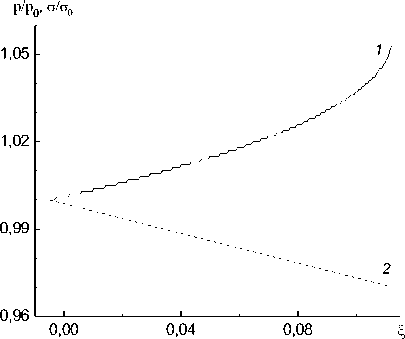
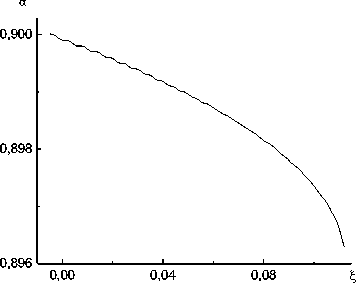
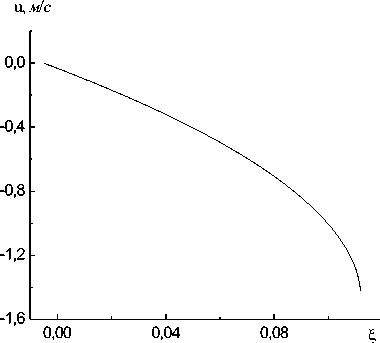
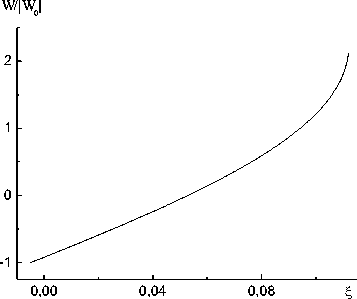
Рис. 2. Зависимости p ( £ ) /p 0 (кривая 1), a ( £ ) /a 0 (2), u ( £ ), a ( £ ), W ( £ ) /|W 0 | для водновоздушной смеси (односкоростная модель)

dW dξ

dp dξ

du = * , d? = а ^ф , dξ        dξ

= ф |^ H ^kpA + PaB -

£ = E » + F, ^ = B » , dξ              dξ

EW τWF

= ф ^{р 2    + kpF}) ^{- ( u} - D ⁾   W

) ^-p ⁽ u ^- D ) ( c ²

^^^^^^^^.

HW

τWF ,

^[ р ⁽ u — D ) — E ] + F ⁽ kpA + kaB ) } ] ,

A =

^^^^^^^^.

ρ u - D’

B = - u

^^^^^^^^.

^^^^^^^^.

Ф = ( u - D ) Рр [( u - D )

α

D^, 2

-

E =

^    . F =

T_a ( u - D )           T_CT ( u - D )

c 2] - kPH - uE} + H ( kpA + kaB ) ,

^ф = F [< u ^- D ^{)2 -H} ( ^{P p +} T^)] •

В качестве примера рассмотрена задача о движении волны по неподвижной однородной газожидкостной смеси с параметрами: а о = 0,9, T о = 293 К, р 0о = 1 , 19 кг/м³, y = 1,4, р s = 1000 кгм3. х = 2 , 58 х 10 ^{_ 2} i<г - м (с³ К). х s = 60 , 2 х 10 ^{_ 2} кг м (с³ К). t w = 102 с. д = 0,01 кг/(м с), т_ст = 0,1 с. Скорость перемещения волны полагалась равной D= 39,112 м/с.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Отметим, что из-за особенностей в системе (23) найти распределение параметров во всем фронте волны не удается. С использованием численного метода Рунге - Кутта решалась задача Коши на отрезке от i- = 0,005 до ближайшей особой точки. На рис. 2 приведены результаты вычислений для варианта: p ( i- ) = 0,1 МПа, и ( i- ) = 0, W—i— ) = — 103 Дж/(м² с), а ( i— ) = 104 Па.

При рассмотрении многоскоростной модели, учитывая соотношения (18), система (17) приводится к системе обыкновенных дифференциальных уравнений:

dρ du

^{- u —} D ' di ⁺ p^ =0 ,

^{( u —}

- us—D ) di —

(u — D) du + 1 dp =0,  (u - D) dp + pc2 du + HddW = 0, dξ ρ dξ               dξ dξ dξ dW

dρ

dp

dα

D) dW + kp dds+ kp dp + ka   + W =0, dξ dξ dξ dξ   τW

dξ ^ρ dξ ^p dξ

(1 — a)     = 0, (us — dξ

dξ du

у dp ' di ⁺ p . di

dξ

-

G^ = S. dξ

где

Перепишем (24) в удобном для интегрирования виде

du dξ

= Ф, dP = A Ф ,d| = B Ф, dp = M Ф + L, dξ       dξ          dξ dσ          dW

-=KФ+L, —=P Ф+R, dus dξ ,

Ф =

u-D,

B =

M = K — p ( u — D ) ,

4 —a. к =    ^   .

u s — D       To ( u — D )

M ( u — D ) + pc ²

P =        H ,

L =

R =

σ

-

-

To ( u — D ) L ( u — D )

H,

X = ( u — D ) P + kaA + kpM,  Y = —kpL — ( u — D ) R — W / t w .

p s Y ( u s — D — BG ) + kaB ( L — p s S )             MY + X ( L - p s S )

p _s X ( u _s — D - BG ) — k_aBM   ,       p _s X ( u _s — D - BG ) — k_aBM"

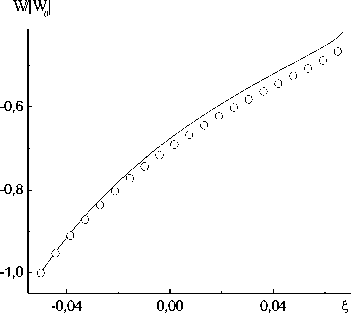
Как и в предыдущей задаче решалась задача Коши на отрезке от i- = - 0,005. На рис. 3 представлены результаты интегрирования системы (25) для вариантов с коэффициентом k_a, равным нулю и рассчитанным по формуле (17). Исходные данные для задачи следующие: D = — 39 , 178 м с. p ( i- ) = 0.1 XШа. и ( i- ) = 0. U s( i- ) = 0. Ж( i- ) = — 103 дж (м² с). а ( i- ) = 104 Па, S = 0. Параметры водно-воздушной смеси те же, что и в первом примере.

Полученные решения автомодельных задач могут быть использованы при тестировании численных методов, разрабатываемых для интегрирования общих уравнений моделей (3) и (18).

Заключение

Представлены модифицированные модели одно- и многоскоростной многокомпонентной среды, учитывающие вязкостные и теплопроводящие свойства смеси. Показано, что при использовании релаксационных законов для диссипативных процессов системы уравнений относятся к гиперболическому типу. Для рассматриваемых моделей среды исследованы автомодельные решения типа бегущих волн, которые в дальнейшем могут быть использованы при конструировании решателей задачи Римана, используемых в численных схемах годуновского типа.

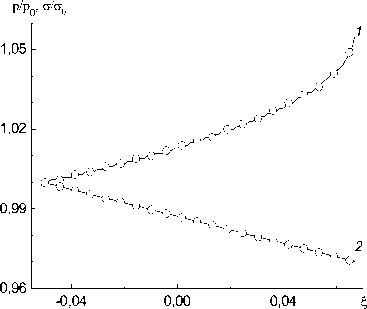
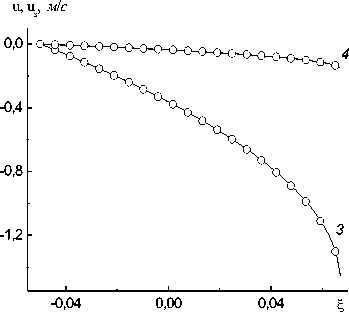
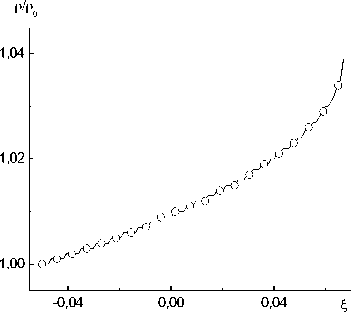
Рис. 3 Зависимости р ( £ ) /р о (кривая Л- а ( £ ) /ао ЛY и ( £ ) Л). и ( £ ) Ц ). р ( £ ) /р о. W ( £ ) /|W 0 I Д^ля водио-воздушной смеси (миогоскоростиая модель). к _а из (17) - сплошные кривые: к _а = 0 - кружочки

Обозначения с - скорость звука в смеси; c*i, Yi, P*i ~ константы уравнения состояния; D - скорость перемещения волны; т - число сжимаемых фракций в смеси; п - общее количество фракций; р - давление; u - вектор скорости; F - плотность массовой силы; Jj - интенсивность превращения массы из г-й фракции в у-ю на единицу объема смеси; Qij - тепловыделение в единицу времени на единицу объема смеси вследствие превращения г-й фракции в у-то; T 11 W - осредпеппые температура и век тор плотности теплового потока: ai - объемная доля г-й фракции в смеси; 5j - символ Кронекера; £ - автомодельная переменная; р - плотность смеси; р0- истинная плотность г-й фракции; рs- плотность несжимаемой фракции; pi = aip0 - приведенная плотность г-й фракции; Ei - удельная внутренняя энергия г-го компонента; ст - вязкое напряжение; р - коэффициент вязкости; х ~ коэффициент теплопроводности смеси; tw ит^- времена тепловой релаксации смеси и релаксации вязких напряжений. Индексы: О-в невозмущенной среде; г - для сжимаемых фракций; j - для несжимаемых.