Новые возможности модели Четаева

Экспериментальные исследования магнитотеллурического (МТ) поля обнаруживают целый ряд эффектов, не согласующихся с моделью однородной вертикально падающей плоской волны [Тихонов, 1950]. Прежде всего, это всюду наблюдаемая горизонтальная неоднородность МТ-поля, которая по традиции объяснялась наличием горизонтальных неоднородностей среды. В 1969 г. профессор Дмитрий Николаевич Четаев [Четаев, 1969] предложил модель локального описания МТ-поля в окрестности точки наблюдения неоднородной плоской волной, распространяющейся горизонтально вдоль поверхности Земли. «Возможность локального описания поля именно плоской волной, — писали авторы [Че-таев и др., 1980], — является следствием его непрерывности. В достаточно малой окрестности, где пространственные изменения компонент поля линейны, естественно аппроксимировать поле плоской волной, определяемой этими линейными приращениями комплексных амплитуд». Дальнейшие размышления привели Четаева к созданию дирекцион-ного анализа (модели Четаева). Предпосылки и история его построения подробно описаны в работах [Четаев и др., 1980; Четаев, 1985]. Ключевая идея дирекционного анализа — возможность исследования благодаря определению комплексных горизон- тальных компонент волнового вектора kх, kу из уравнений Максвелла (в слое с проводимостью σ) фазовых скоростей горизонтального распространения МТ-поля, пространственных затуханий, направления распространения волны (дирекционного угла), элементов эллипсов поляризации и кажущегося сопротивления разреза. Дирекционный анализ дает инструмент для разделения полного МТ-поля на пятикомпонентные h- (Нz≠0) и e- (Ez≠0) моды. Благодаря тщательно выполненным экспериментам [Четаев и др., 1980] Четаеву с сотрудниками удалось объяснить горизонтальную неоднородность МТ-поля не влиянием горизонтальных неоднородностей среды, а лишь свойствами неоднородной плоской волны, реализуемой суперпозицией горизонтально распространяющихся неоднородных h- и e-мод. Хотя ответ на вопрос о природе Еz-компоненты до сих пор неоднозначен [Анисимов и др., 1993], специалисты уже не ставят под сомнение возможность использования дирекционного анализа на высокоомных разрезах.

Существуют по крайней мере два эффекта в МТ-поле, не получившие теоретического обоснования. Речь идет о необычном направлении (из земли в воздух) вертикальной компоненты вектора Пойн-тинга Sz и аномалиях коэффициента отражения Q . Подобные факты были обнаружены в целом ряде экспериментальных работ (см. ниже). В статье рассматриваются аномальные потоки энергии S_z <0

Таблица 1

Энергетические параметры МТ-поля геомагнитных пульсаций.

Волчинка, июль 1988 г.

Число	Интервал времени	Т , с	Re S z	Im S z	| Q h|	| Q e|
15-	11.14.37–11.15.05	24.7	–44.70	6.70	0.95	1.4
15	15.36.14–15.37.02	23.7	–102.00	49.40	–	–
15	16.29.10–16.30.04	81.0	1.14	–1.86	0.73	4.5
16	0.357.40–04.02.03	95.0	41.90	–38.80	0.59	1.4

и коэффициенты отражения | Q |>1 с точки зрения дирекционного анализа.

Действительно [Стрэттон, 1948], при падении плоской электромагнитной волны на границу горизонтально-стратифицированной среды мгновенное значение вертикального потока энергии

Sz ( t )=[Re E ( t ), Re H ( t )] z , вряд ли имеющее физический смысл, может быть как положительным, так и отрицательным. Однако усредненное по времени значение

S_z = 1/2Re[ E , H *] _z ,                           (1)

где * — знак комплексного сопряжения, определяющее направление распространения энергии сверху вниз, должно оставаться положительным. Условия

S_z >  0,| 6 |=| р / A n ад | < 1,                            (2)

где Q — коэффициент отражения, А пад и А отр — амплитуды падающей и отраженной волн, в одномерной модели отражения не вызывают сомнения.

Изучению ситуации, когда не выполняются оба неравенства (2), посвящена работа [Савин, Израильский, 1991]. На основании результатов математического моделирования с использованием модели Че-таева, авторы обнаружили трехслойную модель, в которой модуль коэффициента отражения электрической моды | Q ^e|>1. Однако вопрос о магнитной моде оставался открытым. Исследования, результаты которых излагаются ниже, показали, что существует класс так называемых резонансных моделей, в которых коэффициент отражения не только электрической, но и магнитной моды превышает единицу, т. е. выполняется условие | Q ^h|>1. В настоящей работе дается изложение результатов численных расчетов отражения магнитной и электрической мод в трехслойных (резонансных) моделях. Обсуждается вопрос о правомерности интерпретации данных ди-рекционных магнитотеллурических зондирований (МТЗ) способом аналитического продолжения коэффициентов отражения вниз [Четаев и др., 1984].

ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ

На возможность получения аномальных (из земли в воздух) значений Sz < 0 впервые обратил внимание Ю.Б. Шауб с сотрудниками [Шауб и др.,1976]. Авторы сделали попытку объяснения обнаруженного ими парадокса перемещением локальных магнитных и электрических диполей или какой-то другой их нестабильностью. Исследование аномальных потоков энергии для целого ряда индивидуальных геомагнитных пульсаций типа Рс3, Рс4 [Гульельми, 1973] по наблюдениям в п. Татьяновка Приморского края проведено в [Шауб, 1982]. Подобная ситуация наблюдалась во время полевых работ в п. Волчинка на Северном Сахалине в 1991 г. Используя формализм дирекционного анализа [Четаев, 1985], авторы работы [Савин и др., 1991] обнаружили не только отрицательные вертикальные потоки энергии для пульсаций Рс3, но и аномальные, превышающие единицу, модули коэффициентов отражения для парциальных волн электрического |Qe| и магнитного |Qh| типа (табл. 1). Если обратиться к эксперименту по синхронной регистрации МТ-поля в трех пунктах на Украинском кристаллическом щите, выполненному в 1974 г. под руководством Четаева, обнаруживаются все те же аномалии. Подтверждением сказанного являются данные табл. 2, в которой приведена выборка аномальных значений модулей коэффициентов отражения |Qe| и |Qh| для 14 индивидуальных пульсаций Рс3, отвечающих нумерации табл. 1 (всего 50 пульсаций) из работы [Четаев и др., 1980]. Расчеты проведены нами для значений удельных сопротивлений верхнего слоя разреза 800, 1000 и 1200 Ом·м.

Возникает вопрос, являются ли обнаруженные факты закономерным явлением природы или систематической ошибкой эксперимента? В пользу первого предположения говорит тот факт, что энергетические аномалии МТ-поля были выявлены независимыми исследователями в различных геоэлектриче-ских условиях. Однако нельзя отбросить и второе предположение.

Нарушение закона сохранения энергии (2) несовместимо со свойствами однородной вертикально падающей плоской волны, поэтому при интерпретации МТ-поля по модели Тихонова–Каньяра все «неудобные» геомагнитные пульсации (например, приведенные в табл. 1, 2) должны быть отброшены. Если исключить ошибку эксперимента, мы оказываемся в ситуации, требующей теоретического объяснения.

Допустимо ли автоматически переносить энергетические закономерности вертикально падающих однородных плоских волн на горизонтально распространяющиеся неоднородные плоские волны? Этот вопрос принципиален для практических приложений. Достаточно вспомнить, что способ интерпретации МТ-поля аналитическим продолжением коэффициентов отражения вниз [Четаев и др., 1984] основан

Таблица 2

Модули коэффициентов отражения Рс3 по наблюдениям на Украинском кристаллическом щите.

Номер пульсации	R 01 =800 ом∙м		R 02 =1000 ом∙м		R 03 =1200 Ом∙м
	Q e	Q h	Q e	Q h	Q e	Q h
1	0.481	1.020	0.480	1.020	0.470	1.020
5	0.661	2.090	0.661	2.070	0.661	2.060
13	0.557	1.760	0.557	1.670	0.557	1.750
17	0.538	3.390	0.538	3.470	0.539	3.550
18	0.541	3.260	0.540	3.270	0.539	3.270
21	0.418	1.280	0.416	1.280	0.413	1.290
22	0.394	1.050	0.391	1.050	0.413	1.050
40	0.395	1.290	0.392	1.290	0.399	1.290
41	0.396	1.230	0.366	1.230	0.361	1.240
43	0.370	1.070	0.367	1.070	0.364	1.070
45	0.395	1.360	0.392	1.360	0.389	1.370
46	1.040	1.910	1.040	1.910	1.040	1.810
47	0.286	1.290	0.287	1.290	0.288	1.308
50	0.293	1.070	0.291	1.070	0.289	1.070

именно на выполнении условий S z = 0 и | Q e ^h( h )|=1 как предельных и определяющих глубины залегания геоэлектрических слоев при z = h . Эти условия используются для отбраковки индивидуальных геомагнитных пульсаций, не удовлетворяющих указанным условиям. С учетом результатов исследования магнитной моды [Cавин, Израильский, 1991] признание правомерности отрицательных потоков энергии для электрической моды и «аномальных» коэффициентов отражения | Q ^e| ограничивает возможности данного способа интерпретации. Поэтому не лишена интереса попытка найти объяснение указанным энергетическим аномалиям для магнитной моды при помощи модели Четаева.

ПОТОКИ ЭНЕРГИИВ МОДЕЛИ ЧЕТАЕВА

Выражения для действительных Re Z ^{e, h} и мнимых Im Z ^{e, h} частей импедансов электрического и магнитного типов запишем в виде [Четаев, 1985]:

Re Z ^e={ R +[ R ²+(ωµσ– J )²]^1/2}^1/2,              (3)

Im Z ^e= –(ωµσ– J )/{R+[R²+(ωµσ– J )²]^1/2}^1/2, (4) Re Z ^h=

=(ωµσ– J )/[ R ²+(ωµσ– J )²]^1/2{ R +[ R ²+(ωµσ– J )²]^1/2}^1/2, (5) Im Z ^h= –{ R +[ R ²+(ωµσ– J )²]^1/2}^1/2/[ R ²+(ωµσ– J )²]^1/2. (6) Здесь R =Re( k ² х + k ² y ), J =Im( k ² x + k ² y ), а kх =α х + i β x и kу =α y + i β y — горизонтальные компоненты комплексного волнового вектора k .

Из формул (3)–(6) видно, что в окрестности точки J кр =ωµσ парциальные импедансы претерпевают резкие изменения, а функции Im Z ^e и Re Z ^h меняют знак, причем при J > J кр

Im Z ^e>0, Re Z ^h<0.                          (7)

В диффузионном приближении теорема Пойн-тинга [Стрэттон, 1948] приобретает вид divS=–1/2σ|E|2+1/2iωµ|H|2,                 (8)

где вектор Пойнтинга S= 1/2[ E, H ^*].

Если проводящую область объема V ограничить замкнутой поверхностью Σ, джоулевы потери

• - 1/2 J V с |E| dV

должны быть скомпенсированы потоком энергии

• - Re <^, S _n d E ,

направленным внутрь объема. Поэтому, применяя теорему Гаусса к соотношению (8),

• [ div S dV = -( £ S n d E =

V 2 '                      2                    (9)

• = - 1/2 j V с |E| dV + 1/2 i иц [ |H| dV ,

приходим к неравенствам

Re f _z S n d E> 0,Im <^ _z S n d E< 0.             (10)

Из (10) следует, что среднее значение нормальной компоненты вектора S , <  S _n >  по замкнутой поверхности, не содержащей источников поля, должно удовлетворять неравенствам

Re f _z< S n >>  0,Im <  S n ><  0. (11)

Если взять в качестве объема V полупространство, а ось Z направить вниз, получим

Re <  S z >>  0,Im <  S z ><  0. (12)

Очевидно, что первое из этих неравенств отвечает представлениям о распределении энергии сверху вниз по направлению падающей на плоскость z =0 волны.

Как указывалось выше, дирекционный анализ основан на разделении полного МТ-поля на парциальные волны (моды) магнитного и электрического типа. Поэтому естественно рассматривать потоки энергии Snh и Sze для каждой из h- и е-мод в отдель- ности. С учетом выражений для парциальных импе-дансов Ze, h (cм. (21), [Четаев, 1985]) получим

E_x e, h = Z e, h H_y e, h , E_y e, h =– Z e, h H_x e, h .

Учитывая формулу (1), для парциальных волн е- и h-типов получим соотношение

S e" = 1/2 Z ^e,^h (| H x^ + H r' ) .              (13)

Следовательно, знаки действительной и мнимой частей вертикальной компоненты комплексного вектора Пойнтинга S _z ^{e, h} для обоих типов парциальных волн должны совпадать со знаками соответствующих частей парциальных импедансов Z ^{e, h}.

С учетом (12) приходим к выводу, что при любых значениях J должны выполняться неравенства

Re Z ^{e, h}≥0, Im Z ^{e, h}≤0.                        (14)

Эти неравенства отвечают функциям (3)–(6) во всей области определения параметра J за исключением функций Im Z ^e и Re Z ^h, которые при J > J кр должны удовлетворять условиям (7). Следовательно, при J > J кр

Re S n^h<  0, Im S z ^e'^h > 0,                          (15)

• т. е. нарушаются оба неравенства (12).

Таким образом, при распространении в слоистой проводящей среде неоднородной плоской волны мы сталкиваемся с парадоксальной ситуацией. Суть ее в том, что при значениях J > J кр энергия парциальной волны магнитного типа вопреки интуитивным представлениям течет снизу вверх, Re S ^ <  0. Кроме того, Im S z >  0, т. е. нарушается второе из неравенств (11).

Если вспомнить об экспериментально обнаруженных аномальных потоках энергии Рс3 геомагнитных пульсаций, то благодаря проведенному анализу, по крайней мере, некоторая часть данных получает теоретическое обоснование.

Попытаемся далее ответить на вопрос, насколько корректно проведен вывод условий (12).

Действительно, при этом использовалась теорема Гаусса (9), примененная к неограниченному объему (полупространству). В случае неоднородной плоской волны при х , у →–∞ подынтегральная функция неограниченно возрастает, так как

E , H — exp |^ i ( k x x + k y y ) ] —

~ exp[-(pxx + Pyy)]^«, Px,y > 0, а отвечающие им интегралы расходятся. Следовательно, применение теоремы Гаусса в рассматриваемой модели некорректно и «естественное» направление потока энергии Sz > 0 сверху вниз будто бы не следует из теоремы Пойнтинга.

Поэтому разумно (и, по-видимому, единственно верно) ориентироваться лишь на выводы, вытекающие из внутренних закономерностей модели Четаева, а именно, на свойства парциальных импедансов слоистых сред, приводящие к условиям (15).

Однако сами по себе аномальные потоки энергии кажутся противоречащими здравому смыслу. Дей- ствительно, МТ-поле падает сверху вниз, поскольку принято считать, что его источники находятся наверху, т. е. в магнитосфере и ионосфере Земли, а направление потока энергии этого поля прямо противоположно. Сделаем попытку внести хотя бы некоторую ясность в обсуждаемую проблему.

Известно, что вопросы, связанные с потоком энергии электромагнитного поля, едва ли не самые сложные в классической электродинамике. Если теорема Пойнтинга, выражающая закон сохранения энергии, в качестве полного интеграла [Стрэттон, 1948] выполняется безупречно, то вектор Пойтинга S определяется с точностью до произвольного вектора а , т. е. неоднозначно. «Вектор S — всего лишь вероятное выражение для потока энергии, — пишут авторы работы [Фейнман и др., 1977], — … Надо сознаться, что мы так и не знаем, как же на самом деле распределена энергия в электромагнитном поле… Ясно, что повседневная интуиция нас обманывает». Мы полагаем, что любое теоретическое исследование потоков энергии электромагнитного поля, будет нести в себе «первородный грех» — неопределенность потока энергии, поэтому, возможно, приведет к дискуссии, не имеющей перспективы быть когда-нибудь завершенной.

РАСЧЕТЫ КОЭФФИЦИЕНТОВ ОТРАЖЕНИЯ

Исследуем поведение коэффициентов отражения в модели Четаева.

Уравнения, определяющие зависимость парциальных потенциалов U ^{e, h} от глубины z [Савин, Израильский, 1986], удобно привести к единой форме

( zUʹ /η)ʹ–η Z 0 U =0,                             (16)

где n = ^k x + к У, — i ®Ц^ , а Z 0 — парциальный удельный импеданс. Входные парциальные импедансы Z для волн е- и h-типов могут быть единообразно выражены через парциальный потенциал U

Z =– Z 0 U ʹ/( U η).                               (17)

Внутри каждого слоя проводимость σ= const , поэтому решение уравнения (16) имеет вид

U ( z )= Ae ^{–η z} + Be ^{η z} ,                             (18)

где А , В — амплитуды падающей и отраженной волн.

Введем [Четаев и др., 1984] коэффициент отражения Q ( z ) на уровне z , имеющий смысл комплексного отношения амплитуды волны, идущей вверх, к амплитуде волны, идущей вниз,

Q ( z )= B / A exp(2η z ).                          (19)

Используя (17), получим следующую связь между коэффициентом отражения Q ( z ) и парциальным импедансами Z и Z 0 :

Z/Z0=[1–Q(z)]/[1+Q(z)], тогда

Q ( z )=(1– Z / Z 0 )/(1+ Z / Z 0 ).                     (20)

Поскольку входной (полный) парциальный импеданс Z зависит от глубины z непрерывно, а удельный импеданс Z 0 претерпевает разрыв на границе слоев, то Q ( z ) является кусочно-непрерывной функцией.

Формулы (19), (20), наряду с рекуррентными соотношениями [Дмитриев, 1970] для парциальных импедансов слоистой среды, позволяют вычислить коэффициент отражения в любой точке среды.

В случае однородной плоской волны (β х =0, β у =0) коэффициент отражения удовлетворяет неравенству

| Q ( z )|<1. (21)

Выясним, отвечает ли этому неравенству модуль коэффициента отражения для неоднородной плоской волны.

В случае двухслойной среды нетрудно провести аналитическое исследование коэффициента отражения

I Q i| = |( Z (o)i

i ii

Z (0)2 )' ( Z (0)1 + Z (0)2

где Z ( ₀ ) ₁ и Z ( ₀ ) ₂ — удельные парциальные импедансы в 1-й и 2-й средах, i=e, h. Опуская громоздкие выкладки, остановимся на результате. При R >0 модуль коэффициента отражения для обеих мод всегда <  1. Однако при R <0 оба коэффициента отражения по модулю могут быть больше единицы.

МАТЕМАТИЧЕСКИЙ ЭКСПЕРИМЕНТ

Обратимся далее к рассмотрению геоэлектриче-ских моделей, для которых в безразмерных переменных была проведена серия численных расчетов. Как и следовало ожидать, в большинстве случаев закон сохранения энергии | Q ^{e, h}|<1 выполнялся. Тем не менее, в работе [Савин, Израильский, 1991] была рассмотрена модель, в которой для электрической моды имеет место обратное неравенство | Q ^h|>1. Однако вопрос с магнитной модой до сих пор оставался открытым.

Рассмотрим трехслойную модель (1), в первом приближении отвечающую геоэлектрическому разрезу в п. Волчинка [Никифоров и др., 1983]: σ 2 /σ 1 =0.1, σ 3 /σ 1 =1, h 2 / h 1 =1. Расчеты производились при r = R /(ωµσ)=10^–3, безразмерная величина скин-слоя 5 = 2/ ( mug ) / h = 10, величина i = J /(ωµσ) изменялась от 0.5 до 1.2, частота ω=0.1 Гц.

Анализировалось поведение функции | Q ^h| в зависимости от параметра i . На рис. 1 приведен график этой функции, рассчитанной на подошве 1-го слоя при z = h –0. Видно, что в малой окрестности точки i =1 коэффициент отражения магнитной моды имеет острый пик, превышающий единицу, | Q ^h( i =1)|=1.14.

Авторы рассматривают еще одну трехслойную модель (2) с параметрами σ₂/σ₁=10, h ₂/ h ₁=1, σ₃/σ₁=1, δ=10, ω=0.1, в которой функции | Q ^e| (рис. 2) и | Q ^h| (рис. 3), рассчитанные на подошве 1-го слоя, также больше единицы, | Q ^e( i =1.01)=1.42, | Q ^h( i =1.96)|=1.28.

Анализ графиков с учетом результатов расчетов электрической моды в модели (1) [Савин, Израильский, 1991] показывает, что при отражении от поверхности раздела проводник–диэлектрик функция | Q ^e| имеет широкий выброс, а функция | Q ^h| — узкий. При отражении от поверхности диэлектрик–проводник ситуация прямо противоположная.

Объяснение случая с Re S z <  0 можно дать с помощью (13) и хорошо известных свойств парциальных импедансов неоднородных плоских волн.

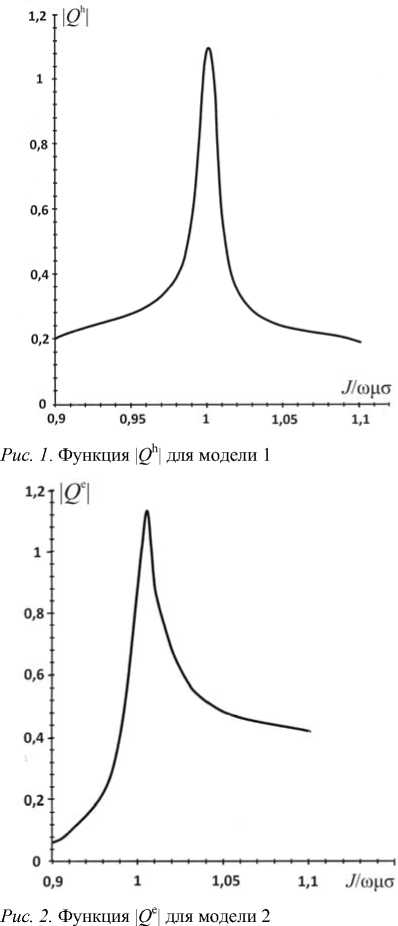
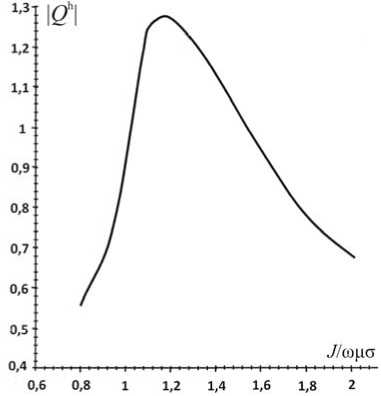
Рис. 3 . Функция | Q ^h | для модели 2

ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ

Мы не можем утверждать, что коэффициент отражения уходит в запредельную область, а вертикальные потоки энергии становятся отрицательными для произвольных слоистых структур — это заведомо не так. Специфика рассмотренных нами трехслойных геоэлектрических моделей, применяемых для регионов Сахалина [Никифоров, 1985], Камчатки [Мороз, 1991] и других, состоит в том, что первый и второй слои имеют примерно одинаковую мощность, первый и третий — одинаковую проводимость, а проводимость второго слоя примерно на порядок меньше (модель 1) / больше (модель 2) проводимости первого. Подобный класс слоистых структур можно было бы назвать резонансными моделями.

Попытаемся дать объяснение полученным результатам как с точки зрения бесконечной энергии неоднородной плоской волны, так и с точки зрения резонанса волна – система слоев.

Если предположить, что энергия волны конечна, из условия | Q |>1 на всей поверхности z =0 следует, что энергия W отр отраженной волны больше энергии W пад падающей, так как W отр =| Q |² W пад . Это противоречит закону сохранения энергии. Однако, поскольку энергия неоднородной плоской волны равна бесконечности на одной из полуосей (например, при х →–∞ и β x >0 А ~exp[ i (α x + i β x ) x ]→∞, W ~| A |²), противоречия нет, так как сравниваются бесконечные величины.

Если же считать, что МТ-поле изменяется лишь на конечном участке земной коры, как это и предполагает модель Четаева, условие W пад > W отр не означает, что для этого участка закон сохранения энергии не выполняется. В самом деле, если ограничить окрестность точки наблюдения (объем V ) некоторой замкнутой поверхностью Σ, приток энергии внутрь этой поверхности может идти не только сверху, но и снизу, и сбоку (см. вышеприведенные выдержки из [Фейнман и др., 1977], т. е. из достаточно удаленных областей вне рассматриваемого участка, где энергия плоской волны достаточно велика. Тогда нужно предположить, что вектор Пойн-тинга S изменяет свое направление, что обеспечивает приток энергии внутрь объема V .

Перейдем к резонансной интерпретации. По-видимому, при | Q ^e,h|>1 мы находимся в области параметров геоэлектрических слоев, близких к значениям, отвечающим собственным частотам системы слоев. При приближении к резонансу величина Q должна неограниченно расти.

В этой связи интересно сравнить ситуацию, возникающую при отражении звуковой волны от упругой пластинки, помещенной в жидкость [Брехов-ских, 1957]. Рассматриваются свободные волны в пластинке, т. е. такие волны, которые могут существовать при амплитуде падающей волны, равной нулю (без внешнего возбуждения). «При стремлении амплитуды падающей волны к нулю, — пишет Л.М. Бреховских, — амплитуды отраженной и прошедшей волн остаются конечными и коэффициент отражения может принимать любые наперед заданные значения». Прослеживается аналогия между свободными волнами в пластинке и поверхностными волнами (волны Рэлея) на границе твердого тела и жидкости. «В этом случае будет иметь место волновой процесс, распространяющийся вдоль границы без падающей волны, т. е. будем иметь случай поверхностной волны» (Л.М. Бреховских).

В нашей постановке рассматривается также поверхностная, но не акустическая, а электромагнитная волна с комплексными пространственными частотами. При этом параметры обнаруженной трехслойной модели 1 (ρ 2 =10ρ 1(3) ), отвечающей аномальным энергетическим характеристикам поля, можно соотнести с пластинкой, упругие свойства которой отличны от свойств выше и ниже расположенной жидкости. На рис. 1 видно, что здесь имеет место узкий выброс функции Q ^h, который можно соотнести с резонансным пиком, в то время как выброс функции Q ^e гораздо более пологий. В этом случае, т. е. при отражении от поверхности раздела проводник–диэлектрик вступает в резонанс с моделью 1 магнитная мода. Узкий выброс функции Q ^е (рис. 2) при отражении от границы диэлектрик– проводник свидетельствует о том, что в резонанс с моделью 2 вступает электрическая мода.

Чтобы далее пояснить полученные результаты, вспомним [Четаев, 1985], что процессы распространения электромагнитных полей в слоистых средах имеют глубокую аналогию с распространением волн в одномерно-передаточных линиях из двух проводников, по которым текут токи в противоположных направлениях. При этом Е-моде отвечает последовательный импеданс, а Н-моде — шунтовой адмитанс. Ситуацию с резонансом в обоих случаях нетрудно выяснить читателю самостоятельно, поскольку из-за громоздкости выкладок изложение этого вопроса в данной статье нецелесообразно.

ЗАКЛЮЧЕНИЕ

Настоящая работа ставила своей целью возродить интерес исследователей к модели Четаева, отличающейся удивительной простотой и изяществом. К сожалению, в последние годы она стала незаслуженно забываться. Авторы сделали попытку раскрытия новых возможностей этой модели для изучения так называемых энергетических аномалий МТ-поля, не объясняемых в рамках традиционной модели Тихонова–Каньяра. Благодаря математическому эксперименту удалось найти объяснение кажущемуся нарушению закона сохранения естественного электромагнитного поля Земли в диапазоне Рс3 геомагнитных пульсаций исключительно структурными свойствами электрической и магнитной мод, суперпозиция которых отвечает первичному (полному) МТ-полю. С учетом ранее полученных в дирекционном анализе результатов появляется возможность интерпретации экспериментально наблюдаемых МТ-полей более широкого класса, чем при традиционном подходе. Свойствами естественного электромагнитного поля, не укладывающимися в прокрустово ложе модели однородной плоской волны, но получившими законное право использования при выполнении дирекционных МТЗ, являются горизонтальная неоднородность поля, наблюдающаяся практически повсеместно; экспоненциальное изменение амплитуды Pi2-пульсации [Савин, 1986]; наконец, класс Рс3 геомагнитных пульсаций, обнаруживающих энергетические аномалии. При интерпретации согласно модели Тихонова–Каньяра все вариации МТ-поля с указанными свойствами отбра- сываются. Авторам представляется, что для гео-электрических исследований не воспользоваться широкими перспективами, которые открывает модель Четаева, обогащающая арсенал традиционной интерпретации, было бы непростительной ошибкой.