Новый метод обработки записей сейсмических колебаний, основанный на анализе корреляционных функций флуктуаций амплитуды и фазы Ч. 1. Результаты использования метода в численном модельном эксперименте

Основные принципы, на которых основан предлагаемый здесь метод анализа записей колебательных процессов, были сформулированы в работе [Поляков, Потапов, 2001]. В [Поляков, 2005] этот метод был впервые использован для исследования колебательных режимов магнитного поля Земли. В результате сделан важный вывод: с помощью данного метода можно получать информацию о колебаниях, которую невозможно получить другими традиционными методами, такими как метод спек- трального или спектрально-временного анализа. Было обнаружено, что на участке записи магнитного поля вклад в общее возмущение могут давать сразу три различных магнитосферных резонатора, и определена частота первой гармоники каждого из них. Поскольку этот метод является универсальным, конечной целью данного исследования является попытка использования его для анализа сейсмических записей колебаний земной поверхности.

Рассмотрим участок почти монохроматических колебаний, которые содержат малые по величине случайные изменения амплитуды и фазы. В этом случае спектральная линия участка будет иметь небольшой разброс по частоте, а на записи каждое отдельное колебание по своей форме, амплитуде и периоду немного отличается от всех остальных. Среди колебаний естественного происхождения так выглядят, например, регулярные геомагнитные пульсации Pc1 и Pg. Такой же вид имеет запись любого процесса с высоким уровнем помех после полосовой фильтрации с достаточно узким частотным интервалом. Согласно [Гудзенко, 1961], в радиофизике подобные колебания принято считать периодически нестационарным случайным процессом, и для него справедливо обобщение эргодической теоремы. Это означает, что по всем отдельным колебаниям, которые входят в состав участка записи, мы можем определить одно среднее колебание, которое периодически повторяется от начала и до конца участка. Кроме того, при определении авто- и кросскорреля-ционных функций случайных изменений амплитуды и фазы мы также можем использовать усреднение по ансамблю реализаций, каждая из которых представляет собой отдельное колебание на участке записи. Именно в таком способе определения корреляционных функций заключается главная отличительная особенность предлагаемого здесь метода обработки. Другой особенностью является использование алгоритма практического определения среднего колебания, предложенного в работе [Гудзенко, 1962]. Этот алгоритм лег в основу пакета программных модулей, который был создан в ходе исследований в работах [Поляков, Потапов, 2001], [Поляков, 2005] и состоит из последовательных процедур обработки временных рядов. Порядок выполнения этих процедур и их основные алгоритмы подробно описаны в указанных работах. Кратко перечислим основные этапы обработки.

Исходным является временной ряд цифровых отсчетов x(ti), соответствующий интервалу записи колебательного процесса. После предварительной обработки (устранение выбросов, фильтрация и т. д.) каждое значение x(ti) и время ti становятся безразмерными в результате нормировки соответственно средней амплитудой и средним периодом колебаний в интервале. Для каждого отсчета определяется производная, y(ti)=dx/dt, и точки x(ti), y(ti) наносятся на фазовую поверхность прямоугольных координат (x, y=dx/dt). Каждое отдельное колебание на этой поверхности образует замкнутую траекторию (цикл), при малых флуктуациях не слишком отличающуюся от окружности единичного радиуса. Среднее колебание, или средний цикл, определяется методом последовательных приближений, алгоритм которого подробно описан в [Гудзенко, 1962]. После того как средний цикл установлен, для всех точек x(ti), y(ti) исходных циклов определяется фаза среднего колебания 0i и отклонение вдоль направления нормали от среднего цикла n(0i). Тангенциальные отклонения точек определяются соотношением у(0i)=0i-ti. Физически фаза среднего колебания 0 = mt = 2пt, где и = 2п - средняя частота с учетом нормировки времени. Нормальные и тангенциальные отклонения n и γ соответствуют случайным флуктуациям амплитуды и фазы колебаний. Полученные таким образом значения зависимостей n(0i), у(0i) и их производных по времени dn/dt(0i), dу/dt(0i) позволяют определить для них кросс- и автокорреляционные функции. Конечным продуктом перечисленных процедур обработки являются не сами эти функции, а их алгебраические комбинации, определяемые по формулам:

G(0, т)= (y(0) Y(0 — т)^nn(0)n(0-т)^-

• - (y (0) n (0- т)) nn (0) Y (0- т));

G1 (0, т) = ^(0) Y(0-т)^(y(0)n(0-т))-

• -^ ^0) n (0-т )^ (y (0) Y (0-т));

G2 (0, т) = -/y(0) y(0-т))(y(0)n(0-т)) + / •                 \                                        (1)

+ /y (0) n (0-т)) (y (0) y (0-т)},

где точка над символом означает производную по фазе 0 , угловые скобки - усреднение по ансамблю отдельных колебаний, а τ – сдвиг фазы. Зависимость этих функций от фазы 0 должна быть периодической, поскольку они определяются на интервале от 0 до 2π. Следовательно эту зависимость можно представить в виде ряда Фурье, коэффициенты которого зависят только от τ. Из работы [Поляков, Потапов, 2001] следует, что для функций (1) более важной является зависимость от сдвига фазы. Поэтому в дальнейшем мы будем изучать свойства коэффициента только одной, нулевой гармоники ряда Фурье, который, по существу, совпадает со средним по фазе 0 значением каждой из функций. Именно эти, зависящие только от τ средние значения, для простоты будем называть корреляционными функциями флуктуаций амплитуды и фазы (КФАФ).

Оказалось [Поляков, Потапов, 2001; Поляков, 2005], что КФАФ обладают очень любопытным и важным для исследования колебательных систем свойством. Если колебание является результатом наблюдения эволюции волнового процесса в какой-нибудь точке резонатора, то зависимость КФАФ от τ будет иметь вид последовательности максимумов (пиков), следующих друг за другом через равные интервалы. Для объяснения этого свойства в [Поляков, Потапов, 2001] рассмотрена модель простейшего одномерного резонатора с «закрепленными» концами, колебания в котором возбуждаются источником волнового типа. Для колебаний в точке, находящейся вблизи одного из концов, удалось получить аналитические соотношения для КФАФ в приближении, когда частота источника не сильно отличается от одной из собственных частот резонатора. Оказалось, что зависимость КФАФ от τ определяется рядами гармонических функций синус и косинус кратного аргумента x =(ω₁/ω)τ, где ω, ω₁ – частота источника и частота первой гармоники резонатора.

Суммирование производится по номерам гармоник. Результатом суммирования являются чередующиеся через равные интервалы пики, а положение пика на оси τ определяется условием для аргумента x =2π n :

т n = 2п N —, (2) ω₁

где N – номер пика. Отсюда интервал между двумя соседними пиками

Д = т N + 1 - т N = 2п —. (3) ω₁

Полученный результат напоминает принцип действия дифракционной решетки. Действительно, угловое распределение интенсивности света после прохождения через дифракционную решетку также определяется рядами гармонических функций кратного аргумента, только суммирование производится по номерам щелей решетки. Из условия, накладываемого на аргумент, следует известное условие для углового положения пика интенсивности или спектральной линии, аналогичное (2). Обнаруженное сходство дает нам основание считать метод КФАФ аналогом дифракционной решетки, только, в отличие от решетки, он представляет собой не какое-то физическое устройство, а пакет программных модулей. На входе мы имеем запись исследуемых колебаний, а на выходе получаем последовательность пиков (линий) на зависимостях КФАФ от τ. По пикам можно определить интервал Δ, частота ω легко определяется по исходным колебаниям, поскольку в вынужденных колебаниях частота источника совпадает с частотой колебаний. Значит соотношение (3) дает возможность для определения ω 1 . Таким образом, если дифракционная решетка предназначена для определения длины волны света, то с помощью метода КФАФ мы можем экспериментально измерять частоту первой гармоники резонатора, которая не зависит от эволюции волновых процессов, а определяется только характеристиками среды, такими, как размер резонатора и волновая скорость.

Рассмотренная выше аналогия метода КФАФ с измерительным прибором оказывается весьма функциональной еще и потому, что позволяет указать направление для дальнейших исследований. Прежде всего следует выяснить, что именно мы собираемся измерять этим прибором при обработке упругих колебаний в среде, состоящей из совокупности плоских слоев. Кроме того, совершенно необходимо провести испытания прибора на реальных сейсмических колебаниях. Если окажется, что зависимости КФАФ от τ для реальных колебаний не выглядят как последовательности пиков и какие-либо измерения невозможны, все остальное теряет смысл.

В данной работе для выявления особенностей пиков КФАФ, также как в работе [Поляков, 2005], используется схема численного модельного эксперимента, а не аналитические расчеты этих функций, как это было сделано в [Поляков, Потапов, 2001] для одномерного резонатора. Суть схемы заключается в следующем. Сначала выбираем модель среды (двухмерный прямоугольный слой или совокупность нескольких слоев) и задаем дифференциальные уравнения для смещения точек среды. Затем с помощью подходящей разностной схемы эти уравнения решаются численно, и для разных точек среды получаются временные участки записи колебательного процесса. Каждый из них подается на вход обрабатывающей программы, на выходе которой получаются зависимости КФАФ от τ, которые имеют вид последовательности пиков. Меняя параметры среды и уравнений и проделывая вычисления заново, можно выяснить, от чего зависят характеристики пиков, и эмпирически получить формулы, подобные (2), (3).

Далее в работе метод КФАФ используется для обработки записей сейсмических колебаний на станции Талая (Восточный Саян). Здесь опытным путем убедительно показана применимость метода для реальных колебаний. При этом измерения времени пробега P- и S-волн вертикально вниз от очага землетрясения до отражающей поверхности оказались также весьма достоверными.

Результаты численного эксперимента

Моделью среды будем считать прямоугольную пластину упругого вещества. Размеры пластины вдоль координатных осей OX и OZ обозначим соответственно l x , l z . Ось OZ полагаем направленной вертикально вниз с началом на верхней поверхности пластины. Размер вдоль оси OY считаем неограниченным, т. е. будем рассматривать двумерную модель, когда характеристики вещества и смещения точек не зависят от координаты y. Сначала рассмотрим свойства КФАФ для P–SV-волнового процесса, который представляет собой суперпозицию продольно поляризованной Р-волны и поперечо поляризованной в плоскости XZ S-волны. В этом случае поляризация смещения точек среды должна быть u = ( u x , 0, u z ) . Уравнения для смещений u_x и u z вдоль осей OX и OZ имеют вид [Ландау, Лившиц, 1987; Аки, Ричардс, 1983; Буллен, 1966]

д u

д ² u_r    , д u_r    д Г/, -_t,₂xU u_r

+ 5    = Ч + 2 Ч ²

д t²       д t    д x ⁽ 1       ² ) д x

+

д x

_д_ ^Г 2 Э^ ) 2 Гу 2 ^дЦХ L 2 Гу 2 ^дЦх Y

I                   ч                            I                   ч                            I                   ч                          ;

д x Г    д z ) д z Г     д z ) д z Г    д x )

yz-+5 У=дк I(Ч2+24 Ут I+

д L ^uu, ) д Г ₂д u, ) д Г ₂д u )

+    Ч ²      + Ч ²      + Ч ² z- ;

д z Г ¹   д x )   д x Г ^z   д z )  д x Г ^z   д x У

Ч =

,

где ρ – плотность вещества, λ и µ – постоянные Ламе, характеризующие упругие свойства вещества, δ – коэффициент затухания. Слагаемые, пропорциональные δ, введены в уравнения искусственно и обуславливают временное затухание колебаний в точ- ках среды, естественное для любого реального процесса. Будем считать, что боковые и нижняя поверхности слоя имеют граничные условия, соответствующие «закрепленным» концам, а верхняя поверхность «свободна», т. е. напряжение вдоль OX и OZ на ней равно нулю [Аки, Ричардс, 1983]:

u x (0, z )= u x ( l x , z )= u z (0, z )= u z ( l x , z )=0 при 0≤ z ≤ l z ;

(V + х- ^ (x,0) = -V dx (x,o);

’—~ ( x -0 ) = -^ ( x -0 ) при0-^ l x . (5) о z a x

Источником, возбуждающим волны в слое, будем считать часть свободной поверхности, на которой для u x или u z задаются колебания с распределением по x , соответствующим стоячей волне. Например:

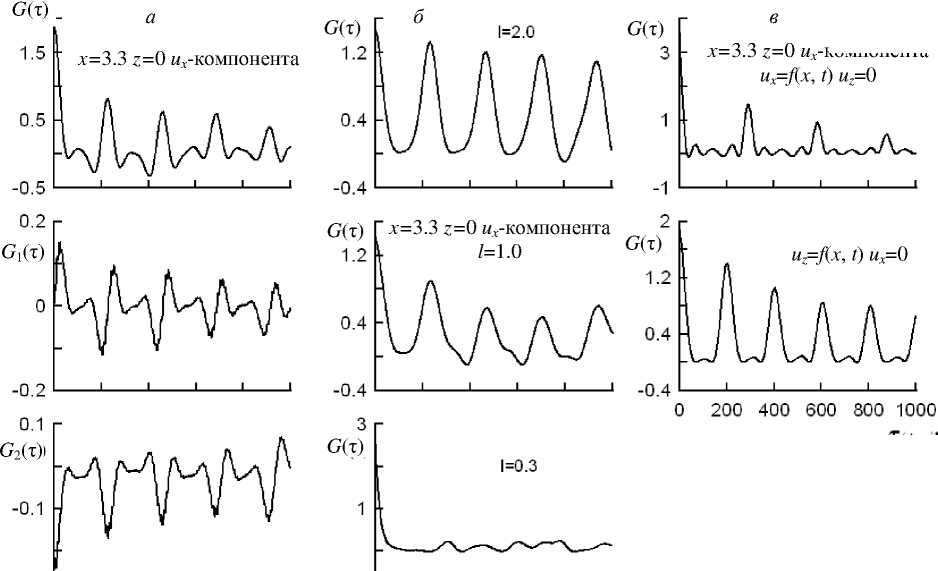
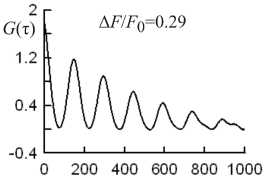
ux (x, 0) = f (x, t) = A sin ^|x^j[sin (tot) + F (t)] -uz (x- 0) = 0 при 0

Для численного решения (4), (5) с выбранной конфигурацией источника была использована явная разностная схема (см. [Аки, Ричардс, 1983], метод конечных разностей) и соответствующая этой схеме последовательность алгоритмов вычислений. Задавая шаги пространственно-временной сетки и значения параметров lx, lz, V1, V2, δ, A, ω, l, мы в результате вычислений получаем временные зависимости для компонент смещения ux(t) и uz(t) в любой точке слоя. Эти зависимости представляют собой квази-монохроматические колебания, так как источник содержит одну частоту. Мы будем рассматривать колебания только в тех точках, которые находятся на верхней свободной поверхности, поскольку это больше соответствует реальным сейсмическим колебаниям. Кроме того, для большего приближения к реальности время действия источника выбиралось таким образом, чтобы при заданных значениях lx, V1, V2 волна вдоль оси OX не успевала пройти путь lx и отразиться в обратном направлении. При этом волну горизонтального направления следует считать бегущей, а слой – волноводом.

После того как численно определены зависимости ux(t), uz(t) в разных точках, в каждой из них выделяется участок, включающий в себя примерно 100 отдельных колебаний. На последнем этапе участок обрабатывается упомянутыми ранее процедурами в определенной последовательности, результатом чего является определение зависимости от сдвига фа- зы τ корреляционных функций флуктуаций амплитуды и фазы (1). На рис. 1, а приведен пример такой зависимости для всех трех функций. На рисунке указаны координаты точки наблюдения колебаний и компоненты смещения, для которых получены графики. Единицей измерения длины является толщина слоя. Координата X отсчитывается от начала слоя. Значения функций являются безразмерными величинами. Сдвиг фазы τ измеряется в радианах. Единица измерения (масштаб) по оси абсцисс для этих графиков и для всех приводимых в дальнейшем равна π/10. Как видно из рис. 1, а, характерной особенностью для G(τ) является наличие дополнительного пика между соседними главными пиками. Иногда, в зависимости от выбранного участка или точки наблюдения колебаний, высота этих пиков может оказаться более значительной и сравнимой с высотой основных пиков. Функция G1(τ) характерна тем, что не похожа на последовательность пиков, а выглядит скорее как последовательность разрывов, аналогично функции тангенс. Зависимость G2(τ) представляет собой последовательность пиков, повернутых вниз. Перечисленные особенности КФАФ, как оказалось, в дальнейшем сыграют важную роль при сравнении с КФАФ реальных сейсмических колебаний. Однако на данном этапе нам необходимо выяснить, каким образом перечисленные выше параметры модели влияют на положение пиков и на интервал между соседними пиками Δ. Поэтому в дальнейшем мы будем использовать только функцию G(τ) как наиболее показательную относительно пиков. Меняя значения параметров модели и заново повторяя процедуры вычислений вплоть до определения Δ, удалось выявить ряд интересных закономерностей.

Оказалось, что при одних и тех же параметрах модели интервал Δ и положение пиков одинаковы для всех точек наблюдения колебаний и для обоих компонент смещения. При этом отчетливость наблюдаемых пиков зависит от расстояния между точкой и источником. На небольших расстояниях в КФАФ наблюдаются очень четко выраженные пики. При увеличении расстояния пики становятся искаженными и меньшими по высоте. В некоторых точках они просто исчезают, и функция G(τ) становится похожей на корреляционную функцию обычного фильтрованного белого шума. Однако при дальнейшем увеличении расстояния до источника пики появляются снова и становятся весьма отчетливыми. Получается, что на свободной поверхности вокруг источника существуют зоны, в которых для КФАФ наблюдаются отчетливые пики, и зоны, в которых их просто не существует.

Аналогичное влияние на четкость пиков имеет размер источника l. На рис. 1, б приведены три графика G(τ), полученные при одинаковых параметрах модели в одной и той же точке свободной поверхности, но с различными значениями l. Координаты точки и размер источника указаны в единицах толщины слоя lz. Видно, что при l=lz пики наблюдаются, но уже заметно искажены, а при l=0.3lz их просто нет. Отсюда следует, что точечный источник колебаний не создает условий для образования пиков в КФАФ.

компонента

Т(*7Е/10)

-I -------------1------------1-------------1-------------1-------------1

О 200 400 600 800 1000

-О 3 ----------1----------1---------1----------1----------1

О 200 400 600 800 1000

Т( *№10)

Т(*л/10)

Рис. 1. Зависимость корреляционных функций флуктуаций амплитуды и фазы от фазового сдвига τ для модели волноводного распространения P- и S-волн в слое упругого вещества. Зависимости от τ для всех трех КФАФ (а); влияние на отчетливость пиков функции G(τ) размера источника l (б); зависимость положения пиков КФАФ на оси τ от поляризации колебаний в источнике (в).

Пики начинают появляться только при l≥lz, когда направление распространения излучаемой источником волны, без учета эффектов на краях, почти совпадает с направлением поперечной к слою оси OZ. Это значит, что условие квазипоперечности волны является одним из основных условий для возникновения пиков КФАФ колебаний точек свободной поверхности слоя.

Другой особенностью КФАФ оказалось то, что наблюдаемые пики могут быть двух типов. На рис. 1, в приведены графики G(τ), которые отличаются друг от друга только поляризацией колебаний в источнике. Для верхнего графика смещение точек в источнике направленно вдоль оси OX, а для нижнего – вдоль оси OZ. Зависимость от координаты и времени колебаний в источнике определяется функцией f(x, t) и одинакова в обоих случаях. Отчетливо видно, что положения всех пиков на оси τ для обоих графиков существенно отличаются друг от друга. Интервалы между соседними пиками Δ также различны. Необходимо отметить, что при одной и той же поляризации в источнике во всех точках поверхности наблюдаются пики только одного типа. При смешанной поляризации, когда ux=uz=f(x, t), в разных точках могут наблюдаться пики только или одного или другого типа. На одном графике G(τ) оба типа пиков одновременно присутствовать не могут.

Наличие двух типов пиков КФАФ легко объяснить, если учесть, что исходные уравнения (4) включают в себя одновременно P- и S-волны. При этом каждой волне должен соответствовать свой тип пиков. Поскольку скорости этих волн разные, то интервал Δ будет отличаться у P- и S-пиков. Оказалось, что Δ в обоих случаях зависит от ω, lz, V2, а от V1 зависимость имеет место только для P-пиков. Характер обнаруженных зависимостей позволяет сконструировать эмпирические формулы для обоих типов пиков. Они имеют вид

ωl        2l                ωl2

А = 2п —— = 2п —— или А = 2п —- = 2п ——; πVP     TVP           πVS

Vp = VV + 2V2 = . /^. Vs = v2 = , £,(6)

ρρ где VP, VS – скорости P- и S-волн, T – период колебаний источника, который совпадает с периодом обрабатываемых колебаний. Для удобства представим (6) в виде t                2l2

А= 2П — . tA = tAP = "ТГ" или tA = tAS =    .

T           VP

Время t_AP и t_AS есть удвоенное время пробега (туда и обратно) поперек слоя для P- и S-волн. Интересно, что полученные формулы для упругих волн вновь, также как в [Поляков, 2005], оказались подобны соотношению (3) для одномерного резонатора, поскольку tAP и tAS можно рассматривать как периоды первой гармоники стоячих волн поперек слоя.

Следующая особенность для пиков КФАФ связана с наличием неоднородности вдоль слоя. Рассмотрим ситуацию, когда скорости P- и S-волн зависят от координаты x. Для простоты будем считать, что V1=0, а скорость V2 меняется скачком

в точке x=x0:

V2 ( ^ ) =

0 < x< x₀

x0 < x < lx.

На рис. 2, а приведены графики функции G(τ) для рассматриваемого случая. Точка наблюдения колебаний верхнего графика находится, как и источник, в области со значениями скорости V'_ , точка наблюдения среднего находится точно на границе между областями, и нижний график получен для точки из области со скоростью V". Из рисунка видно, что интервал Δ во всех точках одинаков. Это значительно уточняет смысл tA. Получается, что мы не можем считать это время временем пробега поперек слоя под точкой наблюдения колебаний, хотя вначале предполагалось, что это должно быть именно так. Пики на рис. 2, а относятся к S-типу, и для них должна быть справедлива вторая формула (6). Оказалось, что интервал Δ, вычисленный по этой формуле, совпадает с интервалом А, наблюдаемым на графиках, если V₂= V. Следовательно, время пробега tA должно определяться скоростью волн под источником. Полученный вывод подтверждается при анализе ситуации с монотонной зависимостью V2(x). В этом случае точно также интервал между соседними пиками во всех точках одинаков и определяется временем пробега t_A P- или S-волн поперек слоя в области источника.

Еще одна особенность пиков КФАФ обнаружилась после того, как источник был перемещен вдоль оси OZ. В этом случае источником по-прежнему остается плоская поверхность, параллельная слою, но расположенная не на верхней свободной поверхности, а внутри слоя на некоторой глубине. Оказалось, что при таком смещении интервал Δ для точек на верхней свободной поверхности слоя становится меньше. Причем в эмпирической формуле (6) это уменьшение связано с изменением размера l_z. Отсюда следует, что в формуле (6) время t_A определяется временем прохождения упругих волн вертикально вниз не от верхней до нижней границы слоя, а от источника до нижней границы. Кроме этого, оказалось, что если точка наблюдения колебаний находится в области проекции источника на верхнюю поверхность слоя, то время tA для нее совпадает со временем движения волны от источника до верхней границы. Однако если точка смещается за пределы этой области хотя бы на несколько шагов пространственной сетки, то время tA определяется временем движения от источника до нижней границы слоя.

Далее рассмотрим влияние неоднородности среды поперек слоя. Будем считать, что скорость V₂ вдоль координаты z меняется от значения V‘ до V"

ластью толщиной Δz. На рис. 2, б приведены графики функции G(τ), полученные с использованием такой модели. На каждом графике указаны координаты точек (в единицах lz), компоненты смещения, по колебаниям которых определены эти функции и типы наблюдаемых пиков. Источник в обоих случаях расположен на свободной поверхности верхнего слоя и имеет размер 2lz. Координаты границы между слоями одинаковы, z0=0.3lz, однако ширина переходной области в верхнем графике Δz=0.3lz существенно больше, чем в нижнем, Δz=0.03lz. Оказалось, что интервал между пиками Δ, наблюдаемый на первом графике, совпадает с вычисленным по формуле (7) только в том случае, если время tA определяется соотношением

. _ ^{2 z}0 , ^{2 (}lz ^z0 ) _ ^{2 z}0 , ^{2 (1} A = V' V" = V' ’

2           2           S2

V₂

lz - z 0 )

VS2

.

Получается, что tA совпадает с полным временем пробега S-волны (туда и обратно) в поперечном направлении для обоих слоев вместе. Для нижнего графика наблюдаемый интервал Δ совпадает с вычисленным по эмпирической формуле, если

2z₀    2z₀

A V2v; V^

в окрестности точки z = z0:

V2 (z ) =

V

0 < z< z₀- Az /2

= <

V" + V‘

+

V"

V₂

-

V'

V₂

Az

(z - z 0 )

T r*

^V2 ^,

z₀- Az /2 < z< z₀+ Az /2 z₀+ Az /2 < z< l_z.

Это означает, что вместо одного слоя рассматривается двухслойная модель среды с переходной об-

В этом случае t_A определяется временем пробега P-волны только одного верхнего слоя. Полученное отличие объясняется тем, что в первом случае волна проходит через плавную границу между слоями без существенного отражения и полностью отражается от нижней границы второго слоя. Во втором случае граница между слоями является более резкой, и почти полное отражение происходит от этой границы. При этом интервал между соседними пиками КФАФ четко отслеживает время движения волны до той поверхности, от которой происходит полное отражение. Рисунок 2, в демонстрирует особенности влияния на интервал Δ частоты источника ω для модели (8) с резкой границей между слоями Δz=0.03lz. Наблюдаемые на всех графиках пики относятся к S-типу. На верхнем графике, согласно эмпирической формуле (7), время tA для интервала Δ определяется соотношением (9), т. е. соответствует времени пробега обоих слоев. На среднем графике интервал Δ увеличивается с возрастанием частоты ω. Это значит, что время tA в (7) не меняется и увеличение связано с изменением T. Однако на нижнем графике с увеличением ω интервал Δ не увеличивается, а уменьшается. При этом оказывается, что время tA в (7) также существенно уменьшилось и стало соответствовать времени прохождения волны только одного верхнего слоя. Эта особенность изменения интервала Δ может означать только то, что при значениях частоты источника ω=1.1π, ω=2.0π отражение волн происходит от нижней границы второго слоя, а при частоте ω=3.0π волны отражаются от границы между слоями.

Последний вопрос, который необходимо прояснить, относится к проблеме применимости метода КФАФ для обработки колебаний естественного происхождения. Необходимо выяснить, какое влияние

Рис. 2. Зависимости КФАФ от τ для модели слоя упругого вещества с учетом продольной и поперечной неоднородностей. Влияние продольной неоднородности на положение пиков КФАФ в точках с разными координатами (а); влияние толщины переходной области между слоями на положение пиков КФАФ (б); зависимость положения пиков КФАФ от частоты источника в модели с двумя слоями (в).

оказывает фильтрация исходного колебания на конечный продукт обрабатывающей программы – корреляционные функции (1). Как уже было отмечено в предыдущем разделе, исходные колебания должны быть квазимонохроматичными. Это значит, что они должны не очень отличаться от синусоиды в течение большого промежутка времени, не содержать амплитудных и фазовых сбоев, иметь минимальный уровень внешнего шума. Среди колебаний естественного происхождения, например для геомагнитных пульсаций, такие события встречаются довольно редко, а записи сейсмических колебаний этим критериям заведомо не удовлетворяют. Получается, что предлагаемый здесь метод обработки не может быть использован для этих колебаний. Однако известно, что любой сколько угодно зашумленный сигнал превращается в почти монохроматический, если на него подействовать фильтром с узкой частотной полосой пропускания. И чем уже полоса пропускания, тем «монохроматичнее» становится сигнал. Возникает вопрос: повлияет ли такая фильтрация исходных колебаний на периодическую структуру пиков КФАФ? Из общих соображений следует, что корреляционные функции должны меняться, поскольку фильтрация приводит к искажению случайных флуктуаций амплитуды и фазы. Однако оказалось, что это не так. Для проверки были использованы колебания ux-компоненты смещения, рассчитанные в рамках однослойной модели с повышенным уровнем шума в источнике, в точке свободной поверхности с координатами x=10l_z, z=0.

Фильтрация осуществлялась фильтром Марме [Marmet, 1979], немного модифицированным для наших целей. Характеристиками фильтра является центральная частота F0 и ширина полосы пропускания ΔF. На рис. 3 представлены графики функции G(τ), полученные после фильтрации колебаний компоненты смещения u_x при различных значениях относительной ширины полосы пропускания фильтра ΔF/F₀. Поскольку в спектральном составе колебаний u_x содержится одна частота, то F₀ остается постоянной, и все отличия графиков связаны с изменением ширины ΔF. Сравнение графиков убедительно показывает, что структура пиков КФАФ не только не искажается при сужении полосы фильтрации, но даже в определенном смысле улучшается. Главные пики становятся более отчетливыми. Положение пиков на горизонтальной оси и интервал Δ между соседними пиками абсолютно не меняется даже при уменьшении ширины полосы пропускания более чем в 2 раза. Единственное отличие при этом состоит в небольшом увеличении ширины пиков. Эту особенность можно рассматривать как дополнительное подтверждение упомянутой ранее аналогии метода КФАФ с дифракционной решеткой. Действительно, если считать, что зависимость КФАФ от τ определяется суммированием гармонических функций по номерам гармоник стоячей волны поперек слоя, то фильтрация колебаний ведет к удалению некоторой части гармоник из спектрального состава и уменьшению числа слагаемых в сумме. При этом пики КФАФ остаются на месте, увеличивается только их

3 г

С(т)

AF/F0=0.66

VJVJVjV^

-1

2.5

-0.5

T( *ти/10)

Рис. 3. Влияние полосовой фильтрации исходных колебаний на ширину и положение пиков КФАФ.

их ширина. То же самое наблюдается, если в дифракционной решетке уменьшить число щелей, по номерам которых производится суммирование. Известно , что в этом случае спектральные линии точно также становятся шире, не меняя своего углового положения.

Все свойства и особенности корреляционных функций флуктуаций амплитуды и фазы, описанные выше, относятся к P–SV-волнам. Важно то, что наблюдаемые в КФАФ пики подразделяются на два типа, каждый из которых соответствует своему типу волн. При этом характер изменения параметров пиков, в зависимости от изменения характеристик модели, для обоих типов абсолютно одинаков. Кроме P–SV-волн с поперечной поляризацией в плоскости XZ, в упругой среде могут независимо существовать SH-волны с поляризацией вдоль оси Y. Они имеют одинаковую с SV-волнами скорость и отличаются от них только направлением смещения точек среды при колебаниях. Поэтому совершенно очевидно, что SH-волны должны приводить к возникновению таких пиков в КФАФ, которые относятся к уже рассмотренному нами ранее S-типу пиков. Кроме того, на свободной поверхности упругой среды могут образовываться волны Рэлея и Лява. В нашей модели, в силу накладываемых условий, эти поверхностные волны должны быть бегущими. Бегущие волны отличаются от стоячих тем, что расстояние между точками отражения стремится к бесконечности. Значит, если эти волны могут приводить к образованию пиков в КФАФ, характерный размер для них в формуле (6) должен быть равен бесконечности, и интервал между соседними пиками Δ→∞. Получается, что в КФАФ для волн Рэлея и Лява невозможно обнаружить последовательность пиков, поскольку положение даже первого пика на оси абсцисс графика соответствует бесконечности.

Заключение

Кратко сформулируем основные результаты.

• 1.    Для колебаний компонент смещения в разных точках свободной поверхности корреляционные функции флуктуаций амплитуды и фазы имеют вид периодической последовательности пиков только в том случае, если источник имеет вид плоской поверхности, параллельной слою, и размер источника сравним с поперечным размером волновода.

• 2.    Положения пиков на горизонтальной оси графиков зависимости КФАФ от сдвига фазы τ одинаковы во всех точках свободной поверхности. Интервал между двумя соседними пиками Δ определяется по эмпирической формуле (7), в которой время tA определяется временем движения P- или S-волн вертикально вниз от источника до поверхности, от которой происходит полное отражение этих волн.

• 3.    Узкополосная фильтрация исходного колебания компоненты смещения не приводит к искажениям в зависимостях КФАФ от τ, т. е. положение пиков и интервал Δ после фильтрации не меняются.