Новый метод обработки записей сейсмических колебаний, основанный на анализе корреляционных функций флуктуаций амплитуды и фазы Ч. 2. Использование метода КФАФ для анализа структуры оболочек Земли

В этом разделе мы попытаемся применить опи санную выше методику обработки сигналов , конеч ным продуктом которой являются корреляционные функции флуктуаций амплитуды и фазы ( КФАФ ), для исследования реальных сейсмических колебаний . Основной целью при этом является ответ на вопрос : позволит ли этот метод , в совокупности с результа тами настоящего раздела , получить новую экспери ментальную информацию о структуре земных слоев и отражающих волны поверхностей ?

Для анализа нами были выбраны записи всех компонентов смещения точки земной поверхности на ст. Талая (Восточный Саян) от девяти различных удаленных источников землетрясений. Каждая такая запись имеет продолжительность 1 ч с момента начала землетрясения. Данные о смещениях выставлены на сайте и представляют собой последовательность цифровых отсчетов с временным интервалом 1 с между ними.

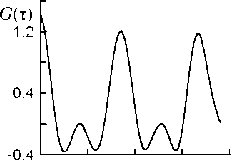
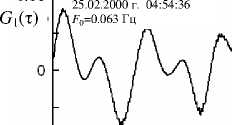
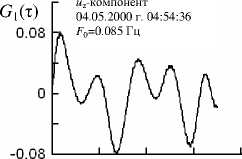
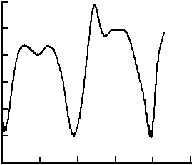
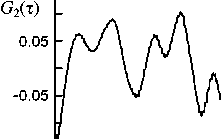
На предварительном этапе обработки для каждой записи компонента смещения путем фильтрации выделяется соответствующий интервал записи колебательного процесса. Значение ширины частотной полосы пропускания фильтра ΔF и особенности амплитудно-частотной характеристики при этом не имеют особого значения. Главное, чтобы после фильтрации колебания получались почти монохроматическими и удовлетворяли упомянутым ранее критериям. Меняя центральную частоту фильтра F0, мы можем выделять из общей записи квазимонохроматиче-ские колебания на разной частоте. После фильтрации из всего часового интервала выделяются отдельные участки колебаний, которые служат исходными данными для следующего этапа обработки. Конечным продуктом этого этапа являются зависимости КФАФ от сдвига фазы τ, соответствующие каждому отдельному участку. Первые же опыты обработки по указанной схеме позволили обнаружить любопытное явление. Оказалось, что для некоторых участков сейсмических колебаний КФАФ по характеру изменений очень похожи на те корреляционные функции, которые мы получали в модельном эксперименте. На рис. 1 приведены примеры зависимостей КФАФ от τ для таких случаев. На каждом из них указана компонента смещения, дата и время начала участка колебаний и значение частоты F0 при фильтрации. Сравнение этих графиков с рис. 1, а части 1 данного исследования обнаруживает абсолютное подобие. Действительно, функция G(τ) в левом столбце, так же как на рис. 1, а, имеет отчетливые главные пики и небольшие по высоте дополнительные пики. В правом столбце дополнительные пики существенно больше по высоте, и эта особенность также отмечалась в модельном эксперименте. Функция G1(τ), так же как на рис. 1, а, имеет вид периодической последовательности разрывов, особенно это заметно в центральном столбце графиков. Функция G2(τ) во всех случаях имеет точно такой же вид отчетливых пиков, перевернутых вниз. Очевидно, что такое четкое подобие функций невозможно объяснить за счет обычного случайного совпадения, поскольку в каждом случае подобны не одна, а сразу три функции. Обнаруженное подобие тем более удивительно, если учесть, что корреляционные функции определяются по случайным флуктуациям амплитуды и фазы, которые, по сути, представляют собой временные ряды случайных чисел. В модельном эксперименте эти числа обусловлены наличием белого шума, который искусственно создается в источнике. Для реальных сейсмических колебаний затруднительно даже сделать предположение о тех процессах, которые приводят к образованию случайных флуктуаций. Значит, априори невозможно рассчитывать на совпадение КФАФ для модельного эксперимента и для реальных колебаний. Именно поэтому обнаруженное выше подобие этих функций является убедительным экспериментальным доказательством того, что в некоторых случаях для сейсмических колебаний выполняется условие для появления пиков в КФАФ, сформулированное в предыдущем разделе. И самое главное, интервал между соседними пиками должен определяться по формуле (7) в части 1 данного исследования.

Сам по себе этот интервал для таких КФАФ , ко торые приведены на рис . 1, измеряется без особых затруднений . Средний период участка колебаний Т при узкополосной фильтрации определяется часто той F 0 . Значит , согласно формуле (7), мы получаем уникальную возможность для экспериментального измерения времени t A :

t

T A

A 2 n '

Согласно выводам первой части работы , это время пробега ( туда и обратно ) P- или S- волны вертикаль но вниз от источника до отражающей поверхности .

0.4

G ( τ )

1.2

G ( τ )

u _z- компонент

18.06.2000 г . 15:08:23      1И

F 0=0.085 Гц --------------1--------------1--------------1--------------1--------------1                         ------------------L--------------1------------------1-----------

u _z- компонент

-0.03

0.04

-0.4

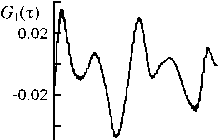
-0.06

0.04

G 2 ( τ )

-0.04

-1

П/V

-0 12 ----------1----------1----------1----------1

О 200 400 600  800

τ × π /10

-0.2

-0.12

-0.15

О 200 400 600 800 1000     0   200  400  600  800

τ × π /10

τ × π /10

Рис . 1. Примеры зависимостей КФАФ от τ для участков реальных сейсмических колебаний .

Источником мы предположительно будем считать очаг землетрясения . Отражающими поверхностями , очевидно , должны служить границы между земны ми оболочками или любые поверхности , способные отражать упругие волны .

Дальнейшие исследования данного раздела работы связаны с использованием формулы (1). Мы попытаемся выяснить, какие новые возможности может давать предлагаемый метод при изучении вопросов, связанных со слоистой структурой Земли. Для этого обработка исходных данных была продолжена по указанной выше схеме. Только в данном случае мы используем КФАФ, полученные на участке фильтрованных колебаний, для измерения интервала Δ и далее с помощью (1) находим tA. Оказалось, однако, что измерение tA подобным образом можно сделать далеко не для каждого участка. Только примерно в 3 % всех проанализированных случаев наблюдаются очень отчетливые пики в КФАФ, такие как представленные на рис. 1. Примерно в 20 % всех случаев пики в КФАФ менее отчетливы, но все-таки позволяют сделать измерение интервала ∆ . Во всех остальных случаях каких-либо пиков в составе корреляционных функций обнаружить просто не удается. Однако это затруднение не помешало нам сформировать массив значений tA на основе довольно большого числа измерений, поскольку обрабатывались записи сразу девяти источников и фильтрация компонент смещения производилась не одним, а несколькими фильтрами с различными значениями центральной частоты. Полученный массив дает возможность для построения функции распределения значений tA, которая представлена на рис. 2. Здесь n – число измеренных значений, попадающих в тот или иной интервал гистограммы, который составляет 5 с, время tA выражается в секундах. Анализ распределения довольно от- четливо показывает, что большинство полученных значений группируются около нескольких характерных времен tA. Номер каждой группы указан на самом рисунке. Тот факт, что всего таких групп получилось четыре, означает, что в структуре земных оболочек должны иметь место две отражающие поверхности, поскольку каждая поверхность должна давать два значения времени пробега tA для P- и S-волн соответственно. Возникает вопрос, какие именно группы относятся к разным типам волн одной и той же отражающей поверхности. Согласно определению времени tA, волны P- и S-типа проходят одинаковый путь вертикально вниз от источника до точки отражения. Значит, отношение времени пробега волн обоих типов должно совпадать с отношением средних значений скорости на пути движения. Согласно сейсмологическим данным [Буллен, 1966; Болт, 1984], отношение скоростей P- и S-волн на глубинах верхней мантии везде почти одинаково и равняется приблизительно 2. Из рис. 2 для характерных времен tA1 группы 1 и tA2 группы 2 получаем tA2 /tA1 ≈ 1.4.

Для групп 1 и 3

t _A3 / t _A1 ≈ 1.9.

Следовательно , одной отражающей поверхностью создаются , скорее всего , группы 1 и 3, поскольку 1.9 гораздо ближе к 2, чем 1.4. При этом время t A в группе 1 определяется временем пробега P- волн , а в группе 3 – временем пробега S- волн . То же самое относится к группам 2 и 4, которые образуются при отражении соответственно P- и S- волн от другой поверхности .

Попытаемся определить , на какой глубине распо ложены выявленные отражающие поверхности . Сред няя скорость P- волны на глубинах верхней мантии , согласно [ Буллен , 1966; Болт , 1984], составляет 8 км / с . Время пробега P- волны до первой и второй поверх -

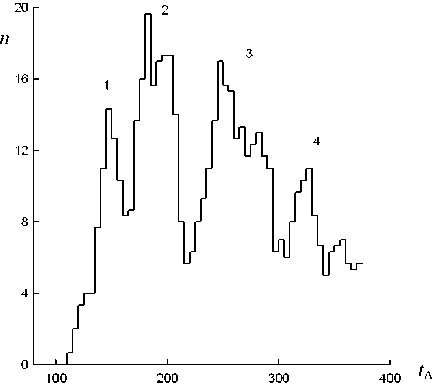
Рис . 2. Общее распределение значений t _A .

ностей определяется характерными временами пер вой и второй группы t A1 =130 с и t A2 =200 с . Однако из рис . 2 видно , что эти значения невозможно считать слишком точными , поскольку в пределах каждой группы наблюдается значительный разброс t _A. Осо бенно это касается второй группы . Кроме того , мы вынуждены пренебречь глубиной источников , хотя это и оправдано тем обстоятельством , что почти все обра ботанные землетрясения были мелкофокусными . Это значит , что в данной ситуации мы не можем добиться точного определения искомой глубины отражающих поверхностей . Мы можем получить только ее грубую оценку . С учетом того , что t A – это время пробега туда и обратно , получаем , что первая поверхность находится на глубине приблизительно 500 км , а вто рая – 800 км . Несмотря на грубость оценки , оказыва ется , что глубина , на которой расположена первая поверхность , неплохо согласуется с известной глу биной границы между слоями внутри астеносферы 420 км . Эта граница обнаружена еще на заре сейсмо логии [ Болт , 1984] и в настоящее время входит во все современные модели Земли . Согласно [ Буллен , 1966] на этой границе наблюдается скачек вертикального градиента скорости P- и S- волн , т . е . скорости волн начинают резко возрастать с увеличением глубины . Вторая обнаруженная нами поверхность оказалась на глубине , которая совпадает с глубиной 600–900 км , соответствующей местоположению границы между верхней и нижней мантией [ Буллен , 1966; Болт , 1984]. Таким образом , мы получили отражающие поверхности там , где они должны находиться на са мом деле . Это означает , что предлагаемый в данной работе метод обработки позволяет добиваться досто верных результатов .

Как уже было упомянуто выше, особенностью общего распределения tA является значительный разброс значений в пределах каждой отдельной группы. Уже в ходе обработки и формирования массива значений tA было установлено, что этот разброс не может быть обусловлен только погрешностью измерений. Оказалось, что он в значительной мере связан с разбросом географических координат эпицентров. Для источников, расположенных в разных точках земной поверхности, глубины, на которых находится отражающая поверхность, и скорости волн под источником могут существенно отличаться. Значит, отличаться должны и значения tA в пределах одной группы. Это приводит нас к необходимости построения распределений, аналогичных общему распределению, представленному на рис. 2, для каждого источника в отдельности. Однако в этом случае возникают определенные затруднения технического характера. Дело в том, что, как оказалось, записи не всех источников землетрясений позволяют сделать число измерений tA, достаточное для построения распределения. Указанное ранее процентное соотношение для случаев с отчетливыми пиками в КФАФ может существенно отличаться для разных записей. Для некоторых записей количество этих случаев оказывается просто недопустимо мало. Поэтому распределения tA мы строили только для тех источников, которые позволили набрать максимально возможное число измерений. Характеристики этих источников приведены в таблице. Распределения tA для каждого источника представлены на рис. 3. Номер, указанный на графиках, совпадает с номером источника в таблице.

Анализ распределений показывает , что все зна чения t _A, так же как на общем распределении , раз биваются на те же четыре отдельных группы . Пер вая и третья группы , как было показано , формиру ются временем пробега соответственно P- и S- волн вертикально вниз от источника до отражающей по верхности в астеносфере , на которой имеет место скачок вертикального градиента скорости волн . Вторая и четвертая группы определяются временем пробега волн до границы между верхней и нижней мантией . Очень любопытной особенностью этих распределений , которая совершенно незаметна на общем распределении , является то , что первая и третья группы имеют вид двух пиков с отчетливым минимумом между ними . Эта особенность очень чет ко наблюдается на всех без исключения распределе ниях , представленных на рис . 3, поэтому ее невоз можно считать случайным совпадением и отнести на счет не очень большого числа измерений времени t A в каждом распределении . Структура двойных пиков для первой и третьей групп ( на рис . 3 они обозначе ны 1a, 1b и 3a, 3b) может означать только то , что P- и S- волны отражаются не от одной , а от двух близко расположенных поверхностей . Времена пробега волн до этих поверхностей должны немного отли чаться друг от друга , что приводит к наличию двух характерных значений t A в каждой из указанных групп . Полученный результат ясно свидетельствует о том , что в астеносфере на глубине скачка градиен та скорости должен располагаться тонкий слой ве щества , по своим свойствам отличающийся от ок ружающей среды . При этом волны могут отражаться как от верхней , так и от нижней поверхности слоя .

Вторая особенность рис . 3 связана с распределе ниями 3 и 4. На этих распределениях отчетливо видны одинаковые последовательности пиков , наблюдаю щиеся на всех без исключения представленных рас пределениях . Пики 1a и 1b соответствуют временам t A1a и t A1b прохождения ( туда и обратно ) P- волны вер тикально вниз от источника до соответственно верх ней и нижней поверхности слоя . Пик 2 соответствует

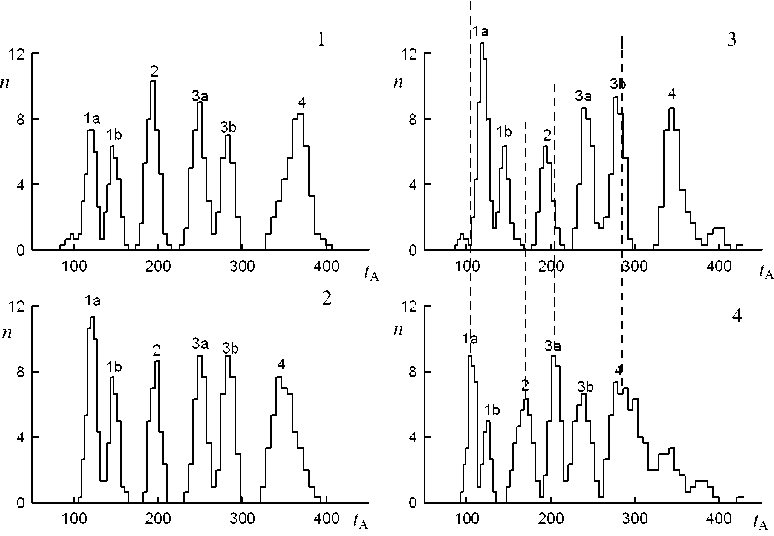
Рис . 3. Распределения измерений времени t _A для четырех разных источников .

№	Дата	Время начала (UT)	Широта	Долгота	Регион	Глубина	Магнитуда
1	2000.05.04	04:21:16	–1.1º	123.6º	Сулавеси	26 км	7.6
2	2000.06.18	14:44:13	–13.8º	97.5º	Индийский океан	10 км	7.8
3	2000.02.25	01:43:58	–19.5º	173.8º	о - ва Вануату	33 км	7.1
4	1999.02.06	21:47:59	–12.8º	166.7º	о - ва Санта - Круз	90 км	7.4

времени пробега tA2 P-волны от источника до границы между верхней и нижней мантией. Пики 3a, 3b и 4 определяются временами tA3a, tA3b и tA4 пробега S-волны до тех же самых поверхностей. На рис. 3 отчетливо видно, что пики на распределениях 3 и 4 сдвинуты по tA относительно друг друга таким образом, что время всех пиков 4 оказывается меньше времени соответствующих пиков 3. При этом сдвиги пиков для S-волн существенно превышают по величине сдвиги пиков для P-волн. Согласно таблице, эпицентры источников 3 и 4 располагаются недалеко друг от друга на угловом расстоянии 10º в районе островов Санта-Круз и Вануату в Тихом океане. Поэтому мы можем считать, что для обоих этих источников отражающие поверхности находятся на одной и той же глубине. Значит, источник 4, глубина которого 90 км, располагается к этим поверхностям ближе, чем источник 3, глубина которого 33 км. Следовательно, время пробега волн от источника 4 должно быть меньше, чем время пробега от источника 3 до тех же самых поверхностей. Причем, поскольку скорость S-волн меньше скорости P-волн, то разница во времени пробега для S-волн от обоих источников должна быть больше, чем для P-волн. Тот факт, что время пиков в распределениях 3 и 4 на рис. 3 оказывается зависимым от глубины источника, подтверждает выводы предыдущего раздела данной работы и, значит, косвенно свидетельствует о достоверности получаемых результатов по измерениям tA. Кроме того, это дает уникальную возможность для экспериментального определения скорости P- и S-волн. Действительно, получается, что смещение пиков 1a, 1b и 2 должно быть одинаковым и определяться удвоенным временем движения в вертикальном направлении P-волны от одного источника до другого. Смещение пиков 3a, 3b и 4 определяется аналогичным временем для S-волны. При этом путь, проходимый волнами, есть разность глубины источников и в данном случае составляет 57 км. Измеряя временное смещение каждого пика, находим по три значения скорости VP и VS. Вычисляя среднее значение и статистическую погрешность, получаем VP=(6.4±1.2) км/с, VS=(3.0±0.2) км/с. Эти значения определяют средние скорости волн на глубине от 33 км до 90 км в локальной области, координаты которой соответствуют координатам источников 3 и 4 из таблицы. Если сравнить полученные скорости с известными из сейсмологии [Буллен, 1966; Болт, 1984] значениями скорости на той же глубине, то обнаруживается очень неплохое совпадение.

Необходимо также отметить универсальный характер предлагаемого способа измерения скоростей VP и VS. С его помощью скорости можно определять на любой заданной глубине в пределах верхней мантии для разных регионов на земной поверхности. Для этого на упомянутом выше сайте достаточно выбрать записи смещения на одной из сейсмических станций мировой сети от двух источников землетрясения. Эпицентры источников должны находиться в заданном регионе, а по вертикали они должны быть немного разнесены и попадать в окрестность заданной глубины. По указанной выше схеме записи смещения обрабатываются вплоть до построения распределения tA для каждого источника. После это- го на каждом распределении выявляются аналогич- ные пики и определяется их временное смещение. Это смещение определяется временем пробега волн между источниками, а расстояние между ними находим с помощью того же сайта, где всегда указывается глубина источника. Искомые скорости определяются как отношение известного расстояния и измеренного времени пробега волнами этого расстояния.

Вернемся снова к решению вопроса, на какой глубине располагаются выявленные нами отражающие поверхности. На сей раз определить эту глубину мы можем значительно точнее, с учетом глубины источника, и, самое главное, не прибегая к использованию значений скорости волн, принятых в сейсмологии. Измеренные значения скорости VP и VS относятся к району островов Санта-Круз в Тихом океане. Будем считать, что эти скорости не очень сильно меняются с глубиной в пределах верхней мантии. Для того чтобы определить глубину верхней отражающей поверхности упомянутого выше слоя в этом районе, мы должны для распределений 3 и 4 tA1a или tA3a умножить с коэффициентом 0.5 на соответственно VP или VS и прибавить глубину источника из таблицы. Определяя среднее значение и погрешность этих измерений, получаем, что верхняя поверхность слоя находится на глубине (409±8) км, которая согласно [Буллен, 1966; Болт, 1984] почти идеально совпадает с глубиной скачка вертикального градиента скорости P- и S-волн 410 км. По-видимому, этот скачок как раз и обусловлен наличием слоя. Толщину слоя можно определить по разности времен tA1b и tA1a в каждом из распределений 3, 4 для скорости VP, а также по разности tA3b и tA3a для скорости VS. Получается, что слой имеет толщину (64±5) км. Глубину еще одной обнаруженной нами отражающей поверхности находим аналогично по временам tA2 и tA4 для измеренных скоростей VP и VS. Получаем с учетом погрешности (590±30) км, что довольно неплохо соответствует глубине границы между верхней и нижней мантией 640 км [Болт, 1984]. Таким образом, глубина слоя и второй отражающей поверхности в еще большей степени приблизилась к известным границам раздела земных оболочек. Этот факт должен служить еще одним подтверждением достоверности получаемых результатов.

Распределения, представленные на рис. 3, дают возможность определения отношения скорости P- и S-волн на различных глубинах в верхней мантии. Это отношение, согласно (4), (6) в первой части данного исследования, имеет вид

V P

V S

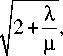
где λ и µ – параметры Ламе, характеризующие упругие свойства вещества. Отношение λ/µ можно рассматривать как одну из характеристик агрегатного состояния вещества, в котором распространяются упругие волны. Действительно, для жидкости модуль сдвига µ очень мал, что соответствует условию λ/µ>>1. Для твердого кристаллического вещества имеет место противоположное неравенство λ/µ<<1. Значит, чем больше отношение λ/µ, тем более жидким должно быть вещество. Для распределений, представленных на рис. 3, времена пиков tA1a и tA3a являются временами пробега P- и S-волнами одинакового расстояния от источника до верхней границы обнаруженного нами слоя. Значит, отношение tA3a/tA1a должно совпадать с отношением средних значений скоростей VP и VS на пути пробега. С учетом (2) для каждого распределения можно вычислить отношение λ/µ. После этого находим среднее значение и статистическую погрешность для вещества в области от земной поверхности до верхней границы слоя: λ/µ=2.1±0.2. Интересно отметить, что полученные ранее значения скоростей VP и VS на глубине от 33 км до 90 км дают примерно такое же отношение λ/µ =2.4. Одинаковое расстояние, равное толщине слоя, P- и S-волны проходят соответственно за времена tA1b–tA1a и tA3b–tA3a. Отношение этих разностей должно совпадать с отношением VS и VP в слое. С учетом (11), аналогично получаем для вещества в слое λ/µ=0.2±0.3. Время пробега P- и S-волн от нижней кромки слоя до границы между верхней и нижней мантией составляет tA2–tA1b и tA4–tA3b. Точно так же, как в предыдущих случаях, используя соотношение (11), получаем для вещества между слоем и нижней границей верхней мантии λ/µ=0.2±0.2. Последние два значения λ/µ имеют большую относительную погрешность, поэтому их нельзя считать слишком достоверными. Однако даже в данном случае эти значения оказываются, как минимум, в 5 раз меньше значений λ/µ выше слоя. Следовательно, вещество в слое и ниже его, вплоть до нижней границы верхней мантии, должно быть гораздо более твердым, чем вещество в области над слоем.

Необходимо обратить внимание на локальность полученных нами результатов . По определению вре мя пиков распределений , представленных на рис . 3, есть время пробега упругих волн вертикально вниз под источником . Большинство источников , согласно координатам эпицентров из таблицы , сосредоточено в западной части Тихого океана . Значит , вывод о соотношении параметра λ / µ на разной глубине дол жен относиться только к этому региону земной по верхности . Для других регионов этот вывод может оказаться неприменимым . То же самое относится к обнаруженному на глубине 400 км слою . Мы можем только утверждать , что этот слой имеет место под указанным регионом . Значит , более корректно будет считать , что это не слой , а плита , имеющая , возмож но , ограниченные горизонтальные размеры .

Сформулируем основные результаты данного раздела :

• 1.    Для региона западной части Тихого океана на глубине 410 км обнаружен слой вещества ( или пли та ) толщиной примерно 70 км . Вещество в слое и ниже его , вплоть до нижней границы верхней ман тии , оказывается ( по величине отношения λ / µ ) зна чительно более твердым , чем вещество в области выше слоя . Глубина верхней поверхности слоя сов падает с известной [ Буллен , 1966] глубиной скачка вертикального градиента скорости P- и S- волн .

• 2.    Показано , что предлагаемый в данной рабо те метод позволяет определять время пробега P- и S- волнами известного расстояния между очагами двух землетрясений на различной глубине верхней мантии . Это дает возможность для прямого опреде ления средней скорости волн как отношения рас стояния и времени . Измеренные таким способом скорости волн в районе островов Санта - Круз в Ти хом океане на глубине от 33 до 90 км имеют значе ния V P =(6.4±1.2) км / с и V S =(3.0±0.2) км / с .

В заключение данного раздела следует обратить внимание на наиболее важную, пожалуй, для практического использования особенность предлагаемого метода. Пики 1a и 3a на распределениях рис. 3, соответствующие минимальной глубине отражающей поверхности, образуются при обработке самой высокочастотной составляющей записей смещения земной поверхности. Максимально возможная частота выделяемых путем фильтрации монохроматических колебаний определяется шагом оцифровки исходных записей. Тот факт, что минимальная глу- бина обнаруженных нами отражающих поверхностей оказалась равной 400 км, обусловлен только тем, что шаг оцифровки наших исходных данных составляет 1 с. Если использовать данные с меньшим шагом, то можно выявлять отражающие поверхности на меньшей глубине. Например, если шаг оцифровки будет 0.1 с, то отражающие поверхности могут быть обнаружены, начиная с глубины примерно 40 км. При еще меньшем шаге мы, вероятно, получим возможность для зондирования слоев на глубинах земной коры. Значит, предлагаемый нами метод может оказаться эффективным для поиска полезных ископаемых.