Новый подход к интерпретации волновой функции одночастичного уравнения Клейна - Фока - Гордона

Известно, что последовательная релятивистская квантовая механика не может быть развита как теория одной частицы (см., например, [1]). Из-за рождений и аннигиляций частиц, такая теория может быть только многочастичной. Однако есть большой круг проблем, где одночастичное приближение дает хорошие результаты.

Например, уравнение Дирака с большой точностью правильно описывает спектр излучения атома водорода и другие явления.

Применение же уравнения КФГ к одночастичным явлениям считается неприемлемым в связи с трудностью вероятностной интерпретации волновой функции этого уравнения. В учебной литературе по этим вопросам утверждается, что уравнение КФГ не позволяет ввести положительно определенную величину, которую можно было бы истолковать как плотность вероятности, аналогичную плотности вероятности нерелятивистского уравнения Шредингера (см., например, [2]).

Хорошо известно, что если Ф волновая функция некоторой системы, то уравнение Шредингера позволяет ввести сохраняющуюся величину Ф*Ф, которая интерпретируется как плотность вероятности. В случае же уравнения КФГ соответствующая величина имеет вид

ф*-- 9t

^^^^^^^™

т ЭФ

Ф----.

dt

Это выражение сохраняется, но положительно не определено и нельзя интерпретировать как плотность вероятности. Но возникает вопрос. Почему такое сложное выражение нужно истолковывать как плотность вероятности? Может быть это выражение есть некоторая сохраняющаяся физическая величина, если Ф имеет тот же смысл, что и в уравнении Шредингера?

В данной работе будет дано обоснование, что волновая функция уравнения КФГ может быть интерпретирована, как и в уравнении Шредингера, в борновском смысле. Будет показано, что уравнение КФГ дает закон сохранения энергии, а не числа частиц

(закон сохранения плотности вероятности выражает, в конечном счете, сохранение числа частиц) [3].

Сначала мы рассмотрим уравнение КФГ для свободной частицы, а потом для заряда в электромагнитном поле. Причем метод введения электромагнитного поля может быть применен и в классической физике для уравнения Гамильтона — Якоби.

Тем самым будет показано, что введение калибровочного поля в квантовой механике, связанное с локальной фазовой инвариантностью, можно было проводить и в классической физике.

• 2.    Уравнение КФГ для свободной частицы и интерпретация фазы волновой функции

Как хорошо известно, уравнение КФГ можно записать в форме [1-2]

52Ф           9

—— = У²Ф - _т²ф. at²

Обозначения стандартные и h = с = 1.

Записав (1) для комплексно-сопряженной функции Ф* обычным способом можно получить

8 (^9^ — Ф* — 8t V 8t

^^^^^^^™

т ЭФ

Ф--

8t

)

= V (Ф*УФ - ФУФ*).

Закон сохранения какой физической величины выражает уравнение (2)? Обычно это уравнение связывается с уравнением непрерывности для плотности вероятности, а плотность вероятности считается ~ Ф*^" — ^дуд- Здесь и возникает трудность со знаком. Но, поскольку плотность вероятности связана с числом частиц, а число частиц в релятивистской области не обязано сохраняться, то можно предположить, что уравнение (2) выражает закон сохранения некой другой физической величины.

Для исследования этого вопроса, следуя работам [3, 5-7], представим Ф в виде

Ф = рз exp('iS),

где р = ф*ф и S — вещественные получаем

произвольные функции. Подставляя (3) в (2) легко

Анализ уравнения (1) с помощью подстановки (3) проведен в работе [3]. Здесь мы пойдем несколько иным путем. Умножив (1) слева на Ф*, и интегрируя по пространственным координатам, получим:

/ ^*^^^{dV =} / Ф^²Ф(/К — т² j Ф*Фс/К

где dV = dxdydz.

Подставляя (3) в (5), после несложных преобразований, получим

lV»--^V-ДЖ) -’Ж-

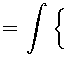
P^V Р2

-p^Sf^dV

^^^^^^^™

m

j pdV.

Учитывая (4) и приравняв подынтегральные выражения, из (6) получаем

1 /dS\ ²      2   2 2 _ ^ (⁹V² _V2 Л

Здесь и далее будем пользоваться обычными единицами.

Отметим, что, если бы (4) мы не получили из (2), то получили бы из (6), так как нужно приравнять действительные и мнимые части (6).

Уравнения (4) и (7) получены из (1) подстановкой (3) чисто формальным образом и до сих пор мы никак не интерпретировали р и S. Если в (7) постоянную Планка К —> 0, то получаем релятивистское уравнение Гамильтона — Якоби для классического действия S [4].

Найдем нерелятивистский предел (4) и (7). Для этого представим S в виде S = Sq — mc²t. Подставляя это выражение в (4) и (7), получим

| + v№ V at у m у

1 9

me2 9t

/ 98 A

V dt У

9t 2m ° 2m p^ 2mc²

ZdSgV h² 9² p^

\ 9t у 2mc2p^ dt2 ' ,

Из (8) видно, что в пределе при с —> оо эти уравнения переходят в соответствующие уравнения, получаемые из уравнения Шредингера для свободной частицы при подстановке (3) [5-7].

В [5-7] величина —h²V²p?[2mp^ названа «квантовым потенциалом» или «квантово-механической энергией».

В работах [5-7] положительно определенная величина р имеет обычный смысл плотности вероятности. Следовательно, и в случае уравнения КФГ (1) мы можем определить р как плотность вероятности и проводить по этой функции усреднения разных величин. Чтобы выяснить физический смысл фазы S поступим следующим образом.

Найдем среднее значение оператора импульса Р = —ih,V. Имеем

(F) = -гП I

^*V^dV.

Подставляя (3) в (9), с учетом того, что на бесконечности р —> 0, легко получим

(Г) = / p^SdV.

Выражение (10) позволяет нам интерпретировать величину Р(г, 1) = VS как импульс частицы в данной точке в момент t. Точка г распределена с вероятностью р^т, t), что соответствует соотношению неопределенности. Тем самым устанавливается смысл VS.

Чтобы установить смысл dS/ dt, запишем уравнение Шредингера в форме справедливой как в нерелятивистской, так и в релятивистской квантовой теории, т. е. в виде

ЭФ

(П)

гП— = ЯФ. dt

Умножая (11) слева на Ф* и интегрируя, получим

Г ШФ Г гП / Ф ~dtdV = H^dV'

Физический смысл правой части (12) ясен, это (Я). Подставляя (3) в левую часть (12), с учетом нормировки р, получим

-jp^-I^H»^ т.е. ^)--Ф>.

Таким образом мы можем утверждать, что dS/dt есть локальная энергия частицы с обратным знаком. Если же S представимо в виде S(r, t) = So (г) — Et, где E = const, то получим

Эр

-2. + div; = 0, at

где ;' = ^j (Ф*\7Ф — ФХ^Ф*) в случае уравнения (2) и ; = ^pXSo в случае уравнения (4). При Я < 0 уравнение (14) имеет вполне разумное истолкование [3].

Вернемся теперь к (4). Интегрируя (4) по объему и применяя к правой части теорему Остроградского — Гаусса, получим а г as . г

-у / P^rdV = c2 pVSda, at j at j

где dcr — вектор элемента поверхности a.

Пусть p достаточно быстро стремится к нулю при г —> ос. Тогда при ст —> оо, получим

С учетом (13) мы получили закон сохранения энергии в интегральной форме. Следовательно, мы можем интерпретировать (4) как закон сохранения в дифференциальной форме.

Из этих рассуждений можно сделать вывод: уравнение КФГ дает закон сохранения энергии, а не плотности вероятности (плотности числа частиц) и знак р никак не связан с уравнением непрерывности (2).

• 3.    Локальная инвариантность и учет взаимодействия

Если частица с зарядом q движется в электромагнитном поле с потенциалами А и р, то записав уравнение КФГ для этого случая и сделав подстановку (3), мы получим соответствующее обобщение (4) и (7). В работе [3] получены эти уравнения указанным способом.

Здесь мы включим взаимодействие несколько иным способом. Как видно из (4) и (7) эти уравнения инвариантны относительно замены S —» S' + const. Если же сделать замену S —> S' + const • /(ж,!), где / — произвольная функция, то уравнения уже не инвариантны. Теперь потребуем, чтобы при такой замене S уравнения (4) и (7) оставались бы инвариантными, т. е. потребуем локальную инвариантность уравнений (4) и (7) при преобразованиях S —> S' + const • /(ж, t). Тогда мы должны ввести некоторые «поля», которые бы компенсировали лишние члены.

Подвергнем S преобразованию

S S' + - -f^HY с

Тогда

Э8__ Э8_ q_8j_ dt dt с dt

И VS = VS'+-V/. с

Чтобы исчезли лишние производные в (4) и (7), как видно из (18), нужно ввести компенсирующие поля. Введем поля в (4) и (7) в виде

^{^ + ^} = =2v{,(vS-^)};

(^+Ч -г Л - Л -т2с2=^ (^ -^р1) ■

Теперь одновременно с (17) преобразуем поля по формулам

V = У⁵' -

1д/ с dt ’

А = А' + V/.

Видно, что уравнения (19) не меняют своей формы. А (20) есть хорошо известные калибровочные преобразования электромагнитных потенциалов. Эти рассуждения интересны еще и тем, что, как уже отмечалось выше, при К —> 0 уравнение (7) переходит в классическое уравнение Гамильтона — Якоби. Следовательно, преобразования (17) и (20) имеют место уже в классической физике, если потребовать локальную инвариантность классического действия. То есть электромагнитное поле можно было бы в принципе «предсказать» теоретически после формулировки уравнения Гамильтона — Якоби.

Теперь покажем, что относительно преобразования типа (17), уравнение движения классической механики инвариантно.

По определению имеем dS_c/dt = L, где S_c — действие, L — функция Лагранжа. Если одновременно провести преобразования

S_c = S' + af;

L = L' A adf /dt;

где a = const и / — произвольная функция, то dS'Jdt = L' . Как известно, функция Лагранжа определена с точностью до полной производной от произвольной функции, так как уравнение движения определяется условием 5S_C = 0.

Любопытно отметить, что на этот факт не обращают внимания в учебной литературе.

• 4.    Заключение

Как известно [5, 6], Фейнман развил гидродинамический подход к проблеме сверхпроводимости, основанный на уравнении Шредингера. Поскольку сверхпроводящие куперовские пары — скалярные частицы, то к ним можно применить уравнение КФГ при вероятностном истолковании волновой функции. Тем самым уравнения (19) обобщают подход Фейнмана на релятивистскую область.