О бифуркациях некоторых сепаратрисных контуров кусочно-гладкой динамической системы с симметрией

В настоящей заметке описаны бифуркации в типичном однопараметрическом семействе кусочно-гладких векторных полей на плоскости, инвариантных при отражении относительно прямой, в которых рождается пара симметричных устойчивых предельных циклов .

Пусть D – разбиение R ² на множества D_k , k ∈ {1, 2,..., n } с C ^∞ -гладкими границами ∂ D_k , такие, что их пересечения D_i ∩ D_j , i ≠ j , совпадают с ∂ D_i ∩ ∂ D_j , а X ^k – векторные поля класса C^r на D_k . Кусочно-гладким векторным полем на плоскости R ² , задаваемым полями X^k , называется класс всех векторных полей X ^ɶ на R ² таких, что в точках z ∈ int D_k X ^ɶ ( z ) = X ^k ( z ) . Будем его обозначать X = ( X ¹, X ²,..., X ⁿ ) . Траектории векторных полей X ^ɶ будем задавать, используя выпуклое доопределение в точках линий переключения ∂ D_i ∩ ∂ D_j [1]. Они не зависят от выбора представителя класса и потому их можно называть траекториями поля X .

Пусть отображение I : R ² → R ² , I ( x , y ) : = ( x , - y ) сохраняет разбиение D , то есть ∀ k ∈ {1,2,..., n } ∃ l ∈ {1,2,..., n } I ( D_k ) = D_l , а границы множеств D_k не касаются множества неподвижных точек инволюции I – оси x . Кусочно-гладкое векторное поле X = ( X ¹, X ²,..., X ⁿ ) назовем инвариантным относительно I , если ∀ k ∈ {1, 2,..., n } ∀ z ∈ D_k IX ^k ( z ) = X ^l I ( z ), где D_l = I ( D_k ) . Множество таких полей обозначим Vec ^r ( D , I ) .

Предположим, что O = (0, 0) ∈ D ⁰ : = D_L ∩ D_R при некоторых L , R ∈ {1, 2,..., n } . Тогда I ( D_L ) = D_L , I ( D_R ) = D_R , I ( D ⁰) = D ⁰ и в достаточно малой окрестности точки O G ⁰ задается

Ройтенберг В.Ш.

уравнением z ₁ = g ( z ₂) , где g – четная C ^∞ -гладкая функция. Перейдем к этой окрестности к координатам x = z ₁ - g ( z ₂) , y = z ₂ . Инволюция I переводит точку с координатами ( x , y ) в точку с координатами ( x , - y ) . В окрестности V _δ ( O ) точки O , задаваемой в координатах ( x , y ) неравенствами x <  δ , | y | <  δ , где δ – достаточно малое положительное число, D ⁰ имеет уравнение x = 0 и можно считать, что V _δ ( O ) ∩ D_L ( V _δ ( O ) ∩ D_R ) дается неравенством x ≤ 0 ( x ≥ 0 ). Далее будем отождествлять точку из V _δ ( O ) с ее координатной строкой ( x , y ) .

• 2.    Условия и результаты. Пусть разбиение D такое, как описано выше. Рассмотрим однопараметрическое семейство векторных полей X _µ = ( X _µ ¹ ,..., X _µ ⁿ ) ∈ Vec ^r ( D , I ) , µ ∈ ( - µ ₀, µ ₀) , такое, что векторы X _µ ^k ( z ) , k ∈ {1, 2,..., m } , C^r -гладко зависят от ( z , µ ) ∈ G_k × ( - µ ₀, µ ₀) , r ≥ 3 .

Векторное поле X _µ ^L _{V δ ( O ) ∩ DL} можно продолжить до C^r -векторного поля X _µ ^L на V _δ ( O ) , инвариантного относительно I так, что вектор X _µ ^L ( z ) C^r -гладко зависит от ( z , µ ) ∈ V _δ ( O ) × ( - µ ₀, µ ₀) [13, с. 587]. Пусть в координатах ( x , y )

X _µ ^L ( z ) = P ( x , y , µ ) ∂ / ∂ x + Q ( x , y , µ ) ∂ / ∂ y .

Вследствие инвариантности поля X _µ ^L

P ( x , - y , µ ) ≡ P ( x , y , µ ), Q ( x , - y , µ ) ≡- Q ( x , y , µ ) .                       (1)

Пусть O – особая точка поля X ₀ ^L , то есть

P (0,0,0) = Q (0,0,0) = 0 .                                    (2)

Ввиду (1) P_y ′ (0, 0, 0) = Q_x ′ (0, 0, 0) = 0 и потому λ ₁ ⁰ : = P_x ′ (0, 0, 0) и λ ₂ ⁰ : = Q_y ′ (0, 0, 0) – собственные значения матрицы линейной части в точке O . Они не зависят от произвола в выборе векторных полей X _µ ^L . Предположим, что λ _k ⁰ <  0 ( k = 1,2) , то есть точка O – грубый устойчивый узел поля X ₀ ^L , Знак P _µ ′ (0, 0, 0) зависит только от векторных полей X _µ ^L . Потребуем, чтобы P _µ ′ (0, 0, 0) ≠ 0 . Без ограничения общности можно считать

P µ ′ (0,0,0) > 0,                                           (3)

поскольку случай P _µ ′ (0, 0, 0) <  0 сводится к случаю P _µ ′ (0, 0, 0) >  0 заменой µ на - µ .

Пусть точка S ₀ = ( x ₁ ⁰ ,0) ∈ int G_kS ( k_S ∈ {1, 2,..., m } ) является грубым седлом векторного поля X ₀ ^{k S} с характеристическими показателями λ ₁ ^S ₀ >  0 и λ ₂ ^S ₀ <  0, открытая дуга L ⁱ ₀ ⁿ оси x между точками O и S ₀ не содержит особых точек поля X ₀ и является входящей сепаратрисой седла S ₀ , а выходящие сепаратрисы L ⁺ ₀ и L ^- ₀ = I ( L ⁺ ₀ ) точки S ₀ , лежащие, соответственно, в верхней и нижней полуплоскостях, не содержат особых точек поля X ₀ и ω -предельны к O (рис. 1).

Сепаратрисные контуры Γ0± := Li0n ∪ L±0 ∪ {O, S0} симметричны: I(Γ0±) = Γ0∓ , и образуют по- лицикл Γ0 := Γ0+ ∪ Γ0- .

Будем рассматривать два варианта:

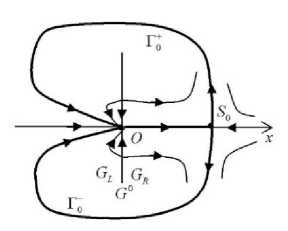
Рис. 1. Полицикл Γ ₀ : = Γ ₀ ⁺ ∪ Γ ₀ ^-

• (А) Выполняется условие P_y ′ _y ′ (0, 0, 0) <  0 .

(Б) Ось x – ведущее направление узла O , то есть λ ₂ ⁰ <  λ ₁ ⁰ . Сепаратрисы L ⁺ ₀ и L ^- ₀ входят в O по ведущему направлению . Седловой индекс / ₀ : = -A S / A S Ф 1.

Теорема. В случаях (А) и (Б) найдутся число µ ∈ (0, µ ₀ ] и окрестность U полицикла Γ ₀ , I ( U ) = U , со следующими свойствами:

Математика

• 1)    Для любого µ ∈ (0, µ ) векторное поле X _µ имеет в U две орбитно устойчивые периодические траектории: Γ _µ ⁺ , лежащую в верхней полуплоскости, и Γ _µ ^- = I ( Γ _µ ⁺ ) , лежащую в нижней полуплоскости, а их топологические пределы lt Γ _µ ^± = Γ ₀ ^± . В случае (Б) Γ _µ ⁺ и Γ _µ ^- являются µ → 0 + ^{µ                     µ µ}

гиперболическими периодическим траекториями, а в U нет других периодических траекторий.

• 2)    При µ ∈ ( - µ , 0] у векторного поля X _µ в U нет периодических траекторий .

• 3.    Случай (А) . По теореме о неявной функции из (1)–(3) следует, что при некотором µ ₁ >  0 для всех µ ∈ ( - µ ₁ , µ ₁ ) векторное поле X _µ ^L имеет грубый устойчивый узел O _µ с координатами x = ξ ( µ ) , y = 0, где

Доказательство теоремы приведено в разделах 3–4.

ξ ( ⋅ ) ∈ C ^r , sgn ξ ( µ ) = sgn µ ,                                   (4)

с матрицей линейной части поля в точке O _µ равной diag( λ ₁( µ ), λ ₂( µ )) , где λ ₁ ( µ ) : = P_x ′ ( ξ ( µ ),0, µ ) и λ 2 ( µ ): = Q y ′ ( ξ ( µ ),0, µ ).

Ввиду (1) Q ( x ,0, µ ) = 0, и потому Q ( x , y , µ ) = y ( λ ₂ ( µ ) + r ₁ ( x - ξ ( µ ), y , µ )), где r ₁ ∈ C ¹ , r ₁(0, 0, µ ) = 0 . Следовательно, числа d ∈ (0, δ ], µ ₂ ∈ (0, µ ₁] можно выбрать так, что

Q(x, y,µ) ≤(λ20 /2)y при I x I ≤ d , 0 < y ≤ d , µ∈ (-µ2,µ2) .(5)

Линейная часть функции P ( x , y , 0) равна λ ₁ ⁰ x . Поэтому можно считать, что P ( - d , y , 0) >  0 при всех y ∈ [ - d , d ] . Фиксировав d , мы можем выбрать µ ₃ ∈ (0, µ ₂] так, что

P(-d,y,µ) > 0 при всех y ∈ [-d,d] , µ∈ (-µ3,µ3) .(6)

Вследствие (1) P (0, ⋅ , µ ) – четная функция, и потому

P(0,y,µ)=P(0,0,µ)+y2[Py′′y(0,0,0)+R(y,µ)],(7)

где R ∈ C1 , R(0, 0) = 0 . Отсюда, из (2) и (3) следует, что уравнение P(0, y, µ) = 0 имеет решения только при µ ≥ 0 . При y ≥ 0 оно равносильно уравнению y V-Py′′y(0,0,0)+R(y,µ)=VP(0,0,µ) . Перепишем его в виде y 7 -Py′′y(0,0,0)-νVP(0,0,0)+R1(y,ν)=0,(8)

где ν = µ , а R1 (y,ν) – C1 -функция, определенная в некоторой окрестности точки (0, 0) , R1(0, 0) = (R1)′y(0,0) = (R1)ν′ (0, 0) = 0 . По теореме о неявной функции найдутся такое число µ4 ∈ (0, µ3] , что для любого ν ∈ (- µ4 , µ4 ) уравнение (8) имеет решение y=yˆ(ν)=ν7-Pµ′(0,0,0)/Py′′y(0,0,0)+o(ν).

Выбрав µ ₄ достаточно малым, получим

0 <   y ˆ( µ ) ≤ K µ <  d / 2 при µ ∈ (0, µ ₄) ,                        (9)

где K = 2 7 -Pµ′ (0, 0, 0) / Py′′y(0, 0, 0) . Следовательно, при µ∈ [0,µ4) yˆ( µ) – решение уравнения P(0, y,µ) = 0 . Ввиду (2) и (7) можно считать Py′(0, y,µ) < 0 при y ∈ (0,d] , µ∈ [0, µ4) . Поэтому sgn P(0, y,µ) = sgn( yˆ( µ)-y) при всех y∈(0,d], µ∈[0,µ4).                 (10)

Пусть d / 2 <  d ₁ <  d . Обозначим множество точек из V _δ ( O ) ∩ G_L с координатами ( x , y ) ∈ [ - d , 0] × (0, d ₁] символом Π , с координатами ( x , y ) ∈ ( - d , 0) × { d ₁} символом l ₁ и с координатами ( x , y ) ∈ { - d } × (0, d ₁) символом l ₂ . Ввиду (5) и (6) d ₁ можно считать выбранным так, что траектория L ⁺ ₀ пересекает границу Π в единственной точке, принадлежащей одной из дуг l ₁ или l ₂ , трансверсально этой дуге. Для определенности, пусть эта точка принадлежит l ₁ и име ет координаты x = u ₀ , y = d ₁ . Случай, когда точка принадлежит l ₂ , рассматривается аналогично.

Ройтенберг В.Ш.                        О бифуркациях некоторых сепаратрисных контуров кусочно-гладкой динамической системы с симметрией

При достаточно малом µ ₄ поле X _µ ^kS , µ ∈ ( - µ ₄, µ ₄) , имеет грубое седло S ( µ ) с координатами x ₂ = 0 , x ₁ = x ˆ₁( µ ) , x ˆ ₁ ( ⋅ ) ∈ C ^r , x ˆ₁(0) = x ₀ и характеристическими показателями λ ₁ ^S ( µ ) >  0

и λ ₂ ^S ( µ ) <  0 , C^{r - 1} -гладко зависящими от µ .

Пусть Gε0– дуга G0 , задаваемая в координатах (x, y) неравенством 0 < y ≤ ε . Поскольку сепаратриса L+0 не содержит особых точек, то из [14, п. 13.8] следует, что при достаточно малых ε и µ4 траектория поля Xµ , µ∈ (-µ4,µ4) , начинающаяся в точке Gε0 с координатой y = v ∈ (0,ε] , пересекает дугу l1 в точке с координатой x =ψ(v, µ) , где x = i/( v, p) = й( p) + c (p) vr(p) + p (v, p),                            (11)

S

й( - ), c ( • ) € C 1 , u (0) = u 0 , / ( p ) = - ^ 2^ ) >  0, | p ( v , p ) | <  v ^{r ( p ) + a} , p v ( v , p )| <  v ^{( p ) + a - 1} , 0 <  a <  1 . (12) λ ₁ ^S ( µ )

Доопределим ψ ( v , µ ) при v = 0 , положив ψ (0, µ ) : = u ˆ( µ ) . Из (11) и (12) получаем, что ε и µ ∈ (0, µ ₄] можно выбрать столь малыми, что

ψ ( v , µ ) ∈ ( - d , 0) для всех v ∈ [0, ε ] , µ ∈ ( - µ , µ ) .                     (13)

Из (5), (6), (10), (9) и свойств функции соответствия по траекториям между дугами без контакта [15, c. 81] следует, что положительная полутраектория поля X _µ ^L , µ ∈ (0, µ ₄) , начинающаяся в точке дуги l ₁ с координатами x = u ∈ ( - d , 0) , y = d ₁ трансверсально пересекает дугу x = 0 в точке с координатой y = ϕ ( u , µ ) , где ϕ ∈ C^r , ϕ _u ′ ( u , µ ) >  0 , 0 < ϕ ( u , µ ) < η ˆ( µ ) ≤ K µ .

Выберем 0 <  µ <  ε ² / K ² . Тогда

0 <  ϕ ( u , µ ) <  ε при всех u ∈ ( - d , 0) , µ ∈ (0, µ ) .                    (14)

Из (13) и (14) получаем, что при µ∈ (0,µ) определена функция f (⋅,µ) :=ϕ(ψ(⋅,µ),µ) , отображающая [0,ε] в (0,ε) . Она имеет хотя бы одну устойчивую неподвижную точку v0(µ)∈(0,K µ)⊂ (0,ε).                                    (15)

Поскольку f ( v , µ ) при v ∈ (0, ε ) является функцией последования по траекториям поля X _µ на

Gε0 , то через точку Gε0 с координатой y = v0 (µ) проходит единственная траектория Γµ+ , причем она орбитно устойчива. Поскольку число ε можно выбрать произвольно, то из (14) следует, что lt µ→0+

++

Γ _µ = Γ ₀ .

При µ∈ (-µ, 0] из (4) вытекает, что поле Xµ имеет в Π особую точку Oµ, к которой ω- предельны все траектории, начинающиеся в Π .

Построим простые замкнутые кривые r p , r p и / p ^xt, p € ( - p , p ), следующим образом. Кривая r p состоит из дуги траектории поля X _µ между точками A ₁ ⁺ ∈ G _ε ⁰ с координатой η = ε и точкой A ₂ ⁺ ∈ l ₁ , а также дуги ∂Π между этими точками (рис. 2). Кривая r p = I( r p ). Мы можем выбрать точки Bp в верхней полуплоскости и точку B ₁⁰ на оси x так, чтобы отрезок [ B ₁ ⁰ B ₁ ⁺ ] был трансверсален траекториям векторных полей X _µ ^S при всех

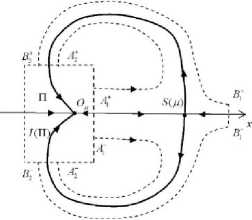
Рис. 2. Окрестность U _µ

µ ∈ ( - µ , µ ) , а положительные полутраектории поля X _µ , начинающиеся в точках [ B ₁ ⁰ B ₁ ⁺ ]\ B ₁⁰ , пересекали трансверсально дугу l ₁ . Пусть B ₁ ⁺ B ₂ ⁺ – дуга полутраектории траектории, начинаю-

Математика

щейся в точке B 1 + , с концом B + е 1 1 . Составим у ^ из дуг [ B 10 B 1 + ],   [ B 10 B 1 ] = I [ B 10 B 1 ],

B ₁ ^- B ₂ ^- = I ( B ₁ ⁺ B ₂ ⁺ ) , а также из дуги границы Π ∪ I ( Π ) между точками B ₂ ⁺ и B ₂ ^- = I ( B ₂ ⁺ ) .

Множество У ^ ^ У ^ ^ У ^ является границей д U ^ области U ^ . Область U 0 является окрестностью полицикла Γ ₀ . Расстояние между Γ ₀ и ∂ U ₀ – положительная величина, которую обозначим ρ ₀ . Считая µ достаточно малым, будем иметь расстояние между ∂ U _µ и Γ ₀ большим ρ ₀ / 2 при всех µ ∈ ( - µ , µ ) . Но тогда U _µ – окрестность Γ ₀ .

Пусть U – ρ0 / 2 -окрестность Γ0 . Она содержится в Uµ, µ∈ (-µ,µ) . При µ∈ (-µ, 0] все положительные полутраектории, начинающиеся в Uµ , отличные от седла S(µ) , ω-предельны к Oµ и потому в U нет периодических траекторий векторных полей Xµ , µ∈ (-µ, 0] . Поскольку lt Γ+ = Γ0+ , то можно считать, что при выбранном µ Γ± ⊂ U для µ∈ (0,µ) . Других периоди-µ→0+ µ                                             µ ческих траекторий в Uµ , а потому и в U нет.

• 4.    Случай (Б). Как и в случае (А) векторное поле X _µ ^L , µ ∈ (0, µ ₁) имеет грубый устойчивый узел O _µ с координатами x = ξ ( µ ) >  0 , y = 0 . Для d ∈ (0, δ ) определено множество

K_d ^µ : = {( x , y ) ∈ V _δ ( O ): - d ≤ x <ξ ( µ ), 0 ≤ y ≤ξ ( µ ) - x } .

Поскольку diag( λ ₁( µ ), λ ₂( µ )) – матрица линейной части поля в точке O _µ , а по условию (Б)

λ (0) λ ⁰

• ²    = ² >  1 , то, выбрав достаточно малые µ ∈ (0, µ ] и d , можно считать, что при µ ∈ (0, µ )

λ 1 (0)    λ ₁ ⁰

P(x, y,µ) >0 для (x, y)∈ Kdµ, Q(x, y,µ) /P(x, y,µ) < -1 для (x, y)∈ Kdµ, y=ξ(µ)-x. (16) Рассмотрим в Kdµ дифференциальное уравнение y′ = R(x, y,µ) , где R(x, y,µ):= Q(x, y,µ) /P(x, y,µ) .

Ввиду (16) оно имеет решение Y ( x , u , µ ) , - d ≤ x < ξ ( µ ) , удовлетворяющее начальному условию Y ( - d , u , µ ) = v . Вследствие (1) Y ( - d ,0, µ ) ≡ 0 . Дуга y = Y ( x , u , µ ) , - d ≤ x ≤ 0 – пересечение с K_d ^µ траектории поля X _µ ^L . Поэтому ϕ ( ⋅ , µ ) : = Y (0, ⋅ , µ ) является функцией соответствия по траекториям векторных полей X _µ ^L и X _µ между дугами l _- ^µ : = {( x , y ) ∈ K_d ^µ : x = - d } и l ₀ ^µ : = {( x , y ) ∈ K_d ^µ : x = 0, 0 ≤ y ≤ξ ( µ )} .

Ввиду (3) найдутся числа α _L и α _R такие, что

1 <  ^a L < ^ 20 / А ⁰<  ^a R , а > a R (1 - У о ) .                          (17)

Аналогично лемме из [5] доказывается, что µ ₂ и d можно считать столь малыми, что для всех - d ≤ x ≤ 0 , µ ∈ (0, µ ₂ ) .

ϕ ( u , µ ) ≥ [ ξ ( µ )] ^{α R} ,[ ξ ( µ )] ^{α R} ≤ ϕ u ′ ( u , µ ) ≤ [ ξ ( µ )] ^{α L} .           (18)

Как и в случае (А) при достаточно малом µ ₃ ∈ (0, µ ₂ ] поле X _µ ^kS , µ ∈ ( - µ ₃ , µ ₃ ) , имеет грубое седло S ( µ ) с характеристическими показателями λ ₁ ^S ( µ ) >  0 и λ ₂ ^S ( µ ) <  0 , C^{r - 1} -гладко зависящими от µ .

Поскольку сепаратриса L ⁺ ₀ входит в точку O по направлению оси x , то число d можно считать выбранным так, что L ⁺ ₀ пересекает дугу l _- ⁰ в ее внутренней точке. Так как L ⁺ ₀ не содержит особых точек, то числа ε >  0 и µ ₄ ∈ (0, µ ₃ ] можно выбрать так, что траектория поля X _µ ,

Ройтенберг В.Ш.                        О бифуркациях некоторых сепаратрисных контуров кусочно-гладкой динамической системы с симметрией µ∈ (0, µ4) , начинающаяся в точке дуги l0µ с координатой y = v ∈ (0,ξ(µ)] пересекает дугу l-µ в точке с координатой x =ψ(v, µ) , где ψ удовлетворяет условиям (11) и (12).

Для любого µ∈ (0, µ4) определена функция последования f (⋅,µ) :=ϕ(ψ(⋅,µ),µ) и функция расхождения d(v,µ) := f (v,µ) - v , производная которой dv′(v,µ)=ϕu′(ψ(v,µ),µ)ψv′(v,µ)-1.                             (19)

Из (11) получаем

ψ _v ′ ( v , µ ) = v ^У ( µ ) - 1 г ( µ ) c ( µ ) + ρ _v ′ ( v , µ ) .                            (20)

По условию (Б) У (0) = У ₀ ≠ 1 . Если У (0) >  1 , то из (20) и (12) следует, что µ ₄ можно считать столь малым, что 0 < ψ _v ′ ( v , µ ) ≤ 1 для всех µ ∈ (0, µ ₄ ) , v ∈ (0, ξ ( µ )] . Отсюда, из (18), (4) и (19) получаем, что при некотором µ ∈ (0, µ ₄ ] d_v ′ ( v , µ ) <  0 для всех µ ∈ (0, µ ) , v ∈ (0, ξ ( µ )] . Поскольку d (0, µ ) >  0 , d ( ξ ( µ ), µ ) <  0 , то d ( ⋅ , µ ) имеет единственный нуль v ₀ ( µ ) ∈ (0, ξ ( µ )) . Соответственно, дугу l ₀ ^µ пересекает единственная периодическая траектория Γ _µ ⁺ ; она устойчивая и гиперболическая.

В случае У(0) < 1 , выбрав µ4 достаточно малым, при µ∈ (0,µ4) будем иметь 0 < 1 - У (µ) < 1 1            αL и v∗(µ) := (2c(0))1-7(µ)[ξ(µ)]1-7(µ) ∈ (0, ξ(µ)) . Из (17)–(20) получаем, что при некотором µ∈ (0, µ4]

α _L

d ( v , µ ) ≥ [ ξ ( µ )] ^{α R} - [ ξ ( µ )] ^{1 - У ( µ )} >  0 для всех v ∈ (0, v _∗ ( µ )] , µ ∈ (0, µ ) . d v ′ ( v , µ ) ≤ [ ξ ( µ )] ^αL 2 c (0) У (0)( v ∗ ( µ )) 7 ( µ ) - 1 _{- 1 ≤} У (0) - 1 <  0 для всех v ∈ [ v _∗ ( µ ), ξ ( µ )) , µ ∈ (0, µ ) . Из этих неравенств следует, что d ( ⋅ , µ ) имеет единственный нуль v ₀ ( µ ) ; он принадлежит интервалу ( v _∗ ( µ ), ξ ( µ )) и d_v ′ ( v ₀ ( µ ), µ ) <  0 . Тем самым, дугу l ₀ ^µ пересекает единственная периодическая траектория Γ _µ ⁺ ; она устойчивая и гиперболическая.

Окрестность U выбирается так же, как и в случае (А).