О частотных характеристиках цифрового генератора на основе ДВ-осциллятора Ван-дер-Поля

В радиотехнике генератором Ван-дер-Поля называется схема, состоящая из колебательного контура, источника питания и звена нелинейной обратной связи, как правило, представленного вакуумным триодом. Уравнение движения этой системы в безразмерном виде имеет вид

X - ( X - x 2 ) X + x = 0,

странство конечно, то даже в режиме хаотических автоколебаний фазовая траектория будет

где X — единственный безразмерный управляющий параметр.

В работе [1] была предложена дискретно-временная модель генератора Ван-дер-Поля, име-

ющая вид

У [ n ] = X i y [ n - 1] + X 2 y [ n - 2] +

+ Y (1 - У ²[ n - 1])( У [ n - 1] - У [ n - 2]).

Она представляет собой итерационное уравнение с тремя управляющими параметрами: X 1 , X 2 , У - Каждое следующее состояние системы вычисляется из двух предыдущих. В этой системе присутствует хаотический режим. Область значений управляющих параметров, при которых наблюдаются хаотические колебания, была установлена в работе [2].

При программном моделировании дискретновременной системы (1) одной из главных проблем становится представление фазовых траекторий. Поскольку в памяти компьютера невозможно представить все множество действительных чисел, получаемая система будет обладать лишь конечным фазовым пространством. Так как система детерминирована, а фазовое про-

рано или поздно зацикливаться.

В реализованной программной модели было использовано представление действительных чисел в формате чисел с плавающей запятой двойной точности (стандарт IEEE744), так как большинство современных компьютерных систем оптимизировано для работы именно с таким представлением, что обеспечивает высокую скорость вычислений. Таким образом, каждое состояние системы представляется набором из 8 байт, что определяет максимальную скорость формирования бинарной последовательности – 64 бита за цикл.

На рис. 1, а представлена числовая последовательность, генерируемая программной моделью

при значениях управляющих параметров, соответствующих хаотическому режиму. Для оценки хаотичности полученной числовой последовательности использовался расчет автокорреляционной функции:

C ( m ) =

N

- m

N - m

X k=1

ZX       ZX y [ k ] y [ k + m ],

У [ k ] = У [ k ] - У , 1 ^N

У = N X У ^{[ n ]}.

n = 1

Ее график для полученной последовательности представлен на рис. 1, б . Быстрое убывание

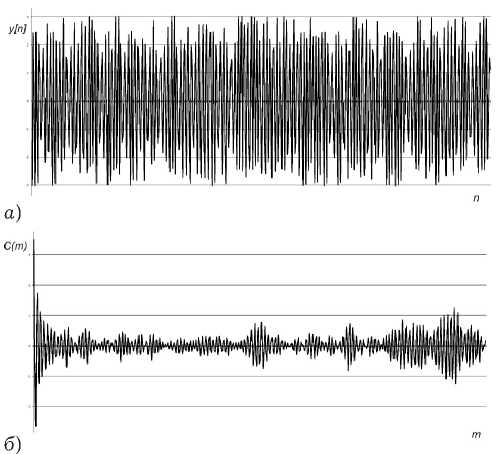
Рис. 1. Фазовая траектория дискретно-временной модели (1), полученная при параметрах: Х1 = 0.605, Х2 = - 0.958, у = 0.198, N = 500, и начальных условиях (0, 0.4) ( а ); функция автокорреляции (2) для данной траектории ( б )

и не периодичность функции автокорреляции свидетельствуют о хаотическом характере полученной числовой последовательности.

Однако, несмотря на хаотический характер получаемых числовых последовательностей, криптографические свойства бинарных последовательностей, получаемых простой записью внутреннего представления траектории, оказываются недостаточными для прохождения статистических тестов.

Знак |
(11 бит) Экспонента		(52 бита) Мантисса
	ТГГ	ТГГ	IIIIII	IIIIII	IIIIII	iiiiiiiiiiiiiiiiiiiiiii
63      56	55     48		47     40	39      32	31      24	23      16	15       8	7        0

Рис. 2. Представление чисел двойной точности по стандарту IEEE754

Представление чисел с плавающей запятой двойной точности в памяти компьютера показано на рис. 2. Биты пронумеруем от 0 слева направо. Таким образом бит 63 отражает знак числа: 0 – для положительного, 1 – для отрицательного, 52 бита (0–51) отведено под мантиссу и 11 бит (52–62) – под экспоненту (порядок).

Из графика траектории (рис. 1, а ) очевидно, что она ограничена по амплитуде, а следовательно, ее значения не будут значительно отличаться по порядку. Таким образом, малая вариативность 11 бит экспоненты снижает общие статистические характеристики результирующей бинарной последовательности. Аналогичный эффект могут оказывать также и подмножества бит мантиссы. На основании этого было принято решение использовать для формирования результирующей бинарной последовательности не все 64 бита внутреннего представления точек фазовой траектории, а лишь некоторое подмножество бит мантиссы. Таким образом, предпринимается попытка улучшения криптографических свойств бинарных последовательностей за

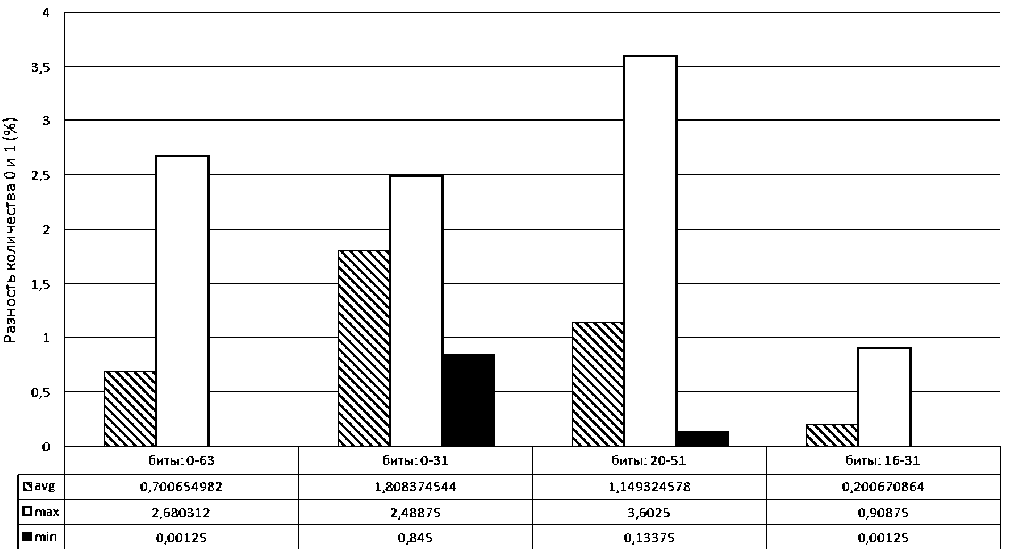
Рис. 3. Частотные характеристики бинарных последовательностей, полученных с использованием разных подмножеств двоичного представления IEEE754

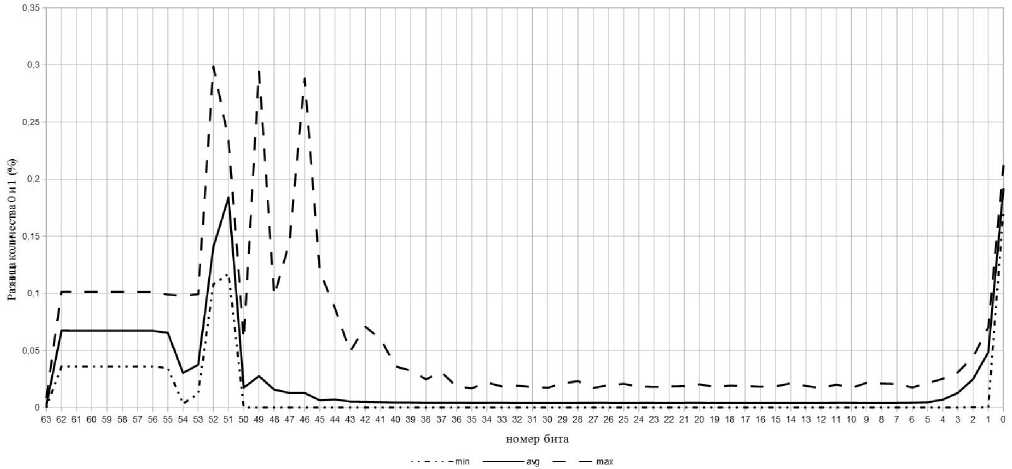
Рис. 4. Разница в количестве нулей и единиц для индивидуальных бит в представлении IEEE754

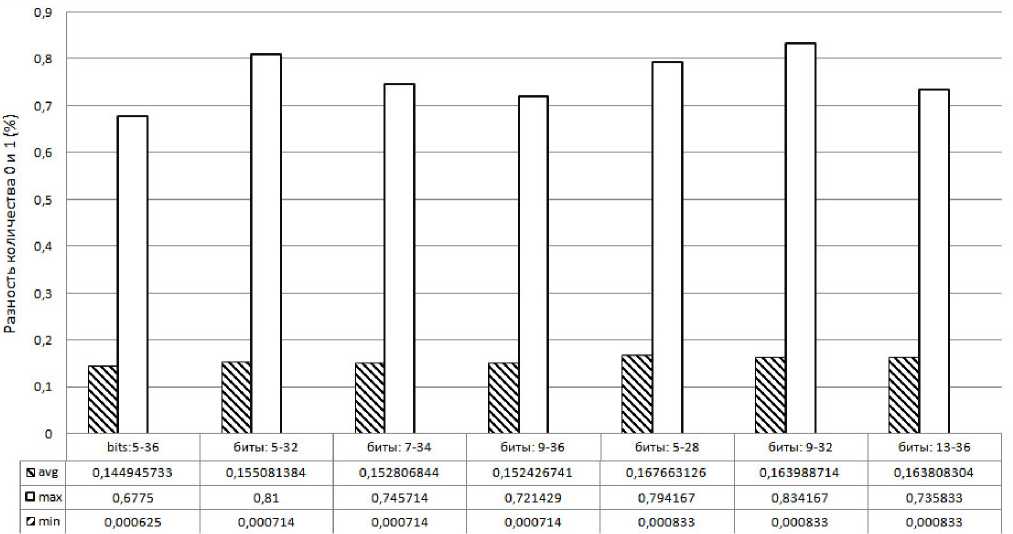
Рис. 5. Частотные характеристики бинарных последовательностей, полученных с использованием подмножеств двоичного представления IEEE754 в 32, 28 и 24 бита

счет снижения скорости генерации. Для выбора подмножества был проведен ряд экспериментов. Первоначально были рассмотрены подмножества в 32 бита, взятые от левой и правой границы мантиссы, а также подмножество в 16 бит из начала второй половины представления (биты 16–31).

Для исследования было рассмотрено 4000 последовательностей длиной в 10 000 циклов. В бинарных последовательностях было рассчитано процентное отношение модуля разности нулевых и единичных бит к длине последовательности.

В идеально случайной бинарной последовательности, где вероятности получения нуля или единицы в очередном бите равны, это отношение должно быть близким к 0. Результаты проведенного исследования представлены на рис. 3.

Минимальная разница в количестве нулей и единиц, а следовательно, и наилучшие частотные характеристики достигались при включении в результирующую бинарную последовательность подмножества в 16 бит с 16-го по 31-й. Однако использование такого подмножества существенно снижает скорость генерации последова-

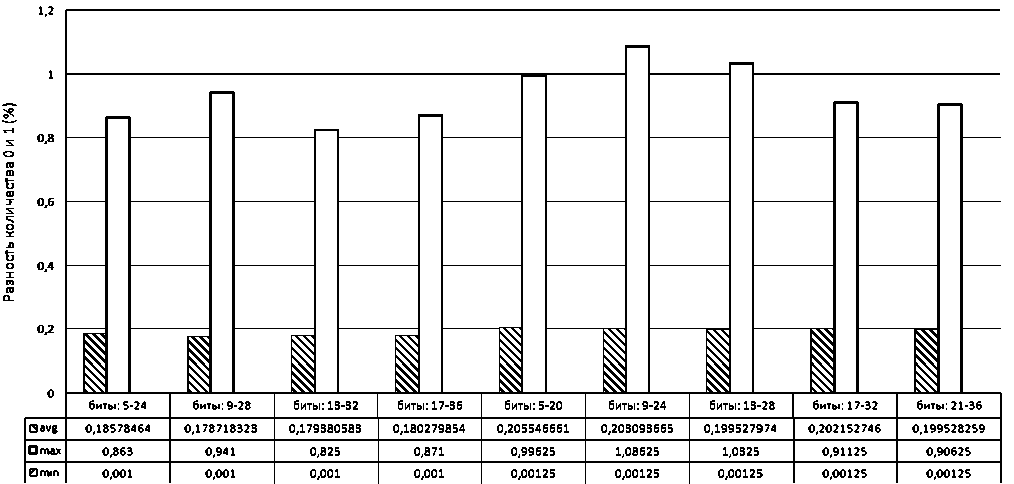
Рис. 6. Частотные характеристики бинарных последовательностей, полученных с использованием подмножеств двоичного представления IEEE754 в 20 и 16 бит

тельности – в 4 раза от максимально возможной. Также то, что результат при использовании бит 16–31 оказался лучше, чем при использовании бит 0–31, говорит о наличии подмножества мало меняющихся бит в промежутке с 0-го до 15-го бита.

С целью установления подмножеств бит мантиссы, негативно влияющих на частотные характеристики результирующих бинарных последовательностей, было проведено дополнительное исследование. За основу был взят тот же набор из 4000 последовательностей по 10 000 циклов, но частные характеристики теперь собирались не по подмножествам бит, а по каждому биту в отдельности. Результаты представлены на рис. 4. Они подтверждают предположение о низкой изменчивости бит экспоненты (52–62) и выделяют подмножество бит мантиссы, в котором также наблюдается значительная разница в количестве нулей и единиц. Оно состоит из 5 младших бит (0–4), а также 15 старших бит (37–51). Таким образом, исходя из частотных характеристик, предполагается достижение наилучших криптографических характеристик при включении в результирующую последовательность бит из промежутка с 5-го по 36-й.

Далее были исследованы частотные характеристики бинарных последовательностей, сформированных с использованием подмножеств выявленного промежутка. Были исследованы подмножества длиной 32, 28, 24, 20 и 16 бит. Результаты приведены на рис. 5 и 6. Наилучшие частотные характеристики были получены при использовании всего промежутка с 5-го по 36-й бит. При этом скорость генерации бинарной последовательности будет составлять половину от максимально возможной.

Однако криптографические свойства бинарных последовательностей зависят не только от их частотных характеристик. Поэтому для сравнения было использовано еще несколько статистических тестов из пакета NIST [3].

Сравнивалось 3 подхода: использование всех 64 бит представления, использование 32 бит (5–36) и использование 16 бит (16–31). С использованием каждого из идентичных параметров и начальных условий было произведено 500 бинарных последовательностей длиною по 1 миллиону бит. Все последовательности были о ценены следующим набором тестов: Frequency Test, Block Frequency Test, Runs Test, The Longest Run Of Ones Test, Discrete Fourier Transform Test, Approximate Entropy Test, Linear Complexity Test. В наборе статистических тестов NIST результатом прохождения каждого теста является значение p-value . Оно может принимать значения от 0 до 1, чем ближе значение к 1, тем лучшими характеристиками обладает исследуемая бинарная последовательность [3]. Результаты прохождения тестов представлены в таблице ниже.

Как и ожидалось, использование всех 64 бит представления IEEE754 приводит к низким результатам не только в частотном, но и в других тестах. Что касается использования подмно- жеств в 16 и 32 бита, то результаты прохождения тестов оказываются примерно одинаковыми. С одной стороны, некоторым тестам использование меньшего подмножества в 16 бит дает лучшие результаты, чем использование подмножества в 32 бита. Однако разница между их результатами невелика. С другой стороны, использование подмножества в 32 бита повышает скорость генерации бинарной последовательности в 2 раза.

Таким образом, при построении цифрового генератора на основе дискретно-временной модели осциллятора Ван-дер-Поля из соображений криптостойкости и производительности оказывается предпочтительным использовать представление действительных чисел по стандарту IEEE754 и включать в результирующую последовательность его подмножество с 5-го по 36-й бит.

Таблица

Тест Биты 0–63 Биты 16–31 Биты 5–36 Max p-value Avg p-value Min p-value Max p-value Avg p-value Min p-value Max p-value Avg p-value Min p-value Frequency 0,87768 0,01247 0,00000 0,99841 0,50175 0,00301 0,99681 0,45653 0,00018 Block Frequency 0,00000 0,00000 0,00000 0,99414 0,48273 0,00357 0,99638 0,47734 0,00123 Runs 0,00000 0,00000 0,00000 0,99450 0,49275 0,00015 0,99965 0,50943 0,00031 Longest Run 0,06864 0,00025 0,00000 0,99990 0,49152 0,00083 0,99802 0,50752 0,00085 Discrete Fourier Transform 0,00001 0,00000 0,00000 0,99415 0,48800 0,00298 0,99854 0,48294 0,00110 Approximate Entropy 0,00000 0,00000 0,00000 0,99496 0,48150 0,00154 0,99857 0,49643 0,00025 Linear Complexity 0,99957 0,49921 0,00161 0,99942 0,51126 0,00450 0,99560 0,51026 0,00183 дискретного осциллятора Ван-дер-Поля // Физика волновых процессов и радиотехнические системы. 2001. Т. 4. № 1. С. 18-21.